md_files/科研/高飞论文.md

# 高飞论文

## 网络重构分析

假设网络中有 $n$ 个节点，则矩阵 $A(G)$ 的维度为 $n \times n$，预测得到特征值和特征向量后，可以根据矩阵谱分解理论进行逆向重构网络邻接矩阵，表示如下：

$$
A(G) = \sum_{i=1}^n \hat{\lambda}_i \hat{x}_i \hat{x}_i^T
$$

其中 $\hat{\lambda}_i$ 和 $\hat{x}_i$ 分别为通过预测得到矩阵 $A(G)$ 的第 $i$ 个特征值和对应特征向量。  然而预测值和真实值之间存在误差，直接进行矩阵重构会使得重构误差较大。  对于这个问题，文献提出一种 0/1 矩阵近似恢复算法。
$$
a_{ij} = 
\begin{cases}
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
0, & \text{else}
\end{cases}
$$
只要我们的估计值与真实值之间差距**小于 0.5**，就能保证阈值处理以后准确地恢复原边信息。



文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律

真实矩阵 $A(G)$ 与预测矩阵 $\hat{A}(G) $ 之间的差为  
$$
A(G) - \hat{A}(G) = \sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
$$
对于任意元素 $(i, j)$ 上有  
$$
\left| \sum_{m=1}^n \Delta \lambda_m (\hat{x}_m \hat{x}_m^T)_{ij} \right| = |a_{ij} - \hat{a}_{ij}| < \frac{1}{2}
$$

于一个归一化的特征向量 $\hat{x}_m$，其外积矩阵 $\hat{x}_m \hat{x}_m^T$ 的元素理论上满足  
$$
|(\hat{x}_m \hat{x}_m^T)_{ij}| \leq 1.
$$
经过分析推导可以得出发生特征扰动时，网络精准重构条件为：
$$
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
$$

$$
\Delta {\lambda} < \frac{1}{2n}
$$

0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比，网络中节点数量越多，实现精准重构的要求也就越高。



如果在**高层次**（特征值滤波）的误差累积超过了一定阈值，就有可能在**低层次**（邻接矩阵元素）中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5，就可以保证0-1矩阵的精确重构。



## 基于时空特征的节点位置预测

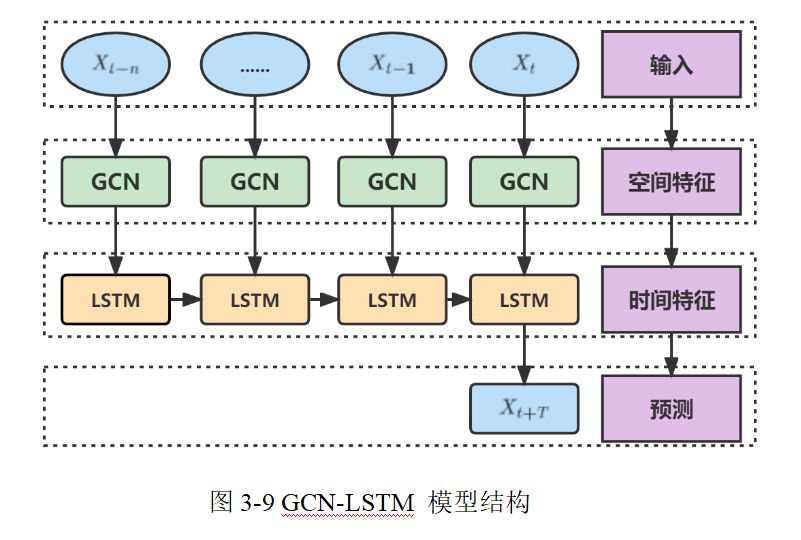
在本模型中，整个预测流程分为两大模块：

- **GCN 模块：主要用于从当前网络拓扑中提取每个节点的**空间表示**。这里的输入主要包括：
  - **邻接矩阵 $A$**：反映网络中节点之间的连通关系，维度为 $N \times N$，其中 $N$ 表示节点数。(可通过第二章网络重构的方式获取)
  - **特征矩阵 $H^{(0)}$**：一般是原始节点的属性信息，如历史位置数据，其维度为 $N \times d$，其中 $d$ 是初始特征维度。

- **LSTM 模块**：用于捕捉节点随时间变化的动态信息，对每个节点的历史运动轨迹进行序列建模，并预测未来时刻的坐标。  
  其输入通常是经过 GCN 模块处理后，每个节点在一段时间内获得的时空融合特征序列，维度一般为 $N \times T \times d'$，其中 $T$ 表示时间步数，$d'$ 是经过 GCN 后的特征维度。



### GCN 模块

#### 输入

- **邻接矩阵 $A$**：维度 $N \times N$。在实际操作中，通常先加上自环形成 
  $$
  \hat{A} = A + I.
  $$

- **特征矩阵 $H^{(0)}$**：维度 $N \times d$，每一行对应一个节点的初始特征（例如历史采样的位置信息或其他描述）。

#### 图卷积操作

常用的图卷积计算公式为：
$$
H^{(l+1)} = \sigma \Bigl(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} H^{(l)} W^{(l)} \Bigr)
$$
其中：

- $\tilde{A} = A + I$ 为加上自环后的邻接矩阵，
- $\tilde{D}$ 为 $\tilde{A}$ 的度矩阵，定义为 $\tilde{D}_{ii} = \sum_{j}\tilde{A}_{ij}$；
- $H^{(l)}$ 表示第 $l$ 层的节点特征，初始时 $H^{(0)}$ 就是输入特征矩阵；
- $W^{(l)}$ 是第 $l$ 层的权重矩阵，其维度通常为 $d_l \times d_{l+1}$（例如从 $d$ 到 $d'$）；
- $\sigma(\cdot)$ 是非线性激活函数，例如 ReLU 或 tanh。

经过一层或多层图卷积后，可以得到最终的节点表示矩阵 $H^{(L)}$（或记为 $X$），维度为 $N \times d'$。  
其中：

- 每一行 $x_i \in \mathbb{R}^{d'}$ 表示节点 $i$ 的空间特征，这些特征综合反映了其在网络拓扑中的位置及与邻居的关系。

#### 输出

- **GCN 输出**：形状为 $N \times d'$；若将模型用于时序建模，则对于每个时间步，都可以得到这样一个节点特征表示。
- 这里 $d'>d$ 。1.高维嵌入不仅保留了绝对位置信息，还包括了网络拓扑信息。2.兼容下游LSTM任务需求。



### LSTM 模块

#### 输入数据构造

在时序预测中，对于每个节点，我们通常有一段历史数据序列。假设我们采集了最近 $T$ 个时刻的数据，然后采用“滑动窗口”的方式，预测 $T+1$、 $T+2$...

- 对于每个时刻 $t$，节点 $i$ 的空间特征 $x_i^{(t)} \in \mathbb{R}^{d'}$ 由 GCN 得到；

- 将这些特征按照时间顺序排列，得到一个序列：
  $$
  X_i = \bigl[ x_i^{(t-T+1)},\, x_i^{(t-T+2)},\, \dots,\, x_i^{(t)} \bigr] \quad \in \mathbb{R}^{T \times d'}.
  $$

对于整个网络来说，可以将数据看作一个三维张量，维度为 $(N, T, d')$。

#### LSTM 内部运作

LSTM 通过内部门控机制（遗忘门 $f_t$、输入门 $i_t$ 和输出门 $o_t$）来更新其记忆状态 $C_t$ 和隐藏状态 $h_t$。公式如下

- **遗忘门**：
  $$
  f_t = \sigma(W_f [h_{t-1},\, x_t] + b_f)
  $$

- **输入门和候选记忆**：
  $$
  i_t = \sigma(W_i [h_{t-1},\, x_t] + b_i) \quad,\quad \tilde{C}_t = \tanh(W_C [h_{t-1},\, x_t] + b_C)
  $$

- **记忆更新**：
  $$
  C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t
  $$

- **输出门和隐藏状态**：
  $$
  o_t = \sigma(W_o [h_{t-1},\, x_t] + b_o), \quad h_t = o_t \odot \tanh(C_t)
  $$



其中，$x_t$ 在这里对应每个节点在时刻 $t$ 的 GCN 输出特征；  
$[h_{t-1},\, x_t]$ 为连接后的向量；  

LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$（其中 $d''$ 为 LSTM 的隐藏单元数）捕捉了时间上的依赖信息。

#### 输出与预测

最后，经过 LSTM 处理后，我们在最后一个时间步获得最终的隐藏状态 $h_t$ 或使用整个序列的输出；接着通过一个全连接层（FC层）将隐藏状态映射到最终的预测输出。

- **全连接层转换公式**：
  $$
  \hat{y}_i = W_{\text{fc}} \cdot h_t + b_{\text{fc}}
  $$

其中，假设预测的是二维坐标（例如 $x$ 和 $y$ 坐标），$W_{\text{fc}} \in \mathbb{R}^{2 \times d''}$，输出 $\hat{y}_i \in \mathbb{R}^2$ 表示节点 $i$ 在未来某个时刻（或下一时刻）的预测坐标。

![image-20250411142712730](https://pic.bitday.top/i/2025/04/11/nlpxlh-0.png)



若整个网络有 $N$ 个节点，则最终预测结果的输出维度为 $N \times 2$（或 $N \times T' \times 2$，如果预测多个未来时刻）。



### 疑问

该论文可能有点问题，每个节点只能预测自身未来位置，无法获取全局位置信息。如果先LSTM后GCN可能可以！