Commit on 2025/05/24 周六 21:15:55.43
This commit is contained in:
parent
bf6ae2a4e7
commit
0a4e20b6b8
122
科研/ZY网络重构分析.md
122
科研/ZY网络重构分析.md
@ -296,6 +296,56 @@ $$
|
||||
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### 对于归一化向量 $x_m$ 的研究
|
||||
|
||||
$$
|
||||
x_m = \begin{bmatrix} x_{m,1} \\ x_{m,2} \\ \vdots \\ x_{m,d} \end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
x_m x_m^T =
|
||||
\begin{bmatrix}
|
||||
x_{m,1}^2 & x_{m,1}x_{m,2} & \cdots & x_{m,1}x_{m,d} \\
|
||||
x_{m,2}x_{m,1} & x_{m,2}^2 & \cdots & x_{m,2}x_{m,d} \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
x_{m,d}x_{m,1} & x_{m,d}x_{m,2} & \cdots & x_{m,d}^2
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
(x_m x_m^T)_{ij}=x_{m,i}\,x_{m,j}\,,
|
||||
$$
|
||||
|
||||
**对于任意元素:**由于 $\|x_m\|_2=1$ 且 $|x_{m,i}|\le1$,必有
|
||||
$$
|
||||
|x_{m,i}x_{m,j}|\le1\,.
|
||||
$$
|
||||
|
||||
**对于非对角线元素:**
|
||||
|
||||
对任意 $i\neq j$,由
|
||||
$$
|
||||
x_{m,i}^2 + x_{m,j}^2 \le \sum_{k=1}^d x_{m,k}^2 = 1
|
||||
$$
|
||||
|
||||
$$
|
||||
(|x_{m,i}| - |x_{m,j}|)^2 \geq 0 \implies |x_{m,i}|^2 + |x_{m,j}|^2 \geq 2 |x_{m,i}| |x_{m,j}|.
|
||||
$$
|
||||
|
||||
$$
|
||||
|x_{m,i}x_{m,j}| = |x_{m,i}||x_{m,j}| \leq \frac{|x_{m,i}|^2 + |x_{m,j}|^2}{2} = \frac{x_{m,i}^2 + x_{m,j}^2}{2}.
|
||||
$$
|
||||
|
||||
$$
|
||||
|(x_m x_m^T)_{ij}|=|x_{m,i}x_{m,j}| \le \frac{x_{m,i}^2 + x_{m,j}^2}{2} \le \frac12\,,
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
#### 带权重构需控制两类误差:
|
||||
|
||||
这里暂时忽略特征向量的扰动,即 $x_m=\widetilde x_m$
|
||||
@ -345,9 +395,9 @@ $$
|
||||
$$
|
||||
\text{元素误差绝对值:}|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m| \cdot |(x_m x_m^T)_{ij}|
|
||||
$$
|
||||
由于 $|(x_m x_m^T)_{ij}| \leq 1$(归一化特征向量):
|
||||
对于非对角线元素,由于 $|(x_m x_m^T)_{ij}| \leq \frac12$(归一化特征向量):
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|
|
||||
|(A - A_\kappa)_{ij}| \leq \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)
|
||||
$$
|
||||
|
||||
- 研究整个矩阵误差:
|
||||
@ -373,7 +423,7 @@ $$
|
||||
$$
|
||||
|
||||
$$
|
||||
\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\leq 量化阈值\tau
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
|
||||
@ -417,83 +467,83 @@ $$
|
||||
#### 维数选择推导
|
||||
|
||||
$$
|
||||
\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\leq 量化阈值\tau
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
已知 $\sum_{m=1}^r |\Delta \lambda_m|=\eta$ ,量化阈值 $\tau$ ,令 $s=\tau-\eta$ ,设截断谱分解误差为 $\epsilon$
|
||||
已知 $\sum_{m=1}^r |\Delta \lambda_m|=\eta$ ,量化阈值 $\tau$ ,令 $s=2\tau-\eta$ ,设截断谱分解误差为 $\epsilon$
|
||||
$$
|
||||
\epsilon \leq \tau-\eta
|
||||
\epsilon \leq 2\tau-\eta
|
||||
$$
|
||||
借助**前缀和+二分查找**寻找最小的 $\kappa$ :
|
||||
|
||||
1. **预处理:计算前缀和**
|
||||
设已经有绝对值降序的估计特征值列表
|
||||
$$
|
||||
a_m = \bigl|\widetilde\lambda_m\bigr|,\quad m=1,\dots,r,
|
||||
$$
|
||||
并算出它们的前缀和
|
||||
$$
|
||||
S_k = \sum_{m=1}^k a_m,\quad k=0,1,\dots,r,
|
||||
\quad S_0=0.
|
||||
$$
|
||||
同时总和 $S_r = \sum_{m=1}^r a_m$ 就是当 $\kappa=0$ 时的尾部累积(最大截断误差)。
|
||||
|
||||
2. **将「尾和 ≤ 预算 $s$」转成前缀和条件**
|
||||
记预算 $s = \tau - \eta$,尾部累积
|
||||
2. 设绝对值降序的估计特征值列表为 $\bigl|\widetilde\lambda_1\bigr| \ge \bigl|\widetilde\lambda_2\bigr| \ge \cdots \ge \bigl|\widetilde\lambda_r\bigr|$,
|
||||
计算它们的前缀和:
|
||||
$$
|
||||
T(k) = \sum_{m=k+1}^r a_m = S_r - S_k.
|
||||
S_k = \sum_{m=1}^k \bigl|\widetilde\lambda_m\bigr|, \quad k=0,1,\dots,r, \quad S_0=0.
|
||||
$$
|
||||
要 $T(k)\le s$,等价于
|
||||
总和 $S_r = \sum_{m=1}^r \bigl|\widetilde\lambda_m\bigr|$ 对应 $\kappa=0$ 时的最大截断误差。
|
||||
|
||||
3. **将「尾和 ≤ 预算 $s$」转成前缀和条件**
|
||||
记预算 $s = 2\tau - \eta$,尾部累积(截断误差)为:
|
||||
$$
|
||||
S_k \;\ge\; S_r - s.
|
||||
T(k) = \sum_{m=k+1}^r \bigl|\widetilde\lambda_m\bigr| = S_r - S_k.
|
||||
$$
|
||||
令阈值
|
||||
条件 $T(k) \le s$ 等价于:
|
||||
$$
|
||||
S_k \ge S_r - s.
|
||||
$$
|
||||
定义阈值:
|
||||
$$
|
||||
\theta = S_r - s.
|
||||
$$
|
||||
|
||||
3. **二分查找最小 $\kappa$**
|
||||
4. **二分查找最小 $\kappa$**
|
||||
在已排好序的数组 $S_k$(严格单调递增或非减)中,用二分查找找出最小的 $k$ 使得
|
||||
$$
|
||||
S_k \;\ge\;\theta.
|
||||
$$
|
||||
这个 $k$ 就是最小满足 $T(k)\le s$ 的截断秩 $\kappa$。
|
||||
此 $k$ 即为所求的最小截断秩 $\kappa$。
|
||||
|
||||
**伪代码:**
|
||||
|
||||
```python
|
||||
# 输入:绝对值降序的列表 a[1..r], 预算 s ≥ 0
|
||||
S = [0] * (r+1)
|
||||
# 输入:绝对值降序的估计特征值列表 |λ̃₁| ≥ |λ̃₂| ≥ ... ≥ |λ̃ᵣ|, 预算 s ≥ 0
|
||||
S = [0] * (r+1) # 前缀和数组初始化
|
||||
for k in range(1, r+1):
|
||||
S[k] = S[k-1] + a[k] # 前缀和
|
||||
S[k] = S[k-1] + |λ̃ₖ| # 计算前缀和(实际代码中需替换 |λ̃ₖ| 为具体变量)
|
||||
|
||||
theta = S[r] - s # 查找阈值
|
||||
# 在 S[0..r] 中二分找最小 k 使 S[k] >= theta
|
||||
θ = S[r] - s # 计算查找阈值
|
||||
|
||||
# 在 S[0..r] 中二分查找最小 k 使得 S[k] ≥ θ
|
||||
low, high = 0, r
|
||||
while low < high:
|
||||
mid = (low + high) // 2
|
||||
if S[mid] < theta:
|
||||
if S[mid] < θ:
|
||||
low = mid + 1
|
||||
else:
|
||||
high = mid
|
||||
kappa = low
|
||||
κ = low # 最终得到的最小截断
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
奇异值分解
|
||||
|
||||
量化误差
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
滤波误差:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
高飞、李镇和都是**实验统计**误差加和获取 + 幂律分布和线性分布 精度预估??
|
||||
|
||||
|
||||
|
||||
|
||||
591
科研/草稿.md
591
科研/草稿.md
@ -1,70 +1,545 @@
|
||||
### **研究整个矩阵的误差(全局误差分析)**
|
||||
如何确定kmeans的簇数?节点之间的流量,空间转为时间的图。
|
||||
|
||||
为了分析整个矩阵的重构误差 $A - A_\kappa$,我们可以采用不同的矩阵范数来衡量误差的大小。常见的选择包括:
|
||||
压缩感知 函数拟合 采样定理 傅里叶变换
|
||||
|
||||
1. **Frobenius 范数(F-范数)**:衡量矩阵所有元素的平方和,适用于整体误差分析。
|
||||
2. **谱范数(2-范数)**:衡量矩阵的最大奇异值,适用于最坏情况下的误差分析。
|
||||
3. **核范数(Trace 范数)**:衡量矩阵的奇异值之和,适用于低秩矩阵分析。
|
||||
|
||||
|
||||
## **谱分解**与网络重构
|
||||
|
||||
实对称矩阵性质:
|
||||
|
||||
对于任意 $n \times n$ 的实对称矩阵 $A$:
|
||||
|
||||
1. **秩可以小于 $n$**(即存在零特征值,矩阵不可逆)。
|
||||
|
||||
2. 但仍然有 $n$ 个线性无关的特征向量(即可对角化)。
|
||||
|
||||
3. 特征值有正有负!!!
|
||||
|
||||
|
||||
|
||||
一个实对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的**对称矩阵** $A$,
|
||||
|
||||
**完整谱分解**可以表示为:
|
||||
$$
|
||||
A = Q \Lambda Q^T \\
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
$Q$是$n \times n$的正交矩阵,每一列是一个特征向量;$\Lambda$是$n \times n$的对角矩阵,对角线元素是特征值$\lambda_i$ ,其余为0。
|
||||
|
||||
其中,$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值,$x_i$ 是对应的特征向量。**(注意!这里的特征向量需要归一化!!!)**
|
||||
|
||||
|
||||
|
||||
**如果矩阵 $A$ 的秩为 $r$ ,那么谱分解里恰好有 $r$ 个非零特征值。**
|
||||
|
||||
用这 $r$ 对特征值/特征向量就能**精确**重构出 $A$,因为零特征值对矩阵重构不提供任何贡献。
|
||||
|
||||
因此,需要先对所有特征值取绝对值,从大到小排序,取前 $r$ 个!!!
|
||||
|
||||
|
||||
|
||||
**截断的谱分解**(取前 $\kappa$ 个特征值和特征向量)
|
||||
|
||||
如果我们只保留前 $\kappa$ 个绝对值最大的特征值和对应的特征向量,那么:
|
||||
|
||||
- **特征向量矩阵 $U_\kappa$**:取 $U$ 的前 $\kappa$ 列,维度为 $n \times \kappa$。
|
||||
- **特征值矩阵 $\Lambda_\kappa$**:取 $\Lambda$ 的前 $\kappa \times \kappa$ 子矩阵(即前 $\kappa$ 个对角线元素),维度为 $\kappa \times \kappa$。
|
||||
|
||||
因此,截断后的近似分解为:
|
||||
|
||||
$$
|
||||
A \approx U_\kappa \Lambda_\kappa U_\kappa^T\\
|
||||
A \approx \sum_{i=1}^{\kappa} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
**推导过程**
|
||||
|
||||
1. **特征值和特征向量的定义**
|
||||
对于一个对称矩阵 $A$,其特征值和特征向量满足:
|
||||
|
||||
$$
|
||||
A x_i = \lambda_i x_i
|
||||
$$
|
||||
|
||||
其中,$\lambda_i$ 是特征值,$x_i$ 是对应的特征向量。
|
||||
|
||||
2. **谱分解**
|
||||
将这些特征向量组成一个正交矩阵 $Q$
|
||||
|
||||
$A = Q \Lambda Q^T$
|
||||
|
||||
$$
|
||||
Q = \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix},
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix}.
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda Q^T = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_n^T \end{bmatrix}.
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda Q^T = \lambda_1 x_1 x_1^T + \lambda_2 x_2 x_2^T + \cdots + \lambda_n x_n x_n^T.
|
||||
$$
|
||||
|
||||
可以写为
|
||||
$$
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
3. **网络重构**
|
||||
在随机网络中,网络的邻接矩阵 $A$ 通常是对称的。利用预测算法得到的谱参数 $\{\lambda_i, x_i\}$ 后,就可以用以下公式重构网络矩阵:
|
||||
|
||||
$$
|
||||
A(G) = \sum_{i=1}^{n} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
|
||||
|
||||
| **性质** | **特征分解/谱分解** | **奇异值分解(SVD)** |
|
||||
| ------------ | -------------------------------- | ------------------------------------------ |
|
||||
| **适用矩阵** | 仅限**方阵**($n \times n$) | **任意矩阵**($m \times n$,包括矩形矩阵) |
|
||||
| **分解形式** | $A = P \Lambda P^{-1}$ | $A = U \Sigma V^*$ |
|
||||
| **矩阵类型** | 可对角化矩阵(如对称、正规矩阵) | 所有矩阵(包括不可对角化的方阵和非方阵) |
|
||||
| **输出性质** | 特征值($\lambda_i$)可能是复数 | 奇异值($\sigma_i$)始终为非负实数 |
|
||||
| **正交性** | 仅当 $A$ 正规时 $P$ 是酉矩阵 | $U$ 和 $V$ 始终是酉矩阵(正交) |
|
||||
|
||||
谱分解的对象为实对称矩阵,
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 网络重构分析
|
||||
|
||||
### 基于扰动理论的特征向量估算方法
|
||||
|
||||
设原矩阵为 $A$,扰动后矩阵为 $A+\zeta C$(扰动矩阵 $\zeta C$,$\zeta$是小参数),令其第 $i$ 个特征值、特征向量分别为 $\lambda_i,x_i$ 和 $\tilde\lambda_i,\tilde x_i$。
|
||||
|
||||
**特征向量的一阶扰动公式:**
|
||||
$$
|
||||
\Delta x_i
|
||||
=\tilde x_i - x_i
|
||||
\;\approx\;
|
||||
\zeta \sum_{k\neq i}
|
||||
\frac{x_k^T\,C\,x_i}{\lambda_i - \lambda_k}\;x_k,
|
||||
$$
|
||||
|
||||
- **输出**:对应第 $i$ 个特征向量修正量 $\Delta x_i$。
|
||||
|
||||
|
||||
|
||||
**特征值的一阶扰动公式:**
|
||||
$$
|
||||
\Delta\lambda_i = \tilde\lambda_i - \lambda_i \;\approx\;\zeta\,x_i^T\,C\,x_i
|
||||
$$
|
||||
**关键假设:**当扰动较小( $\zeta\ll1$) 且各模态近似正交均匀时,常作进一步近似
|
||||
$$
|
||||
x_k^T\,C\,x_i \;\approx\; x_i^T\,C\,x_i \;
|
||||
$$
|
||||
正交: $\{x_k\}$ 本身是正交基,这是任何对称矩阵特征向量天然具有的属性。
|
||||
|
||||
均匀:我们把 $C$ 看作“**不偏向任何特定模态**”的随机小扰动——换句话说,投影到任何两个方向 $(x_i,x_k)$ 上的耦合强度 $x_k^T\,C\,x_i\quad\text{和}\quad x_i^T\,C\,x_i$ 在数值量级上应当差不多,因此可以互相近似。
|
||||
|
||||
|
||||
|
||||
因此,将所有的 $x_k^T C x_i$ 替换为 $x_i^T C x_i$:
|
||||
$$
|
||||
\Delta x_i \approx \zeta \sum_{k\neq i} \frac{x_i^T C x_i}{\lambda_i - \lambda_k} x_k = \zeta (x_i^T C x_i) \sum_{k\neq i} \frac{1}{\lambda_i - \lambda_k} x_k = \sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
|
||||
$$
|
||||
|
||||
$$
|
||||
\Delta x_i \approx\sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
|
||||
$$
|
||||
|
||||
问题:
|
||||
|
||||
1. **当前时刻的邻接矩阵**
|
||||
$$
|
||||
A^{(1)}\in\mathbb R^{n\times n},\qquad
|
||||
A^{(1)}\,x_i^{(1)}=\lambda_i^{(1)}\,x_i^{(1)},\quad \|x_i^{(1)}\|=1.
|
||||
$$
|
||||
|
||||
2. **下一时刻的邻接矩阵**
|
||||
$$
|
||||
A^{(2)}\in\mathbb R^{n\times n},
|
||||
$$
|
||||
**已知**它的第 $i$ 个特征值 $\lambda_i^{(2)}$(卡尔曼滤波得来). **求**当前时刻的特征向量 $x_i^{(2)}$。
|
||||
|
||||
|
||||
|
||||
**下一时刻**第 $i$ 个特征向量的预测为
|
||||
$$
|
||||
\boxed{
|
||||
x_i^{(2)}
|
||||
\;=\;
|
||||
x_i^{(1)}+\Delta x_i
|
||||
\;\approx\;
|
||||
x_i^{(1)}
|
||||
+\sum_{k\neq i}
|
||||
\frac{\lambda_i^{(2)}-\lambda_i^{(1)}}
|
||||
{\lambda_i^{(1)}-\lambda_k^{(1)}}\;
|
||||
x_k^{(1)}.
|
||||
}
|
||||
$$
|
||||
通过该估算方法可以依次求出下一时刻的所有特征向量。
|
||||
|
||||
### 矩阵符号说明
|
||||
|
||||
- 原始(真实)邻接矩阵 $A$ ,假设 $A$ 的秩为 $r$: $\lambda_{r+1}=\cdots=\lambda_n=0$
|
||||
$$
|
||||
A = \sum_{m=1}^n \lambda_m\,x_m x_m^T=\begin{align*}
|
||||
\sum_{m=1}^r \lambda_m x_m x_m^T + \sum_{m=r+1}^n \lambda_m x_m x_m^T = \sum_{m=1}^r \lambda_m x_m x_m^T
|
||||
\end{align*},
|
||||
$$
|
||||
|
||||
|
||||
|
||||
- 滤波估计得到的矩阵及谱分解:
|
||||
$$
|
||||
\widetilde A = \sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||||
\quad \widetilde\lambda_1\ge\cdots\ge\widetilde\lambda_n\;
|
||||
$$
|
||||
|
||||
- 只取前 $\kappa$ 项重构 :
|
||||
$$
|
||||
A_\kappa \;=\;\sum_{m=1}^\kappa \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||||
$$
|
||||
|
||||
- 对 $A_\kappa$ 进行K-means聚类,得到 $A_{final}$
|
||||
|
||||
|
||||
|
||||
目标是让 $A_{final}$ = $A$
|
||||
|
||||
|
||||
|
||||
### **0/1矩阵**
|
||||
|
||||
其中 $\widetilde{\lambda}_i$ 和 $\widetilde{x}_i$ 分别为通过预测得到矩阵 $\widetilde A$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差,直接进行矩阵重构会使得重构误差较大。 对于这个问题,文献提出一种 0/1 矩阵近似恢复算法。
|
||||
$$
|
||||
a_{ij} =
|
||||
\begin{cases}
|
||||
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
|
||||
0, & \text{else}
|
||||
\end{cases}
|
||||
$$
|
||||
只要我们的估计值与真实值之间差距**小于 0.5**,就能保证阈值处理以后准确地恢复原边信息。
|
||||
|
||||
|
||||
|
||||
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
|
||||
|
||||
真实矩阵 $A$ 与预测矩阵 $\widetilde{A} $ 之间的差为 (秩为 $r$)
|
||||
$$
|
||||
A - \widetilde{A}=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T
|
||||
$$
|
||||
**若假设特征向量扰动可忽略,即$\widetilde x_m\approx x_m$ ,扰动可简化为(这里可能有问题,特征向量的扰动也要计算)**
|
||||
$$
|
||||
A - \widetilde{A} = \sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
对于任意元素 $(i, j)$ 上有
|
||||
$$
|
||||
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^r \Delta \lambda_m ({x}_m {x}_m^T)_{ij} \right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
于一个归一化的特征向量 ${x}_m$,其外积矩阵$ {x}_m {x}_m^T$ 满足
|
||||
$$
|
||||
|({x}_m {x}_m^T)_{ij}| \leq 1.
|
||||
$$
|
||||
例:
|
||||
$$
|
||||
x_m = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\\
|
||||
x_m x_m^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
||||
$$
|
||||
每个元素的绝对值$\leq1$
|
||||
|
||||
|
||||
$$
|
||||
\left| \sum_{m=1}^r \Delta \lambda_m (x_m x_m^T)_{ij} \right| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m|.
|
||||
$$
|
||||
为了确保 $|a_{ij} - \widetilde{a}_{ij}| < \frac{1}{2}$ 对所有 $(i,j)$ 成立,网络精准重构条件为:
|
||||
$$
|
||||
\sum_{m=1}^r\left| \Delta \lambda_m\right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
||||
|
||||
|
||||
|
||||
如果在**高层次**(特征值滤波)的误差累积超过了一定阈值,就有可能在**低层次**(邻接矩阵元素)中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5,就可以保证0-1矩阵的精确重构。
|
||||
|
||||
|
||||
|
||||
### **非0/1矩阵**
|
||||
|
||||
#### **量化误差**
|
||||
|
||||
对估计矩阵 $\tilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类,得到每个簇中心 $\{c_k\}_{k=1}^K$。
|
||||
|
||||
- **簇内平均偏差**:
|
||||
对于第 $k$簇,算该簇所有点到中心的平均绝对偏差:
|
||||
$$
|
||||
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
|
||||
$$
|
||||
|
||||
- **全局允许误差**:
|
||||
$$
|
||||
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### 对于归一化向量 $x_m$ 的研究
|
||||
|
||||
$$
|
||||
x_m = \begin{bmatrix} x_{m,1} \\ x_{m,2} \\ \vdots \\ x_{m,d} \end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
x_m x_m^T =
|
||||
\begin{bmatrix}
|
||||
x_{m,1}^2 & x_{m,1}x_{m,2} & \cdots & x_{m,1}x_{m,d} \\
|
||||
x_{m,2}x_{m,1} & x_{m,2}^2 & \cdots & x_{m,2}x_{m,d} \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
x_{m,d}x_{m,1} & x_{m,d}x_{m,2} & \cdots & x_{m,d}^2
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
(x_m x_m^T)_{ij}=x_{m,i}\,x_{m,j}\,,
|
||||
$$
|
||||
|
||||
**对于任意元素:**由于 $\|x_m\|_2=1$ 且 $|x_{m,i}|\le1$,必有
|
||||
$$
|
||||
|x_{m,i}x_{m,j}|\le1\,.
|
||||
$$
|
||||
|
||||
**对于非对角线元素:**
|
||||
|
||||
对任意 $i\neq j$,由
|
||||
$$
|
||||
x_{m,i}^2 + x_{m,j}^2 \le \sum_{k=1}^d x_{m,k}^2 = 1
|
||||
$$
|
||||
|
||||
$$
|
||||
(|x_{m,i}| - |x_{m,j}|)^2 \geq 0 \implies |x_{m,i}|^2 + |x_{m,j}|^2 \geq 2 |x_{m,i}| |x_{m,j}|.
|
||||
$$
|
||||
|
||||
$$
|
||||
|x_{m,i}x_{m,j}| = |x_{m,i}||x_{m,j}| \leq \frac{|x_{m,i}|^2 + |x_{m,j}|^2}{2} = \frac{x_{m,i}^2 + x_{m,j}^2}{2}.
|
||||
$$
|
||||
|
||||
$$
|
||||
|(x_m x_m^T)_{ij}|=|x_{m,i}x_{m,j}| \le \frac{x_{m,i}^2 + x_{m,j}^2}{2} \le \frac12\,,
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
#### 带权重构需控制两类误差:
|
||||
|
||||
这里暂时忽略特征向量的扰动,即 $x_m=\widetilde x_m$
|
||||
|
||||
1. **滤波误差**$\eta$:
|
||||
|
||||
**来源**:滤波器在谱域对真实特征值/向量的估计偏差,包括
|
||||
|
||||
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
|
||||
- **特征向量:矩阵扰动得来**
|
||||
- 设矩阵 $A$ 的秩为 $r$
|
||||
|
||||
$$
|
||||
A - \widetilde A=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
|
||||
$$
|
||||
\Bigl\|\sum_{m=1}^r \Delta\lambda_m\, x_m x_m^T\Bigr\|_F = \sqrt{\sum_{m=1}^r (\Delta\lambda_m)^2}.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
2. **截断谱分解误差** $\epsilon$:
|
||||
只取前 $\kappa$ 个特征对重构
|
||||
|
||||
$$
|
||||
A_\kappa \;=\;\sum_{m=1}^\kappa \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\;\sum_{m=1}^\kappa \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
$$
|
||||
\widetilde A - A_\kappa=\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
|
||||
$$
|
||||
\Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.\epsilon
|
||||
= \Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
3. **总的误差**
|
||||
$$
|
||||
\text{误差矩阵: } A - A_\kappa = \left( A - \widetilde{A} \right) + \left( \widetilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
|
||||
- 研究单个元素误差:
|
||||
$$
|
||||
\text{元素误差绝对值:}|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m| \cdot |(x_m x_m^T)_{ij}|
|
||||
$$
|
||||
对于非对角线元素,由于 $|(x_m x_m^T)_{ij}| \leq \frac12$(归一化特征向量):
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)
|
||||
$$
|
||||
|
||||
- 研究整个矩阵误差:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \left\| \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \right\|_F^2
|
||||
$$
|
||||
而 $\| x_m x_m^T \|_F = \sqrt{\text{tr}(x_m x_m^T x_m x_m^T)} = \sqrt{\text{tr}(x_m x_m^T)} = \| x_m \|_2 = 1$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2
|
||||
$$
|
||||
最终:
|
||||
$$
|
||||
\| A - A_\kappa \|_F = \sqrt{ \sum_{m=1}^r |\Delta \lambda_m|^2 + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|^2 }
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### **1. Frobenius 范数(F-范数)分析**
|
||||
F-范数定义为:
|
||||
$$
|
||||
\| A - A_\kappa \|_F = \sqrt{\sum_{i,j} |(A - A_\kappa)_{ij}|^2}
|
||||
$$
|
||||
由于我们已经知道:
|
||||
$$
|
||||
A - A_\kappa = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
我们可以计算其 F-范数:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \left\| \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \right\|_F^2
|
||||
$$
|
||||
由于 $x_m$ 是正交归一化的(假设 $x_i^T x_j = \delta_{ij}$),交叉项消失:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 \| x_m x_m^T \|_F^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2 \| x_m x_m^T \|_F^2
|
||||
$$
|
||||
而 $\| x_m x_m^T \|_F = \sqrt{\text{tr}(x_m x_m^T x_m x_m^T)} = \sqrt{\text{tr}(x_m x_m^T)} = \| x_m \|_2 = 1$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2
|
||||
$$
|
||||
最终:
|
||||
$$
|
||||
\| A - A_\kappa \|_F \leq \sqrt{ \sum_{m=1}^r |\Delta \lambda_m|^2 + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|^2 }
|
||||
$$
|
||||
**结论**:
|
||||
- F-范数误差由特征值偏差和截断特征值的平方和决定。
|
||||
- 如果 $\Delta \lambda_m$ 和 $\widetilde{\lambda}_m$ 较小,F-范数误差也会较小。
|
||||
4. **最终约束条件**:
|
||||
|
||||
---
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
### **2. 谱范数(2-范数)分析**
|
||||
谱范数定义为:
|
||||
$$
|
||||
\| A - A_\kappa \|_2 = \sigma_{\max}(A - A_\kappa)
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
$$
|
||||
其中 $\sigma_{\max}$ 是最大奇异值。由于 $A - A_\kappa$ 是对称矩阵,其谱范数等于最大绝对特征值:
|
||||
$$
|
||||
\| A - A_\kappa \|_2 = \max \left\{ |\Delta \lambda_1|, \dots, |\Delta \lambda_r|, |\widetilde{\lambda}_{\kappa+1}|, \dots, |\widetilde{\lambda}_r| \right\}
|
||||
$$
|
||||
**结论**:
|
||||
- 谱范数误差由最大的特征值偏差或截断特征值决定。
|
||||
- 如果所有 $\Delta \lambda_m$ 和 $\widetilde{\lambda}_m$ 都较小,谱范数误差也会较小。
|
||||
|
||||
---
|
||||
|
||||
### **3. 核范数(Trace 范数)分析**
|
||||
核范数定义为:
|
||||
$$
|
||||
\| A - A_\kappa \|_* = \sum_{i=1}^r \sigma_i (A - A_\kappa)
|
||||
$$
|
||||
由于 $A - A_\kappa$ 的奇异值就是 $|\Delta \lambda_1|, \dots, |\Delta \lambda_r|, |\widetilde{\lambda}_{\kappa+1}|, \dots, |\widetilde{\lambda}_r|$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_* = \sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|
|
||||
$$
|
||||
**结论**:
|
||||
- 核范数误差等于特征值偏差和截断特征值的绝对值和。
|
||||
- 这与逐元素误差的界一致,但核范数衡量的是全局误差。
|
||||
|
||||
---
|
||||
#### 量化阈值推导
|
||||
|
||||
要保证重构矩阵 $A_\kappa$ 在每个位置上“落到”正确的某一 簇而不搞混,就必须让重构误差的最大绝对值严格小于任意两个相邻量化级别之间的半距(half‐spacing)。具体地:
|
||||
|
||||
1. **量化级别及间距定义**
|
||||
设原始矩阵元素只能取 $K$ 个离散值:
|
||||
$$
|
||||
v_1 < v_2 < \cdots < v_K,
|
||||
$$
|
||||
相邻级别间距为:
|
||||
$$
|
||||
d_m = v_{m+1} - v_m,\quad m=1,\dots,K-1.
|
||||
$$
|
||||
|
||||
2. **最小间距确定**
|
||||
计算所有相邻级别的最小间距:
|
||||
$$
|
||||
d_{\min} = \min_{1\le m\le K-1} d_m.
|
||||
$$
|
||||
|
||||
3. **通用误差阈值**
|
||||
为确保重构值不会"越界"到相邻级别,取阈值:
|
||||
$$
|
||||
\boxed{\tau = \frac{d_{\min}}{2}.}
|
||||
$$
|
||||
|
||||
**示例:**
|
||||
|
||||
1. 0-1矩阵,$a=0, b=1,K=2$,量化阈值为0.5。
|
||||
2. 量化级别 $\{0,\,0.3,\,0.7,\,1\}$ ,$K=4$ 时:
|
||||
- 相邻间距:$0.3, 0.4, 0.3$
|
||||
- $d_{\min}=0.3$,故 $\tau=0.15$
|
||||
|
||||
|
||||
|
||||
#### 维数选择推导
|
||||
|
||||
$$
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
已知 $\sum_{m=1}^r |\Delta \lambda_m|=\eta$ ,量化阈值 $\tau$ ,令 $s=2\tau-\eta$ ,设截断谱分解误差为 $\epsilon$
|
||||
$$
|
||||
\epsilon \leq 2\tau-\eta
|
||||
$$
|
||||
借助**前缀和+二分查找**寻找最小的 $\kappa$ :
|
||||
|
||||
1. **预处理:计算前缀和**
|
||||
|
||||
2. 设绝对值降序的估计特征值列表为 $\bigl|\widetilde\lambda_1\bigr| \ge \bigl|\widetilde\lambda_2\bigr| \ge \cdots \ge \bigl|\widetilde\lambda_r\bigr|$,
|
||||
计算它们的前缀和:
|
||||
$$
|
||||
S_k = \sum_{m=1}^k \bigl|\widetilde\lambda_m\bigr|, \quad k=0,1,\dots,r, \quad S_0=0.
|
||||
$$
|
||||
总和 $S_r = \sum_{m=1}^r \bigl|\widetilde\lambda_m\bigr|$ 对应 $\kappa=0$ 时的最大截断误差。
|
||||
|
||||
3. **将「尾和 ≤ 预算 $s$」转成前缀和条件**
|
||||
记预算 $s = 2\tau - \eta$,尾部累积(截断误差)为:
|
||||
$$
|
||||
T(k) = \sum_{m=k+1}^r \bigl|\widetilde\lambda_m\bigr| = S_r - S_k.
|
||||
$$
|
||||
条件 $T(k) \le s$ 等价于:
|
||||
$$
|
||||
S_k \ge S_r - s.
|
||||
$$
|
||||
定义阈值:
|
||||
$$
|
||||
\theta = S_r - s.
|
||||
$$
|
||||
|
||||
4. **二分查找最小 $\kappa$**
|
||||
在已排好序的数组 $S_k$(严格单调递增或非减)中,用二分查找找出最小的 $k$ 使得
|
||||
$$
|
||||
S_k \;\ge\;\theta.
|
||||
$$
|
||||
此 $k$ 即为所求的最小截断秩 $\kappa$。
|
||||
|
||||
**伪代码:**
|
||||
|
||||
```python
|
||||
# 输入:绝对值降序的估计特征值列表 |λ̃₁| ≥ |λ̃₂| ≥ ... ≥ |λ̃ᵣ|, 预算 s ≥ 0
|
||||
S = [0] * (r+1) # 前缀和数组初始化
|
||||
for k in range(1, r+1):
|
||||
S[k] = S[k-1] + |λ̃ₖ| # 计算前缀和(实际代码中需替换 |λ̃ₖ| 为具体变量)
|
||||
|
||||
θ = S[r] - s # 计算查找阈值
|
||||
|
||||
# 在 S[0..r] 中二分查找最小 k 使得 S[k] ≥ θ
|
||||
low, high = 0, r
|
||||
while low < high:
|
||||
mid = (low + high) // 2
|
||||
if S[mid] < θ:
|
||||
low = mid + 1
|
||||
else:
|
||||
high = mid
|
||||
κ = low # 最终得到的最小截断
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
奇异值分解
|
||||
|
||||
量化误差
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
滤波误差:
|
||||
|
||||
高飞、李镇和都是**实验统计**误差加和获取 + 幂律分布和线性分布 精度预估??
|
||||
154
科研/高飞论文.md
154
科研/高飞论文.md
@ -135,7 +135,7 @@ $$
|
||||
|
||||
|
||||
|
||||
### 证明剩余特征值平稳:
|
||||
### 证明剩余特征值平稳(大模型说不可取):
|
||||
|
||||
#### 1. 收缩操作(Deflation)的严格定义
|
||||
|
||||
@ -228,6 +228,158 @@ $$
|
||||
|
||||
|
||||
|
||||
## JB-test
|
||||
|
||||
**JB-test(Jarque-Bera test)** 是一种用于检验样本数据是否服从正态分布的统计假设检验方法。这个检验特别适用于判断数据的偏度(skewness)和峰度(kurtosis)是否符合正态分布的特性。
|
||||
|
||||
正态分布具有以下特性:
|
||||
|
||||
- **偏度(Skewness)** 为 $0$,表示数据的分布是对称的。
|
||||
- **峰度(Kurtosis)** 为 $3$,表示数据的峰度是"中等"的。
|
||||
|
||||
|
||||
|
||||
### JB-test的统计量
|
||||
|
||||
Jarque-Bera统计量的计算公式为:
|
||||
|
||||
$$
|
||||
JB = \frac{n}{6} \left( S^2 + \frac{(K - 3)^2}{4} \right)
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
- $n$ 是样本的大小。
|
||||
- $S$ 是样本的偏度(skewness),衡量分布的对称性。
|
||||
- $K$ 是样本的峰度(kurtosis),衡量分布的尖峭程度。
|
||||
|
||||
### JB-test的分布和检验步骤
|
||||
|
||||
- **零假设($H_0$)**:数据服从正态分布。
|
||||
- **备择假设($H_1$)**:数据不服从正态分布。
|
||||
|
||||
在进行检验时,首先计算 JB 统计量,然后将其与卡方分布进行比较:
|
||||
|
||||
- JB 统计量的分布近似于自由度为 $2$ 的卡方分布(当样本量较大时)。
|
||||
- 如果 JB 统计量的值大于临界值(根据设定的显著性水平,比如 $0.05$),则拒绝零假设,即认为数据不符合正态分布。
|
||||
- 如果 JB 统计量的值小于临界值,则无法拒绝零假设,即认为数据服从正态分布。
|
||||
|
||||
|
||||
|
||||
### 结论
|
||||
|
||||
- **如果 JB 统计量接近 $0$**,说明数据的偏度和峰度与正态分布的期望非常接近,数据可能符合正态分布。
|
||||
- **如果 JB 统计量远离 $0$**,则说明数据的偏度或峰度与正态分布的特征差异较大,数据不符合正态分布。
|
||||
|
||||
|
||||
|
||||
## 特征值精度预估
|
||||
|
||||
卡尔曼滤波的状态更新方程为 $x_k' = x_k + K (z_k - H x_k)$,如果增益系数 $K$ 变小,那么先验预测 $x_k$ 接近真实值;反之如果增益系数 $K$ 变大,则测量值 $z_k$ 更接近真实值。增益系数$K$受到过程噪声$Q$以及观测噪声$R$的影响,因此估算的过程噪声$Q$和观测噪声$R$,与实际值是否一致,将决定$K$是否准确,从而影响滤波的精度。
|
||||
|
||||
设过程噪声$Q$的期望为$\mu_q$,方差为$\sigma_q$;观测噪声$R$的期望为$\mu_r$,方差为$\sigma_r$。其中$\mu_q$、$\sigma_q$和$\mu_r$、$\sigma_r$时未知;$n_q$、$n_r$分别为过程噪声与观测噪声的采样长度。
|
||||
|
||||
针对我们研究对象,特征值滤波公式的系数都属于实数域。$P_{k-1}$是由上次迭代产生,因此可以$FP_{k-1}F^T$看作定值,则$P_k$的方差等于$Q$的方差,即:
|
||||
|
||||
$$
|
||||
\text{var}(P_k) = \text{var}(Q)
|
||||
$$
|
||||
|
||||
对卡尔曼增益$K$进行变换可得:
|
||||
|
||||
$$
|
||||
K = \frac{1}{H + (H^T)^{-1} \cdot \left(\frac{R}{P_k}\right)}
|
||||
$$
|
||||
|
||||
且方差满足:
|
||||
|
||||
$$
|
||||
D\left(\frac{R}{P_k}\right) = \frac{\sigma_r}{\sigma_q}
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
- $H$ 为观测矩阵
|
||||
- $(H^T)^{-1}$ 表示观测矩阵转置的逆
|
||||
- $\sigma_r$, $\sigma_q$ 分别为观测噪声和过程噪声的标准差
|
||||
|
||||
设$\{Q_1, Q_2, \cdots, Q_m\}$是属于$\{Q\}$的一组样本,$\{R_1, R_2, \cdots, R_n\}$是属于$\{R\}$的一组样本,由于过程噪声$Q$与观测噪声$R$都满足高斯分布则可知如下卡方分布:
|
||||
$$
|
||||
\sum_{i=1}^{n_q} \left( \frac{Q_i - \overline{Q}}{\sigma_q} \right)^2 \sim \chi^2(n_q - 1) \quad \text{(2-21)}
|
||||
$$
|
||||
|
||||
$$
|
||||
\sum_{i=1}^{n_r} \left( \frac{R_i - \overline{R}}{\sigma_r} \right)^2 \sim \chi^2(n_r - 1) \quad \text{(2-22)}
|
||||
$$
|
||||
|
||||
对两式作变形可得$F$分布:
|
||||
|
||||
$$
|
||||
\frac{\chi^{2}(n_{q})/(n_{q}-1)}{\chi^{2}(n_{r})/(n_{r}-1)} \sim F(n_{q}-1,n_{r}-1) \quad \text{(2-23)}
|
||||
$$
|
||||
|
||||
观测噪声$Q$和过程噪声$R$比值$\sigma_{r}/\sigma_{q}$的区间估计满足:
|
||||
|
||||
$$
|
||||
\frac{S_{q}^{*2}\sigma_{r}^{2}}{S_{r}^{*2}\sigma_{q}^{2}} \sim F(n_{q}-1,n_{r}-1)
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
$$
|
||||
S_{q}^{*2} = \frac{1}{n_{q}-1}\sum_{i=1}^{n_{q}}(Q_{i}-\overline{Q})^{2} \quad \text{(2-24)}
|
||||
$$
|
||||
|
||||
$$
|
||||
S_{r}^{*2} = \frac{1}{n_{r}-1}\sum_{i=1}^{n_{r}}(R_{i}-\overline{R})^{2} \quad \text{(2-25)}
|
||||
$$
|
||||
|
||||
对于置信度为$1-\alpha$的情况:
|
||||
$$
|
||||
P\left\{F_{1-\alpha/2}(n_q-1,n_r-1) \leq \frac{S_{q}^{*2}\sigma_{r}^{2}}{S_{r}^{*2}\sigma_{q}^{2}} \leq F_{\alpha/2}(n_q-1,n_r-1)\right\}=1-\alpha \quad \text{(2-26)}
|
||||
$$
|
||||
|
||||
于是可以得到:
|
||||
|
||||
$$
|
||||
P\left\{F_{1-\alpha/2}(n_q-1,n_r-1)\frac{S_{r}^{*2}}{S_{q}^{*2}} \leq \frac{\sigma_{r}^{2}}{\sigma_{q}^{2}} \leq F_{\alpha/2}(n_q-1,n_r-1)\frac{S_{r}^{*2}}{S_{q}^{*2}}\right\}=1-\alpha \quad \text{(2-27)}
|
||||
$$
|
||||
|
||||
|
||||
我们采用绝对误差来进行精度分析,设$\xi$为绝对误差上限,即:
|
||||
|
||||
$$
|
||||
\text{MSE}(\hat{x} - x) \leq \xi
|
||||
$$
|
||||
|
||||
则有:
|
||||
|
||||
$$
|
||||
\xi = \left( \frac{1}{c + m\theta_{min}} - \frac{1}{c + m\theta_{max}} \right) E\left( x_k' - x_k \right)
|
||||
$$
|
||||
|
||||
$$
|
||||
= \frac{m\left( \theta_{max} - \theta_{min} \right)}{(c + m\theta_{min}) \left( c + m\theta_{max} \right)} E\left( x_k' - x_k \right) \quad(2-28)
|
||||
$$
|
||||
|
||||
|
||||
|
||||
当$cm=1$时,可得:
|
||||
|
||||
$$
|
||||
= \frac{(\theta_{max} - \theta_{min}) E \left( x_k' - x_k \right)}{(c^2 + \theta_{min}) (c^2 + \theta_{max})}
|
||||
|
||||
\quad(2-29)
|
||||
$$
|
||||
|
||||
其中 $\theta_{min} = \left( F_{1-\alpha/2}(n_q - 1, n_r - 1) \frac{S_r^*}{S_q^*} \right)^{1/2}$,$\theta_{max} = \left( F_{\alpha/2}(n_q - 1, n_r - 1) \frac{S_r^*}{S_q^*} \right)^{1/2}$
|
||||
|
||||
|
||||
|
||||
根据上述推导,在获得预测模型的过程噪声与观测噪声后,可以根据区间估计的方法进行误差上界预估。
|
||||
|
||||
|
||||
|
||||
## 基于时空特征的节点位置预测
|
||||
|
||||
在本模型中,整个预测流程分为两大模块:
|
||||
|
||||
@ -869,12 +869,20 @@ build: ./web_app #两种写法是等效的
|
||||
docker-compose build
|
||||
```
|
||||
|
||||
**启动容器:**这个命令用于启动服务,参数 `-d` 表示以后台守护进程的方式运行。如果镜像不存在,它会自动构建镜像;但如果镜像已经存在,则默认直接使用现有的镜像启动容器。
|
||||
**启动容器:**
|
||||
|
||||
```shell
|
||||
docker-compose up -d
|
||||
```
|
||||
|
||||
- 如果之前没有容器,就新建一个。如果有,若对比现有容器中的配置和compose文件中的配置,若不一样则删除旧容器,用新的配置重新启动一个新容器。
|
||||
|
||||
- `-d` 参数让所有容器在后台运行
|
||||
|
||||
- 一般镜像不会重建,除非你修改了构建上下文(`build:` 下的 Dockerfile ),或者 加了`--build`参数
|
||||
|
||||
|
||||
|
||||
**进入容器:**
|
||||
|
||||
```shell
|
||||
@ -883,30 +891,14 @@ docker compose exec -it filebrowser sh
|
||||
|
||||
注意!一般进入数据卷挂载,直接在宿主机上操作容器内部就可以了!!!!!
|
||||
|
||||
**只针对 pyapp 服务进行重构和启动,不影响其他服务运行**
|
||||
|
||||
|
||||
**启动或更新指定服务**
|
||||
|
||||
镜像不存在或需重建时才构建,配置变动(或镜像变动)则重建容器,都没变则一动不动
|
||||
|
||||
```shell
|
||||
docker-compose build pyapp
|
||||
```
|
||||
|
||||
启动容器并进入bash
|
||||
|
||||
```shell
|
||||
docker compose run --rm -it pyapp /bin/bash
|
||||
```
|
||||
|
||||
运行脚本
|
||||
|
||||
```shell
|
||||
python typecho_markdown_upload/main.py
|
||||
```
|
||||
|
||||
|
||||
|
||||
**更新并重启容器**
|
||||
|
||||
```shell
|
||||
docker-compose up --build -d
|
||||
docker compose up -d pyapp
|
||||
```
|
||||
|
||||
|
||||
@ -927,24 +919,30 @@ docker-compose ps
|
||||
docker-compose logs flask_app --since 1h #只显示最近 1 小时
|
||||
```
|
||||
|
||||
**停止运行的容器**
|
||||
|
||||
只停止容器,容器还在磁盘上,`docker compose start`或`docker compose up`时容器会带着之前的状态继续运行
|
||||
|
||||
```shell
|
||||
docker-compose stop
|
||||
docker-compose stop flask_app #指定某个服务
|
||||
```
|
||||
|
||||
**停止并删除所有由 docker-compose 启动的容器、网络等(默认不影响挂载卷)。**
|
||||
|
||||
下次再 `up`,就得重新创建容器、网络,但镜像不受影响(除非你显式用 `--rmi` 删除镜像)。
|
||||
|
||||
```shell
|
||||
docker-compose down #不能单独指定
|
||||
```
|
||||
|
||||
**删除停止的容器**
|
||||
|
||||
```shell
|
||||
docker-compose rm
|
||||
docker-compose rm flask_app
|
||||
```
|
||||
|
||||
**停止运行的容器**
|
||||
默认不会删除网络、卷
|
||||
|
||||
```shell
|
||||
docker-compose stop
|
||||
docker-compose stop flask_app #指定某个服务
|
||||
docker-compose rm # 删除所有已停止的服务容器(会交互式询问要不要删除)
|
||||
docker-compose rm flask_app # 只删除指定服务的容器
|
||||
```
|
||||
|
||||
**启动服务**
|
||||
|
||||
@ -688,6 +688,46 @@ Component衍生注解
|
||||
|
||||
|
||||
|
||||
### 依赖注入
|
||||
|
||||
1.Autowird注入
|
||||
|
||||
```java
|
||||
@Autowired
|
||||
private PaymentClient paymentClient; // 字段直接加 @Autowired
|
||||
```
|
||||
|
||||
2.构造器注入(推荐)
|
||||
|
||||
1)手写构造器
|
||||
|
||||
```java
|
||||
public class OrderService {
|
||||
|
||||
private final PaymentClient paymentClient;
|
||||
|
||||
// 在构造器上无需加 @Autowired(Spring Boot 下可省略)
|
||||
public OrderService(PaymentClient paymentClient) {
|
||||
this.paymentClient = paymentClient;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
2)Lombok `@RequiredArgsConstructor`
|
||||
|
||||
用 Lombok 自动为所有 `final` 字段生成构造器,进一步简化写法:
|
||||
|
||||
```java
|
||||
@RequiredArgsConstructor
|
||||
public class OrderService {
|
||||
|
||||
private final PaymentClient paymentClient; // Lombok 会在编译期生成构造器
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 配置文件
|
||||
|
||||
#### 配置优先级
|
||||
@ -795,7 +835,7 @@ Spring提供的简化方式套路:
|
||||
|
||||
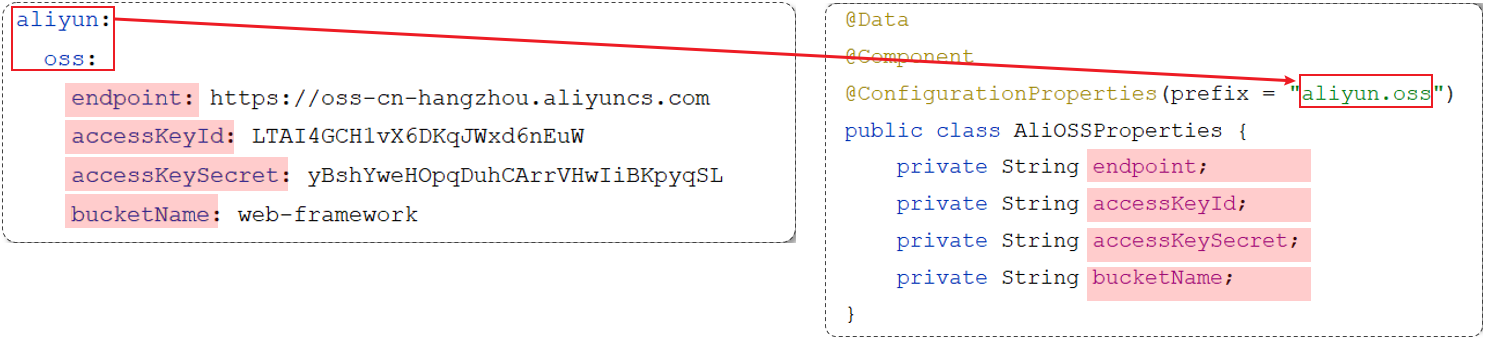
|
||||
|
||||
4. (可选)引入依赖pom.xml (自动生成配置元数据,让 IDE 能识别并补全你在 `application.properties/yml` 中的自定义配置项,提高开发体验)
|
||||
4. (可选)引入依赖pom.xml (自动生成配置元数据,让 IDE **能识别并补全**你在 `application.properties/yml` 中的自定义配置项,提高开发体验,不加不影响运行!)
|
||||
|
||||
```java
|
||||
<dependency>
|
||||
@ -1142,7 +1182,8 @@ public class SpringbootWebConfig2Application {
|
||||
}
|
||||
```
|
||||
|
||||
5. `@RequestParam`,如果方法的参数名与请求参数名不同,需要在 `@RequestParam` 注解中指定请求参数的名字。
|
||||
5. `@RequestParam`,
|
||||
1)如果方法的参数名与请求参数名不同,需要在 `@RequestParam` 注解中指定请求参数的名字。
|
||||
类似`@PathVariable`,可以指定参数名称。
|
||||
|
||||
```java
|
||||
@ -1155,7 +1196,7 @@ public class SpringbootWebConfig2Application {
|
||||
}
|
||||
```
|
||||
|
||||
还可以设置默认值
|
||||
2)还可以设置默认值
|
||||
|
||||
```java
|
||||
@RequestMapping("/greet")
|
||||
@ -1164,7 +1205,7 @@ public class SpringbootWebConfig2Application {
|
||||
}
|
||||
```
|
||||
|
||||
如果既改请求参数名字,又要设置默认值
|
||||
3)如果既改请求参数名字,又要设置默认值
|
||||
|
||||
```java
|
||||
@RequestMapping("/greet")
|
||||
@ -1173,6 +1214,12 @@ public class SpringbootWebConfig2Application {
|
||||
}
|
||||
```
|
||||
|
||||
4)如果方法参数是简单类型(`int`/`Integer`、`String`、`boolean`/`Boolean` 等及它们的一维数组),那么无需使用@RequestParam,**如果是Collection集合类型,必须使用**。
|
||||
|
||||
```java
|
||||
List<ItemDTO> queryItemByIds(@RequestParam("ids") Collection<Long> ids);
|
||||
```
|
||||
|
||||
|
||||
|
||||
5. 控制反转与依赖注入:
|
||||
|
||||
@ -91,6 +91,21 @@ int c = a & b; // 0001₂ = 1
|
||||
System.out.println(c); // 输出 1
|
||||
```
|
||||
|
||||
典型用途:
|
||||
|
||||
**清零低位**:`x & (~((1<<k)-1))` 清掉最低 `k` 位;
|
||||
|
||||
```shell
|
||||
(1<<3)-1 = 0000_0111
|
||||
~((1<<3)-1) = 1111_1000
|
||||
```
|
||||
|
||||
**判断奇偶**:`x & 1`,若结果是 `1` 说明奇数,若 `0` 说明偶数;
|
||||
|
||||
**掩码提取**:只保留想要的位置,其他位置置 `0`。
|
||||
|
||||
|
||||
|
||||
按位或 `|`: 只要两个对应位有一个为 1,结果位就为 1。
|
||||
|
||||
```java
|
||||
@ -100,6 +115,13 @@ int c = a | b; // 0111₂ = 7
|
||||
System.out.println(c); // 输出 7
|
||||
```
|
||||
|
||||
**典型用途**:
|
||||
|
||||
- **置位**:`x | (1<<k)` 把第 `k` 位置 `1`;
|
||||
- **合并标志**:将两个掩码或在一起。
|
||||
|
||||
|
||||
|
||||
按位异或 `^`: 两个对应位不同则为 1,相同则为 0。
|
||||
|
||||
```java
|
||||
@ -109,7 +131,7 @@ int c = a ^ b; // 0110₂ = 6
|
||||
System.out.println(c); // 输出 6
|
||||
```
|
||||
|
||||
左移 `<<`: 整体二进制左移 N 位,右侧补 0;相当于乘以 2ⁿ。
|
||||
算术左移 `<<`: 整体二进制左移 n 位,右侧补 0;相当于乘以 2ⁿ。(因为最高位可能走出符号位,结果符号可能翻转)
|
||||
|
||||
```java
|
||||
int a = 3; // 0011₂
|
||||
@ -117,6 +139,8 @@ int b = a << 2; // 1100₂ = 12
|
||||
System.out.println(b); // 输出 12
|
||||
```
|
||||
|
||||
逻辑(无符号)右移`>>>`:在**最高位**一律补 `0`,不管原符号位是什么。
|
||||
|
||||
|
||||
|
||||
### Random
|
||||
@ -253,7 +277,7 @@ public static List<String> splitBySpace(String s) {
|
||||
向字符串末尾追加内容。
|
||||
|
||||
2.**`insert(int offset, String str)`**
|
||||
在指定位置插入字符串。(有妙用,头插法可以实现倒序)`insert(0,str)`
|
||||
在指定位置插入字符串。(有妙用,**头插法**可以实现倒序)`insert(0,str)`
|
||||
|
||||
3.**`delete(int start, int end)`**
|
||||
删除从 `start` 到 `end` 索引之间的字符。
|
||||
@ -286,6 +310,10 @@ public static List<String> splitBySpace(String s) {
|
||||
|
||||
|
||||
|
||||
`StringBuffer` 插入int类型的数字时,会自动转为字符串插入。
|
||||
|
||||
|
||||
|
||||
### HashMap
|
||||
|
||||
- 基于哈希表实现,查找、插入和删除的平均时间复杂度为 O(1)。
|
||||
@ -534,14 +562,14 @@ public class PriorityQueueExample {
|
||||
|
||||
**自定义排序:按第二个元素的值构建小根堆**
|
||||
|
||||
如何比较器返回负数,则第一个数排在前面->优先级高->在堆顶
|
||||
如果比较器返回负数,则第一个数排在前面->优先级高->在堆顶
|
||||
|
||||
```java
|
||||
public class CustomPriorityQueue {
|
||||
public static void main(String[] args) {
|
||||
// 定义一个 PriorityQueue,其中每个元素是 int[],并且按照数组第二个元素升序排列
|
||||
PriorityQueue<int[]> minHeap = new PriorityQueue<>(
|
||||
(a, b) -> return a[i]-b[i];
|
||||
(a, b) -> a[1] - b[1]
|
||||
);
|
||||
|
||||
// 添加数组
|
||||
|
||||
790
自学/微服务.md
790
自学/微服务.md
@ -38,6 +38,8 @@
|
||||
- 优点:项目代码集中,管理和运维方便
|
||||
- 缺点:服务之间耦合,编译时间较长
|
||||
|
||||
,每个模块都要有:pom.xml application.yml controller service mapper pojo 启动类
|
||||
|
||||
|
||||
|
||||
IDEA配置小技巧:
|
||||
@ -47,3 +49,791 @@ IDEA配置小技巧:
|
||||
|
||||
|
||||
2.配置service窗口,以显示多个微服务启动类
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/21/pf7h7n-0.png" alt="image-20250521153717289" style="zoom: 80%;" />
|
||||
|
||||
3.如何在idea中虚拟多服务负载均衡?
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/21/tzm5xp-0.png" alt="image-20250521181337779" style="zoom:80%;" />
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/21/u0vvwe-0.png" alt="image-20250521181552335" style="zoom:80%;" />
|
||||
|
||||
More options->Add VM options -> **-Dserver.port=xxxx**
|
||||
|
||||
这边设置不同的端口号!
|
||||
|
||||
|
||||
|
||||
## 服务注册和发现
|
||||
|
||||
注册中心、服务提供者、服务消费者三者间关系如下:
|
||||
|
||||
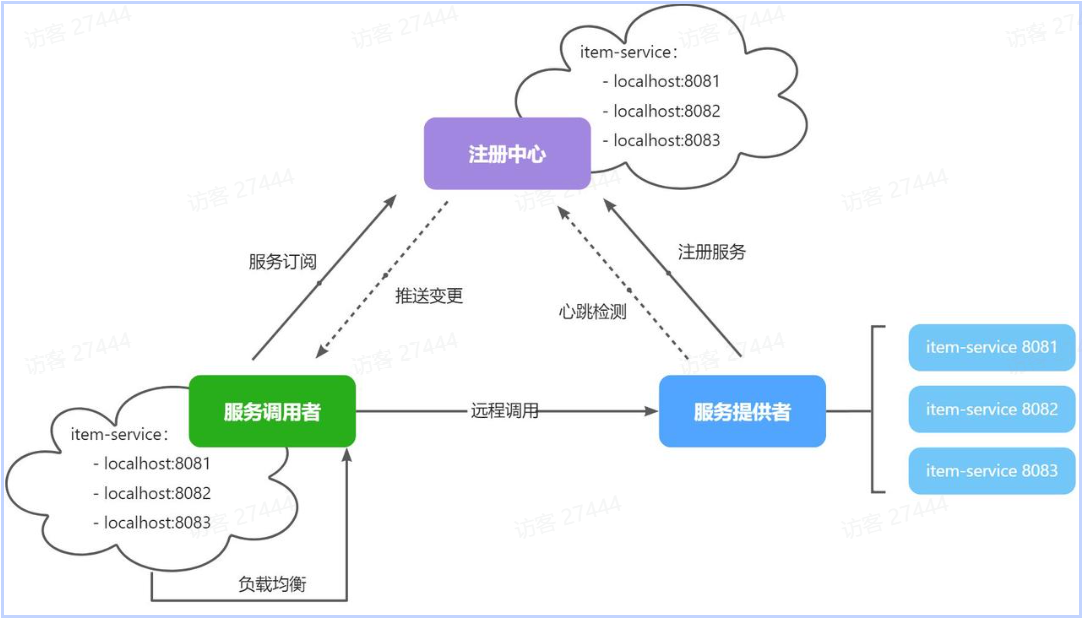
|
||||
|
||||
流程如下:
|
||||
|
||||
- 服务启动时就会**注册自己的服务信息**(服务名、IP、端口)到注册中心
|
||||
- 调用者可以从注册中心订阅想要的服务,获取服务对应的实例列表(1个服务可能多实例部署)
|
||||
- 调用者自己对实例列表**负载均衡,挑选一个实例**
|
||||
- 调用者向该实例发起远程调用
|
||||
|
||||
当服务提供者的实例宕机或者启动新实例时,调用者如何得知呢?
|
||||
|
||||
- 服务提供者会**定期**向注册中心发送请求,报告自己的健康状态(**心跳请求**)
|
||||
- 当注册中心长时间收不到提供者的心跳时,会认为该实例宕机,将其**从服务的实例列表中剔除**
|
||||
- 当服务有新实例启动时,会发送注册服务请求,其信息会被记录在注册中心的服务实例列表
|
||||
- 当注册中心服务列表变更时,会**主动通知微服务**,更新本地服务列表(防止服务调用者继续调用挂逼的服务)
|
||||
|
||||
### Nacos部署:
|
||||
|
||||
1.依赖mysql中的一个数据库 ,可由nacos.sql初始化
|
||||
|
||||
2.需要.env文件,配置和数据库的连接信息:
|
||||
|
||||
```text
|
||||
PREFER_HOST_MODE=hostname
|
||||
MODE=standalone
|
||||
SPRING_DATASOURCE_PLATFORM=mysql
|
||||
MYSQL_SERVICE_HOST=124.71.159.***
|
||||
MYSQL_SERVICE_DB_NAME=nacos
|
||||
MYSQL_SERVICE_PORT=3307
|
||||
MYSQL_SERVICE_USER=root
|
||||
MYSQL_SERVICE_PASSWORD=*******
|
||||
MYSQL_SERVICE_DB_PARAM=characterEncoding=utf8&connectTimeout=1000&socketTimeout=3000&autoReconnect=true&useSSL=false&allowPublicKeyRetrieval=true&serverTimezone=Asia/Shanghai
|
||||
```
|
||||
|
||||
3.docker部署:
|
||||
|
||||
```yml
|
||||
nacos:
|
||||
image: nacos/nacos-server:v2.1.0
|
||||
container_name: nacos-server
|
||||
restart: unless-stopped
|
||||
env_file:
|
||||
- ./nacos/custom.env # 自定义环境变量文件
|
||||
ports:
|
||||
- "8848:8848" # Nacos 控制台端口
|
||||
- "9848:9848" # RPC 通信端口 (TCP 长连接/心跳)
|
||||
- "9849:9849" # gRPC 通信端口
|
||||
networks:
|
||||
- hm-net
|
||||
depends_on:
|
||||
- mysql
|
||||
volumes:
|
||||
- ./nacos/init.d:/docker-entrypoint-init.d # 如果需要额外初始化脚本,可选
|
||||
```
|
||||
|
||||
启动完成后,访问地址:http://ip:8848/nacos/
|
||||
|
||||
初始账号密码都是nacos
|
||||
|
||||
|
||||
|
||||
### 服务注册
|
||||
|
||||
1.在`item-service`的`pom.xml`中添加依赖:
|
||||
|
||||
```xml
|
||||
<!--nacos 服务注册发现-->
|
||||
<dependency>
|
||||
<groupId>com.alibaba.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-alibaba-nacos-discovery</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2.配置Nacos
|
||||
|
||||
在`item-service`的`application.yml`中添加nacos地址配置:
|
||||
|
||||
```yml
|
||||
spring:
|
||||
application:
|
||||
name: item-service #服务名
|
||||
cloud:
|
||||
nacos:
|
||||
server-addr: 124.71.159.***:8848 # nacos地址
|
||||
```
|
||||
|
||||
注意,服务注册默认连9848端口!云服务需要开启该端口!
|
||||
|
||||

|
||||
|
||||
配置里的item-service就是服务名!
|
||||
|
||||
|
||||
|
||||
### 服务发现
|
||||
|
||||
前两步同服务注册
|
||||
|
||||
3.通过DiscoveryClient发现服务实例列表,然后通过负载均衡算法,选择一个实例去调用
|
||||
|
||||
discoveryClient发现服务 + restTemplate远程调用
|
||||
|
||||
```java
|
||||
@Service
|
||||
public class CartServiceImpl {
|
||||
|
||||
@Autowired
|
||||
private DiscoveryClient discoveryClient; // 注入 DiscoveryClient
|
||||
|
||||
@Autowired
|
||||
private RestTemplate restTemplate; // 用于发 HTTP 请求
|
||||
|
||||
private void handleCartItems(List<CartVO> vos) {
|
||||
// 1. 获取商品 id 列表
|
||||
Set<Long> itemIds = vos.stream()
|
||||
.map(CartVO::getItemId)
|
||||
.collect(Collectors.toSet());
|
||||
|
||||
// 2.1. 发现 item-service 服务的实例列表
|
||||
List<ServiceInstance> instances = discoveryClient.getInstances("item-service");
|
||||
|
||||
// 2.2. 负载均衡:随机挑选一个实例
|
||||
ServiceInstance instance = instances.get(
|
||||
RandomUtil.randomInt(instances.size())
|
||||
);
|
||||
|
||||
// 2.3. 发送请求,查询商品详情
|
||||
String url = instance.getUri().toString() + "/items?ids={ids}";
|
||||
ResponseEntity<List<ItemDTO>> response = restTemplate.exchange(
|
||||
url,
|
||||
HttpMethod.GET,
|
||||
null,
|
||||
new ParameterizedTypeReference<List<ItemDTO>>() {},
|
||||
String.join(",", itemIds)
|
||||
);
|
||||
|
||||
// 2.4. 处理结果
|
||||
if (response.getStatusCode().is2xxSuccessful()) {
|
||||
List<ItemDTO> items = response.getBody();
|
||||
// … 后续处理 …
|
||||
} else {
|
||||
throw new RuntimeException("查询商品失败: " + response.getStatusCode());
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### OpenFeign
|
||||
|
||||
让**远程调用像本地方法调用一样简单**
|
||||
|
||||
#### 快速入门
|
||||
|
||||
1.引入依赖
|
||||
|
||||
```xml
|
||||
<!--openFeign-->
|
||||
<dependency>
|
||||
<groupId>org.springframework.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-openfeign</artifactId>
|
||||
</dependency>
|
||||
<!--负载均衡器-->
|
||||
<dependency>
|
||||
<groupId>org.springframework.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-loadbalancer</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2.启用OpenFeign
|
||||
|
||||
在服务调用者`cart-service`的`CartApplication`启动类上添加注解:
|
||||
|
||||
`@EnableFeignClients`
|
||||
|
||||
3.编写OpenFeign客户端
|
||||
|
||||
在`cart-service`中,定义一个新的接口,编写Feign客户端:
|
||||
|
||||
```java
|
||||
@FeignClient("item-service")
|
||||
public interface ItemClient {
|
||||
|
||||
@GetMapping("/items")
|
||||
List<ItemDTO> queryItemByIds(@RequestParam("ids") Collection<Long> ids);
|
||||
}
|
||||
```
|
||||
|
||||
`queryItemByIds`这个方法名可以随便取,但`@GetMapping("/items")` 和 `@RequestParam("ids")` 要跟 item-service 服务中实际暴露的接口路径和参数名保持一致(直接参考服务提供者的Controller层对应方法对应即可);
|
||||
|
||||
一个客户端对应一个服务,可以在ItemClient里面写多个方法。
|
||||
|
||||
4.使用
|
||||
|
||||
```java
|
||||
List<ItemDTO> items = itemClient.queryItemByIds(Arrays.asList(1L, 2L, 3L));
|
||||
```
|
||||
|
||||
Feign 会帮你把 `ids=[1,2,3]` 序列化成一个 HTTP GET 请求,URL 形如:
|
||||
|
||||
```text
|
||||
GET http://item-service/items?ids=1&ids=2&ids=3
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 连接池
|
||||
|
||||
Feign底层发起http请求,依赖于其它的框架。其底层支持的http客户端实现包括:
|
||||
|
||||
- HttpURLConnection:默认实现,不支持连接池
|
||||
- Apache HttpClient :支持连接池
|
||||
- OKHttp:支持连接池
|
||||
|
||||
这里用带有连接池的HttpClient 替换默认的
|
||||
|
||||
1.引入依赖
|
||||
|
||||
```xml
|
||||
<dependency>
|
||||
<groupId>io.github.openfeign</groupId>
|
||||
<artifactId>feign-httpclient</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2.开启连接池
|
||||
|
||||
```yml
|
||||
feign:
|
||||
httpclient:
|
||||
enabled: true # 使用 Apache HttpClient(默认关闭)
|
||||
```
|
||||
|
||||
重启服务,连接池就生效了。
|
||||
|
||||
|
||||
|
||||
#### 最佳实践
|
||||
|
||||
如果拆分了交易微服务(`trade-service`),它也需要远程调用`item-service`中的根据id批量查询商品功能。这个需求与`cart-service`中是一样的。那么会再次定义`ItemClient`接口导致重复编程。
|
||||
|
||||
- 思路1:抽取到微服务之外的公共module,需要调用client就引用该module的坐标。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/22/jv1r9u-0.png" alt="image-20250522120106182" style="zoom:80%;" />
|
||||
|
||||
- 思路2:每个微服务自己抽取一个module,比如item-service,将需要共享的domain实体放在item-dto模块,需要供其他微服务调用的cilent放在item-api模块,自己维护自己的,然后其他微服务引入maven坐标直接使用。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/22/j5mb6l-0.png" alt="image-20250522115834339" style="zoom:80%;" />
|
||||
|
||||
大型项目思路2更清晰、更合理。但这里选择思路1,方便起见。
|
||||
|
||||
|
||||
|
||||
**拆分之后重启报错:**`Parameter 0 of constructor in com.hmall.cart.service.impl.CartServiceImpl required a bean of type 'com.hmall.api.client.ItemClient' that could not be found.`
|
||||
|
||||
是因为:Feign Client 没被扫描到,Spring Boot 默认只会在主应用类所在包及其子包里扫描 `@FeignClient`。
|
||||
|
||||
需要额外设置basePackages
|
||||
|
||||
```java
|
||||
package com.hmall.cart;
|
||||
@MapperScan("com.hmall.cart.mapper")
|
||||
@EnableFeignClients(basePackages= "com.hmall.api.client")
|
||||
@SpringBootApplication
|
||||
public class CartApplication {
|
||||
public static void main(String[] args) {
|
||||
|
||||
SpringApplication.run(CartApplication.class, args);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 网关
|
||||
|
||||
在微服务拆分后的联调过程中,经常会遇到以下问题:
|
||||
|
||||
- 不同业务数据分布在各自微服务,需要维护**多套地址和端口**,调用繁琐且易错;
|
||||
- 前端无法直接访问注册中心(如 Nacos),无法实时获取服务列表,导致接口切换不灵活。
|
||||
|
||||
此外,单体架构下只需完成一次**登录与身份校验**,所有业务模块即可共享用户信息;但在微服务架构中:
|
||||
|
||||
- 每个微服务是否都要重复实现登录校验和用户信息获取?
|
||||
- 服务间调用时,如何安全、可靠地传递用户身份?
|
||||
|
||||
通过引入 **API 网关**,我们可以在**统一入口处解决**以上问题:它提供动态路由与负载均衡,前端**只需调用一个地址**;它与注册中心集成,实时路由调整;它还在网关层集中完成登录鉴权和用户信息透传,下游服务无需重复实现安全逻辑。
|
||||
|
||||
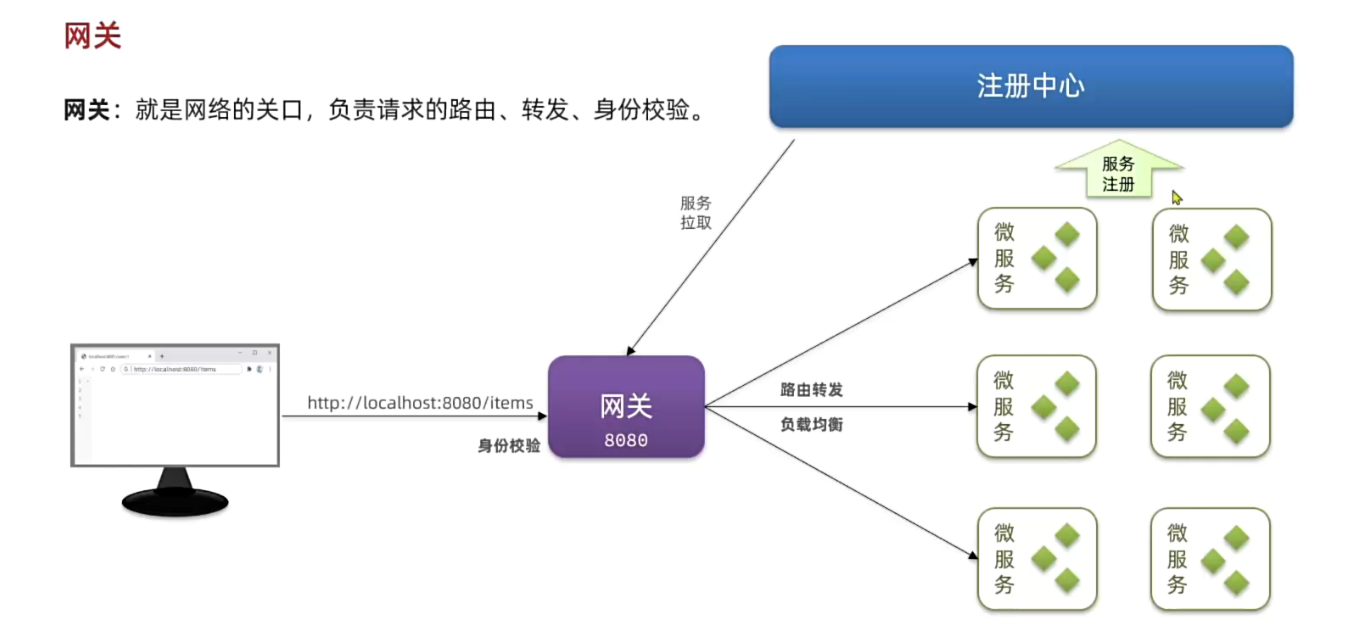
|
||||
|
||||
### 快速入门
|
||||
|
||||
网关本身也是一个独立的微服务,因此也需要创建一个模块开发功能。大概步骤如下:
|
||||
|
||||
- 创建网关微服务
|
||||
- 引入SpringCloudGateway、NacosDiscovery依赖
|
||||
- 编写启动类
|
||||
- 配置网关路由
|
||||
|
||||
1.依赖引入:
|
||||
|
||||
```xml
|
||||
<!-- 网关 -->
|
||||
<dependency>
|
||||
<groupId>org.springframework.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-gateway</artifactId>
|
||||
</dependency>
|
||||
|
||||
<!-- Nacos Discovery -->
|
||||
<dependency>
|
||||
<groupId>com.alibaba.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-alibaba-nacos-discovery</artifactId>
|
||||
</dependency>
|
||||
|
||||
<!-- 负载均衡 -->
|
||||
<dependency>
|
||||
<groupId>org.springframework.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-loadbalancer</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2.配置网关路由
|
||||
|
||||
**`id`**:给这条路由起个唯一的标识,方便你在日志、监控里看是哪个规则。(最好和服务名一致)
|
||||
|
||||
**`uri: lb://xxx`**:`xxx` 必须和服务注册时的名字一模一样(比如 `Item-service` 或全大写 `ITEM-SERVICE`,取决于你在微服务启动时 `spring.application.name` 配置)
|
||||
|
||||
```yml
|
||||
server:
|
||||
port: 8080
|
||||
spring:
|
||||
application:
|
||||
name: gateway
|
||||
cloud:
|
||||
nacos:
|
||||
server-addr: 192.168.150.101:8848
|
||||
gateway:
|
||||
routes:
|
||||
- id: item # 路由规则id,自定义,唯一
|
||||
uri: lb://item-service # 路由的目标服务,lb代表负载均衡,会从注册中心拉取服务列表
|
||||
predicates: # 路由断言,判断当前请求是否符合当前规则,符合则路由到目标服务
|
||||
- Path=/items/**,/search/** # 支持多个路径模式,用逗号隔开
|
||||
- id: cart
|
||||
uri: lb://cart-service
|
||||
predicates:
|
||||
- Path=/carts/**
|
||||
- id: user
|
||||
uri: lb://user-service
|
||||
predicates:
|
||||
- Path=/users/**,/addresses/**
|
||||
- id: trade
|
||||
uri: lb://trade-service
|
||||
predicates:
|
||||
- Path=/orders/**
|
||||
- id: pay
|
||||
uri: lb://pay-service
|
||||
predicates:
|
||||
- Path=/pay-orders/**
|
||||
|
||||
```
|
||||
|
||||
`predicates`:路由断言,其实就是匹配条件
|
||||
|
||||
| After | 是某个时间点后的请求 | - After=2037-01-20T17:42:47.789-07:00[America/Denver] |
|
||||
| ------ | ------------------------ | ----------------------------------------------------- |
|
||||
| Before | 是某个时间点之前的请求 | - Before=2031-04-13T15:14:47.433+08:00[Asia/Shanghai] |
|
||||
| Path | 请求路径必须符合指定规则 | - Path=/red/{segment},/blue/** |
|
||||
|
||||
|
||||
|
||||
**Ant风格路径**
|
||||
|
||||
用来灵活地匹配文件或请求路径:
|
||||
|
||||
`?`:匹配单个字符(除了 `/`)。
|
||||
|
||||
- 例如,`/user/??/profile` 能匹配 `/user/ab/profile`,但不能匹配 `/user/a/profile` 或 `/user/abc/profile`。
|
||||
|
||||
`*`:匹配任意数量的字符(零 个或 多个),但不跨越路径分隔符 `/`。
|
||||
|
||||
- 例如,`/images/*.png` 能匹配 `/images/a.png`、`/images/logo.png`,却不匹配 `/images/icons/logo.png`。
|
||||
|
||||
`**`:匹配任意层级的路径(可以跨越多个 `/`)。
|
||||
|
||||
- 例如,`/static/**` 能匹配 `/static/`、`/static/css/style.css`、`/static/js/lib/foo.js`,甚至 `/static/a/b/c/d`。
|
||||
|
||||
`AntPathMatcher` 是 Spring Framework 提供的一个工具类,用来对“Ant 风格”路径模式做匹配
|
||||
|
||||
```java
|
||||
@Component
|
||||
@ConfigurationProperties(prefix = "auth")
|
||||
public class AuthProperties {
|
||||
private List<String> excludePaths;
|
||||
// getter + setter
|
||||
}
|
||||
|
||||
@Component
|
||||
public class AuthInterceptor implements HandlerInterceptor {
|
||||
private final AntPathMatcher pathMatcher = new AntPathMatcher();
|
||||
private final List<String> exclude;
|
||||
|
||||
public AuthInterceptor(AuthProperties props) {
|
||||
this.exclude = props.getExcludePaths();
|
||||
}
|
||||
|
||||
@Override
|
||||
public boolean preHandle(HttpServletRequest req,
|
||||
HttpServletResponse res,
|
||||
Object handler) {
|
||||
String path = req.getRequestURI(); // e.g. "/search/books/123"
|
||||
|
||||
// 检查是否匹配任何一个“放行”模式
|
||||
for (String pattern : exclude) {
|
||||
if (pathMatcher.match(pattern, path)) {
|
||||
return true; // 放行,不做 auth
|
||||
}
|
||||
}
|
||||
|
||||
// 否则执行认证逻辑
|
||||
// ...
|
||||
return false;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
当然
|
||||
|
||||
```yaml
|
||||
predicates:
|
||||
- Path=/users/**,/addresses/**
|
||||
```
|
||||
|
||||
这里不需要手写JAVA逻辑进行路径匹配,因为Gateway自动实现了。但是后面自定义Gateway过滤器的时候就需要`AntPathMatcher`了!
|
||||
|
||||
|
||||
|
||||
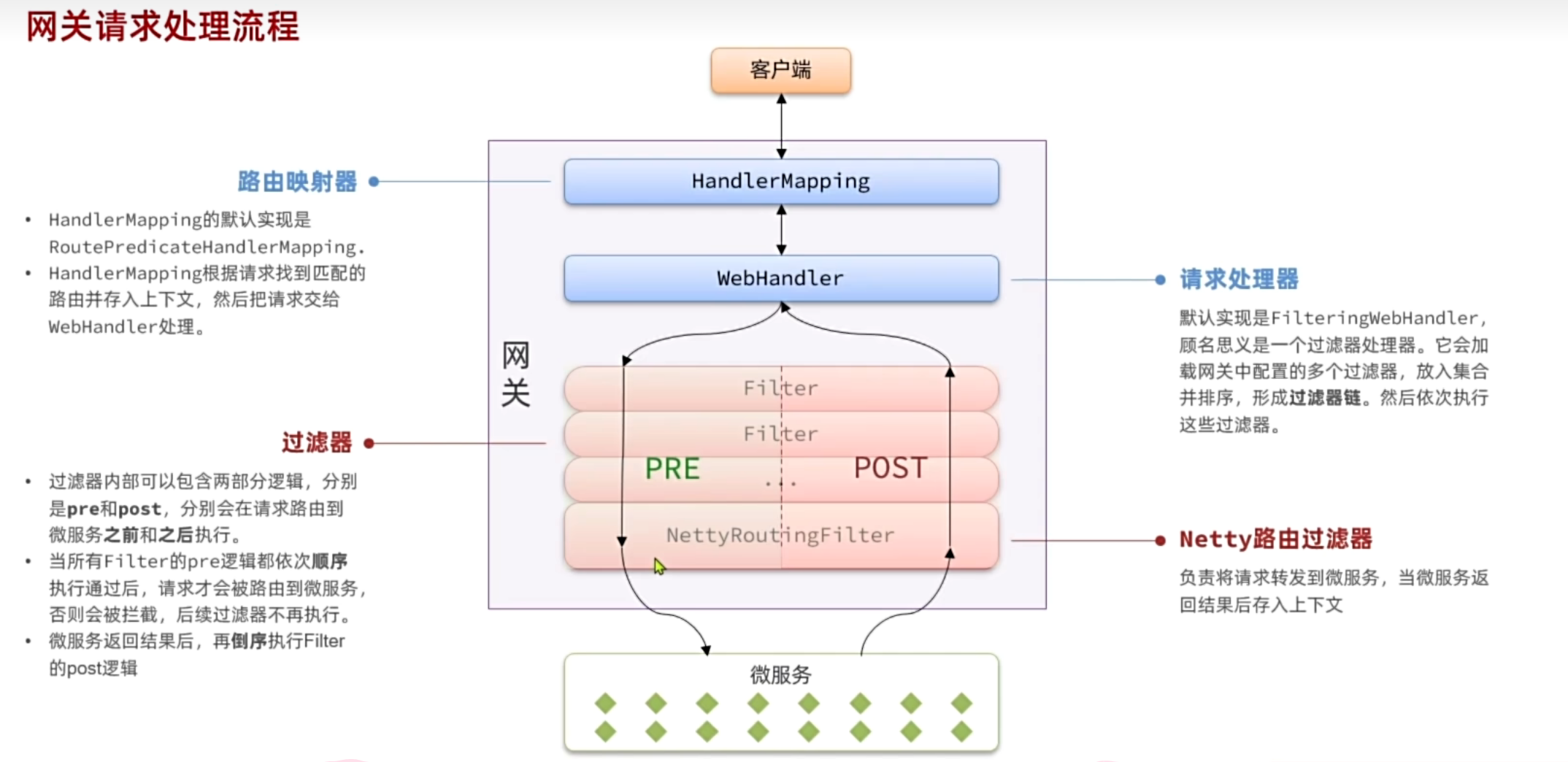
### 登录校验
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们需要实现一个网关过滤器,有两种可选:
|
||||
|
||||
- [ ] **`GatewayFilter`**:路由过滤器,作用范围比较灵活,可以是任意指定的路由`Route`.
|
||||
- [x] **`GlobalFilter`**:全局过滤器,作用范围是所有路由,不可配置。
|
||||
|
||||
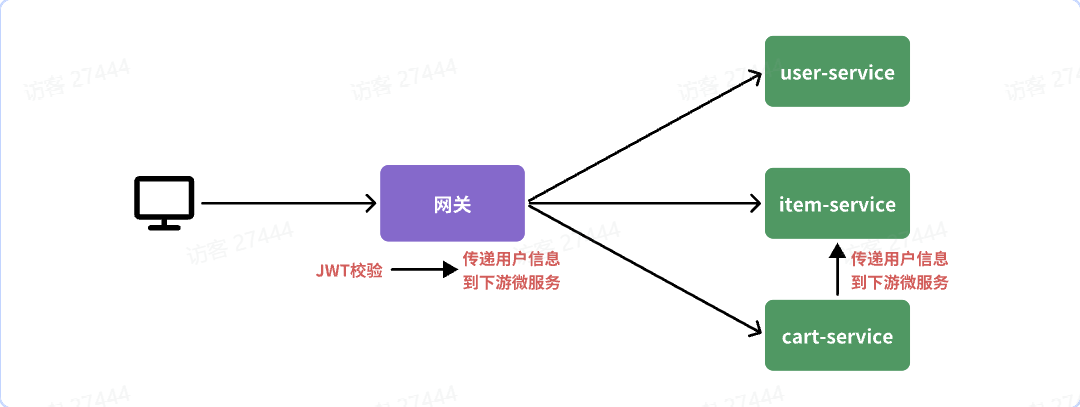
网关需要实现两个功能:1.JWT**校验** 2.将用户信息**传递**给微服务
|
||||
|
||||
#### 网关校验+存用户信息
|
||||
|
||||
```java
|
||||
@Component
|
||||
@RequiredArgsConstructor
|
||||
@EnableConfigurationProperties(AuthProperties.class)
|
||||
public class AuthGlobalFilter implements GlobalFilter, Ordered {
|
||||
|
||||
private final JwtTool jwtTool;
|
||||
|
||||
private final AuthProperties authProperties;
|
||||
|
||||
private final AntPathMatcher antPathMatcher = new AntPathMatcher();
|
||||
|
||||
@Override
|
||||
public Mono<Void> filter(ServerWebExchange exchange, GatewayFilterChain chain) {
|
||||
// 1.获取Request
|
||||
ServerHttpRequest request = exchange.getRequest();
|
||||
// 2.判断是否不需要拦截
|
||||
if(isExclude(request.getPath().toString())){
|
||||
// 无需拦截,直接放行
|
||||
return chain.filter(exchange);
|
||||
}
|
||||
// 3.获取请求头中的token
|
||||
String token = null;
|
||||
List<String> headers = request.getHeaders().get("authorization");
|
||||
if (!CollUtils.isEmpty(headers)) {
|
||||
token = headers.get(0);
|
||||
}
|
||||
// 4.校验并解析token
|
||||
Long userId = null;
|
||||
try {
|
||||
userId = jwtTool.parseToken(token);
|
||||
} catch (UnauthorizedException e) {
|
||||
// 如果无效,拦截
|
||||
ServerHttpResponse response = exchange.getResponse();
|
||||
response.setRawStatusCode(401);
|
||||
return response.setComplete();
|
||||
}
|
||||
|
||||
// 5.如果有效,传递用户信息
|
||||
String userInfo = userId.toString();
|
||||
ServerWebExchange modifiedExchange = exchange.mutate()
|
||||
.request(builder -> builder.header("user-info", userInfo))
|
||||
.build();
|
||||
// 6.放行
|
||||
return chain.filter(modifiedExchange);
|
||||
}
|
||||
|
||||
private boolean isExclude(String antPath) {
|
||||
for (String pathPattern : authProperties.getExcludePaths()) {
|
||||
if(antPathMatcher.match(pathPattern, antPath)){
|
||||
return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
@Override
|
||||
public int getOrder() {
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
- 实现`Ordered`接口中的 `getOrder` 方法,数字越小过滤器执行优先级越高。
|
||||
- `exchange` 可以获得上下文信息。
|
||||
|
||||
|
||||
|
||||
#### 拦截器获取用户
|
||||
|
||||
在Common模块中设置:
|
||||
|
||||
只负责保存 `userinfo` 到 `UserContext` ,不负责拦截,因为拦截在前面的过滤器做了。
|
||||
|
||||
```java
|
||||
public class UserInfoInterceptor implements HandlerInterceptor {
|
||||
@Override
|
||||
public boolean preHandle(HttpServletRequest request, HttpServletResponse response, Object handler) throws Exception {
|
||||
// 1.获取请求头中的用户信息
|
||||
String userInfo = request.getHeader("user-info");
|
||||
// 2.判断是否为空
|
||||
if (StrUtil.isNotBlank(userInfo)) {
|
||||
// 不为空,保存到ThreadLocal
|
||||
UserContext.setUser(Long.valueOf(userInfo));
|
||||
}
|
||||
// 3.放行
|
||||
return true;
|
||||
}
|
||||
|
||||
@Override
|
||||
public void afterCompletion(HttpServletRequest request, HttpServletResponse response, Object handler, Exception ex) throws Exception {
|
||||
// 移除用户
|
||||
UserContext.removeUser();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
配置类:
|
||||
|
||||
```java
|
||||
@Configuration
|
||||
@ConditionalOnClass(DispatcherServlet.class)
|
||||
public class MvcConfig implements WebMvcConfigurer {
|
||||
@Override
|
||||
public void addInterceptors(InterceptorRegistry registry) {
|
||||
registry.addInterceptor(new UserInfoInterceptor());
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
注意:Spring Boot 只会从主启动类所在的包(及其子包)去扫描组件。 `common` 包跟 `item`、`cart` 等微服务模块是平级的,无法被扫描到。解决方法:
|
||||
|
||||
1.在每个微服务的启动类上添加包扫描
|
||||
|
||||
```java
|
||||
@SpringBootApplication(
|
||||
scanBasePackages = {"com.hmall.item","com.hmall.common"}
|
||||
)
|
||||
```
|
||||
|
||||
主包以及common包
|
||||
|
||||
2.在主应用的启动类上用 `@Import`:
|
||||
|
||||
```java
|
||||
@SpringBootApplication
|
||||
@Import(com.hmall.common.interceptors.MvcConfig.class)
|
||||
public class Application { … }
|
||||
```
|
||||
|
||||
**3.前两种方法的问题在于每个微服务模块中都需要写common的引入**
|
||||
|
||||
因此可以把`common` 模块做成 Spring Boot **自动配置**
|
||||
|
||||
1)在`common/src/main/resources/META-INF/spring.factories` 里声明:
|
||||
|
||||
```text
|
||||
org.springframework.boot.autoconfigure.EnableAutoConfiguration=\
|
||||
com.hmall.common.config.MvcConfig
|
||||
```
|
||||
|
||||
2)在 `common` 模块里给 `MvcConfig` 加上
|
||||
|
||||
```java
|
||||
@Configuration
|
||||
@ConditionalOnClass(DispatcherServlet.class) //网关不生效 spring服务生效
|
||||
public class MvcConfig { … }
|
||||
```
|
||||
|
||||
3)然后在任何微服务的 `pom.xml`里只要依赖了这个 common jar,就会自动加载拦截器配置,根本不需要改服务里的 `@SpringBootApplication`。
|
||||
|
||||
|
||||
|
||||
#### OpenFeign传递用户
|
||||
|
||||
前端发起的请求都会经过网关再到微服务,微服务可以轻松获取登录用户信息。但是,有些业务是比较复杂的,请求到达微服务后还需要调用其它多个微服务,**微服务之间的调用**无法传递用户信息,因为**不在一个上下文**(线程)中!
|
||||
|
||||
解决思路:**让每一个由OpenFeign发起的请求自动携带登录用户信息**。要借助Feign中提供的一个拦截器接口:`feign.RequestInterceptor`
|
||||
|
||||
```java
|
||||
public class DefaultFeignConfig {
|
||||
@Bean
|
||||
public RequestInterceptor userInfoRequestInterceptor(){
|
||||
return new RequestInterceptor() {
|
||||
@Override
|
||||
public void apply(RequestTemplate template) {
|
||||
// 获取登录用户
|
||||
Long userId = UserContext.getUser();
|
||||
if(userId == null) {
|
||||
// 如果为空则直接跳过
|
||||
return;
|
||||
}
|
||||
// 如果不为空则放入请求头中,传递给下游微服务
|
||||
template.header("user-info", userId.toString());
|
||||
}
|
||||
};
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
同时,需要在服务调用者的启动类上添加:
|
||||
|
||||
```java
|
||||
@EnableFeignClients(
|
||||
basePackages = "com.hmall.api.client",
|
||||
defaultConfiguration = DefaultFeignConfig.class
|
||||
)
|
||||
```
|
||||
|
||||
|
||||
|
||||
**整体流程图**
|
||||
|
||||
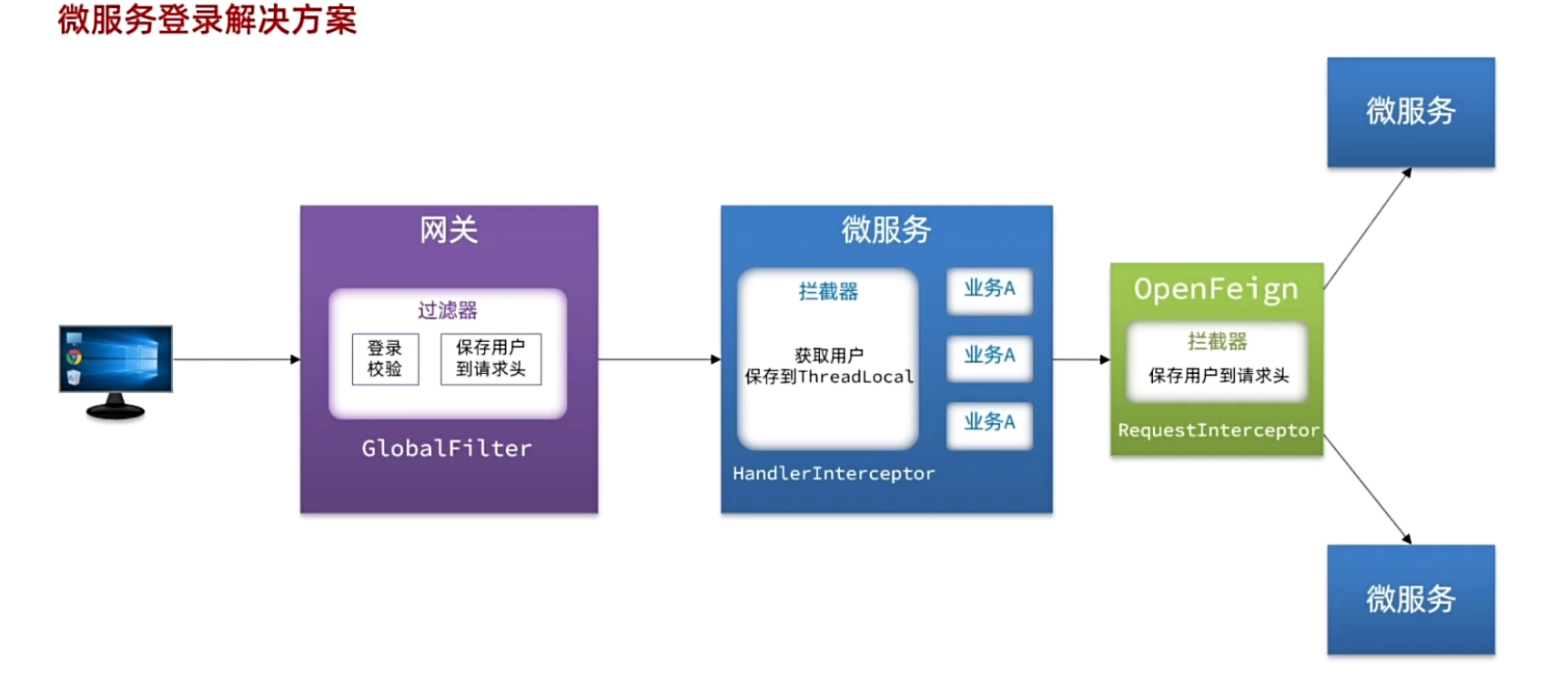
|
||||
|
||||
|
||||
|
||||
## 配置管理
|
||||
|
||||
微服务共享的配置可以统一交给**Nacos**保存和管理,在Nacos控制台修改配置后,Nacos会将配置变更推送给相关的微服务,并且无需重启即可生效,实现**配置热更新**。
|
||||
|
||||
### 配置共享
|
||||
|
||||
**在nacos控制台的配置管理中添加配置文件**
|
||||
|
||||
- `数据库ip`:通过`${hm.db.host:192.168.150.101}`配置了默认值为`192.168.150.101`,同时允许通过`${hm.db.host}`来覆盖默认值
|
||||
|
||||
|
||||
|
||||
**配置读取流程:**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/24/s9s6am-0.png" alt="image-20250524170952380" style="zoom:67%;" />
|
||||
|
||||
微服务整合Nacos配置管理的步骤如下:
|
||||
|
||||
1)引入依赖:
|
||||
|
||||
```xml
|
||||
<!--nacos配置管理-->
|
||||
<dependency>
|
||||
<groupId>com.alibaba.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-alibaba-nacos-config</artifactId>
|
||||
</dependency>
|
||||
<!--读取bootstrap文件-->
|
||||
<dependency>
|
||||
<groupId>org.springframework.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-bootstrap</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2)新建bootstrap.yaml
|
||||
|
||||
在cart-service中的resources目录新建一个bootstrap.yaml文件:
|
||||
|
||||
主要给nacos的信息
|
||||
|
||||
```yml
|
||||
spring:
|
||||
application:
|
||||
name: cart-service # 服务名称
|
||||
profiles:
|
||||
active: dev
|
||||
cloud:
|
||||
nacos:
|
||||
server-addr: 192.168.150.101 # nacos地址
|
||||
config:
|
||||
file-extension: yaml # 文件后缀名
|
||||
shared-configs: # 共享配置
|
||||
- dataId: shared-jdbc.yaml # 共享mybatis配置
|
||||
- dataId: shared-log.yaml # 共享日志配置
|
||||
- dataId: shared-swagger.yaml # 共享日志配置
|
||||
```
|
||||
|
||||
3)修改application.yaml
|
||||
|
||||
```yml
|
||||
server:
|
||||
port: 8082
|
||||
feign:
|
||||
okhttp:
|
||||
enabled: true # 开启OKHttp连接池支持
|
||||
hm:
|
||||
swagger:
|
||||
title: 购物车服务接口文档
|
||||
package: com.hmall.cart.controller
|
||||
db:
|
||||
database: hm-cart
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 配置热更新
|
||||
|
||||
有很多的业务相关参数,将来可能会根据实际情况临时调整,如何不重启服务,直接更改配置文件生效呢?
|
||||
|
||||
示例:购物车中的商品上限数量需动态调整。
|
||||
|
||||
1)在nacos中添加配置
|
||||
|
||||
在nacos中添加一个配置文件,将购物车的上限数量添加到配置中:
|
||||
|
||||
文件的dataId格式:
|
||||
|
||||
```text
|
||||
[服务名]-[spring.active.profile].[后缀名]
|
||||
```
|
||||
|
||||
文件名称由三部分组成:
|
||||
|
||||
- **`服务名`**:我们是购物车服务,所以是`cart-service`
|
||||
- **`spring.active.profile`**:就是spring boot中的`spring.active.profile`,可以省略,则所有profile共享该配置(不管local还是dev还是prod)
|
||||
- **`后缀名`**:例如yaml
|
||||
|
||||
示例:`cart-service.yaml`
|
||||
|
||||
```YAML
|
||||
hm:
|
||||
cart:
|
||||
maxAmount: 1 # 购物车商品数量上限
|
||||
```
|
||||
|
||||
|
||||
|
||||
2)在微服务中配置
|
||||
|
||||
```java
|
||||
@Data
|
||||
@Component
|
||||
@ConfigurationProperties(prefix = "hm.cart")
|
||||
public class CartProperties {
|
||||
private Integer maxAmount;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
下次,只需改nacos中的配置,即可实现热更新。
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user