zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Commit on 2025/04/03 周四 17:42:27.35

Browse Source
This commit is contained in:
zhangsan 2025-04-03 17:42:27 +08:00
parent 5545322a6e
commit 18feba745b
9 changed files with 769 additions and 239 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

101
科研/凸优化问题求解.md
View File

@ -2,21 +2,74 @@
### 核心概念 ### 核心概念
1. **凸函数** #### 凸函数
定义：$f(x)$ 是凸函数当且仅当
定义：$f(x)$ 是凸函数当且仅当
$$
f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2), \quad \forall x_1,x_2 \in \text{dom}(f), \theta \in [0,1]
$$
示例：$f(x)=x^2$, $f(x)=e^x$
**验证 $f(x) = x^2$ 是凸函数：**
代入 $f(x) = x^2$：
$$
(\theta x_1 + (1-\theta) x_2)^2 \leq \theta x_1^2 + (1-\theta) x_2^2
$$
1. 展开左边：
$$ $$
f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2), \quad \forall x_1,x_2 \in \text{dom}(f), \theta \in [0,1] (\theta x_1 + (1-\theta) x_2)^2 = \theta^2 x_1^2 + 2\theta(1-\theta)x_1x_2 + (1-\theta)^2 x_2^2
$$ $$
- 示例：$f(x)=x^2$, $f(x)=e^x$ 2. 右边：
2. **凸集**
定义：集合$X$是凸集当且仅当
$$ $$
\forall x_1,x_2 \in X, \theta \in [0,1] \Rightarrow \theta x_1 + (1-\theta)x_2 \in X \theta x_1^2 + (1-\theta) x_2^2
$$ $$
- 示例：超平面、球体 3. 计算差值（右边减左边）：
$$
\theta x_1^2 + (1-\theta) x_2^2 - \theta^2 x_1^2 - 2\theta(1-\theta)x_1x_2 - (1-\theta)^2 x_2^2
$$
化简：
$$
= \theta(1-\theta)x_1^2 + (1-\theta)\theta x_2^2 - 2\theta(1-\theta)x_1x_2
$$
$$
= \theta(1-\theta)(x_1^2 + x_2^2 - 2x_1x_2)
$$
$$
= \theta(1-\theta)(x_1 - x_2)^2 \geq 0
$$
4. **结论**：
- 因为 $\theta \in [0,1]$，所以 $\theta(1-\theta) \geq 0$，且 $(x_1 - x_2)^2 \geq 0$。
- 因此，右边减左边 $\geq 0$，即：
$$
(\theta x_1 + (1-\theta) x_2)^2 \leq \theta x_1^2 + (1-\theta) x_2^2
$$
- **$f(x)=x^2$ 满足凸函数的定义**。
#### 凸集
**集合中任意两点的连线仍然完全包含在该集合内**。换句话说，这个集合没有“凹陷”的部分。
定义：集合$X$是凸集当且仅当
$$
\forall x_1,x_2 \in X, \theta \in [0,1] \Rightarrow \theta x_1 + (1-\theta)x_2 \in X
$$
- 示例：超平面、球体
### 凸优化问题标准形式 ### 凸优化问题标准形式
@ -385,29 +438,19 @@ $$
##### 情况1：λ=0 ##### 情况1：λ=0
代入方程(1): | **步骤** | **计算过程** | **结果** |
2x + 0 = 0 ⇒ x=0 | ---------- | ------------------------------ | -------- |
| 平稳性条件 | $2x + 0 = 0 \Rightarrow x = 0$ | $x = 0$ |
检查原始可行性： | 原始可行性 | $g(0) = 0 - 1 = -1 \leq 0$ | 满足 |
g(0)=0-1=-1≤0 ✔ | 对偶可行性 | $\lambda = 0 \geq 0$ | 满足 |
| 互补松弛性 | $0 \cdot (-1) = 0$ | 满足 |
检查对偶可行性：
λ=0≥0 ✔
互补松弛性：
0·(-1)=0 ✔
所以x=0, λ=0是一个可能的解。
##### 情况2：x=1 ##### 情况2：x=1
代入方程(1): | **步骤** | **计算过程** | **结果** |
2·1 + λ = 0 ⇒ λ=-2 | ---------- | --------------------------------------------- | ---------------------- |
| 平稳性条件 | $2(1) + \lambda = 0 \Rightarrow \lambda = -2$ | $\lambda = -2$ |
检查对偶可行性： | 对偶可行性 | $\lambda = -2 \geq 0$ | **不满足**（乘子为负） |
λ=-2≥0 ✖ 不满足
因此这种情况被排除。
**唯一满足所有KKT条件的解是x=0, λ=0。** **唯一满足所有KKT条件的解是x=0, λ=0。**

129
科研/数学基础.md
View File

@ -267,135 +267,6 @@ $$
## 范数
### **L2范数定义**：
对于一个向量 $\mathbf{w} = [w_1, w_2, \dots, w_n]$，L2 范数定义为
$$
\|\mathbf{w}\|_2 = \sqrt{w_1^2 + w_2^2 + \dots + w_n^2}
$$
假设一个权重向量为 $\mathbf{w} = [3, -4]$，则
$$
\|\mathbf{w}\|_2 = \sqrt{3^2 + (-4)^2} = \sqrt{9+16} = \sqrt{25} = 5.
$$
**用途**：
- **正则化（L2正则化/权重衰减）**：在训练过程中，加入 L2 正则项有助于防止模型过拟合。正则化项通常是权重的 L2 范数的平方，例如
$$
\lambda \|\mathbf{w}\|_2^2
$$
其中 $\lambda$ 是正则化系数。
- **梯度裁剪**：在 RNN 等深度网络中，通过计算梯度的 L2 范数来判断是否需要对梯度进行裁剪，从而防止梯度爆炸。
**具体例子**：
假设我们有一个简单的线性回归模型，损失函数为均方误差（MSE）：
$$
L(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2
$$
其中，$N$ 是样本数量，$y_i$ 是第 $i$ 个样本的真实值，$\mathbf{x}_i$ 是第 $i$ 个样本的特征向量，$\mathbf{w}$ 是权重向量。
加入 L2 正则项后，新的损失函数为：
$$
L_{\text{reg}}(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_2^2
$$
在训练过程中，优化算法会同时最小化原始损失函数和正则项，从而在拟合训练数据的同时，避免权重值过大。
**梯度更新**
在梯度下降算法中，权重 $\mathbf{w}$ 的更新公式为：
$$
\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla L_{\text{reg}}(\mathbf{w})
$$
其中，$\eta$ 是学习率，$\nabla L_{\text{reg}}(\mathbf{w})$ 是损失函数关于 $\mathbf{w}$ 的梯度。
对于加入 L2 正则项的损失函数，梯度为：
$$
\nabla L_{\text{reg}}(\mathbf{w}) = \nabla L(\mathbf{w}) + 2\lambda \mathbf{w}
$$
因此，权重更新公式变为：
$$
\mathbf{w} \leftarrow \mathbf{w} - \eta (\nabla L(\mathbf{w}) + 2\lambda \mathbf{w})
$$
通过加入 L2 正则项，模型在训练过程中不仅会最小化原始损失函数，还会尽量减小权重的大小，从而避免过拟合。正则化系数 $\lambda$ 控制着正则化项的强度，较大的 $\lambda$ 会导致权重更小，模型更简单，但可能会欠拟合；较小的 $\lambda$ 则可能无法有效防止过拟合。因此，选择合适的 $\lambda$ 是使用 L2 正则化的关键。
### Frobenius 范数
对于一个矩阵 $A \in \mathbb{R}^{m \times n}$，其 Frobenius 范数定义为
$$
\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} a_{ij}^2}
$$
这个定义与向量 L2 范数类似，只不过是对矩阵中所有元素取平方和后再开平方。
如果矩阵 $A$ 的奇异值为 $\sigma_1, \sigma_2, \ldots, \sigma_n$，则：
$$
\|A\|_F = \sqrt{\sum_{i=1}^n \sigma_i^2}
$$
这使得 Frobenius 范数在低秩近似和矩阵分解（如 SVD）中非常有用。
**迹和 Frobenius 范数的关系**：
$$
\|A\|_F^2 = \text{tr}(A^* A)
$$
这表明 Frobenius 范数的平方就是 $A^* A$ 所有特征值之和。而 $A^* A$ 的特征值开方就是A的奇异值。
**权重为向量的情况**
当模型的输出是标量时（如单变量线性回归或二分类逻辑回归）：
- **输入特征**：$\mathbf{x}_i \in \mathbb{R}^d$（向量）
- **权重形状**：$\mathbf{w} \in \mathbb{R}^d$（向量）
- **预测公式**：
$$
\hat{y}_i = \mathbf{w}^\top \mathbf{x}_i
$$
其中 $\hat{y}_i$ 是标量输出。
---
**权重为矩阵的情况**
当模型的输出是向量时（如多变量回归、神经网络全连接层）：
- **输入特征**：$\mathbf{x}_i \in \mathbb{R}^d$（向量）
- **输出维度**：$\hat{\mathbf{y}}_i \in \mathbb{R}^m$（向量）
- **权重形状**：$W \in \mathbb{R}^{m \times d}$（矩阵）
- **预测公式**：
$$
\hat{\mathbf{y}}_i = W \mathbf{x}_i + \mathbf{b}
$$
其中 $\mathbf{b} \in \mathbb{R}^m$ 是偏置向量。
## 期望、方差、协方差 ## 期望、方差、协方差
### 期望 ### 期望

269
科研/线性代数.md
View File

@ -1,6 +1,6 @@
## 线性代数 # 线性代数
### 线性变换 ## 线性变换
每列代表一个基向量，行数代码这个基向量所张成空间的维度，二行三列表示二维空间的三个基向量。 每列代表一个基向量，行数代码这个基向量所张成空间的维度，二行三列表示二维空间的三个基向量。
@ -14,7 +14,7 @@
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{i} & \mathbf{j} & \mathbf{k} \\ | & | & | \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{i} & \mathbf{j} & \mathbf{k} \\ | & | & | \end{bmatrix}
$$ $$
#### **矩阵乘向量** ### **矩阵乘向量**
在 3blue1brown 的“线性代数的本质”系列中，他把矩阵乘向量的运算解释为**线性组合**和**线性变换**的过程。具体来说： 在 3blue1brown 的“线性代数的本质”系列中，他把矩阵乘向量的运算解释为**线性组合**和**线性变换**的过程。具体来说：
@ -55,7 +55,7 @@
#### **矩阵乘矩阵** ### **矩阵乘矩阵**
当你有两个矩阵 $ A $ 和 $ B $，矩阵乘法 $ AB $ 实际上代表的是： 当你有两个矩阵 $ A $ 和 $ B $，矩阵乘法 $ AB $ 实际上代表的是：
@ -102,7 +102,7 @@ $$
### 行列式 ## 行列式
3blue1brown讲解行列式时，核心在于用几何直观来理解行列式的意义： 3blue1brown讲解行列式时，核心在于用几何直观来理解行列式的意义：
@ -121,23 +121,23 @@ $$
### 逆矩阵、列空间、零空间 ## 逆矩阵、列空间、零空间
#### **逆矩阵** ### **逆矩阵**
逆矩阵描述了一个矩阵所代表的线性变换的**“反过程”**。假设矩阵 $A$ 对空间做了某种变换（比如旋转、拉伸或压缩），那么 $A^{-1}$ 就是把这个变换“逆转”，把变换后的向量再映射回原来的位置。 逆矩阵描述了一个矩阵所代表的线性变换的**“反过程”**。假设矩阵 $A$ 对空间做了某种变换（比如旋转、拉伸或压缩），那么 $A^{-1}$ 就是把这个变换“逆转”，把变换后的向量再映射回原来的位置。
前提是$A$ 是可逆的，即它对应的变换不会把空间压缩到更低的维度。 前提是$A$ 是可逆的，即它对应的变换不会把空间压缩到更低的维度。
#### 秩 ### 秩
秩等于矩阵列向量（或行向量）**所生成的空间的维数**。例如，在二维中，如果一个 $2 \times 2$ 矩阵的秩是 2，说明这个变换把平面“充满”；如果秩为 1，则所有输出都落在一条直线上，说明变换“丢失”了一个维度。 秩等于矩阵列向量（或行向量）**所生成的空间的维数**。例如，在二维中，如果一个 $2 \times 2$ 矩阵的秩是 2，说明这个变换把平面“充满”；如果秩为 1，则所有输出都落在一条直线上，说明变换“丢失”了一个维度。
#### 列空间 ### 列空间
列空间是矩阵所有列向量的线性组合所构成的集合（也可以说所有可能的**输出向量**$A\mathbf{x}$所构成的集合）。 比如一个二维变换的列空间可能是整个平面，也可能只是一条直线，这取决于矩阵的秩。 列空间是矩阵所有列向量的线性组合所构成的集合（也可以说所有可能的**输出向量**$A\mathbf{x}$所构成的集合）。 比如一个二维变换的列空间可能是整个平面，也可能只是一条直线，这取决于矩阵的秩。
#### 零空间 ### 零空间
零空间（又称核、kernel）是所有在该矩阵作用（线性变换$A$）下变成零向量的**输入向量**的集合。 零空间（又称核、kernel）是所有在该矩阵作用（线性变换$A$）下变成零向量的**输入向量**的集合。
@ -145,7 +145,7 @@ $$
零空间解释了$Ax=0$的解的集合，就是齐次的通解。如果满秩，零空间只有唯一解零向量。 零空间解释了$Ax=0$的解的集合，就是齐次的通解。如果满秩，零空间只有唯一解零向量。
#### 求解线性方程 ### 求解线性方程
设线性方程组写作 设线性方程组写作
$$ $$
@ -161,7 +161,7 @@ $$
### 基变换 ## 基变换
新基下的变换矩阵 $A_C$ 为： 新基下的变换矩阵 $A_C$ 为：
$$ $$
@ -176,7 +176,7 @@ $A$：线性变换 $T$ 在**原基**下的矩阵表示
### 点积、哈达马积 ## 点积、哈达马积
**向量点积（Dot Product）** **向量点积（Dot Product）**
@ -218,7 +218,7 @@ $$
### 特征值和特征向量 ## 特征值和特征向量
设矩阵： 设矩阵：
@ -311,7 +311,7 @@ $$
### 矩阵乘法 ## 矩阵乘法
**全连接神经网络** **全连接神经网络**
@ -427,7 +427,7 @@ $$
### 奇异值 ## 奇异值
**定义** **定义**
@ -453,7 +453,7 @@ $$
--- ---
**计算** ### 奇异值求解
奇异值可以通过计算矩阵 $A^T A$ 或 $A A^T$ 的特征值的**平方根**得到。 奇异值可以通过计算矩阵 $A^T A$ 或 $A A^T$ 的特征值的**平方根**得到。
@ -509,7 +509,236 @@ $$
### 矩阵的迹 ### 奇异值分解
给定一个实矩阵 $A$（形状为 $m \times n$），SVD 是将它分解为：
$$
A = U \Sigma V^T
$$
1. **构造 $A^T A$**
- 计算对称矩阵 $A^T A$（$n \times n$）
2. **求解 $A^T A$ 的特征值和特征向量**
- 设特征值为 $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_n \geq 0$
- 对应特征向量为 $\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n$
3. **计算奇异值**
- $\sigma_i = \sqrt{\lambda_i}$
4. **构造矩阵 $V$**
- 将*正交归一*的特征向量作为列向量：$V = [\mathbf{v}_1 | \mathbf{v}_2 | \dots | \mathbf{v}_n]$
5. **求矩阵 $U$**
- 对每个非零奇异值：$\mathbf{u}_i = \frac{A \mathbf{v}_i}{\sigma_i}$
- 标准化（保证向量长度为 1）后组成 $U = [\mathbf{u}_1 | \mathbf{u}_2 | \dots | \mathbf{u}_m]$
6. **构造 $\Sigma$**
- 对角线放置奇异值：$\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_p)$，$p=\min(m,n)$
## 范数
### **L2范数定义**：
对于一个向量 $\mathbf{w} = [w_1, w_2, \dots, w_n]$，L2 范数定义为
$$
\|\mathbf{w}\|_2 = \sqrt{w_1^2 + w_2^2 + \dots + w_n^2}
$$
假设一个权重向量为 $\mathbf{w} = [3, -4]$，则
$$
\|\mathbf{w}\|_2 = \sqrt{3^2 + (-4)^2} = \sqrt{9+16} = \sqrt{25} = 5.
$$
**用途**：
- **正则化（L2正则化/权重衰减）**：在训练过程中，加入 L2 正则项有助于防止模型过拟合。正则化项通常是权重的 L2 范数的平方，例如
$$
\lambda \|\mathbf{w}\|_2^2
$$
其中 $\lambda$ 是正则化系数。
- **梯度裁剪**：在 RNN 等深度网络中，通过计算梯度的 L2 范数来判断是否需要对梯度进行裁剪，从而防止梯度爆炸。
**具体例子**：
假设我们有一个简单的线性回归模型，损失函数为均方误差（MSE）：
$$
L(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2
$$
其中，$N$ 是样本数量，$y_i$ 是第 $i$ 个样本的真实值，$\mathbf{x}_i$ 是第 $i$ 个样本的特征向量，$\mathbf{w}$ 是权重向量。
加入 L2 正则项后，新的损失函数为：
$$
L_{\text{reg}}(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_2^2
$$
在训练过程中，优化算法会同时最小化原始损失函数和正则项，从而在拟合训练数据的同时，避免权重值过大。
**梯度更新**
在梯度下降算法中，权重 $\mathbf{w}$ 的更新公式为：
$$
\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla L_{\text{reg}}(\mathbf{w})
$$
其中，$\eta$ 是学习率，$\nabla L_{\text{reg}}(\mathbf{w})$ 是损失函数关于 $\mathbf{w}$ 的梯度。
对于加入 L2 正则项的损失函数，梯度为：
$$
\nabla L_{\text{reg}}(\mathbf{w}) = \nabla L(\mathbf{w}) + 2\lambda \mathbf{w}
$$
因此，权重更新公式变为：
$$
\mathbf{w} \leftarrow \mathbf{w} - \eta (\nabla L(\mathbf{w}) + 2\lambda \mathbf{w})
$$
通过加入 L2 正则项，模型在训练过程中不仅会最小化原始损失函数，还会尽量减小权重的大小，从而避免过拟合。正则化系数 $\lambda$ 控制着正则化项的强度，较大的 $\lambda$ 会导致权重更小，模型更简单，但可能会欠拟合；较小的 $\lambda$ 则可能无法有效防止过拟合。因此，选择合适的 $\lambda$ 是使用 L2 正则化的关键。
### 矩阵的元素级范数
L0范数（但它 **并不是真正的范数**）：
$$
\|A\|_0 = \text{Number of non-zero elements in } A = \sum_{i=1}^{m} \sum_{j=1}^{n} \mathbb{I}(a_{ij} \neq 0)
$$
其中：
- $\mathbb{I}(\cdot)$ 是指示函数（若 $a_{ij} \neq 0$ 则取 1，否则取 0）。
- 如果矩阵 $A$ 有 $k$ 个非零元素，则 $\|A\|_0 = k$。
1. **衡量稀疏性**：
- $\|A\|_0$ **越小**，矩阵 $A$ 越稀疏（零元素越多）。
- 在压缩感知、低秩矩阵恢复、稀疏编码等问题中，常用 $L_0$ 范数来 **约束解的稀疏性**。
2. **非凸、非连续、NP难优化**：
- $L_0$ 范数是 **离散的**，导致优化问题通常是 **NP难** 的（无法高效求解）。
- 因此，实际应用中常用 **$L_1$ 范数**（绝对值之和）作为凸松弛替代：
$$
\|A\|_1 = \sum_{i,j} |a_{ij}|
$$
NP难问题：
可以在多项式时间内 **验证一个解是否正确**，但 **不一定能在多项式时间内找到解**。
L1范数：元素绝对值和
$$
\|A\|_1 = \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|
$$
| 范数类型 | 定义 | 性质 | 优化难度 | 用途 |
| --------- | -------------------------------------- | ------------------ | ---------- | -------------- |
| **$L_0$** | $\sum_{i,j} \mathbb{I}(a_{ij} \neq 0)$ | 非凸、离散、不连续 | NP难 | 精确稀疏性控制 |
| **$L_1$** | $\sum_{i,j} |a_{ij}|$ | 凸、连续 | 可高效求解 | 稀疏性近似 |
### 矩阵的核范数
核范数，又称为**迹范数**（trace norm），是矩阵范数的一种，定义为矩阵所有奇异值之和。对于一个矩阵 $A$（假设其奇异值为 $\sigma_1, \sigma_2, \dots, \sigma_r$），其核范数定义为：
$$
\|A\|_* = \sum_{i=1}^{r} \sigma_i,
$$
其中 $r$ 是矩阵 $A$ 的秩。
**核范数的主要特点**
1. 凸性
- 核范数是一个凸函数，因此在优化问题中**常用作替代矩阵秩**的惩罚项（因为直接最小化矩阵秩是一个NP困难的问题）。
2. 低秩逼近
- 在矩阵补全、低秩矩阵恢复等应用中，核范数被用来鼓励矩阵解具有**低秩**性质，因其是矩阵秩的凸松弛。
3. 与SVD的关系
- 核范数直接依赖于矩阵的奇异值，计算时通常需要**奇异值分解**（SVD）。
### Frobenius 范数
对于一个矩阵 $A \in \mathbb{R}^{m \times n}$，其 Frobenius 范数定义为
$$
\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} a_{ij}^2}
$$
这个定义与向量 $L2$ 范数类似，只不过是对矩阵中所有元素取平方和后再开平方。
如果矩阵 $A$ 的奇异值为 $\sigma_1, \sigma_2, \ldots, \sigma_n$，则：
$$
\|A\|_F = \sqrt{\sum_{i=1}^n \sigma_i^2}
$$
这使得 Frobenius 范数在低秩近似和矩阵分解（如 SVD）中非常有用。
**迹和 Frobenius 范数的关系**：
$$
\|A\|_F^2 = \text{tr}(A^* A)
$$
这表明 Frobenius 范数的平方就是 $A^* A$ 所有特征值之和。而 $A^* A$ 的特征值开方就是A的奇异值。
**权重为向量的情况**
当模型的输出是标量时（如单变量线性回归或二分类逻辑回归）：
- **输入特征**：$\mathbf{x}_i \in \mathbb{R}^d$（向量）
- **权重形状**：$\mathbf{w} \in \mathbb{R}^d$（向量）
- **预测公式**：
$$
\hat{y}_i = \mathbf{w}^\top \mathbf{x}_i
$$
其中 $\hat{y}_i$ 是标量输出。
---
**权重为矩阵的情况**
当模型的输出是向量时（如多变量回归、神经网络全连接层）：
- **输入特征**：$\mathbf{x}_i \in \mathbb{R}^d$（向量）
- **输出维度**：$\hat{\mathbf{y}}_i \in \mathbb{R}^m$（向量）
- **权重形状**：$W \in \mathbb{R}^{m \times d}$（矩阵）
- **预测公式**：
$$
\hat{\mathbf{y}}_i = W \mathbf{x}_i + \mathbf{b}
$$
其中 $\mathbf{b} \in \mathbb{R}^m$ 是偏置向量。
## 矩阵的迹
**迹的定义** **迹的定义**
@ -557,7 +786,7 @@ $$
### 酉矩阵 ## 酉矩阵
酉矩阵是一种复矩阵，其满足下面的条件：对于一个 $n \times n$ 的复矩阵 $U$，如果有 酉矩阵是一种复矩阵，其满足下面的条件：对于一个 $n \times n$ 的复矩阵 $U$，如果有
@ -599,7 +828,7 @@ $$
### 对称非负矩阵分解 ## 对称非负矩阵分解
$$ $$
A≈HH^T A≈HH^T

97
科研/草稿.md
View File

@ -1,47 +1,74 @@
- # FCM算法时间复杂度分析 ### 4.2.3 ADMM求解的变量与步骤详解
## 1. FCM算法的步骤与时间复杂度 #### 1. 变量定义与作用
- **输入变量**：
- $A_{pre}$：初始邻接矩阵（优化前的网络拓扑）。
- $P$：对称的0-1矩阵，用于标记 $A_{pre}$ 中非零元素的位置（保持已有边不变）。
- $A'_{max}$：功率最大时的邻接矩阵的补集（$A'_{maxij} = 1$ 表示 $A_{maxij} = 0$，即不允许新增边）。
- $\alpha$：权衡稀疏性（$L_1$ 范数）和低秩性（核范数）的系数。
- **iters**：ADMM迭代次数。
### **1. 初始化步骤** - **中间变量**：
- **初始化簇中心**：需要 $O(K)$ 时间（$K$ 是簇数） - **$D_1, D_2$**：临时变量，用于投影步骤的中间计算。
- **初始化隶属度矩阵 $U$**（$n \times K$ 矩阵）：$O(nK)$ - $D_1 = A^*$：来自附录A的推导（可能是对偶变量或中间解）。
- $D_2 = R^* + A_{pre}$：结合残差 $R^*$ 和初始矩阵 $A_{pre}$ 的中间结果。
- **$M$**：残差计算的辅助矩阵，可能与约束 $A \odot P = A_{pre} \odot P$ 相关。
- **$temp\_R, temp\_A$**：内层循环的临时变量，用于梯度投影的残差计算。
- **$X, Y$**：对偶变量（拉格朗日乘子），分别对应两个约束：
- $X$：约束 $A \odot P = A_{pre} \odot P$ 的对偶变量。
- $Y$：约束 $A \odot A'_{max} = 0$ 的对偶变量。
- **$Z1, Z2$**：辅助变量，用于解耦目标函数中的核范数和 $L_1$ 范数：
- $Z1$：与核范数 $\|A\|_*$ 相关的辅助变量。
- $Z2$：与 $L_1$ 范数 $\|A\|_1$ 相关的辅助变量。
- **$U1, U2$**：拉格朗日乘子，用于ADMM的对偶上升步骤：
- $U1$：对应 $Z1$ 的约束 $A = Z1$。
- $U2$：对应 $Z2$ 的约束 $A = Z2$。
### **2. 更新隶属度** ---
- 每个数据点 $a_{ij}$ 计算与每个簇中心 $c_k$ 的距离：$O(K)$
- 更新所有数据点的隶属度矩阵：$O(nK^2)$
### **3. 更新簇中心** #### 2. 算法步骤详解
- 计算每个簇的新中心（加权平均）：$O(nK)$ ##### (S.1) 更新原始变量 $A$（ADMM的 $x$ 步）
- 总体簇中心更新：$O(nK)$ 通过内层循环（投影和对偶上升）更新 $A$，确保其满足两个约束：
1. **投影到 $A \odot P = A_{pre} \odot P$**（保持已有边不变）：
- **行4-11**：梯度投影法迭代更新 $R$（残差）。
- $temp\_R^{k+1} = M - X^k \odot A_{pre}$：计算当前残差（$M$ 可能是约束的右端项）。
- $X^{k+1} = X^k + \beta (A_{pre} \odot temp\_R^{k+1})$：对偶变量 $X$ 的梯度上升（步长 $\beta$）。
- **本质**：通过迭代强制 $A$ 在 $P$ 标记的位置与 $A_{pre}$ 一致。
### **4. 判断收敛** 2. **投影到 $A \odot A'_{max} = 0$**（禁止新增边）：
- 计算簇中心变化量 $\Delta C$：$O(K)$ - **行13-17**：类似地，更新 $Y$：
- $temp\_A^{k+1} = D_2 - Y^k \odot A'_{max}$：残差计算。
- $Y^{k+1} = Y^k + \gamma (A'_{max} \odot temp\_A^{k+1})$：对偶变量 $Y$ 的更新（步长 $\gamma$）。
### **5. 量化处理** ##### (S.2) 更新辅助变量 $Z1, Z2$（ADMM的 $z$ 步）
- 将元素分配到簇并替换值：$O(nK)$ 通过阈值操作分离目标函数的两部分：
1. **$Z1^{t+1} = T_r(A^{t+1} + U1^t)$**：
- $T_r(\cdot)$：奇异值阈值算子（核范数投影）。
- 对 $A + U1$ 做SVD分解，保留前 $r$ 个奇异值（$r$ 由低秩性需求决定）。
- **作用**：强制 $A$ 低秩。
## 2. 总时间复杂度 2. **$Z2^{t+1} = S_{\alpha}(A^{t+1} + U2^t)$**：
- $S_{\alpha}(\cdot)$：软阈值算子（$L_1$ 范数投影）。
- 对 $A + U2$ 的每个元素：$\text{sign}(x) \cdot \max(|x| - \alpha, 0)$。
- **作用**：促进 $A$ 的稀疏性。
每次迭代的总时间复杂度： ##### (S.3) 更新拉格朗日乘子 $U1, U2$（ADMM的对偶上升）
$$ 通过残差调整乘子：
O(nK^2) + O(nK) + O(K) \approx O(nK^2) - $U1^{t+1} = U1^t + A^{t+1} - Z1^{t+1}$：核范数约束的乘子更新。
$$ - $U2^{t+1} = U2^t + A^{t+1} - Z2^{t+1}$：$L_1$ 范数约束的乘子更新。
- **作用**：惩罚 $A$ 与辅助变量 $Z1, Z2$ 的偏差，推动收敛。
其中： ---
- $n$：数据点数量
- $K$：簇数量
## 3. 初始簇中心选取优化方法的时间复杂度 #### 3. 关键点总结
1. **投影步骤**：内层循环通过梯度法将 $A$ 投影到两个约束集合（保持已有边 + 禁止新增边）。
2. **变量解耦**：$Z1, Z2$ 分离低秩和稀疏目标，ADMM通过交替更新协调二者。
3. **凸性保证**：核范数和 $L_1$ 范数均为凸函数，ADMM能收敛到全局最优解。
4. **并行性**：每个节点可独立运行算法（行1注释），适合分布式网络优化。
- 选择 $K$ 个簇中心时： ---
- 需要计算候选集内元素间最小距离
- 每次选择复杂度：$O(n^2)$
- 总体选择复杂度：$O(Kn^2)$
## 4. 图片分析结论 #### 可能的疑问与验证
- **$M$ 的具体定义**：文中未明确，可能是 $A_{pre} \odot P$ 或其他约束右端项。
图片中的时间复杂度分析是合理的： - **$D_1, D_2$ 的推导**：需参考附录A的公式（4-33）和（4-40），可能涉及对偶问题的转换。
- **标准FCM算法**：$O(nK^2)$ - **步长 $\beta, \gamma$**：通常需手动调参或通过线搜索确定。
- **优化簇中心选择**：$O(n^3)$
该分析准确反映了FCM算法的计算复杂度。

79
科研/郭款论文.md
View File

@ -253,24 +253,24 @@ PAM 改进了离群点的问题，但它依然属于硬性聚类方法，且计
#### **FCM算法** #### **FCM算法**
FCM的目标是将矩阵中的元素聚类到K个簇中，每个元素通过**隶属度**（概率值）表示其属于各簇的程度。以下是算法的详细步骤： FCM的目标是将矩阵中的元素聚类到$K$个簇中，每个元素通过**隶属度**（概率值）表示其属于各簇的程度。以下是算法的详细步骤：
**1. 初始化** **1. 初始化**
- 输入：待聚类的矩阵 \( A \)（例如邻接矩阵）。 - 输入：待聚类的矩阵 $A$（例如邻接矩阵）。
- 设置：簇数 \( K \)、模糊因子 \( m \)（通常取2）、收敛精度 \( $\epsilon$ \)、最大迭代次数。 - 设置：簇数 $K$ 、模糊因子 $m$（通常取2）、收敛精度 $\epsilon$ 、最大迭代次数。
- 初始化：随机生成隶属度矩阵 \( U \) 和簇中心 \( C \)。 - 初始化：随机生成隶属度矩阵 $U$ 和簇中心 $C$ 。
**2. 更新隶属度** **2. 更新隶属度**
对于每个元素 \( $a_{ij} $\)，计算其属于簇 \( k \) 的隶属度 \($ \mu_k(a_{ij})$ \)： 对于每个元素 $a_{ij} $，计算其属于簇 $k$ 的隶属度 $ \mu_k(a_{ij})$ ：
$$ $$
\mu_k(a_{ij}) = \frac{1}{\sum_{l=1}^{K} \left( \frac{\|a_{ij} - c_k\|}{\|a_{ij} - c_l\|} \right)^{2/(m-1)}} \mu_k(a_{ij}) = \frac{1}{\sum_{l=1}^{K} \left( \frac{\|a_{ij} - c_k\|}{\|a_{ij} - c_l\|} \right)^{2/(m-1)}}
$$ $$
- \( \|$a_{ij} - c_k$\| \)：元素 \($ a_{ij}$ \) 到簇中心 \( $c_k$ \) 的距离（通常用欧氏距离）。 - \|$a_{ij} - c_k$\| ：元素 \($ a_{ij}$ \) 到簇中心 \( $c_k$ \) 的距离（通常用欧氏距离）。
- \( m \)：模糊因子，控制聚类的模糊程度（\( m=2 \) 时，隶属度更平滑）。 - $m$ ：模糊因子，控制聚类的模糊程度( $m$ =2 \) 时，隶属度更平滑）。
时间复杂度： 时间复杂度：
计算单个隶属度需要$O(K)$ 的(遍历所有 \($l=1,\dots,K$\)\) 计算单个隶属度需要$O(K)$ 的(遍历所有 \($l=1,\dots,K$\)\)
@ -279,7 +279,7 @@ $$
**3. 更新簇中心** **3. 更新簇中心**
对于每个簇 \( k \)，计算新的簇中心 \( $c_k$ \)： 对于每个簇 $k$ ，计算新的簇中心 $c_k$ ：
$$ $$
c_k = \frac{\sum_{i,j} [\mu_k(a_{ij})]^m a_{ij}}{\sum_{i,j} [\mu_k(a_{ij})]^m} c_k = \frac{\sum_{i,j} [\mu_k(a_{ij})]^m a_{ij}}{\sum_{i,j} [\mu_k(a_{ij})]^m}
$$ $$
@ -299,7 +299,7 @@ $$
**具体矩阵例子** **具体矩阵例子**
假设有一个3×3的邻接矩阵 \( A \)： 假设有一个$3×3$的邻接矩阵 \( A \)：
$$ $$
A = \begin{bmatrix} A = \begin{bmatrix}
0.1 & 0.9 & 0.3 \\ 0.1 & 0.9 & 0.3 \\
@ -307,7 +307,7 @@ A = \begin{bmatrix}
0.4 & 0.6 & 0.5 \\ 0.4 & 0.6 & 0.5 \\
\end{bmatrix} \end{bmatrix}
$$ $$
目标是将矩阵元素聚类为2个簇（\( K=2 \)），分别表示“连接”（簇1）和“断开”（簇2）。 目标是将矩阵元素聚类为2个簇( $K=2$ ），分别表示“连接”（簇1）和“断开”（簇2）。
**步骤1：初始化** **步骤1：初始化**
@ -316,7 +316,7 @@ $$
c_1 = 0.2, \quad c_2 = 0.8 c_1 = 0.2, \quad c_2 = 0.8
$$ $$
- 随机初始化隶属度矩阵 \( U \)（每行和为1）： - 随机初始化隶属度矩阵 $U$（每行和为1）：
$$ $$
U = \begin{bmatrix} U = \begin{bmatrix}
0.6 & 0.4 \\ 0.6 & 0.4 \\
@ -418,7 +418,7 @@ $$
**初始化步骤** **初始化步骤**
- 初始化簇中心和隶属度矩阵 $U$：需要 $O(nK)$ - 初始化簇中心和隶属度矩阵 $U$：需要为每个数据点生成 $K$ 个隶属度值，需要 $O(nK)$
**更新隶属度** **更新隶属度**
@ -463,15 +463,18 @@ $$
### 网络重构 ### 网络重构
对称非负矩阵分解（SNMF）来构造网络的**低维嵌入**表示，从而实现对高维网络邻接矩阵的精确重构。 对称非负矩阵分解（SNMF）要求输入矩阵 $A$ 是**对称且非负**的，分解之后的矩阵 $U$ 是非负的。
低维指的是分解后的$U$矩阵维度小->秩小->重构后的矩阵秩也小。
$$ $$
A \approx U U^T. A \approx U U^T.
$$ $$
对称非负矩阵分解来构造网络的**低维嵌入**表示，从而实现对高维网络邻接矩阵的精确重构。
低维指的是分解后的 $U$ 矩阵维度小->秩小->重构后的矩阵秩也小。
只需计算 $U U^T$ 就能重构出 $A$ 的**低秩**近似版本。如果选择保留全部特征（即 $r = n$），则可以精确还原 $A$；如果只取部分（$r < n$），那么重构结果就是 $A$ 的低秩近似。 只需计算 $U U^T$ 就能重构出 $A$ 的**低秩**近似版本。如果选择保留全部特征（即 $r = n$），则可以精确还原 $A$；如果只取部分（$r < n$），那么重构结果就是 $A$ 的低秩近似。
#### 节点移动模型 #### 节点移动模型
**模拟随机网络中节点的移动方式**，进而间接模拟网络拓扑在不同时刻的变化。它们是用来在仿真环境下产生“网络结构随时间动态变化”的数据，从而让后续的网络重构或网络分析算法有一个逼近真实场景的测试环境。 **模拟随机网络中节点的移动方式**，进而间接模拟网络拓扑在不同时刻的变化。它们是用来在仿真环境下产生“网络结构随时间动态变化”的数据，从而让后续的网络重构或网络分析算法有一个逼近真实场景的测试环境。
@ -522,6 +525,42 @@ $$
2. 不断“旋转” $B$（乘以酉矩阵 $Q$）并对负值做截断，从而让最终的 $U$ 既接近 $B$ 又满足非负性。 2. 不断“旋转” $B$（乘以酉矩阵 $Q$）并对负值做截断，从而让最终的 $U$ 既接近 $B$ 又满足非负性。
这相当于把一部分“逼近”工作用特征分解先做了，然后只用旋转矩阵 $Q$ 来调整局部负值，再配合 $\max(0,\cdot)$ 截断满足非负约束。 这相当于把一部分“逼近”工作用特征分解先做了，然后只用旋转矩阵 $Q$ 来调整局部负值，再配合 $\max(0,\cdot)$ 截断满足非负约束。
**矩阵分解的重构算法步骤为：**
1. **输入**
- 预测特征向量矩阵 $X$
- 特征值矩阵 $\Lambda$
2. **初始化**
$$
B = X \Lambda^{\frac{1}{2}}, \quad Q = I, \quad U = \text{rand}(n, r)
$$
3. **交替更新 $U$, $Q$**
$$
U = \max\bigl(0, B Q\bigr)
$$
4. **继续更新 $Q$**
$$
F = U^T B \quad \Rightarrow \quad [H, \Sigma, V] = \text{svd}(F), \quad Q = V H^T
$$
5. **重复步骤 3、4，直到满足迭代停止条件**
$$
\|U^T(U - BQ)\|_F^2 \le \varepsilon
$$
6. **令**
$$
A' = U U^T
$$
并通过后续 FCM 算法进行聚类
7. **输出嵌入矩阵**
假设我们有一个 $2 \times 2$ 对称非负矩阵 假设我们有一个 $2 \times 2$ 对称非负矩阵
@ -632,6 +671,16 @@ $$
#### 疑问
郭和颜的论文都说满足低秩或者具有低秩性条件的矩阵，SNMF分解出的矩阵是唯一的。可能指的是经过特定算法，输入固定，输出也是固定的。
但是：
- **旋转自由度**：若 $(U, U^T)$ 是一个解，则对任意正交矩阵 $R$（满足 $RR^T=I$），$(UR, R^TU^T)$ 也是有效解。
#### **时间复杂度分析** #### **时间复杂度分析**
(1) 初始构造阶段（假设特征值 特征向量已提前获取，不做分析） (1) 初始构造阶段（假设特征值 特征向量已提前获取，不做分析）

120
科研/颜佳佳论文.md
View File

@ -4,19 +4,127 @@
**直接SNMF分解（无优化）** **直接SNMF分解（无优化）**
- **输入矩阵**：原始动态网络邻接矩阵 $A$（可能稠密或高秩） - 输入矩阵：原始动态网络邻接矩阵 $A$（可能稠密或高秩）
- **处理流程**： - 处理流程：
- 直接对称非负矩阵分解：$A \approx UU^T$ - 直接对称非负矩阵分解：$A \approx UU^T$
- 通过迭代调整$U$和旋转矩阵$Q$逼近目标 - 通过迭代调整$U$和旋转矩阵$Q$逼近目标
- **存在问题**： - 存在问题：
- 高秩矩阵需要保留更多特征值（$\kappa$较大） - 高秩矩阵需要保留更多特征值（$\kappa$较大）
- **非稀疏矩阵计算效率低** - 非稀疏矩阵计算效率低
**先优化再SNMF（论文方法）** **先优化再SNMF（论文方法）**
- **优化阶段**（ADMM）： - 优化阶段（ADMM）：
- 目标函数：$\min_{A_{\text{opt}}} (1-\alpha)\|A_{\text{opt}}\|_* + \alpha\|A_{\text{opt}}\|_1$ - 目标函数：$\min_{A_{\text{opt}}} (1-\alpha)\|A_{\text{opt}}\|_* + \alpha\|A_{\text{opt}}\|_1$
- 输出优化矩阵$A_{\text{opt}}$ - 输出优化矩阵$A_{\text{opt}}$
- **SNMF阶段**： - SNMF阶段：
- 输入变为优化后的$A_{\text{opt}}$ - 输入变为优化后的$A_{\text{opt}}$
- 保持相同分解流程但效率更高 - 保持相同分解流程但效率更高
#### 网络优化中的邻接矩阵重构问题建模与优化
**可行解集合定义（公式4-4）**
$$
\Omega = \left\{ A \middle| A^T = A,\, A \odot P = A_{\text{pre}} \odot P,\, A \odot A_{\max}' = 0 \right\}
$$
- **$A^T = A$**：确保邻接矩阵对称
- **$A \odot P = A_{\text{pre}} \odot P$**：掩码矩阵$P$ ，指定位置的原始值（$\odot$为Hadamard积）
- **$A \odot A_{\max}' = 0$**：功率约束矩阵$\ A_{\max}'$ 禁止在原本无连接的节点间新增边
**限制矩阵$A_{\max}'$的定义（公式4-5）**
$$
A'_{\max, ij} =
\begin{cases}
0, & \text{若 } A_{\max, ij} \ne 0 \\
1, & \text{若 } A_{\max, ij} = 0
\end{cases}
$$
- 通过$A_{\max}'$​标记禁止修改的零元素位置
**原始优化目标（公式4-6）**
$$
\min_{A} \, (1-\alpha)\, \text{rank}(A) + \alpha \|A\|_0
$$
$\|A\|_0$ 表示矩阵 $A$ 中非零元素的个数
- **目标**：平衡低秩性（$\text{rank}(A)$）与稀疏性（$\|A\|_0$）
- **问题**：非凸、不可导，难以直接优化
**凸松弛后的目标（公式4-7）**
$$
\min_{A} \, (1-\alpha)\, \|A\|_* + \alpha \|A\|_1
$$
- **核范数$\|A\|_*$**：奇异值之和，替代$\text{rank}(A)$
- **L1范数$\|A\|_1$**：元素绝对值和，替代$\|A\|_0$
- **性质**：凸优化问题，存在全局最优解
**求解方法**
- **传统方法**：
可转化为**半定规划（SDP）**问题，使用内点法等求解器。但缺点是计算效率低，尤其当矩阵规模大（如多智能体网络节点数 $n$ 很大）时不可行。
- **改进方法**：
采用**ADMM（交替方向乘子法）**结合**投影**和**对偶上升**的方法，适用于动态网络（矩阵频繁变化的情况）。
#### ADMM核心算法
##### **变量定义与作用**
- **输入变量**：
- $A_{pre}$：初始邻接矩阵（优化前的网络拓扑）。
- $P$：对称的0-1矩阵，用于标记 $A_{pre}$ 中非零元素的位置（保持已有边不变）。
- $A'_{max}$：功率最大时的邻接矩阵的补集（$A'_{maxij} = 1$ 表示 $A_{maxij} = 0$，即不允许新增边）。
- $\alpha$：权衡稀疏性（$L_1$ 范数）和低秩性（核范数）的系数。
- **iters**：ADMM迭代次数。
<img src="https://pic.bitday.top/i/2025/04/03/ouy27i-0.png" alt="image-20250403150317427" style="zoom:80%;" />
##### **算法步骤详解**
**(S.1) 更新原始变量 $A$（对应ADMM的$x$步）**
- **代码行4-17**：通过内层循环（投影和对偶上升）更新 $A$。
- **行4-11**：将 $A$ 投影到约束 $A \odot P = A_{\text{pre}} \odot P$ 的集合。
- 通过内层循环（行8-11）迭代更新 $R$，本质是**梯度投影法**：
- $temp_R^{k+1} = M - X^k \odot A_{\text{pre}}$（计算残差）。
- $X^{k+1} = X^k + \beta(A_{\text{pre}} \odot temp_R^{k+1})$（梯度上升步，$\beta$ 为步长）。
- **本质**：通过迭代强制 $A$ 在 $P$ 标记的位置与 $A_{pre}$ 一致。
- **行13-17**：将 $A$ 投影到 $A \odot A'_{\text{max}} = 0$ 的集合。
- 类似地，通过内层循环（行14-17）更新 $Y$：
- $temp_A^{k+1} = D_2 - Y^k \odot A'_{\text{max}}$（残差计算）。
- $Y^{k+1} = Y^k + \gamma(A'_{\text{max}} \odot temp_A^{k+1})$（对偶变量更新）。
**(S.2) 更新辅助变量 $Z_1, Z_2$（对应ADMM的$z$步）**
通过阈值操作分离目标函数的两部分：
- **行18-19**：分别对核范数和 $L_1$ 范数进行阈值操作：
- $Z_1^{t+1} = T_r(A^{t+1} + U_1^t)$：
$T_r(\cdot)$ 是**奇异值阈值算子**（核范数投影），对$A + U1$ 做SVD分解，保留前 $r$ 个奇异值。**作用**：把自己变成低秩矩阵=》强制 $A$ 低秩。
- $Z_2^{t+1} = S_{\alpha}(A^{t+1} + U_2^t)$：
$S_{\alpha}(\cdot)$ 是**软阈值算子**（$L_1$ 范数投影），将小于 $\alpha$ 的元素置零。把自己变成稀疏矩阵=》促进 $A$ 的稀疏性。
**(S.3) 更新 拉格朗日乘子$U_1, U_2$（对应ADMM的对偶上升）**
- **行20-21**：通过残差 $(A - Z)$ 调整拉格朗日乘子 $U_1, U_2$：
- $U_1^{t+1} = U_1^t + A^{t+1} - Z_1^{t+1}$（核范数约束的乘子更新）。
- $U_2^{t+1} = U_2^t + A^{t+1} - Z_2^{t+1}$（$L_1$ 范数约束的乘子更新）。
- **作用**：惩罚 $A$ 与辅助变量 $Z1, Z2$ 的偏差（迫使$A$更贴近$Z$），推动收敛。

18
自学/JavaWeb——后端.md
View File

@ -1222,6 +1222,24 @@ public class SpringbootWebConfig2Application {
} }
``` ```
还可以设置默认值
```java
@RequestMapping("/greet")
public String greet(@RequestParam(defaultValue = "Guest") String name) {
return "Hello, " + name;
}
```
如果既改请求参数名字，又要设置默认值
```java
@RequestMapping("/greet")
public String greet(@RequestParam(value = "age", defaultValue = "25") int userAge) {
return "Age: " + userAge;
}
```
5. 控制反转与依赖注入： 5. 控制反转与依赖注入：

187
自学/力扣Hot 100题.md
View File

@ -351,7 +351,7 @@ public class PriorityQueueExample {
自己实现大根堆： **自己实现大根堆：**
```java ```java
class Solution { class Solution {
@ -566,6 +566,14 @@ public class ArrayExample {
} }
``` ```
复制数组：
```
int[] source = {1, 2, 3, 4, 5};
int[] destination = Arrays.copyOf(source, source.length);
int[] partialArray = Arrays.copyOfRange(source, 1, 4); //不包括索引4
```
#### `二维数组` #### `二维数组`
@ -769,6 +777,183 @@ public class Main {
求最大值：O(n) 求最大值：O(n)
#### 快速排序
**基本思想：**
快速排序是一种基于“分治”思想的排序算法，通过选定一个“枢轴元素（pivot）”，将数组划分为左右两个子区间：左边都小于等于 pivot，右边都大于等于 pivot；然后对这两个子区间递归排序，最终使整个数组有序。
```java
public class QuickSortWithSwap {
// 交换数组中两个元素的位置
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
private static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pivotPos = partition(arr, low, high); // 划分
quickSort(arr, low, pivotPos - 1); // 递归排序左子表
quickSort(arr, pivotPos + 1, high); // 递归排序右子表
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[low]; // 选取第一个元素作为枢轴
int left = low; // 左指针
int right = high; // 右指针
while (left < right) {
// 从右向左找第一个小于枢轴的元素
while (left < right && arr[right] >= pivot) {
right--;
}
// 从左向右找第一个大于枢轴的元素
while (left < right && arr[left] <= pivot) {
left++;
}
// 交换这两个元素
if (left < right) {
swap(arr, left, right);
}
}
// 将枢轴放到最终位置
swap(arr, low, left);
return left; // 返回枢轴的位置
}
public static void main(String[] args) {
int[] arr = {49, 38, 65, 97, 76, 13, 27, 49};
quickSort(arr, 0, arr.length - 1);
System.out.println("\n排序后:");
for (int num : arr) {
System.out.print(num + " ");
}
}
}
```
#### 冒泡排序
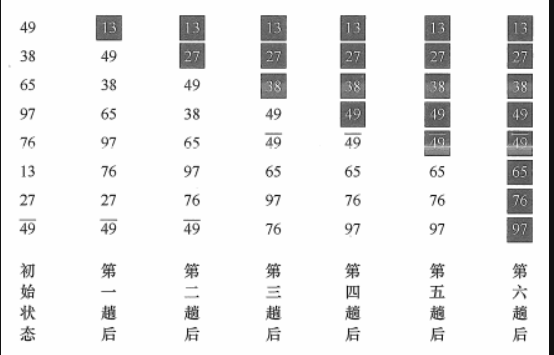
**基本思想：**
【每次将最小/大元素，通过依次交换顺序，放到首/尾位。】
- 从后往前（或从前往后）两两比较相邻元素的值，若为逆序, 则交换它们，直到序列比较完。我们称它为第一趟冒泡，结果是将最小的元素交换到待排序列的第一个位置（或将最大的元素交换到待排序列的最后一个位置）；
- 下一趟冒泡时，前一趟确定的最小元素不再参与比较，每趟冒泡的结果是把序列中的最小元素（或最大元素）放到了序列的最终位置。
- ……这样最多做n - 1趟冒泡就能把所有元素排好序。
- 如若有一趟没有元素交换位置，则可提前说明已排好序。
![image-20250403170049551](https://pic.bitday.top/i/2025/04/03/s4ffs8-0.png)
```java
public void bubbleSort(int[] arr){
//n-1 趟冒泡
for (int i = 0; i < arr.length-1; i++) {
boolean flag=false;
//冒泡
for (int j = arr.length-1; j >i ; j--) {
if (arr[j-1]>arr[j]){
swap(arr,j-1,j);
flag=true;
}
}
//本趟遍历后没有发生交换，说明表已经有序
if (!flag){
return;
}
}
}
private void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
```
#### 归并排序
**基本思想：**
将待排序的数组视为多个有序子表，每个子表的长度为 1，通过两两归并逐步合并成一个有序数组。
**实现思路**
- 分解：递归地将数组拆分成两个子数组，直到每个子数组只有一个元素。
- 合并：将两个有序子数组合并为一个有序数组。
**时间复杂度**：
O(n log n)，无论最坏、最好、平均情况。
```java
public class MergeSort {
/**
* 归并排序（入口函数）
* @param arr 待排序数组
*/
public static void mergeSort(int[] arr) {
if (arr == null || arr.length <= 1) {
return; // 边界条件
}
int[] temp = new int[arr.length]; // 辅助数组
mergeSort(arr, 0, arr.length - 1, temp);
}
private static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (right + left) / 2;
mergeSort(arr, left, mid, temp); // 递归左子数组
mergeSort(arr, mid + 1, right, temp); // 递归右子数组
merge(arr, left, mid, right, temp); // 合并两个有序子数组
}
}
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 左子数组起始指针
int j = mid + 1; // 右子数组起始指针
int t = 0; // 辅助数组指针
// 1. 按序合并两个子数组到temp
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) { // 注意等号保证稳定性
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
// 2. 将剩余元素拷贝到temp
while (i <= mid) {
temp[t++] = arr[i++];
}
while (j <= right) {
temp[t++] = arr[j++];
}
// 3. 将temp中的数据复制回原数组
t = 0;
while (left <= right) {
arr[left++] = temp[t++];
}
}
}
```
#### **数组排序** #### **数组排序**
```java ```java

8
自学/草稿.md
View File

@ -1,6 +1,6 @@
# ConcurrentHashMap 不同JDK版本的实现对比 ConcurrentHashMap 不同JDK版本的实现对比
## 1. 数据结构 1. 数据结构
- **JDK1.7**： - **JDK1.7**：
- 使用 `Segment（分段锁） + HashEntry数组 + 链表` 的数据结构 - 使用 `Segment（分段锁） + HashEntry数组 + 链表` 的数据结构
@ -8,7 +8,7 @@
- **JDK1.8及之后**： - **JDK1.8及之后**：
- 使用 `数组 + 链表/红黑树` 的数据结构（与HashMap类似） - 使用 `数组 + 链表/红黑树` 的数据结构（与HashMap类似）
## 2. 锁的类型与宽度 2. 锁的类型与宽度
- **JDK1.7**： - **JDK1.7**：
- 分段锁(Segment)继承了 `ReentrantLock` - 分段锁(Segment)继承了 `ReentrantLock`
@ -19,7 +19,7 @@
- 空节点：通过CAS添加 - 空节点：通过CAS添加
- 非空节点：通过synchronized加锁 - 非空节点：通过synchronized加锁
## 3. 渐进式扩容（JDK1.8+） 3. 渐进式扩容（JDK1.8+）
- **触发条件**：元素数量 ≥ `数组容量 × 负载因子(默认0.75)` - **触发条件**：元素数量 ≥ `数组容量 × 负载因子(默认0.75)`
- **扩容过程**： - **扩容过程**：