Commit on 2025/05/26 周一 20:59:46.50
152
科研/ZY网络重构分析.md
@ -110,10 +110,124 @@ $$
|
||||
| **输出性质** | 特征值($\lambda_i$)可能是复数 | 奇异值($\sigma_i$)始终为非负实数 |
|
||||
| **正交性** | 仅当 $A$ 正规时 $P$ 是酉矩阵 | $U$ 和 $V$ 始终是酉矩阵(正交) |
|
||||
|
||||
谱分解的对象为实对称矩阵,
|
||||
谱分解的对象为实对称矩阵
|
||||
|
||||
|
||||
|
||||
## 奇异值分解
|
||||
|
||||
### 步骤
|
||||
|
||||
**步骤 1:验证矩阵对称性**
|
||||
|
||||
确保 $A$ 是实对称矩阵(即 $A = A^\top$),此时SVD可通过特征分解直接构造。
|
||||
|
||||
---
|
||||
|
||||
**步骤 2:计算特征分解**
|
||||
|
||||
对 $A$ 进行特征分解:
|
||||
$$
|
||||
A = Q \Lambda Q^\top
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $Q$ 是正交矩阵($Q^\top Q = I$),列向量为 $A$ 的特征向量。
|
||||
- $\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$,$\lambda_i$ 为 $A$ 的特征值(可能有正、负或零)。
|
||||
|
||||
---
|
||||
|
||||
**步骤 3:构造奇异值矩阵 $\Sigma$**
|
||||
|
||||
- **奇异值**:取特征值的绝对值 $\sigma_i = |\lambda_i|$,得到对角矩阵:
|
||||
$$
|
||||
\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_n)
|
||||
$$
|
||||
|
||||
- **排列顺序**:通常按 $\sigma_i$ 降序排列(可选,但推荐)。
|
||||
|
||||
---
|
||||
|
||||
**步骤 4:处理符号(负特征值)**
|
||||
|
||||
- **符号矩阵 $S$**:定义对角矩阵 $S = \text{diag}(s_1, s_2, \dots, s_n)$,其中:
|
||||
$$
|
||||
s_i = \begin{cases}
|
||||
1 & \text{if } \lambda_i \geq 0, \\
|
||||
-1 & \text{if } \lambda_i < 0.
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
- **左奇异向量矩阵 $U$**:调整特征向量的方向:
|
||||
$$
|
||||
U = Q S
|
||||
$$
|
||||
即 $U$ 的列为 $Q$ 的列乘以对应特征值的符号。
|
||||
|
||||
---
|
||||
|
||||
**步骤 5:确定右奇异向量矩阵 $V$**
|
||||
|
||||
由于 $A$ 对称,右奇异向量矩阵 $V$ 直接取特征向量矩阵:
|
||||
$$
|
||||
V = Q
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
**步骤 6:组合得到SVD**
|
||||
|
||||
最终SVD形式为:
|
||||
$$
|
||||
A = U \Sigma V^\top
|
||||
$$
|
||||
验证:
|
||||
$$
|
||||
U \Sigma V^\top = (Q S) \Sigma Q^\top = Q (S \Sigma) Q^\top = Q \Lambda Q^\top = A
|
||||
$$
|
||||
(因为 $S \Sigma = \Lambda$,例如 $\text{diag}(-1) \cdot \text{diag}(2) = \text{diag}(-2)$)。
|
||||
|
||||
### **例子(含正、负、零特征值)**
|
||||
|
||||
设对称矩阵
|
||||
$$
|
||||
A = \begin{bmatrix} 1 & 0 & 2 \\ 0 & -1 & 0 \\ 2 & 0 & 1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
1. **特征分解**
|
||||
|
||||
- 特征值:
|
||||
$$ \lambda_1 = 3, \quad \lambda_2 = -1, \quad \lambda_3 = 0 $$
|
||||
|
||||
- 特征向量矩阵:
|
||||
$$
|
||||
Q = \begin{bmatrix}
|
||||
\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\
|
||||
0 & 1 & 0 \\
|
||||
\frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}}
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
2. **构造SVD**
|
||||
|
||||
- 步骤:
|
||||
1. 按 $|\lambda_i|$ 降序排列:$3, 1, 0$(取绝对值后排序)。
|
||||
2. 奇异值矩阵:
|
||||
$$ \Sigma = \text{diag}(3, 1, 0) $$
|
||||
3. 符号调整矩阵:
|
||||
$$ S = \text{diag}(1, -1, 1) \quad (\lambda_3=0 \text{ 的符号可任选}) $$
|
||||
4. 左奇异向量矩阵:
|
||||
$$ U = Q S = \begin{bmatrix}
|
||||
\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\
|
||||
0 & -1 & 0 \\
|
||||
\frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}}
|
||||
\end{bmatrix} $$
|
||||
5. 右奇异向量矩阵:
|
||||
$$ V = Q $$
|
||||
|
||||
- **验证**:
|
||||
$$ U \Sigma V^\top = A $$
|
||||
|
||||
|
||||
|
||||
## 网络重构分析
|
||||
@ -531,9 +645,37 @@ while low < high:
|
||||
|
||||
|
||||
|
||||
奇异值分解
|
||||
如果量化阈值不一样,你需要**预先**知道矩阵的某个元素$|(A - A_\kappa)_{ij}|$的真实值属于哪个类别(1、4、10),以给元素误差不同的量化阈值,而不是默认的 $d_{\min}$
|
||||
$$
|
||||
\text{误差矩阵: } A - A_\kappa = \left( A - \widetilde{A} \right) + \left( \widetilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
而且不能进行放缩:
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)
|
||||
$$
|
||||
这个式子会导致误差矩阵每个位置的元素取了同样的上界(即都有同样的误差),不能体现真实的误差。
|
||||
|
||||
|
||||
|
||||
方法一:
|
||||
|
||||
实验法,选取若干组数据做实验,
|
||||
|
||||
数据包括真实矩阵 $A$ 和重构矩阵 $A_\kappa$ ,选取不同的 $\kappa$ 值计算误差矩阵 $E(\kappa)$ ,根据真实矩阵A,预先知道$E(\kappa)$ 每个位置的量化阈值,若每个位置$E(\kappa)$ 都小于其的量化阈值,那么当前的 $\kappa$ 符合条件。
|
||||
|
||||
|
||||
|
||||
方法二:
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right) \leq \min_{1\le m\le K-1} d_m.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
量化误差
|
||||
|
||||

|
||||
|
||||
@ -541,6 +683,10 @@ while low < high:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
滤波误差:
|
||||
|
||||
高飞、李镇和都是**实验统计**误差加和获取 + 幂律分布和线性分布 精度预估??
|
||||
|
||||
600
科研/草稿.md
@ -1,545 +1,91 @@
|
||||
如何确定kmeans的簇数?节点之间的流量,空间转为时间的图。
|
||||
|
||||
压缩感知 函数拟合 采样定理 傅里叶变换
|
||||
|
||||
|
||||
|
||||
## **谱分解**与网络重构
|
||||
|
||||
实对称矩阵性质:
|
||||
|
||||
对于任意 $n \times n$ 的实对称矩阵 $A$:
|
||||
|
||||
1. **秩可以小于 $n$**(即存在零特征值,矩阵不可逆)。
|
||||
|
||||
2. 但仍然有 $n$ 个线性无关的特征向量(即可对角化)。
|
||||
|
||||
3. 特征值有正有负!!!
|
||||
|
||||
|
||||
|
||||
一个实对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的**对称矩阵** $A$,
|
||||
|
||||
**完整谱分解**可以表示为:
|
||||
$$
|
||||
A = Q \Lambda Q^T \\
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
$Q$是$n \times n$的正交矩阵,每一列是一个特征向量;$\Lambda$是$n \times n$的对角矩阵,对角线元素是特征值$\lambda_i$ ,其余为0。
|
||||
|
||||
其中,$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值,$x_i$ 是对应的特征向量。**(注意!这里的特征向量需要归一化!!!)**
|
||||
|
||||
|
||||
|
||||
**如果矩阵 $A$ 的秩为 $r$ ,那么谱分解里恰好有 $r$ 个非零特征值。**
|
||||
|
||||
用这 $r$ 对特征值/特征向量就能**精确**重构出 $A$,因为零特征值对矩阵重构不提供任何贡献。
|
||||
|
||||
因此,需要先对所有特征值取绝对值,从大到小排序,取前 $r$ 个!!!
|
||||
|
||||
|
||||
|
||||
**截断的谱分解**(取前 $\kappa$ 个特征值和特征向量)
|
||||
|
||||
如果我们只保留前 $\kappa$ 个绝对值最大的特征值和对应的特征向量,那么:
|
||||
|
||||
- **特征向量矩阵 $U_\kappa$**:取 $U$ 的前 $\kappa$ 列,维度为 $n \times \kappa$。
|
||||
- **特征值矩阵 $\Lambda_\kappa$**:取 $\Lambda$ 的前 $\kappa \times \kappa$ 子矩阵(即前 $\kappa$ 个对角线元素),维度为 $\kappa \times \kappa$。
|
||||
|
||||
因此,截断后的近似分解为:
|
||||
|
||||
$$
|
||||
A \approx U_\kappa \Lambda_\kappa U_\kappa^T\\
|
||||
A \approx \sum_{i=1}^{\kappa} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
**推导过程**
|
||||
|
||||
1. **特征值和特征向量的定义**
|
||||
对于一个对称矩阵 $A$,其特征值和特征向量满足:
|
||||
|
||||
$$
|
||||
A x_i = \lambda_i x_i
|
||||
$$
|
||||
|
||||
其中,$\lambda_i$ 是特征值,$x_i$ 是对应的特征向量。
|
||||
|
||||
2. **谱分解**
|
||||
将这些特征向量组成一个正交矩阵 $Q$
|
||||
|
||||
$A = Q \Lambda Q^T$
|
||||
|
||||
$$
|
||||
Q = \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix},
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix}.
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda Q^T = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_n^T \end{bmatrix}.
|
||||
$$
|
||||
|
||||
$$
|
||||
Q \Lambda Q^T = \lambda_1 x_1 x_1^T + \lambda_2 x_2 x_2^T + \cdots + \lambda_n x_n x_n^T.
|
||||
$$
|
||||
|
||||
可以写为
|
||||
$$
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
3. **网络重构**
|
||||
在随机网络中,网络的邻接矩阵 $A$ 通常是对称的。利用预测算法得到的谱参数 $\{\lambda_i, x_i\}$ 后,就可以用以下公式重构网络矩阵:
|
||||
|
||||
$$
|
||||
A(G) = \sum_{i=1}^{n} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
|
||||
|
||||
| **性质** | **特征分解/谱分解** | **奇异值分解(SVD)** |
|
||||
| ------------ | -------------------------------- | ------------------------------------------ |
|
||||
| **适用矩阵** | 仅限**方阵**($n \times n$) | **任意矩阵**($m \times n$,包括矩形矩阵) |
|
||||
| **分解形式** | $A = P \Lambda P^{-1}$ | $A = U \Sigma V^*$ |
|
||||
| **矩阵类型** | 可对角化矩阵(如对称、正规矩阵) | 所有矩阵(包括不可对角化的方阵和非方阵) |
|
||||
| **输出性质** | 特征值($\lambda_i$)可能是复数 | 奇异值($\sigma_i$)始终为非负实数 |
|
||||
| **正交性** | 仅当 $A$ 正规时 $P$ 是酉矩阵 | $U$ 和 $V$ 始终是酉矩阵(正交) |
|
||||
|
||||
谱分解的对象为实对称矩阵,
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 网络重构分析
|
||||
|
||||
### 基于扰动理论的特征向量估算方法
|
||||
|
||||
设原矩阵为 $A$,扰动后矩阵为 $A+\zeta C$(扰动矩阵 $\zeta C$,$\zeta$是小参数),令其第 $i$ 个特征值、特征向量分别为 $\lambda_i,x_i$ 和 $\tilde\lambda_i,\tilde x_i$。
|
||||
|
||||
**特征向量的一阶扰动公式:**
|
||||
$$
|
||||
\Delta x_i
|
||||
=\tilde x_i - x_i
|
||||
\;\approx\;
|
||||
\zeta \sum_{k\neq i}
|
||||
\frac{x_k^T\,C\,x_i}{\lambda_i - \lambda_k}\;x_k,
|
||||
$$
|
||||
|
||||
- **输出**:对应第 $i$ 个特征向量修正量 $\Delta x_i$。
|
||||
|
||||
|
||||
|
||||
**特征值的一阶扰动公式:**
|
||||
$$
|
||||
\Delta\lambda_i = \tilde\lambda_i - \lambda_i \;\approx\;\zeta\,x_i^T\,C\,x_i
|
||||
$$
|
||||
**关键假设:**当扰动较小( $\zeta\ll1$) 且各模态近似正交均匀时,常作进一步近似
|
||||
$$
|
||||
x_k^T\,C\,x_i \;\approx\; x_i^T\,C\,x_i \;
|
||||
$$
|
||||
正交: $\{x_k\}$ 本身是正交基,这是任何对称矩阵特征向量天然具有的属性。
|
||||
|
||||
均匀:我们把 $C$ 看作“**不偏向任何特定模态**”的随机小扰动——换句话说,投影到任何两个方向 $(x_i,x_k)$ 上的耦合强度 $x_k^T\,C\,x_i\quad\text{和}\quad x_i^T\,C\,x_i$ 在数值量级上应当差不多,因此可以互相近似。
|
||||
|
||||
|
||||
|
||||
因此,将所有的 $x_k^T C x_i$ 替换为 $x_i^T C x_i$:
|
||||
$$
|
||||
\Delta x_i \approx \zeta \sum_{k\neq i} \frac{x_i^T C x_i}{\lambda_i - \lambda_k} x_k = \zeta (x_i^T C x_i) \sum_{k\neq i} \frac{1}{\lambda_i - \lambda_k} x_k = \sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
|
||||
$$
|
||||
|
||||
$$
|
||||
\Delta x_i \approx\sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
|
||||
$$
|
||||
|
||||
问题:
|
||||
|
||||
1. **当前时刻的邻接矩阵**
|
||||
$$
|
||||
A^{(1)}\in\mathbb R^{n\times n},\qquad
|
||||
A^{(1)}\,x_i^{(1)}=\lambda_i^{(1)}\,x_i^{(1)},\quad \|x_i^{(1)}\|=1.
|
||||
$$
|
||||
|
||||
2. **下一时刻的邻接矩阵**
|
||||
$$
|
||||
A^{(2)}\in\mathbb R^{n\times n},
|
||||
$$
|
||||
**已知**它的第 $i$ 个特征值 $\lambda_i^{(2)}$(卡尔曼滤波得来). **求**当前时刻的特征向量 $x_i^{(2)}$。
|
||||
|
||||
|
||||
|
||||
**下一时刻**第 $i$ 个特征向量的预测为
|
||||
$$
|
||||
\boxed{
|
||||
x_i^{(2)}
|
||||
\;=\;
|
||||
x_i^{(1)}+\Delta x_i
|
||||
\;\approx\;
|
||||
x_i^{(1)}
|
||||
+\sum_{k\neq i}
|
||||
\frac{\lambda_i^{(2)}-\lambda_i^{(1)}}
|
||||
{\lambda_i^{(1)}-\lambda_k^{(1)}}\;
|
||||
x_k^{(1)}.
|
||||
}
|
||||
$$
|
||||
通过该估算方法可以依次求出下一时刻的所有特征向量。
|
||||
|
||||
### 矩阵符号说明
|
||||
|
||||
- 原始(真实)邻接矩阵 $A$ ,假设 $A$ 的秩为 $r$: $\lambda_{r+1}=\cdots=\lambda_n=0$
|
||||
$$
|
||||
A = \sum_{m=1}^n \lambda_m\,x_m x_m^T=\begin{align*}
|
||||
\sum_{m=1}^r \lambda_m x_m x_m^T + \sum_{m=r+1}^n \lambda_m x_m x_m^T = \sum_{m=1}^r \lambda_m x_m x_m^T
|
||||
\end{align*},
|
||||
$$
|
||||
|
||||
|
||||
|
||||
- 滤波估计得到的矩阵及谱分解:
|
||||
$$
|
||||
\widetilde A = \sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||||
\quad \widetilde\lambda_1\ge\cdots\ge\widetilde\lambda_n\;
|
||||
$$
|
||||
|
||||
- 只取前 $\kappa$ 项重构 :
|
||||
$$
|
||||
A_\kappa \;=\;\sum_{m=1}^\kappa \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||||
$$
|
||||
|
||||
- 对 $A_\kappa$ 进行K-means聚类,得到 $A_{final}$
|
||||
|
||||
|
||||
|
||||
目标是让 $A_{final}$ = $A$
|
||||
|
||||
|
||||
|
||||
### **0/1矩阵**
|
||||
|
||||
其中 $\widetilde{\lambda}_i$ 和 $\widetilde{x}_i$ 分别为通过预测得到矩阵 $\widetilde A$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差,直接进行矩阵重构会使得重构误差较大。 对于这个问题,文献提出一种 0/1 矩阵近似恢复算法。
|
||||
$$
|
||||
a_{ij} =
|
||||
\begin{cases}
|
||||
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
|
||||
0, & \text{else}
|
||||
\end{cases}
|
||||
$$
|
||||
只要我们的估计值与真实值之间差距**小于 0.5**,就能保证阈值处理以后准确地恢复原边信息。
|
||||
|
||||
|
||||
|
||||
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
|
||||
|
||||
真实矩阵 $A$ 与预测矩阵 $\widetilde{A} $ 之间的差为 (秩为 $r$)
|
||||
$$
|
||||
A - \widetilde{A}=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T
|
||||
$$
|
||||
**若假设特征向量扰动可忽略,即$\widetilde x_m\approx x_m$ ,扰动可简化为(这里可能有问题,特征向量的扰动也要计算)**
|
||||
$$
|
||||
A - \widetilde{A} = \sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
对于任意元素 $(i, j)$ 上有
|
||||
$$
|
||||
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^r \Delta \lambda_m ({x}_m {x}_m^T)_{ij} \right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
于一个归一化的特征向量 ${x}_m$,其外积矩阵$ {x}_m {x}_m^T$ 满足
|
||||
$$
|
||||
|({x}_m {x}_m^T)_{ij}| \leq 1.
|
||||
$$
|
||||
例:
|
||||
$$
|
||||
x_m = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\\
|
||||
x_m x_m^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
||||
$$
|
||||
每个元素的绝对值$\leq1$
|
||||
|
||||
|
||||
$$
|
||||
\left| \sum_{m=1}^r \Delta \lambda_m (x_m x_m^T)_{ij} \right| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m|.
|
||||
$$
|
||||
为了确保 $|a_{ij} - \widetilde{a}_{ij}| < \frac{1}{2}$ 对所有 $(i,j)$ 成立,网络精准重构条件为:
|
||||
$$
|
||||
\sum_{m=1}^r\left| \Delta \lambda_m\right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
||||
|
||||
|
||||
|
||||
如果在**高层次**(特征值滤波)的误差累积超过了一定阈值,就有可能在**低层次**(邻接矩阵元素)中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5,就可以保证0-1矩阵的精确重构。
|
||||
|
||||
|
||||
|
||||
### **非0/1矩阵**
|
||||
|
||||
#### **量化误差**
|
||||
|
||||
对估计矩阵 $\tilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类,得到每个簇中心 $\{c_k\}_{k=1}^K$。
|
||||
|
||||
- **簇内平均偏差**:
|
||||
对于第 $k$簇,算该簇所有点到中心的平均绝对偏差:
|
||||
$$
|
||||
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
|
||||
$$
|
||||
|
||||
- **全局允许误差**:
|
||||
$$
|
||||
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### 对于归一化向量 $x_m$ 的研究
|
||||
|
||||
$$
|
||||
x_m = \begin{bmatrix} x_{m,1} \\ x_{m,2} \\ \vdots \\ x_{m,d} \end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
x_m x_m^T =
|
||||
\begin{bmatrix}
|
||||
x_{m,1}^2 & x_{m,1}x_{m,2} & \cdots & x_{m,1}x_{m,d} \\
|
||||
x_{m,2}x_{m,1} & x_{m,2}^2 & \cdots & x_{m,2}x_{m,d} \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
x_{m,d}x_{m,1} & x_{m,d}x_{m,2} & \cdots & x_{m,d}^2
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
$$
|
||||
(x_m x_m^T)_{ij}=x_{m,i}\,x_{m,j}\,,
|
||||
$$
|
||||
|
||||
**对于任意元素:**由于 $\|x_m\|_2=1$ 且 $|x_{m,i}|\le1$,必有
|
||||
$$
|
||||
|x_{m,i}x_{m,j}|\le1\,.
|
||||
$$
|
||||
|
||||
**对于非对角线元素:**
|
||||
|
||||
对任意 $i\neq j$,由
|
||||
$$
|
||||
x_{m,i}^2 + x_{m,j}^2 \le \sum_{k=1}^d x_{m,k}^2 = 1
|
||||
$$
|
||||
|
||||
$$
|
||||
(|x_{m,i}| - |x_{m,j}|)^2 \geq 0 \implies |x_{m,i}|^2 + |x_{m,j}|^2 \geq 2 |x_{m,i}| |x_{m,j}|.
|
||||
$$
|
||||
|
||||
$$
|
||||
|x_{m,i}x_{m,j}| = |x_{m,i}||x_{m,j}| \leq \frac{|x_{m,i}|^2 + |x_{m,j}|^2}{2} = \frac{x_{m,i}^2 + x_{m,j}^2}{2}.
|
||||
$$
|
||||
|
||||
$$
|
||||
|(x_m x_m^T)_{ij}|=|x_{m,i}x_{m,j}| \le \frac{x_{m,i}^2 + x_{m,j}^2}{2} \le \frac12\,,
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
#### 带权重构需控制两类误差:
|
||||
|
||||
这里暂时忽略特征向量的扰动,即 $x_m=\widetilde x_m$
|
||||
|
||||
1. **滤波误差**$\eta$:
|
||||
|
||||
**来源**:滤波器在谱域对真实特征值/向量的估计偏差,包括
|
||||
|
||||
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
|
||||
- **特征向量:矩阵扰动得来**
|
||||
- 设矩阵 $A$ 的秩为 $r$
|
||||
|
||||
$$
|
||||
A - \widetilde A=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
|
||||
$$
|
||||
\Bigl\|\sum_{m=1}^r \Delta\lambda_m\, x_m x_m^T\Bigr\|_F = \sqrt{\sum_{m=1}^r (\Delta\lambda_m)^2}.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
2. **截断谱分解误差** $\epsilon$:
|
||||
只取前 $\kappa$ 个特征对重构
|
||||
|
||||
$$
|
||||
A_\kappa \;=\;\sum_{m=1}^\kappa \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\;\sum_{m=1}^\kappa \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
$$
|
||||
\widetilde A - A_\kappa=\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
|
||||
$$
|
||||
\Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.\epsilon
|
||||
= \Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
3. **总的误差**
|
||||
$$
|
||||
\text{误差矩阵: } A - A_\kappa = \left( A - \widetilde{A} \right) + \left( \widetilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
|
||||
- 研究单个元素误差:
|
||||
$$
|
||||
\text{元素误差绝对值:}|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m| \cdot |(x_m x_m^T)_{ij}|
|
||||
$$
|
||||
对于非对角线元素,由于 $|(x_m x_m^T)_{ij}| \leq \frac12$(归一化特征向量):
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)
|
||||
$$
|
||||
|
||||
- 研究整个矩阵误差:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \left\| \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \right\|_F^2
|
||||
$$
|
||||
而 $\| x_m x_m^T \|_F = \sqrt{\text{tr}(x_m x_m^T x_m x_m^T)} = \sqrt{\text{tr}(x_m x_m^T)} = \| x_m \|_2 = 1$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2
|
||||
$$
|
||||
最终:
|
||||
$$
|
||||
\| A - A_\kappa \|_F = \sqrt{ \sum_{m=1}^r |\Delta \lambda_m|^2 + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|^2 }
|
||||
$$
|
||||
Here’s the revised content with formulas wrapped in `$` or `$$` for Markdown compatibility:
|
||||
|
||||
---
|
||||
|
||||
4. **最终约束条件**:
|
||||
### **步骤 1:验证矩阵对称性**
|
||||
确保 $A$ 是实对称矩阵(即 $A = A^\top$),此时SVD可通过特征分解直接构造。
|
||||
|
||||
---
|
||||
|
||||
### **步骤 2:计算特征分解**
|
||||
对 $A$ 进行特征分解:
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq 量化阈值\tau
|
||||
A = Q \Lambda Q^\top
|
||||
$$
|
||||
其中:
|
||||
- $Q$ 是正交矩阵($Q^\top Q = I$),列向量为 $A$ 的特征向量。
|
||||
- $\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$,$\lambda_i$ 为 $A$ 的特征值(可能有正、负或零)。
|
||||
|
||||
---
|
||||
|
||||
### **步骤 3:构造奇异值矩阵 $\Sigma$**
|
||||
- **奇异值**:取特征值的绝对值 $\sigma_i = |\lambda_i|$,得到对角矩阵:
|
||||
$$
|
||||
\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_n)
|
||||
$$
|
||||
- **排列顺序**:通常按 $\sigma_i$ 降序排列(可选,但推荐)。
|
||||
|
||||
---
|
||||
|
||||
### **步骤 4:处理符号(负特征值)**
|
||||
- **符号矩阵 $S$**:定义对角矩阵 $S = \text{diag}(s_1, s_2, \dots, s_n)$,其中:
|
||||
$$
|
||||
s_i = \begin{cases}
|
||||
1 & \text{if } \lambda_i \geq 0, \\
|
||||
-1 & \text{if } \lambda_i < 0.
|
||||
\end{cases}
|
||||
$$
|
||||
- **左奇异向量矩阵 $U$**:调整特征向量的方向:
|
||||
$$
|
||||
U = Q S
|
||||
$$
|
||||
即 $U$ 的列为 $Q$ 的列乘以对应特征值的符号。
|
||||
|
||||
---
|
||||
|
||||
### **步骤 5:确定右奇异向量矩阵 $V$**
|
||||
由于 $A$ 对称,右奇异向量矩阵 $V$ 直接取特征向量矩阵:
|
||||
$$
|
||||
V = Q
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### **步骤 6:组合得到SVD**
|
||||
最终SVD形式为:
|
||||
$$
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
A = U \Sigma V^\top
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### 量化阈值推导
|
||||
|
||||
要保证重构矩阵 $A_\kappa$ 在每个位置上“落到”正确的某一 簇而不搞混,就必须让重构误差的最大绝对值严格小于任意两个相邻量化级别之间的半距(half‐spacing)。具体地:
|
||||
|
||||
1. **量化级别及间距定义**
|
||||
设原始矩阵元素只能取 $K$ 个离散值:
|
||||
$$
|
||||
v_1 < v_2 < \cdots < v_K,
|
||||
$$
|
||||
相邻级别间距为:
|
||||
$$
|
||||
d_m = v_{m+1} - v_m,\quad m=1,\dots,K-1.
|
||||
$$
|
||||
|
||||
2. **最小间距确定**
|
||||
计算所有相邻级别的最小间距:
|
||||
$$
|
||||
d_{\min} = \min_{1\le m\le K-1} d_m.
|
||||
$$
|
||||
|
||||
3. **通用误差阈值**
|
||||
为确保重构值不会"越界"到相邻级别,取阈值:
|
||||
$$
|
||||
\boxed{\tau = \frac{d_{\min}}{2}.}
|
||||
$$
|
||||
|
||||
**示例:**
|
||||
|
||||
1. 0-1矩阵,$a=0, b=1,K=2$,量化阈值为0.5。
|
||||
2. 量化级别 $\{0,\,0.3,\,0.7,\,1\}$ ,$K=4$ 时:
|
||||
- 相邻间距:$0.3, 0.4, 0.3$
|
||||
- $d_{\min}=0.3$,故 $\tau=0.15$
|
||||
|
||||
|
||||
|
||||
#### 维数选择推导
|
||||
|
||||
验证:
|
||||
$$
|
||||
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
|
||||
U \Sigma V^\top = (Q S) \Sigma Q^\top = Q (S \Sigma) Q^\top = Q \Lambda Q^\top = A
|
||||
$$
|
||||
(因为 $S \Sigma = \Lambda$,例如 $\text{diag}(-1) \cdot \text{diag}(2) = \text{diag}(-2)$)。
|
||||
|
||||
已知 $\sum_{m=1}^r |\Delta \lambda_m|=\eta$ ,量化阈值 $\tau$ ,令 $s=2\tau-\eta$ ,设截断谱分解误差为 $\epsilon$
|
||||
$$
|
||||
\epsilon \leq 2\tau-\eta
|
||||
$$
|
||||
借助**前缀和+二分查找**寻找最小的 $\kappa$ :
|
||||
---
|
||||
|
||||
1. **预处理:计算前缀和**
|
||||
### **关键性质与注意事项**
|
||||
1. **奇异值与特征值**:$\Sigma$ 的非零对角元是 $|\Lambda|$ 的非零对角元。
|
||||
2. **零特征值**:若 $\lambda_i = 0$,则 $\sigma_i = 0$,对应 $U$ 和 $V$ 的列向量属于 $A$ 的核空间。
|
||||
3. **唯一性**:
|
||||
- 奇异值 $\Sigma$ 唯一(按降序排列时)。
|
||||
- 奇异向量 $U$ 和 $V$ 的符号可能不唯一(因特征向量方向可反转)。
|
||||
4. **计算效率**:对称矩阵的SVD无需计算 $AA^\top$ 或 $A^\top A$,直接通过特征分解获得。
|
||||
|
||||
2. 设绝对值降序的估计特征值列表为 $\bigl|\widetilde\lambda_1\bigr| \ge \bigl|\widetilde\lambda_2\bigr| \ge \cdots \ge \bigl|\widetilde\lambda_r\bigr|$,
|
||||
计算它们的前缀和:
|
||||
$$
|
||||
S_k = \sum_{m=1}^k \bigl|\widetilde\lambda_m\bigr|, \quad k=0,1,\dots,r, \quad S_0=0.
|
||||
$$
|
||||
总和 $S_r = \sum_{m=1}^r \bigl|\widetilde\lambda_m\bigr|$ 对应 $\kappa=0$ 时的最大截断误差。
|
||||
---
|
||||
|
||||
3. **将「尾和 ≤ 预算 $s$」转成前缀和条件**
|
||||
记预算 $s = 2\tau - \eta$,尾部累积(截断误差)为:
|
||||
### **示例**
|
||||
设对称矩阵 $A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$:
|
||||
1. **特征分解**:
|
||||
- 特征值:$\lambda_1 = 1$, $\lambda_2 = -1$。
|
||||
- 特征向量:$Q = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$。
|
||||
2. **构造SVD**:
|
||||
- $\Sigma = \text{diag}(1, 1)$($|\lambda_i|$)。
|
||||
- $S = \text{diag}(1, -1)$,故 $U = Q S = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}$。
|
||||
- $V = Q$。
|
||||
3. **结果**:
|
||||
$$
|
||||
T(k) = \sum_{m=k+1}^r \bigl|\widetilde\lambda_m\bigr| = S_r - S_k.
|
||||
$$
|
||||
条件 $T(k) \le s$ 等价于:
|
||||
$$
|
||||
S_k \ge S_r - s.
|
||||
$$
|
||||
定义阈值:
|
||||
$$
|
||||
\theta = S_r - s.
|
||||
A = \underbrace{\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}}_U \underbrace{\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}}_\Sigma \underbrace{\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}^\top}_{V^\top}
|
||||
$$
|
||||
|
||||
4. **二分查找最小 $\kappa$**
|
||||
在已排好序的数组 $S_k$(严格单调递增或非减)中,用二分查找找出最小的 $k$ 使得
|
||||
$$
|
||||
S_k \;\ge\;\theta.
|
||||
$$
|
||||
此 $k$ 即为所求的最小截断秩 $\kappa$。
|
||||
|
||||
**伪代码:**
|
||||
|
||||
```python
|
||||
# 输入:绝对值降序的估计特征值列表 |λ̃₁| ≥ |λ̃₂| ≥ ... ≥ |λ̃ᵣ|, 预算 s ≥ 0
|
||||
S = [0] * (r+1) # 前缀和数组初始化
|
||||
for k in range(1, r+1):
|
||||
S[k] = S[k-1] + |λ̃ₖ| # 计算前缀和(实际代码中需替换 |λ̃ₖ| 为具体变量)
|
||||
|
||||
θ = S[r] - s # 计算查找阈值
|
||||
|
||||
# 在 S[0..r] 中二分查找最小 k 使得 S[k] ≥ θ
|
||||
low, high = 0, r
|
||||
while low < high:
|
||||
mid = (low + high) // 2
|
||||
if S[mid] < θ:
|
||||
low = mid + 1
|
||||
else:
|
||||
high = mid
|
||||
κ = low # 最终得到的最小截断
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
奇异值分解
|
||||
|
||||
量化误差
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
滤波误差:
|
||||
|
||||
高飞、李镇和都是**实验统计**误差加和获取 + 幂律分布和线性分布 精度预估??
|
||||
---
|
||||
@ -120,7 +120,8 @@ docker image prune
|
||||
|
||||
-p <宿主机端口>:<容器端口> : 将容器内部的端口映射到宿主机,**使外部可以访问容器提供的服务,如果不写的话,只有容器内部网络能访问它**比如mysql,如果写''-p 3307:3306',那么可以用navicat连接localhost:3307访问这个数据库。
|
||||
|
||||
--restart <策略> :设置容器的重启策略,如 `no`(默认不重启)、`on-failure`(失败时重启)、`always`(总是重启)或 `unless-stopped`。
|
||||
--restart <策略> :设置容器的重启策略,如 `no`(默认不重启)、`on-failure`(失败时重启)、`always`(总是重启)或 `unless-stopped`(最重要!docker服务重启时,它也跟着重启)。
|
||||
|
||||
|
||||
-v <宿主机目录>:<容器目录>` 或 `--volume : 如 -v /host/data:/app/data
|
||||
|
||||
|
||||
117
自学/Jmeter快速入门.md
Normal file
@ -0,0 +1,117 @@
|
||||
# Jmeter快速入门
|
||||
|
||||
|
||||
|
||||
# 1.安装Jmeter
|
||||
|
||||
Jmeter依赖于JDK,所以必须确保当前计算机上已经安装了JDK,并且配置了环境变量。
|
||||
|
||||
|
||||
|
||||
## 1.1.下载
|
||||
|
||||
可以Apache Jmeter官网下载,地址:http://jmeter.apache.org/download_jmeter.cgi
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
## 1.2.解压
|
||||
|
||||
因为下载的是zip包,解压缩即可使用,目录结构如下:
|
||||
|
||||
|
||||
|
||||
其中的bin目录就是执行的脚本,其中包含启动脚本:
|
||||
|
||||
|
||||
|
||||
### 1.3.运行
|
||||
|
||||
双击即可运行,但是有两点注意:
|
||||
|
||||
- 启动速度比较慢,要耐心等待
|
||||
- 启动后黑窗口不能关闭,否则Jmeter也跟着关闭了
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
# 2.快速入门
|
||||
|
||||
|
||||
|
||||
## 2.1.设置中文语言
|
||||
|
||||
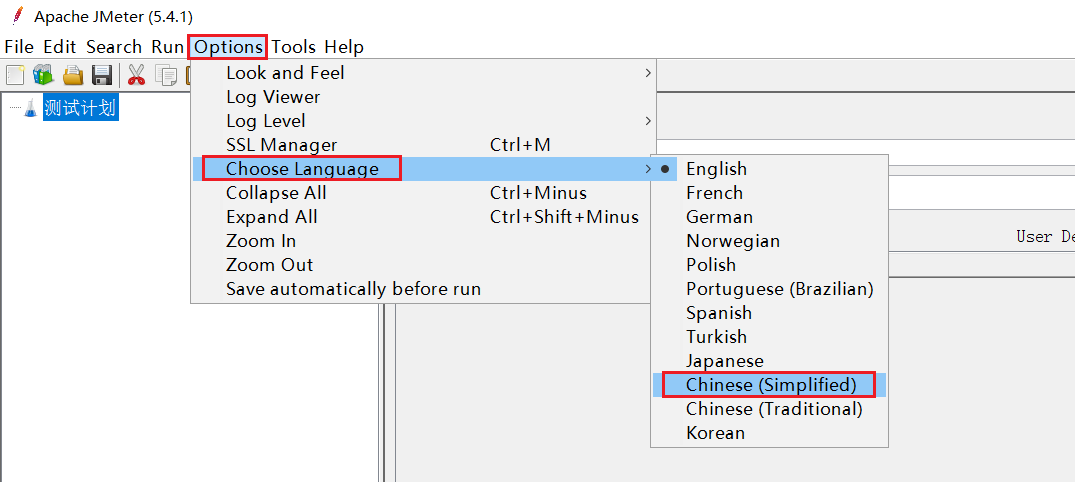
默认Jmeter的语言是英文,需要设置:
|
||||
|
||||
|
||||
|
||||
效果:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
> **注意**:上面的配置只能保证本次运行是中文,如果要永久中文,需要修改Jmeter的配置文件
|
||||
|
||||
|
||||
|
||||
打开jmeter文件夹,在bin目录中找到 **jmeter.properties**,添加下面配置:
|
||||
|
||||
```properties
|
||||
language=zh_CN
|
||||
```
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
> 注意:前面不要出现#,#代表注释,另外这里是下划线,不是中划线
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 2.2.基本用法
|
||||
|
||||
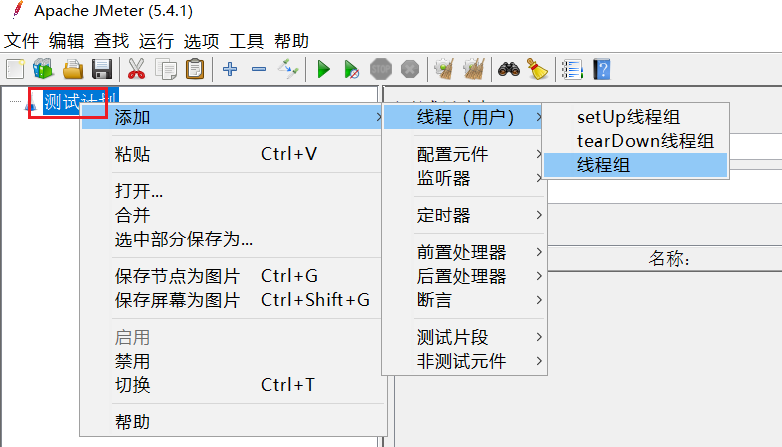
在测试计划上点鼠标右键,选择添加 > 线程(用户) > 线程组:
|
||||
|
||||
|
||||
|
||||
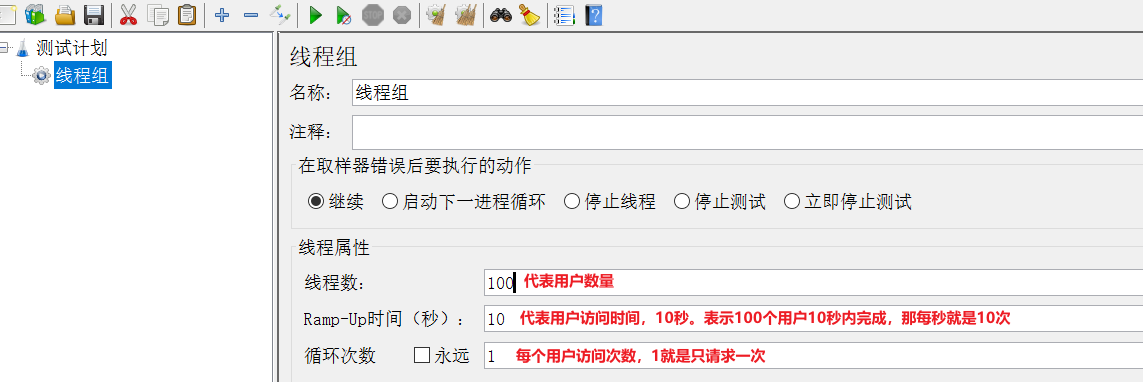
在新增的线程组中,填写线程信息:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
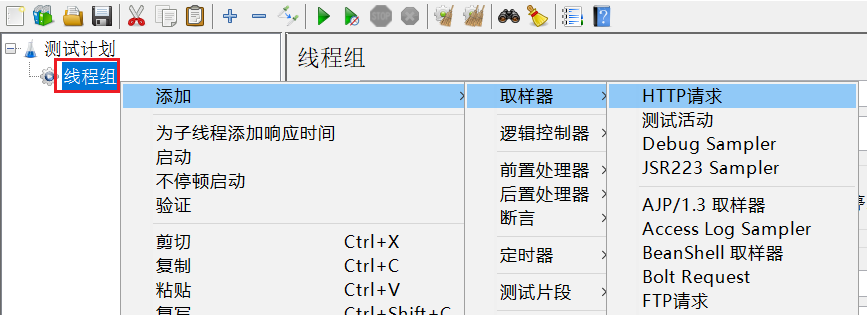
给线程组点鼠标右键,添加http取样器:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
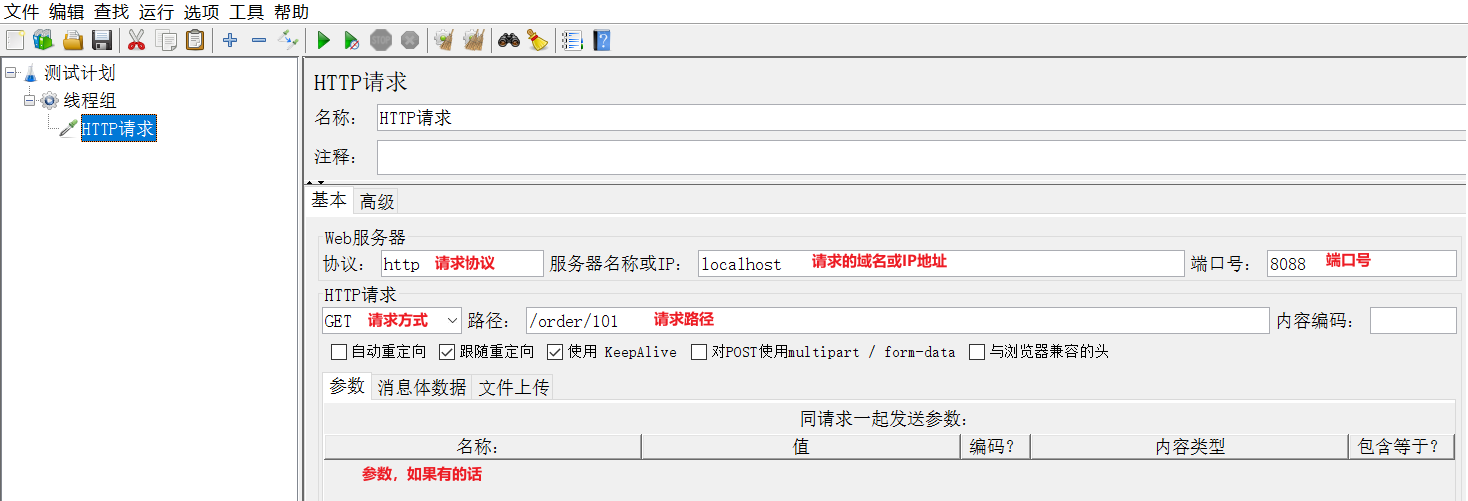
编写取样器内容:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
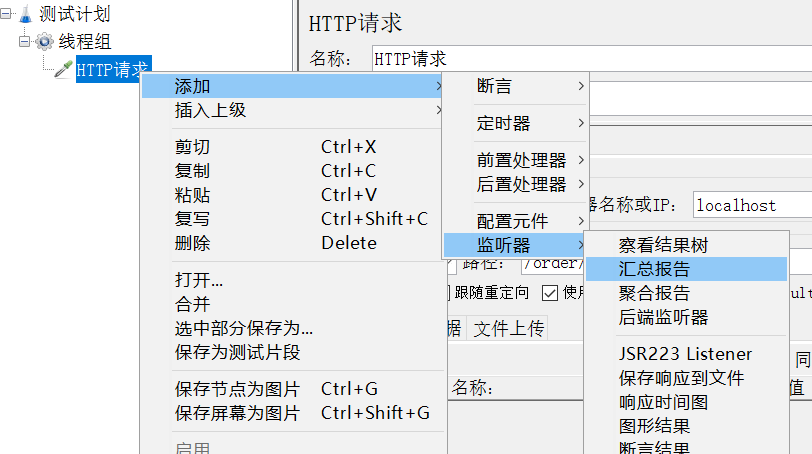
添加监听报告:
|
||||
|
||||
|
||||
|
||||
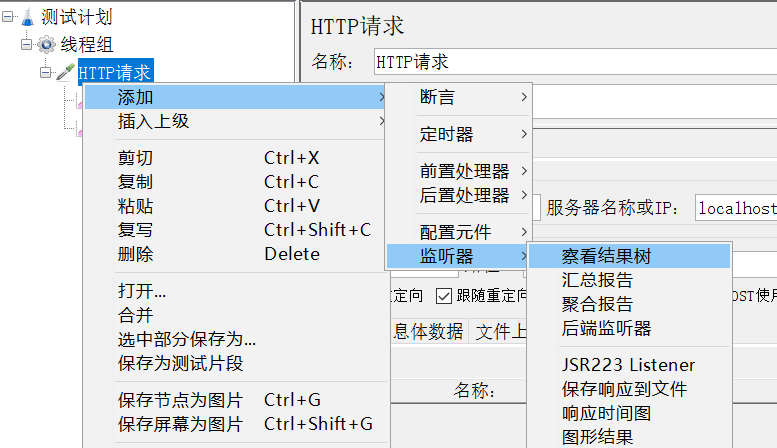
添加监听结果树:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
汇总报告结果:
|
||||
|
||||

|
||||
|
||||
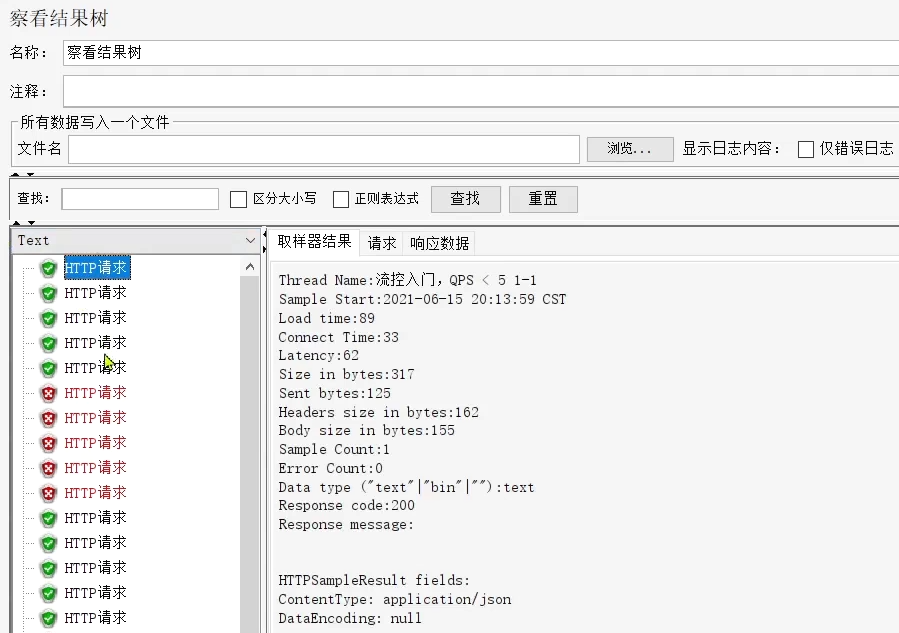
结果树:
|
||||
|
||||
|
||||
|
||||
BIN
自学/assets/image-20210618201340086.png
Normal file
|
After Width: | Height: | Size: 3.7 KiB |
BIN
自学/assets/image-20210618201412878.png
Normal file
|
After Width: | Height: | Size: 59 KiB |
BIN
自学/assets/image-20210618201607831.png
Normal file
|
After Width: | Height: | Size: 72 KiB |
BIN
自学/assets/image-20210618201726280.png
Normal file
|
After Width: | Height: | Size: 66 KiB |
BIN
自学/assets/image-20210618201912078.png
Normal file
|
After Width: | Height: | Size: 17 KiB |
BIN
自学/assets/image-20210618202047575.png
Normal file
|
After Width: | Height: | Size: 177 KiB |
BIN
自学/assets/image-20210618202322301.png
Normal file
|
After Width: | Height: | Size: 39 KiB |
BIN
自学/assets/image-20210618202334536.png
Normal file
|
After Width: | Height: | Size: 200 KiB |
BIN
自学/assets/image-20210618202433356.png
Normal file
|
After Width: | Height: | Size: 74 KiB |
BIN
自学/assets/image-20210618202449881.png
Normal file
|
After Width: | Height: | Size: 71 KiB |
BIN
自学/assets/image-20210618202501928.png
Normal file
|
After Width: | Height: | Size: 17 KiB |
BIN
自学/assets/image-20210618202701492.png
Normal file
|
After Width: | Height: | Size: 104 KiB |
BIN
自学/assets/image-20210715193149837.png
Normal file
|
After Width: | Height: | Size: 47 KiB |
BIN
自学/assets/image-20210715193224094.png
Normal file
|
After Width: | Height: | Size: 29 KiB |
BIN
自学/assets/image-20210715193334367.png
Normal file
|
After Width: | Height: | Size: 18 KiB |
BIN
自学/assets/image-20210715193414601.png
Normal file
|
After Width: | Height: | Size: 12 KiB |
BIN
自学/assets/image-20210715193730096.png
Normal file
|
After Width: | Height: | Size: 54 KiB |
BIN
自学/assets/image-20210715193838719.png
Normal file
|
After Width: | Height: | Size: 39 KiB |
BIN
自学/assets/image-20210715193914039.png
Normal file
|
After Width: | Height: | Size: 68 KiB |
BIN
自学/assets/image-20210715194137982.png
Normal file
|
After Width: | Height: | Size: 25 KiB |
BIN
自学/assets/image-20210715194413178.png
Normal file
|
After Width: | Height: | Size: 51 KiB |
BIN
自学/assets/image-20210715195053807.png
Normal file
|
After Width: | Height: | Size: 65 KiB |
BIN
自学/assets/image-20210715195144130.png
Normal file
|
After Width: | Height: | Size: 49 KiB |
BIN
自学/assets/image-20210715195410764.png
Normal file
|
After Width: | Height: | Size: 77 KiB |
BIN
自学/assets/image-20210715195844978.png
Normal file
|
After Width: | Height: | Size: 51 KiB |
BIN
自学/assets/image-20210715200155537.png
Normal file
|
After Width: | Height: | Size: 50 KiB |
BIN
自学/assets/image-20210715200243194.png
Normal file
|
After Width: | Height: | Size: 36 KiB |
BIN
自学/assets/image-20210715200336526.png
Normal file
|
After Width: | Height: | Size: 191 KiB |
516
自学/微服务.md
@ -1,5 +1,167 @@
|
||||
# 微服务
|
||||
|
||||
## 踩坑总结
|
||||
|
||||
### 包扫描问题(非常容易出错!)
|
||||
|
||||
以 Spring Boot 为例,框架默认会扫描启动类所在包及其子包中的组件(`@Component`/`@Service`/`@Repository`/`@Configuration` 等),将它们注册到 Spring 容器中。
|
||||
|
||||
**问题**:当你把某些业务组件、配置类或第三方模块放在了启动类的同级或平级包下(而非子包),却没有手动指定扫描路径,就会出现 “无法注入 Bean” 的情况。
|
||||
|
||||
```java
|
||||
// 启动类
|
||||
@SpringBootApplication
|
||||
public class OrderServiceApplication { … }
|
||||
|
||||
// 业务类位于 com.example.common 包
|
||||
@Service
|
||||
public class PaymentClient { … }
|
||||
|
||||
```
|
||||
|
||||
如果项目结构是:
|
||||
|
||||
```text
|
||||
com.example.orderservice ← 启动类
|
||||
com.example.common ← 依赖组件
|
||||
|
||||
```
|
||||
|
||||
默认情况下 `com.example.common` 不会被扫描到,导致注入 `PaymentClient` 时抛出 `NoSuchBeanDefinitionException`。
|
||||
|
||||
|
||||
|
||||
解决方案:
|
||||
|
||||
1)显式指定扫描路径**:
|
||||
|
||||
```java
|
||||
@SpringBootApplication
|
||||
@ComponentScan(basePackages = {
|
||||
"com.example.orderservice",
|
||||
"com.example.common"
|
||||
})
|
||||
public class OrderServiceApplication { … }
|
||||
|
||||
```
|
||||
|
||||
2)**使用 `@Import` 或者 Spring Cloud 的自动配置机制**(如编写 `spring.factories`,让依赖模块自动装配)。
|
||||
|
||||
|
||||
|
||||
### 数据库连接池
|
||||
|
||||
**为什么需要?**
|
||||
|
||||
每次通过 JDBC 调用 `DriverManager.getConnection(...)`,都要完成网络握手、权限验证、初始化会话等大量开销,通常耗时在几十到几百毫秒不等。连接池通过**提前建立好 N 条物理连接**并在应用各处循环复用,避免了反复的开销。
|
||||
|
||||
**流程**
|
||||
|
||||
数据库连接池在应用启动时**预先创建**一定数量的物理连接,并将它们保存在空闲队列中;当业务需要访问数据库时,直接**从池中“借用”一个连接**(无需新建),**用完后调用 `close()` 即把它归还**池中;池会根据空闲超时或最大寿命策略自动回收旧连接,并在借出或定期扫描时执行简单心跳(如 `SELECT 1`)来剔除失效连接,确保始终有可用、健康的连接供高并发场景下快速复用。
|
||||
|
||||
```scss
|
||||
┌─────────────────────────────────────────┐
|
||||
│ 应用线程 A 调用 getConnection() │
|
||||
│ ┌──────────┐ ┌─────────────┐ │
|
||||
│ │ 空闲连接队列 │──取出──▶│ 物理连接 │───┐│
|
||||
│ └──────────┘ └─────────────┘ ││
|
||||
│ (代理包装) ││
|
||||
│ 返回代理连接给业务代码 ││
|
||||
└─────────────────────────────────────────┘ │
|
||||
│
|
||||
┌─────────────────────────────────────────┐ │
|
||||
│ 业务执行 SQL,最后调用 close() │
|
||||
│ ┌───────────────┐ ┌────────────┐ │
|
||||
│ │ 代理 Connection │──归还──▶│ 空闲连接队列 │◀─────┘
|
||||
│ └───────────────┘ └────────────┘
|
||||
└─────────────────────────────────────────┘
|
||||
|
||||
```
|
||||
|
||||
当你从连接池里拿到一个底层已被远程关闭的连接时,HikariCP(以及大多数成熟连接池)会在“借出”前先做一次简易校验(默认为 `Connection.isValid()`,或你配置的 `connection-test-query`)。如果校验失败,连接池会自动将这条“死”连接销毁,**并尝试从池里或新建一个新的物理连接来替换**,再把新的健康连接返给业务;只有当新的连接也创建或校验失败到达池的最大重试次数时,才会抛出拿不到连接的超时异常。
|
||||
|
||||
|
||||
|
||||
**遇到的问题**
|
||||
|
||||
如果本地启动了 Java 应用和前端 Nginx,而 MySQL 部署在远程服务器上,Java 应用通过连接池与远程数据库建立的 TCP 连接在 5 分钟内若无任何 SQL 操作,就会因中间网络设备(如 NAT、负载均衡器、防火墙)超时断开,且应用层不会主动感知,导致后续 SQL 请求失败。
|
||||
|
||||
```shell
|
||||
13:20:01:383 WARN 43640 --- [nio-8084-exec-4] com.zaxxer.hikari.pool.PoolBase : HikariPool-1 - Failed to validate connection com.mysql.cj.jdbc.ConnectionImpl@36e971ae (No operations allowed after connection closed.). Possibly consider using a shorter maxLifetime value.
|
||||
13:20:01:384 ERROR 43640 --- [nio-8084-exec-4] o.a.c.c.C.[.[.[/].[dispatcherServlet] : Servlet.service() for servlet [dispatcherServlet] in context with path [] threw exception [Request processing failed; nested exception is org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.exceptions.PersistenceException:
|
||||
### Error querying database. Cause: org.springframework.jdbc.CannotGetJdbcConnectionException: Failed to obtain JDBC Connection; nested exception is java.sql.SQLTransientConnectionException: HikariPool-1 - Connection is not available, request timed out after 30048ms.
|
||||
```
|
||||
|
||||
为了解决这个问题,
|
||||
|
||||
1.只需在 Spring Boot 配置中为 HikariCP 添加定期心跳,让连接池在真正断连前保持流量:
|
||||
|
||||
```
|
||||
spring:
|
||||
datasource:
|
||||
hikari:
|
||||
keepalive-time: 180000 # 3 分钟发送一次心跳(维持 TCP 活跃)
|
||||
```
|
||||
|
||||
这样,HikariCP 会每隔 3 分钟自动对空闲连接执行轻量级的验证操作(如 `Connection.isValid()`),确保中间网络链路不会因长时间静默而被强制关闭。
|
||||
|
||||
|
||||
|
||||
2.如果JAVA应用和Mysql在同一服务器上(可互通),就不会有上述问题!
|
||||
|
||||
|
||||
|
||||
### Sentinel无数据
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/25/uaviaj-0.png" alt="image-20250525183228831" style="zoom:67%;" />
|
||||
|
||||
sentinel 控制台可以发现哪些微服务连接了,但是Dashboard 在尝试去拿各个微服务上报的规则(端点 `/getRules`)和指标(端点 `/metric`)时,一直连不上它们,因为JAVA微服务是在本地私网内部署的,Dashboard无法连接上。
|
||||
|
||||
```shell
|
||||
Failed to fetch metric from http://192.168.0.107:8725/metric?…
|
||||
Failed to fetch metric from http://192.168.0.107:8721/metric?…
|
||||
HTTP request failed: http://192.168.0.107:8721/getRules?type=flow
|
||||
java.net.ConnectException: Operation timed out
|
||||
```
|
||||
|
||||
解决办法:
|
||||
|
||||
1.将JAVA应用部署到服务器,但我的服务器内存不够
|
||||
|
||||
2.将Dashboard部署到本机docker中,和JAVA应用可互通。
|
||||
|
||||
|
||||
|
||||
### Nacos迁移后的 No DataSource set
|
||||
|
||||
原本Nacos和Mysql都是部署到公网服务器,mysql容器对外暴露3307,因此Nacos的env文件中可以是:
|
||||
|
||||
```env
|
||||
MYSQL_SERVICE_DB_NAME=124.xxx.xxx.xxx
|
||||
MYSQL_SERVICE_PORT=3307
|
||||
```
|
||||
|
||||
填的mysql的公网ip,以及它暴露的端口3307,这是OK的
|
||||
|
||||
|
||||
|
||||
**但是**如果将它们部署在docker同一网络中,应该这样写:
|
||||
|
||||
```
|
||||
MYSQL_SERVICE_DB_NAME=mysql
|
||||
MYSQL_SERVICE_PORT=3306
|
||||
```
|
||||
|
||||
mysql是服务名,不能写localhost(或 `127.0.0.1`),它永远只会指向「当前容器自己」!!!
|
||||
|
||||
|
||||
|
||||
注意,Nacos中的配置文件**也要迁移过来**,导入nacos配置列表中,并且修改JAVA项目中nacos的地址
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/24/s9s6am-0.png" alt="image-20250524170952380" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
## 认识微服务
|
||||
|
||||
微服务架构,首先是服务化,就是将单体架构中的功能模块从单体应用中拆分出来,独立部署为多个服务。
|
||||
@ -335,7 +497,6 @@ package com.hmall.cart;
|
||||
@SpringBootApplication
|
||||
public class CartApplication {
|
||||
public static void main(String[] args) {
|
||||
|
||||
SpringApplication.run(CartApplication.class, args);
|
||||
}
|
||||
}
|
||||
@ -437,6 +598,8 @@ spring:
|
||||
| Before | 是某个时间点之前的请求 | - Before=2031-04-13T15:14:47.433+08:00[Asia/Shanghai] |
|
||||
| Path | 请求路径必须符合指定规则 | - Path=/red/{segment},/blue/** |
|
||||
|
||||
如果(predicates)符合这些规则,就把请求送到(uri)这里去。
|
||||
|
||||
|
||||
|
||||
**Ant风格路径**
|
||||
@ -707,8 +870,25 @@ public class DefaultFeignConfig {
|
||||
basePackages = "com.hmall.api.client",
|
||||
defaultConfiguration = DefaultFeignConfig.class
|
||||
)
|
||||
@SpringBootApplication
|
||||
public class PayApplication {
|
||||
```
|
||||
|
||||
这样 `DefaultFeignConfig.class` 会对于所有Client类生效
|
||||
|
||||
|
||||
|
||||
```java
|
||||
@FeignClient(value = "item-service",
|
||||
configuration = DefaultFeignConfig.class)
|
||||
public interface ItemClient {
|
||||
@GetMapping("/items")
|
||||
List<ItemDTO> queryItemByIds(@RequestParam("ids") Collection<Long> ids);
|
||||
}
|
||||
```
|
||||
|
||||
这种只对ItemClient生效!
|
||||
|
||||
|
||||
|
||||
**整体流程图**
|
||||
@ -793,7 +973,7 @@ hm:
|
||||
|
||||
### 配置热更新
|
||||
|
||||
有很多的业务相关参数,将来可能会根据实际情况临时调整,如何不重启服务,直接更改配置文件生效呢?
|
||||
有很多的业务相关参数,将来可能会根据实际情况临时调整,如何**不重启服务**,直接更改配置文件生效呢?
|
||||
|
||||
示例:购物车中的商品上限数量需动态调整。
|
||||
|
||||
@ -821,8 +1001,6 @@ hm:
|
||||
maxAmount: 1 # 购物车商品数量上限
|
||||
```
|
||||
|
||||
|
||||
|
||||
2)在微服务中配置
|
||||
|
||||
```java
|
||||
@ -834,6 +1012,334 @@ public class CartProperties {
|
||||
}
|
||||
```
|
||||
|
||||
3)下次,只需改nacos中的配置文件=》发布,即可实现热更新。
|
||||
|
||||
|
||||
下次,只需改nacos中的配置,即可实现热更新。
|
||||
|
||||
### 动态路由
|
||||
|
||||
**1.监听Nacos的配置变更**
|
||||
|
||||
`NacosConfigManager`可以获取`ConfigService `配置信息
|
||||
|
||||
`String configInfo = nacosConfigManager.getConfigService()`
|
||||
|
||||
内容是带换行和缩进的 YAML 文本或者 **JSON 格式**(取决于你的配置文件格式):
|
||||
|
||||
```json
|
||||
//多条路由
|
||||
[
|
||||
{
|
||||
"id": "user-service",
|
||||
"uri": "lb://USER-SERVICE",
|
||||
"predicates": [
|
||||
"Path=/user/**"
|
||||
],
|
||||
"filters": [
|
||||
"StripPrefix=1"
|
||||
]
|
||||
},
|
||||
{
|
||||
"id": "order-service",
|
||||
"uri": "lb://ORDER-SERVICE",
|
||||
"predicates": [
|
||||
"Path=/order/**"
|
||||
],
|
||||
"filters": [
|
||||
"StripPrefix=1",
|
||||
"AddRequestHeader=X-Order-Source,cloud"
|
||||
]
|
||||
}
|
||||
]
|
||||
```
|
||||
|
||||
因为YAML格式解析不方便,故配置文件采用 JSON 格式保存、读取、解析!
|
||||
|
||||
|
||||
|
||||
```Java
|
||||
String getConfigAndSignListener(
|
||||
String dataId, // 配置文件id
|
||||
String group, // 配置组,走默认
|
||||
long timeoutMs, // 读取配置的超时时间
|
||||
Listener listener // 监听器
|
||||
) throws NacosException;
|
||||
```
|
||||
|
||||
`getConfigAndSignListener`既可以在第一次**读配置**文件又可以在后面进行**监听**
|
||||
|
||||
每当 Nacos 上该配置有变更,会触发其内部`receiveConfigInfo(...)` 方法
|
||||
|
||||
|
||||
|
||||
**2.然后手动把最新的路由更新到路由表中。**
|
||||
|
||||
`RouteDefinitionWriter`
|
||||
|
||||
```java
|
||||
public interface RouteDefinitionWriter {
|
||||
/**
|
||||
* 更新路由到路由表,如果路由id重复,则会覆盖旧的路由
|
||||
*/
|
||||
Mono<Void> save(Mono<RouteDefinition> route);
|
||||
/**
|
||||
* 根据路由id删除某个路由
|
||||
*/
|
||||
Mono<Void> delete(Mono<String> routeId);
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
```java
|
||||
@Slf4j
|
||||
@Component
|
||||
@RequiredArgsConstructor
|
||||
public class DynamicRouteLoader {
|
||||
|
||||
private final RouteDefinitionWriter writer;
|
||||
private final NacosConfigManager nacosConfigManager;
|
||||
|
||||
// 路由配置文件的id和分组
|
||||
private final String dataId = "gateway-routes.json";
|
||||
private final String group = "DEFAULT_GROUP";
|
||||
// 保存更新过的路由id
|
||||
private final Set<String> routeIds = new HashSet<>(); //order-service ...
|
||||
|
||||
@PostConstruct
|
||||
public void initRouteConfigListener() throws NacosException {
|
||||
// 1.注册监听器并首次拉取配置
|
||||
String configInfo = nacosConfigManager.getConfigService()
|
||||
.getConfigAndSignListener(dataId, group, 5000, new Listener() {
|
||||
@Override
|
||||
public Executor getExecutor() {
|
||||
return null;
|
||||
}
|
||||
|
||||
@Override
|
||||
public void receiveConfigInfo(String configInfo) {
|
||||
updateConfigInfo(configInfo);
|
||||
}
|
||||
});
|
||||
// 2.首次启动时,更新一次配置
|
||||
updateConfigInfo(configInfo);
|
||||
}
|
||||
|
||||
private void updateConfigInfo(String configInfo) {
|
||||
log.debug("监听到路由配置变更,{}", configInfo);
|
||||
// 1.反序列化
|
||||
List<RouteDefinition> routeDefinitions = JSONUtil.toList(configInfo, RouteDefinition.class);
|
||||
// 2.更新前先清空旧路由
|
||||
// 2.1.清除旧路由
|
||||
for (String routeId : routeIds) {
|
||||
writer.delete(Mono.just(routeId)).subscribe();
|
||||
}
|
||||
routeIds.clear();
|
||||
// 2.2.判断是否有新的路由要更新
|
||||
if (CollUtils.isEmpty(routeDefinitions)) {
|
||||
// 无新路由配置,直接结束
|
||||
return;
|
||||
}
|
||||
// 3.更新路由
|
||||
routeDefinitions.forEach(routeDefinition -> {
|
||||
// 3.1.更新路由
|
||||
writer.save(Mono.just(routeDefinition)).subscribe();
|
||||
// 3.2.记录路由id,方便将来删除
|
||||
routeIds.add(routeDefinition.getId());
|
||||
});
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可以在项目启动时先更新一次路由,后续随着配置变更通知到监听器,完成路由更新。
|
||||
|
||||
|
||||
|
||||
## 服务保护与分布式事务
|
||||
|
||||
### 服务保护方案
|
||||
|
||||
**1)请求限流**
|
||||
|
||||
**限制或控制**接口访问的并发流量,避免服务因流量激增而出现故障。
|
||||
|
||||
**2)线程隔离**
|
||||
|
||||
为了避免某个接口故障或压力过大导致整个服务不可用,我们可以限定每个接口可以使用的资源范围,也就是将其“隔离”起来。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/25/pnn2tm-0.png" alt="image-20250525155132474" style="zoom: 80%;" />
|
||||
|
||||
**3)服务熔断**
|
||||
|
||||
线程隔离虽然避免了雪崩问题,但故障服务(商品服务)依然会拖慢购物车服务(服务调用方)的接口响应速度。
|
||||
|
||||
所以,我们要做两件事情:
|
||||
|
||||
- **编写服务降级逻辑**:就是服务调用失败后的处理逻辑,根据业务场景,可以抛出异常,也可以返回友好提示或**默认数据**。
|
||||
- **异常统计和熔断**:统计服务提供方的异常比例,当比例过高表明该接口会影响到其它服务,应该拒绝调用该接口,而是直接走降级逻辑。
|
||||
|
||||
无非就是停止无意义的等待,直接返回Fallback方案。
|
||||
|
||||
|
||||
|
||||
### Sentinel
|
||||
|
||||
#### 介绍和安装
|
||||
|
||||
Sentinel是阿里巴巴开源的一款服务保护框架,[quick-start | Sentinel](https://sentinelguard.io/zh-cn/docs/quick-start.html)
|
||||
|
||||
| 特性 | Sentinel (阿里巴巴) | Hystrix (网飞) |
|
||||
| -------- | ---------------------------------------------- | ---------------------------- |
|
||||
| 线程隔离 | 信号量隔离 | 线程池隔离 / 信号量隔离 |
|
||||
| 熔断策略 | 基于慢调用比例或异常比例 | 基于异常比率 |
|
||||
| 限流 | 基于 QPS,支持流量整形 | 有限的支持 |
|
||||
| Fallback | 支持 | 支持 |
|
||||
| 控制台 | 开箱即用,可配置规则、查看秒级监控、机器发现等 | 不完善 |
|
||||
| 配置方式 | 基于控制台,重启后失效 | 基于注解或配置文件,永久生效 |
|
||||
|
||||
**安装:**
|
||||
|
||||
1)下载jar包 https://github.com/alibaba/Sentinel/releases
|
||||
|
||||
2)将jar包放在任意非中文、不包含特殊字符的目录下,重命名为`sentinel-dashboard.jar`
|
||||
|
||||
然后运行如下命令启动控制台:
|
||||
|
||||
```Shell
|
||||
java -Dserver.port=8090 -Dcsp.sentinel.dashboard.server=localhost:8090 -Dproject.name=sentinel-dashboard -jar sentinel-dashboard.jar
|
||||
```
|
||||
|
||||
3)访问[http://localhost:8090](http://localhost:8080)页面,就可以看到sentinel的控制台了
|
||||
|
||||
账号和密码,默认都是:sentinel
|
||||
|
||||
**微服务整合**
|
||||
|
||||
1)引入依赖
|
||||
|
||||
```xml
|
||||
<!--sentinel-->
|
||||
<dependency>
|
||||
<groupId>com.alibaba.cloud</groupId>
|
||||
<artifactId>spring-cloud-starter-alibaba-sentinel</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2)配置控制台
|
||||
|
||||
修改application.yaml文件(可以用共享配置nacos),添加如下:
|
||||
|
||||
```yml
|
||||
spring:
|
||||
cloud:
|
||||
sentinel:
|
||||
transport:
|
||||
dashboard: localhost:8090
|
||||
```
|
||||
|
||||
|
||||
|
||||
我们的SpringMVC接口是按照Restful风格设计,因此购物车的查询、删除、修改等接口全部都是`/carts`路径。默认情况下Sentinel会把路径作为簇点资源的名称,无法区分路径相同但**请求方式不同**的接口。
|
||||
|
||||
可以在`application.yml`中添加下面的配置 然后,**重启**服务
|
||||
|
||||
```yaml
|
||||
spring:
|
||||
cloud:
|
||||
sentinel:
|
||||
transport:
|
||||
dashboard: localhost:8090
|
||||
http-method-specify: true # 开启请求方式前缀
|
||||
```
|
||||
|
||||
|
||||
|
||||
**OpenFeign整合Sentinel**
|
||||
|
||||
默认sentinel只会整合spring mvc中的接口。
|
||||
|
||||
修改cart-service模块的application.yml文件,可开启Feign的sentinel功能:
|
||||
|
||||
```yaml
|
||||
feign:
|
||||
sentinel:
|
||||
enabled: true # 开启feign对sentinel的支持
|
||||
```
|
||||
|
||||
调用的别的服务(/item-service)的接口也会显示在这。
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
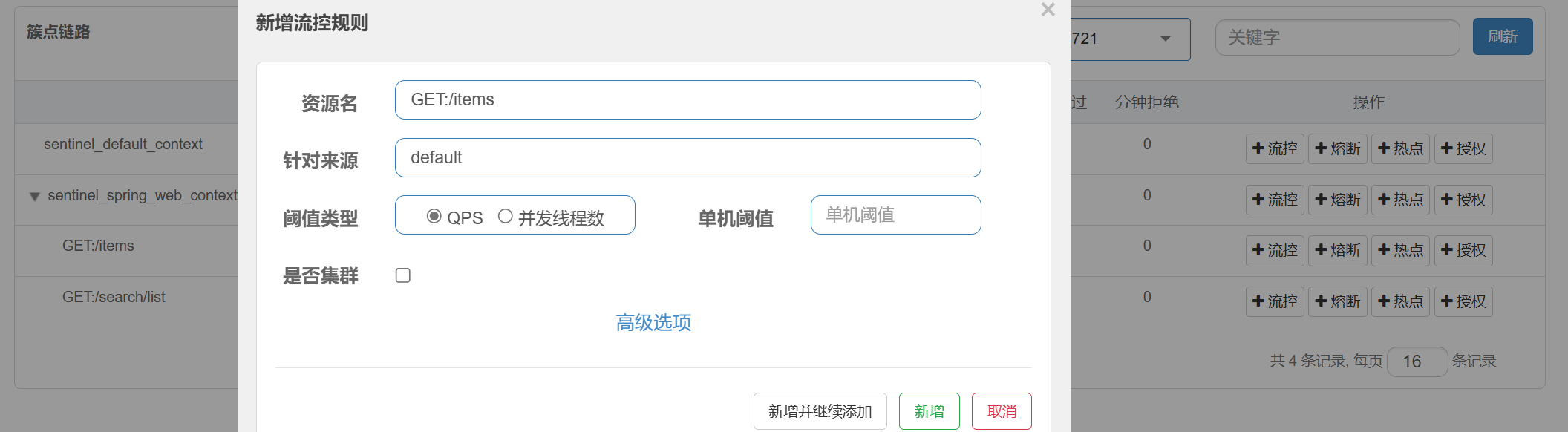
#### 限流:
|
||||
|
||||
|
||||
|
||||
直接在sentinel控制台->簇点链路->流控 里面设置QPS
|
||||
|
||||
|
||||
|
||||
#### 线程隔离
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/26/umzjz1-0.png" alt="image-20250526185301904" style="zoom: 67%;" />
|
||||
|
||||
阈值类型选 **并发线程数** ,代表这个接口所能用的线程数。
|
||||
|
||||
|
||||
|
||||
#### Fallback
|
||||
|
||||
触发限流或熔断后的请求不一定要直接报错,也可以返回一些默认数据或者友好提示,采用FallbackFactory,可以对远程调用的异常做处理。
|
||||
|
||||
**步骤一**:在hm-api模块中给`ItemClient`定义降级处理类,实现`FallbackFactory`:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/05/26/x2wpbf-0.png" alt="image-20250526200028905" style="zoom:80%;" />
|
||||
|
||||
```
|
||||
public class ItemClientFallback implements FallbackFactory<ItemClient> {
|
||||
@Override
|
||||
public ItemClient create(Throwable cause) {
|
||||
return new ItemClient() {
|
||||
@Override
|
||||
public List<ItemDTO> queryItemByIds(Collection<Long> ids) {
|
||||
log.error("远程调用ItemClient#queryItemByIds方法出现异常,参数:{}", ids, cause);
|
||||
// 查询购物车允许失败,查询失败,返回空集合
|
||||
return CollUtils.emptyList();
|
||||
}
|
||||
|
||||
@Override
|
||||
public void deductStock(List<OrderDetailDTO> items) {
|
||||
// 库存扣减业务需要触发事务回滚,查询失败,抛出异常
|
||||
throw new BizIllegalException(cause);
|
||||
}
|
||||
};
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**步骤二**:在`hm-api`模块中的`com.hmall.api.config.DefaultFeignConfig`类中将`ItemClientFallback`注册为一个`Bean`:
|
||||
|
||||
```java
|
||||
@Bean
|
||||
public ItemClientFallback itemClientFallback(){
|
||||
return new ItemClientFallback();
|
||||
}
|
||||
```
|
||||
|
||||
**步骤三**:在`hm-api`模块中的`ItemClient`接口中使用`ItemClientFallbackFactory`:
|
||||
|
||||
```java
|
||||
@FeignClient(value = "item-service",fallbackFactory = ItemClientFallback.class)
|
||||
public interface ItemClient {
|
||||
@GetMapping("/items")
|
||||
List<ItemDTO> queryItemByIds(@RequestParam("ids") Collection<Long> ids);
|
||||
}
|
||||
```
|
||||
|
||||
重启后,再次测试
|
||||
|
||||
@ -1,9 +1,5 @@
|
||||
# 苍穹外卖
|
||||
|
||||
## 踩坑总结
|
||||
|
||||
|
||||
|
||||
## 项目简介
|
||||
|
||||
### 整体介绍
|
||||
|
||||