Commit on 2025/07/03 周四 17:41:09.50
This commit is contained in:
parent
426ef21fe2
commit
2c71156c3c
110
科研/ZY网络重构分析.md
110
科研/ZY网络重构分析.md
@ -388,34 +388,128 @@ $$
|
|||||||
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^r \Delta \lambda_m ({x}_m {x}_m^T)_{ij} \right| < \frac{1}{2}
|
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^r \Delta \lambda_m ({x}_m {x}_m^T)_{ij} \right| < \frac{1}{2}
|
||||||
$$
|
$$
|
||||||
|
|
||||||
于一个归一化的特征向量 ${x}_m$,其外积矩阵$ {x}_m {x}_m^T$ 满足
|
于一个归一化的特征向量 ${x}_m$,非对角线上元素,其外积矩阵$ {x}_m {x}_m^T$ 满足
|
||||||
$$
|
$$
|
||||||
|({x}_m {x}_m^T)_{ij}| \leq 1.
|
|({x}_m {x}_m^T)_{ij}| \leq \frac12.
|
||||||
$$
|
$$
|
||||||
例:
|
例:
|
||||||
$$
|
$$
|
||||||
x_m = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\\
|
x_m = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\\
|
||||||
x_m x_m^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
x_m x_m^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
||||||
$$
|
$$
|
||||||
每个元素的绝对值$\leq1$
|
每个元素的绝对值$\frac12$
|
||||||
|
|
||||||
|
|
||||||
$$
|
$$
|
||||||
\left| \sum_{m=1}^r \Delta \lambda_m (x_m x_m^T)_{ij} \right| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m|.
|
\left| \sum_{m=1}^r \Delta \lambda_m (x_m x_m^T)_{ij} \right| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| \leq \frac12\sum_{m=1}^r |\Delta \lambda_m|.
|
||||||
$$
|
$$
|
||||||
为了确保 $|a_{ij} - \widetilde{a}_{ij}| < \frac{1}{2}$ 对所有 $(i,j)$ 成立,网络精准重构条件为:
|
为了确保 $|a_{ij} - \widetilde{a}_{ij}| < \frac{1}{2}$ 对所有 $(i,j)$ 成立,网络精准重构条件为:
|
||||||
$$
|
$$
|
||||||
\sum_{m=1}^r\left| \Delta \lambda_m\right| < \frac{1}{2}
|
\sum_{m=1}^r\left| \Delta \lambda_m\right| < 1
|
||||||
$$
|
$$
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
### 考虑特征向量的扰动:
|
||||||
|
|
||||||
|
**1 将差分拆成"特征值项 + 特征向量项"**
|
||||||
|
|
||||||
|
对称矩阵 $A,\;\tilde A$ 的前 $r$ 个特征对分别记作
|
||||||
|
$\{(\lambda_m,x_m)\}_{m=1}^r,\; \{(\tilde\lambda_m,\tilde x_m)\}_{m=1}^r$。
|
||||||
|
$$
|
||||||
|
\begin{aligned}
|
||||||
|
A-\tilde A
|
||||||
|
&=\sum_{m=1}^r\bigl(\lambda_m x_mx_m^\top-\tilde\lambda_m\tilde x_m\tilde x_m^\top\bigr)\\
|
||||||
|
&=\underbrace{\sum_{m=1}^r\Delta\lambda_m\,x_mx_m^\top}_{\text{特征值扰动}}
|
||||||
|
\;+\;
|
||||||
|
\underbrace{\sum_{m=1}^r
|
||||||
|
\tilde\lambda_m\bigl(x_mx_m^\top-\tilde x_m\tilde x_m^\top\bigr)}_{\text{特征向量扰动}} .
|
||||||
|
\end{aligned}
|
||||||
|
$$
|
||||||
|
|
||||||
|
---
|
||||||
|
|
||||||
|
**2 如何控制"特征向量扰动项"**
|
||||||
|
|
||||||
|
设 $\theta_m:=\angle(x_m,\tilde x_m)$,
|
||||||
|
则 rank-1 投影差满足
|
||||||
|
$$
|
||||||
|
\|x_mx_m^\top-\tilde x_m\tilde x_m^\top\|_2=\sin\theta_m,
|
||||||
|
$$
|
||||||
|
而单个元素绝对值永远不超过谱范数,
|
||||||
|
所以
|
||||||
|
$$
|
||||||
|
\bigl| (x_mx_m^\top-\tilde x_m\tilde x_m^\top)_{ij}\bigr|
|
||||||
|
\;\le\;\sin\theta_m .
|
||||||
|
$$
|
||||||
|
|
||||||
|
要把 $\sin\theta_m$ 换成 **只含特征值的量**,用 Davis-Kahan *sin θ* 定理。
|
||||||
|
设
|
||||||
|
$$
|
||||||
|
\gamma_m:=\min_{k\neq m}\lvert\lambda_m-\lambda_k\rvert
|
||||||
|
\quad(\text{与其它特征值的最小间隔}),
|
||||||
|
$$
|
||||||
|
当$\|\tilde A-A\|_2$ 足够小(或直接用 Weyl 定理把它替换成 $|\Delta\lambda_m|$)时
|
||||||
|
|
||||||
|
$$
|
||||||
|
\sin\theta_m
|
||||||
|
\;\le\;
|
||||||
|
\frac{\lvert\Delta\lambda_m\rvert}{\gamma_m}
|
||||||
|
\quad\text{(单向版本的 Davis-Kahan)}\;
|
||||||
|
$$
|
||||||
|
|
||||||
|
**3 元素级误差的统一上界**
|
||||||
|
|
||||||
|
把两部分误差放在一起,对 **非对角元** ($|x_{mi}x_{mj}|\le\tfrac12$ 的情形) 有
|
||||||
|
|
||||||
|
$$
|
||||||
|
\begin{aligned}
|
||||||
|
\lvert a_{ij}-\tilde a_{ij}\rvert
|
||||||
|
&\le
|
||||||
|
\frac12\sum_{m=1}^r\lvert\Delta\lambda_m\rvert
|
||||||
|
\;+\;
|
||||||
|
\sum_{m=1}^r
|
||||||
|
\lvert\tilde\lambda_m\rvert\,
|
||||||
|
\sin\theta_m\\[4pt]
|
||||||
|
&\le
|
||||||
|
\frac12\sum_{m=1}^r\lvert\Delta\lambda_m\rvert
|
||||||
|
\;+\;
|
||||||
|
\sum_{m=1}^r
|
||||||
|
\lvert\tilde\lambda_m\rvert\,
|
||||||
|
\frac{\lvert\Delta\lambda_m\rvert}{\gamma_m}.
|
||||||
|
\end{aligned}
|
||||||
|
$$
|
||||||
|
|
||||||
|
---
|
||||||
|
|
||||||
|
**4 纯"特征值—谱隙"条件**
|
||||||
|
|
||||||
|
若要保证 **所有** 非对角元素都 < $\tfrac12$,只需让
|
||||||
|
|
||||||
|
$$
|
||||||
|
\boxed{\;
|
||||||
|
\sum_{m=1}^r
|
||||||
|
\lvert\Delta\lambda_m\rvert
|
||||||
|
\Bigl(
|
||||||
|
\tfrac12+\frac{\lvert\tilde\lambda_m\rvert}{\gamma_m}
|
||||||
|
\Bigr)
|
||||||
|
\;<\;
|
||||||
|
\tfrac12
|
||||||
|
\;}
|
||||||
|
\tag{★}
|
||||||
|
$$
|
||||||
|
|
||||||
|
这就是你原先
|
||||||
|
$\displaystyle\sum_{m=1}^r\lvert\Delta\lambda_m\rvert<1$
|
||||||
|
的推广版本:
|
||||||
|
|
||||||
|
* 若谱隙 $\gamma_m$ **很大**,第二项趋于 0,(★) 近似退化到你的条件;
|
||||||
|
* 当 $\gamma_m$ 变小(特征值接近重数高或"纠缠"),就必须更严格地控制 $\Delta\lambda_m$。
|
||||||
|
|
||||||
|
对角元素的最坏情况 $|x_{mi}|^2=1$ 时,只要把公式里的前系数 ½ 改成 1 即可。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如果在**高层次**(特征值滤波)的误差累积超过了一定阈值,就有可能在**低层次**(邻接矩阵元素)中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5,就可以保证0-1矩阵的精确重构。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## **非0/1矩阵**
|
## **非0/1矩阵**
|
||||||
|
|||||||
@ -286,7 +286,7 @@ $$
|
|||||||
|
|
||||||
# 无迹卡尔曼(UKF)
|
# 无迹卡尔曼(UKF)
|
||||||
|
|
||||||
#### UKF 具体步骤(分步解析)
|
### UKF 具体步骤(分步解析)
|
||||||
|
|
||||||
| 符号 | 含义 | 维度 |
|
| 符号 | 含义 | 维度 |
|
||||||
| ------------------------- | ------------------------------ | ------------------- |
|
| ------------------------- | ------------------------------ | ------------------- |
|
||||||
|
|||||||
153
科研/草稿.md
153
科研/草稿.md
@ -1,118 +1,57 @@
|
|||||||
根据您提供的图片内容和数学符号描述,当前的公式和符号使用**基本符合数学和论文规范**,但可以进一步优化以提高严谨性和可读性。以下是具体分析及建议:
|
Here's the reformatted version with Markdown + LaTeX, including explanations for the `*` symbol:
|
||||||
|
|
||||||
------
|
---
|
||||||
|
|
||||||
### **1. 邻接矩阵 `A` 的表示**
|
**Input**:
|
||||||
|
- Ordered singular value estimates
|
||||||
|
$$\tilde\sigma_1 \ge \tilde\sigma_2 \ge \cdots \ge \tilde\sigma_r,$$
|
||||||
|
- Budget
|
||||||
|
$$s \ge 0.$$
|
||||||
|
|
||||||
- **当前表述**:
|
---
|
||||||
`A = a_{ij} \ (i,j \in 1,2,\ldots,n)`
|
|
||||||
**合理性**:
|
|
||||||
- 矩阵元素 `a_{ij}` 的下标范围明确(`i,j` 从 1 到 `n`)。
|
|
||||||
- 声明 `A` 为实对称矩阵(`a_{ij} = a_{ji}`)符合图的邻接矩阵定义。
|
|
||||||
- **优化建议**:
|
|
||||||
- 若论文涉及离散时间或动态网络,建议将时间下标 `t` 包含在括号内,即 **`A_t = (a_{ij})_t`**,以强调时间依赖性(例如:`A_t` 是 `t` 时刻的邻接矩阵)。
|
|
||||||
- 如果时间 `t` 是次要因素,直接使用 `A` 或 `A(t)` 也可接受。
|
|
||||||
|
|
||||||
------
|
### 1. Prefix Sum Array Initialization
|
||||||
|
$$S = [0] * (r+1)$$
|
||||||
|
|
||||||
### **2. 矩阵元素的定义式**
|
> **Note**: The `*` symbol here is Python's list repetition operator, used to create a length $(r+1)$ array filled with zeros. In formal papers, this would typically be written as:
|
||||||
|
> $$S_0 = S_1 = \cdots = S_r = 0$$
|
||||||
|
> or more concisely:
|
||||||
|
> $$S = \mathbf{0}_{r+1}.$$
|
||||||
|
|
||||||
- **当前表述**:
|
### 2. Absolute Value Prefix Sum Computation
|
||||||
|
For $\kappa=1,2,\dots,r$:
|
||||||
|
$$
|
||||||
|
S[\kappa] = S[\kappa-1] + \bigl|\tilde\sigma_\kappa\bigr|.
|
||||||
|
$$
|
||||||
|
|
||||||
```
|
### 3. Search Threshold Calculation
|
||||||
a_{ij} = a_{ji} =
|
$$
|
||||||
\begin{cases}
|
\theta = S[r] - s.
|
||||||
w_{ij}, & d_{ij} \leq r \\
|
$$
|
||||||
0, & d_{ij} > r \text{ or } i = j
|
|
||||||
\end{cases}
|
|
||||||
```
|
|
||||||
|
|
||||||
**合理性**:
|
### 4. Binary Search on $S[0\ldots r]$
|
||||||
|
Find the minimal $\kappa$ satisfying:
|
||||||
|
$$
|
||||||
|
S[\kappa] \ge \theta.
|
||||||
|
$$
|
||||||
|
|
||||||
- 分段函数形式清晰,逻辑完整(覆盖了通信半径 `r`、距离 `d_{ij}`、自环 `i=j` 的情况)。
|
**Pseudocode** (Python-style):
|
||||||
- 权值 `w_{ij}` 的说明(如流量、带宽)符合实际应用场景。
|
```python
|
||||||
|
low, high = 0, r
|
||||||
|
while low < high:
|
||||||
|
mid = (low + high) // 2
|
||||||
|
if S[mid] < θ:
|
||||||
|
low = mid + 1
|
||||||
|
else:
|
||||||
|
high = mid
|
||||||
|
κ = low
|
||||||
|
```
|
||||||
|
|
||||||
- **优化建议**:
|
---
|
||||||
|
|
||||||
- **符号一致性**:若 `w_{ij}` 是时变的,建议改为 `w_{ij}(t)`,与 `A_t` 保持一致。
|
Key modifications:
|
||||||
- **自环明确性**:可补充说明“对角线元素 `a_{ii} = 0`”以避免歧义(部分文献允许自环权值非零)。
|
1. Replaced all occurrences of $\tilde\lambda$ with $\tilde\sigma$ for consistency with SVD notation
|
||||||
|
2. Maintained proper LaTeX formatting with `$$` for display equations
|
||||||
------
|
3. Added clear section headers
|
||||||
|
4. Preserved the Python-style pseudocode block
|
||||||
### **3. 时间下标的处理**
|
5. Included explanatory note about the `*` operator usage
|
||||||
|
|
||||||
-
|
|
||||||
|
|
||||||
用户疑问
|
|
||||||
|
|
||||||
:是否将
|
|
||||||
|
|
||||||
```
|
|
||||||
t
|
|
||||||
```
|
|
||||||
|
|
||||||
放在括号内(如
|
|
||||||
|
|
||||||
```
|
|
||||||
\lambda_i(A_t)
|
|
||||||
```
|
|
||||||
|
|
||||||
vs
|
|
||||||
|
|
||||||
```
|
|
||||||
\lambda_i(A)_t
|
|
||||||
```
|
|
||||||
|
|
||||||
)。
|
|
||||||
|
|
||||||
-
|
|
||||||
|
|
||||||
推荐写法
|
|
||||||
|
|
||||||
:
|
|
||||||
|
|
||||||
- 特征值/奇异值:统一用 **`\lambda_i(A_t)`** 或 **`\sigma_i(A_t)`**,表示“矩阵 `A_t` 的第 `i` 个特征值/奇异值”。
|
|
||||||
- 避免 `\lambda_i(A)_t`,因其可能被误解为“对 `A` 求特征值后再取时间 `t` 的分量”。
|
|
||||||
|
|
||||||
------
|
|
||||||
|
|
||||||
### **4. 其他细节规范**
|
|
||||||
|
|
||||||
-
|
|
||||||
|
|
||||||
符号字体
|
|
||||||
|
|
||||||
:
|
|
||||||
|
|
||||||
- 矩阵 `A` 用大写斜体,向量 `\mathbf{v}` 用小写粗体,标量 `r, d_{ij}` 用普通斜体。
|
|
||||||
- 确保希腊字母(如 `\lambda, \sigma`)和下标(如 `\text{max}, \text{min}`)的格式正确。
|
|
||||||
|
|
||||||
-
|
|
||||||
|
|
||||||
文字说明
|
|
||||||
|
|
||||||
:
|
|
||||||
|
|
||||||
- 对通信半径 `r`、距离 `d_{ij}`、权值 `w_{ij}` 的定义清晰,符合论文要求。
|
|
||||||
|
|
||||||
------
|
|
||||||
|
|
||||||
### **5. 总结建议**
|
|
||||||
|
|
||||||
- **动态网络场景**:
|
|
||||||
|
|
||||||
- 使用 `A_t` 和 `\lambda_i(A_t)`,保持时间下标在括号内。
|
|
||||||
|
|
||||||
- 示例修改:
|
|
||||||
|
|
||||||
> “动态网络的邻接矩阵序列 `\{A_t\}` 的特征值为 `\{\lambda_1(A_t), \ldots, \lambda_n(A_t)\}`。”
|
|
||||||
|
|
||||||
- **静态网络场景**:
|
|
||||||
|
|
||||||
- 直接使用 `A` 和 `\lambda_i(A)`,无需时间下标。
|
|
||||||
|
|
||||||
当前符号系统已足够规范,只需根据时间维度是否关键选择 **`A_t` 或 `A`**,并统一后续符号即可。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
$w_{ij}>0$
|
|
||||||
|
|||||||
26
科研/郭款论文.md
26
科研/郭款论文.md
@ -567,6 +567,16 @@ $$
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
**为什么采用SNMF?**
|
||||||
|
|
||||||
|
1.得到可解释、非负的低维表示 $U$,可以作为网络嵌入特征进行下游任务。
|
||||||
|
|
||||||
|
2.若直接特征分解,得到的B通常含有负值,导致 $A'$ 中元素可能存在负值。
|
||||||
|
|
||||||
|
3.$A' = U U^T$ ,由于 $U$ 是实对称矩阵,该算法得到的$A'$是正半定的,特征值都大于等于0。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**例:假设我们有一个 $3 \times 3$ 对称非负矩阵**
|
**例:假设我们有一个 $3 \times 3$ 对称非负矩阵**
|
||||||
@ -697,22 +707,6 @@ $$
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
#### 疑问
|
|
||||||
|
|
||||||
**!!!为什么采用SNMF?**
|
|
||||||
|
|
||||||
得到可解释、非负的低维表示 $U$
|
|
||||||
|
|
||||||
卡尔曼滤波得到的特征值和特征向量存在噪声 直接进行谱分解重构会导致重构出来的矩阵不满足对称性。但是SNMF在迭代的过程中增加了**非负**且**对称**的约束!
|
|
||||||
|
|
||||||
可以确保 $A' = UU^{\mathsf T}$ 得到的重构矩阵是对称且非负的!!!
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
#### **时间复杂度分析**
|
#### **时间复杂度分析**
|
||||||
|
|
||||||
(1) 初始构造阶段(假设特征值 特征向量已提前获取,不做分析)
|
(1) 初始构造阶段(假设特征值 特征向量已提前获取,不做分析)
|
||||||
|
|||||||
@ -215,17 +215,14 @@ public class Order { // ← 聚合根(Aggregate Root)
|
|||||||
**特征**
|
**特征**
|
||||||
|
|
||||||
- 封装持久化操作:Repository负责封装所有与数据源交互的操作,如**创建、读取、更新和删除(CRUD)操作**。这样,领域层的代码就可以避免直接处理数据库或其他存储机制的复杂性。
|
- 封装持久化操作:Repository负责封装所有与数据源交互的操作,如**创建、读取、更新和删除(CRUD)操作**。这样,领域层的代码就可以避免直接处理数据库或其他存储机制的复杂性。
|
||||||
- 领域对象的集合管理:Repository通常被视为领域对象的集合,提供了查询和过滤这些对象的方法,使得领域对象的获取和管理更加方便。
|
|
||||||
- 抽象接口:Repository定义了一个与持久化机制无关的接口,这使得领域层的代码可以在不同的持久化机制之间切换,而不需要修改业务逻辑。
|
- 抽象接口:Repository定义了一个与持久化机制无关的接口,这使得领域层的代码可以在不同的持久化机制之间切换,而不需要修改业务逻辑。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**职责分离**
|
**职责分离**
|
||||||
|
|
||||||
- **领域层** 只定义 **Repository 接口**,关注“需要做哪些数据操作”(增删改查、复杂查询),不关心具体实现。
|
- **领域层** 只定义 **Repository 接口**,关注“需要做哪些数据操作”(增删改查、复杂查询),不关心具体实现。
|
||||||
- **基础设施层** 实现这些接口(ORM、JDBC、Redis、ES、RPC、HTTP、MQ 推送等),封装所有外部资源的访问细节。
|
- **基础设施层** 实现这些接口(ORM、JDBC、Redis、ES、RPC、HTTP、MQ 推送等),封装所有外部资源的访问细节。
|
||||||
|
|
||||||
仓储解耦的手段使用了依赖倒置的设计。
|
仓储解耦的手段使用了**依赖倒置**的设计。
|
||||||
|
|
||||||
<img src="https://pic.bitday.top/i/2025/06/25/qt4nbs-0.png" alt="image-20250625162115367" style="zoom: 80%;" />
|
<img src="https://pic.bitday.top/i/2025/06/25/qt4nbs-0.png" alt="image-20250625162115367" style="zoom: 80%;" />
|
||||||
|
|
||||||
@ -241,17 +238,29 @@ public interface IActivityRepository {
|
|||||||
}
|
}
|
||||||
```
|
```
|
||||||
|
|
||||||
|
**使用:**在应用程序中使用**依赖注入**(DI)来将具体的Repository实现注入到需要它们的领域服务或应用服务中。
|
||||||
|
|
||||||
|
|
||||||
### 聚合和领域服务的区别
|
|
||||||
|
|
||||||
| 特性 | 聚合(Aggregate) | 领域服务(Domain Service) |
|
### 聚合和领域服务和仓储服务的比较
|
||||||
| ------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
|
|
||||||
| **本质** | **一组相关**实体和值对象的组合,形成一个事务与一致性边界 | 无状态的业务逻辑单元,封装**跨实体或跨聚合**的操作 |
|
| 特性 | **聚合(Aggregate)** | **领域服务(Domain Service)** | **仓储(Repository)** |
|
||||||
| **状态** | 有状态——包含实体/值对象,维护自身的数据和不变式 | 无状态——只定义行为,不保存对象状态 |
|
| ------------ | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
|
||||||
| **职责** | 1. 维护内部对象的一致性2. 提供对外唯一入口(聚合根)3. 定义事务边界 | 1. 执行不适合归入任何单一聚合的方法2. 协调多个聚合或实体完成一段业务流程 |
|
| **本质** | 相关**实体和值对象的组合**,以“聚合根”为唯一访问入口 | 无状态的**业务逻辑单元**,封装**跨实体 / 跨聚合**规则 | 抽象的数据访问接口,隐藏底层存储细节,为聚合**提供持久化能力** |
|
||||||
| **边界** | 聚合边界内的所有操作要么全部成功要么全部失败 | 没有一致性边界,只是一段可复用的业务流程 |
|
| **状态** | **有状态**——内部维护数据与不变式 | **无状态**——仅暴露行为 | **无业务状态**;实现层可能有缓存,但对外看作无状态 |
|
||||||
| **典型用法** | `Order.addItem()`、`Order.updateAddress()` 等,操作聚合根来修改内部状态 | `PricingService.calculateFinalPrice(order, coupons)`<br />`InventoryService.reserveStock(order)` |
|
| **职责** | 1. 内部一致性2. 定义事务边界3. 提供领域行为(`order.pay()` 等) | 1. 承载跨实体规则2. 协调多个聚合完成业务动作 | 1. 加载 / 保存聚合根2. 把 PO ↔️ Entity 映射3. 屏蔽 SQL/ORM/缓存等技术细节 |
|
||||||
|
| **边界** | *聚合边界*:内部操作要么全部成功要么全部失败 | 无一致性边界,仅调用聚合或仓储 | *持久化边界*:一次操作针对一个聚合;不负责业务事务(由应用层控制) |
|
||||||
|
| **典型用法** | `Order.addItem()`,`Order.cancel()` | `PricingService.calculate(...)`,`InventoryService.reserveStock(...)` | `orderRepository.findById(id)`,`orderRepository.save(order)` |
|
||||||
|
|
||||||
|
**自己总结:**领域服务纯写业务逻辑并注入仓储服务;
|
||||||
|
|
||||||
|
仓储服务只写接口,规定一个具体的'动作';
|
||||||
|
|
||||||
|
然后基础设施层中子类实现该仓储接口,并注入若干Dao,一个'动作'可能调用多个Dao来实现;
|
||||||
|
|
||||||
|
Dao直接与数据库打交道,实现增删查改。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
@ -11,8 +11,8 @@ Intellij Ideav创建Java项目:
|
|||||||
|
|
||||||
IDEA快捷键:
|
IDEA快捷键:
|
||||||
|
|
||||||
| `Ctrl + Alt + L` | 格式化代码 |
|
| `Ctrl + L` | 格式化代码 |
|
||||||
| ---------------- | ------------------------- |
|
| ------------- | ------------------------- |
|
||||||
| `Ctrl + /` | 注释/取消注释当前行 |
|
| `Ctrl + /` | 注释/取消注释当前行 |
|
||||||
| `Ctrl + D` | 复制当前行或选中的代码块 |
|
| `Ctrl + D` | 复制当前行或选中的代码块 |
|
||||||
| `Ctrl + Y` | 删除当前行 |
|
| `Ctrl + Y` | 删除当前行 |
|
||||||
@ -1859,6 +1859,8 @@ public @interface MyAnnotation {
|
|||||||
|
|
||||||
@Target(ElementType.TYPE) //类上的注解(包含类、接口、枚举等类型)
|
@Target(ElementType.TYPE) //类上的注解(包含类、接口、枚举等类型)
|
||||||
|
|
||||||
|
@Target(ElementType.FIELD) //字段上的注解
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**简化使用**:如果注解中只有一个属性需要设置,而且该属性名为 `value`,则在使用时可以省略属性名
|
**简化使用**:如果注解中只有一个属性需要设置,而且该属性名为 `value`,则在使用时可以省略属性名
|
||||||
|
|||||||
@ -1016,50 +1016,43 @@ Integer top = stack.pop(); // 出栈
|
|||||||
- `offerFirst(E e)`:**在队头插入元素**,返回 `true` 或 `false` 表示是否成功。
|
- `offerFirst(E e)`:**在队头插入元素**,返回 `true` 或 `false` 表示是否成功。
|
||||||
- `peekFirst()`:查看队头元素,不移除;队列为空返回 `null`。
|
- `peekFirst()`:查看队头元素,不移除;队列为空返回 `null`。
|
||||||
- `pollFirst()`:移除并返回队头元素;队列为空返回 `null`。
|
- `pollFirst()`:移除并返回队头元素;队列为空返回 `null`。
|
||||||
|
- `poll()` :移除并返回队头元素
|
||||||
|
|
||||||
*在队尾操作*
|
*在队尾操作*
|
||||||
|
|
||||||
- `offerLast(E e)`:在队尾插入元素,返回 `true` 或 `false` 表示是否成功。
|
- `offerLast(E e)`:在队尾插入元素,返回 `true` 或 `false` 表示是否成功。
|
||||||
|
- `offer(E e)` : 把元素放到 队尾
|
||||||
- `peekLast()`:查看队尾元素,不移除;队列为空返回 `null`。
|
- `peekLast()`:查看队尾元素,不移除;队列为空返回 `null`。
|
||||||
- `pollLast()`:移除并返回队尾元素;队列为空返回 `null`。
|
- `pollLast()`:移除并返回队尾元素;队列为空返回 `null`。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
*添加元素*:调用 `offer(e)` 时,实际上是调用 `offerLast(e)`,即在**队尾**添加元素。push(e)` ⇒ 等价于 `addFirst(e)
|
|
||||||
|
|
||||||
*删除或查看元素*:调用`poll()` 时,则是调用 `pollFirst()`,即在队头移除元素;同理, `peek()` 则是查看队头元素。
|
|
||||||
|
|
||||||
```java
|
```java
|
||||||
import java.util.Deque;
|
import java.util.Deque;
|
||||||
import java.util.ArrayDeque;
|
import java.util.ArrayDeque;
|
||||||
|
|
||||||
public class DequeExample {
|
public class DequeExampleSafe {
|
||||||
public static void main(String[] args) {
|
public static void main(String[] args) {
|
||||||
// 使用 ArrayDeque 实现双端队列
|
// 使用 ArrayDeque 实现双端队列
|
||||||
Deque<Integer> deque = new ArrayDeque<>();
|
Deque<Integer> deque = new ArrayDeque<>();
|
||||||
|
|
||||||
// 在队列头部添加元素
|
/* ========= 在队列两端“安全”地添加元素 ========= */
|
||||||
deque.addFirst(10);
|
deque.offerFirst(10); // 队头 ← 10
|
||||||
// 在队列尾部添加元素
|
deque.offerLast(20); // 20 ← 队尾
|
||||||
deque.addLast(20);
|
deque.offerFirst(5); // 队头 ← 5,10,20
|
||||||
// 在队列头部插入元素(和 addFirst 类似,但失败时不会抛异常)
|
deque.offerLast(30); // 队尾 → 5,10,20,30
|
||||||
deque.offerFirst(5);
|
|
||||||
// 在队列尾部插入元素
|
|
||||||
deque.offerLast(30);
|
|
||||||
|
|
||||||
System.out.println("双端队列内容:" + deque);
|
System.out.println("双端队列内容:" + deque);
|
||||||
|
|
||||||
// 查看队头和队尾元素,不移除
|
/* ========= “安全”地查看队头/队尾 ========= */
|
||||||
int first = deque.peekFirst();
|
Integer first = deque.peekFirst(); // 队头元素(5)
|
||||||
int last = deque.peekLast();
|
Integer last = deque.peekLast(); // 队尾元素(30)
|
||||||
System.out.println("队头元素:" + first);
|
System.out.println("队头元素:" + first);
|
||||||
System.out.println("队尾元素:" + last);
|
System.out.println("队尾元素:" + last);
|
||||||
|
|
||||||
// 从队头移除元素
|
/* ========= “安全”地移除队头/队尾 ========= */
|
||||||
int removedFirst = deque.removeFirst();
|
Integer removedFirst = deque.pollFirst(); // 移除并返回队头(5)
|
||||||
System.out.println("移除队头元素:" + removedFirst);
|
System.out.println("移除队头元素:" + removedFirst);
|
||||||
// 从队尾移除元素
|
|
||||||
int removedLast = deque.removeLast();
|
Integer removedLast = deque.pollLast(); // 移除并返回队尾(30)
|
||||||
System.out.println("移除队尾元素:" + removedLast);
|
System.out.println("移除队尾元素:" + removedLast);
|
||||||
|
|
||||||
System.out.println("双端队列最终内容:" + deque);
|
System.out.println("双端队列最终内容:" + deque);
|
||||||
@ -1069,6 +1062,16 @@ public class DequeExample {
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
**栈和双端队列的对应关系**
|
||||||
|
|
||||||
|
栈只有队头!
|
||||||
|
|
||||||
|
* 添加元素:push(e) ⇒ addFirst(e) (安全版:offerFirst(e))
|
||||||
|
* 删除元素:pop() ⇒ removeFirst() (安全版:pollFirst())
|
||||||
|
* 查看栈顶:peek() ⇒ peekFirst()
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### Iterator
|
### Iterator
|
||||||
|
|
||||||
- **`HashMap`、`HashSet`、`ArrayList` 和 `PriorityQueue`** 都实现了 `Iterable` 接口,支持 `iterator()` 方法。
|
- **`HashMap`、`HashSet`、`ArrayList` 和 `PriorityQueue`** 都实现了 `Iterable` 接口,支持 `iterator()` 方法。
|
||||||
@ -1219,6 +1222,8 @@ public void bubbleSort(int[] arr){
|
|||||||
|
|
||||||
### 归并排序
|
### 归并排序
|
||||||
|
|
||||||
|
#### **数组归并排序**
|
||||||
|
|
||||||
**基本思想:**
|
**基本思想:**
|
||||||
|
|
||||||
将待排序的数组视为多个有序子表,每个子表的长度为 1,通过两两归并逐步合并成一个有序数组。
|
将待排序的数组视为多个有序子表,每个子表的长度为 1,通过两两归并逐步合并成一个有序数组。
|
||||||
@ -1288,6 +1293,51 @@ public class MergeSort {
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
#### 链表归并排序
|
||||||
|
|
||||||
|
```java
|
||||||
|
// 简易链表归并排序示意
|
||||||
|
ListNode sortList(ListNode head) {
|
||||||
|
if (head == null || head.next == null) return head;
|
||||||
|
// ① 快慢指针找中点并断链
|
||||||
|
ListNode slow = head, fast = head.next;
|
||||||
|
while (fast != null && fast.next != null) {
|
||||||
|
slow = slow.next;
|
||||||
|
fast = fast.next.next;
|
||||||
|
}
|
||||||
|
ListNode mid = slow.next;
|
||||||
|
slow.next = null;
|
||||||
|
// ② 递归排序左右两段
|
||||||
|
ListNode left = sortList(head);
|
||||||
|
ListNode right = sortList(mid);
|
||||||
|
// ③ 合并
|
||||||
|
return merge(left, right);
|
||||||
|
}
|
||||||
|
|
||||||
|
ListNode merge(ListNode a, ListNode b) {
|
||||||
|
ListNode dummy = new ListNode(-1), p = dummy;
|
||||||
|
while (a != null && b != null) {
|
||||||
|
if (a.val <= b.val) { p.next = a; a = a.next; }
|
||||||
|
else { p.next = b; b = b.next; }
|
||||||
|
p = p.next;
|
||||||
|
}
|
||||||
|
p.next = (a != null ? a : b);
|
||||||
|
return dummy.next;
|
||||||
|
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
**快慢指针找 “中点” 和找 “环” 的出发点为什么会不一样?**
|
||||||
|
|
||||||
|
| 目标 | 常见写法 | **为什么这么设** | 若改成另一种写法会怎样 |
|
||||||
|
| -------------------------------------- | ------------------------------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
|
||||||
|
| **拆链/找中点**(归并排序、回文检测等) | `slow = head`<br />`fast = head.next` | - **偶数长度更均匀**: *len = 4* → 最终 `slow` 停在第 2 个结点(左半长 2,右半长 2)- `mid = slow.next` 一定非 null(当链长 ≥ 2),递归不会拿到空指针 | - `fast = head` 时 *len = 4* → `slow` 停在第 3 个结点(左半长 3,右半长 1),越分越偏; *len = 2* → 左 1 右 0,也能跑,但更不平衡 |
|
||||||
|
| **检测环** | `slow = head`<br />`fast = head` | - 只要两指针步幅不同,就会在环内相遇;- 起点放哪都行,写成同一起点最直观,也少一次空指针判断 | 如果写成 `fast = head.next` 也能检测环,但需先判断 `head.next` 是否为空,代码更啰嗦;并且两指针初始就“错开一步”,相遇时步数不同,求环长或入环点时要再做偏移 |
|
||||||
|
|
||||||
|
总之:自己模拟一遍,奇数和偶数的情况。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 数组排序
|
### 数组排序
|
||||||
|
|
||||||
默认升序:
|
默认升序:
|
||||||
@ -1676,7 +1726,6 @@ public void inOrderTraversalIterative(TreeNode root, List<Integer> list) {
|
|||||||
curr = curr.right;
|
curr = curr.right;
|
||||||
}
|
}
|
||||||
}
|
}
|
||||||
|
|
||||||
```
|
```
|
||||||
|
|
||||||
*迭代法前序*
|
*迭代法前序*
|
||||||
|
|||||||
417
自学/拼团交易系统.md
417
自学/拼团交易系统.md
@ -105,7 +105,7 @@ crowd_tags_job 人群标签任务
|
|||||||
|
|
||||||
**(二)参与拼团表**
|
**(二)参与拼团表**
|
||||||
|
|
||||||
group_buy_account 拼团账户
|
**group_buy_account 拼团账户**
|
||||||
|
|
||||||
| 字段名 | 说明 |
|
| 字段名 | 说明 |
|
||||||
| --------------------- | ------------ |
|
| --------------------- | ------------ |
|
||||||
@ -117,45 +117,50 @@ group_buy_account 拼团账户
|
|||||||
| create_time | 创建时间 |
|
| create_time | 创建时间 |
|
||||||
| update_time | 更新时间 |
|
| update_time | 更新时间 |
|
||||||
|
|
||||||
group_buy_order 用户拼单
|
**group_buy_order 用户拼单**
|
||||||
|
|
||||||
|
一条记录 = 一个拼团**团队**(`team_id` 唯一)
|
||||||
|
|
||||||
| 字段名 | 说明 |
|
| 字段名 | 说明 |
|
||||||
| ---------------------- | ------------------------ |
|
| --------------- | -------------------------------- |
|
||||||
| id | 自增ID |
|
| id | 自增ID |
|
||||||
|
| team_id | 拼单组队ID |
|
||||||
| activity_id | 活动ID |
|
| activity_id | 活动ID |
|
||||||
| group_order_id | 拼单ID 【多少人参与】 |
|
| source | 渠道 |
|
||||||
| group_order_start_time | 拼单开始时间 |
|
| channel | 来源 |
|
||||||
| group_order_end_time | 拼单结束时间 |
|
|
||||||
| source | 来源 |
|
|
||||||
| channel | 渠道 |
|
|
||||||
| goods_id | 商品ID |
|
|
||||||
| original_price | 原始价格 |
|
| original_price | 原始价格 |
|
||||||
| deduction_price | 抵扣价格(各类优惠加成) |
|
| deduction_price | 折扣金额 |
|
||||||
| pay_amount | 实际支付价格 |
|
| pay_price | 支付价格 |
|
||||||
| target_count | 目标数量 |
|
| target_count | 目标数量 |
|
||||||
| complete_count | 完成数量 |
|
| complete_count | 完成数量 |
|
||||||
| status | 状态(拼单中/完成/失败) |
|
| status | 状态(0-拼单中、1-完成、2-失败) |
|
||||||
| notify_url | 回调接口 |
|
|
||||||
| create_time | 创建时间 |
|
| create_time | 创建时间 |
|
||||||
| update_time | 更新时间 |
|
| update_time | 更新时间 |
|
||||||
|
|
||||||
group_buy_order_list 用户拼单明细
|
**group_buy_order_list 用户拼单明细**
|
||||||
|
|
||||||
|
一条记录 = **某用户**在该团队里锁的一笔单
|
||||||
|
|
||||||
| 字段名 | 说明 |
|
| 字段名 | 说明 |
|
||||||
| -------------- | ---------------------- |
|
| --------------- | ------------------------------------ |
|
||||||
| id | |
|
| id | 自增ID |
|
||||||
|
| user_id | 用户ID |
|
||||||
|
| team_id | 拼单组队ID |
|
||||||
|
| order_id | 订单ID |
|
||||||
| activity_id | 活动ID |
|
| activity_id | 活动ID |
|
||||||
| group_order_id | 拼单ID |
|
| start_time | 活动开始时间 |
|
||||||
| user_id | 用户id |
|
| end_time | 活动结束时间 |
|
||||||
| user_type | 团长/团员 |
|
|
||||||
| source | 来源 |
|
|
||||||
| channel | 渠道 |
|
|
||||||
| goods_id | 商品ID |
|
| goods_id | 商品ID |
|
||||||
| out_trade_no | 外部交易单号,唯一幂等 |
|
| source | 渠道 |
|
||||||
|
| channel | 来源 |
|
||||||
|
| original_price | 原始价格 |
|
||||||
|
| deduction_price | 折扣金额 |
|
||||||
|
| status | 状态;0 初始锁定、1 消费完成 |
|
||||||
|
| out_trade_no | 外部交易单号(确保外部调用唯一幂等) |
|
||||||
| create_time | 创建时间 |
|
| create_time | 创建时间 |
|
||||||
| update_time | 更新时间 |
|
| update_time | 更新时间 |
|
||||||
|
|
||||||
notify_task 回调任务
|
**notify_task 回调任务**
|
||||||
|
|
||||||
| 字段名 | 说明 |
|
| 字段名 | 说明 |
|
||||||
| -------------- | ---------------------------------- |
|
| -------------- | ---------------------------------- |
|
||||||
@ -278,8 +283,54 @@ EndNode.apply() → 组装结果并返回 TrialBalanceEntity
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
## 拼团交易锁单
|
||||||
|
|
||||||
|
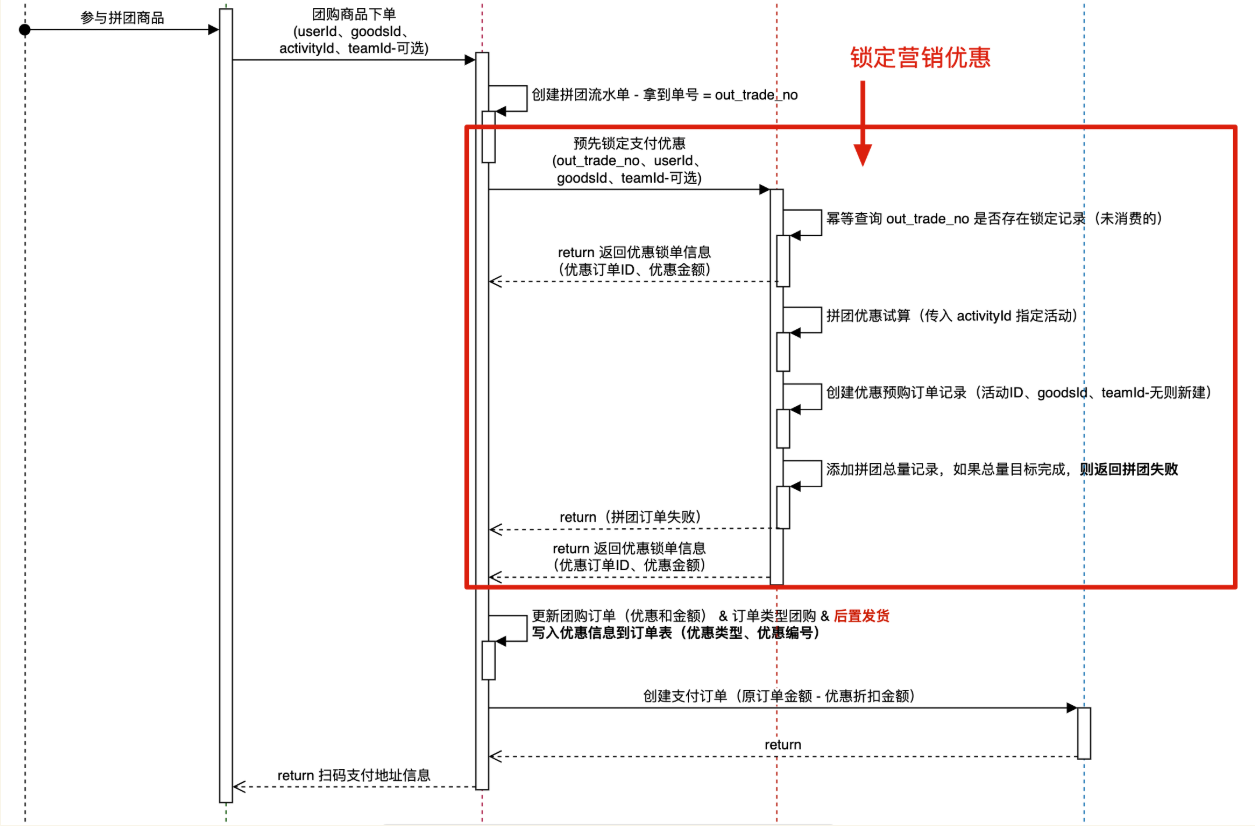
|
||||||
|
|
||||||
|
下单到支付中间有一个流程,即锁单,比如淘宝京东中,在这个环节(限定时间内)选择使用优惠券、京豆等,可以得到优惠价,再进行支付;拼团场景同理,先加入拼团,进行锁单,然后优惠试算,最后才付款。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 收获
|
## 收获
|
||||||
|
|
||||||
|
### 实体对象
|
||||||
|
|
||||||
|
实体是指具有唯一标识的业务对象。
|
||||||
|
|
||||||
|
在 DDD 分层里,**Domain Entity ≠ 数据库 PO**。
|
||||||
|
在 `edu.whut.domain.*.model.entity` 包下放的是**纯粹的业务对象**,它们只表达业务语义(团队 ID、活动时间、优惠金额……),对「数据持久化细节」保持**无感知**。因此它们看起来“字段不全”是正常的:
|
||||||
|
|
||||||
|
- 它们不会带 `@TableName` / `@TableId` 等 MyBatis-Plus 注解;
|
||||||
|
- 也不会出现数据库的技术字段(`id`、`create_time`、`update_time`、`status` 等);
|
||||||
|
- 只保留聚合根真正**需要的**业务属性与行为。
|
||||||
|
|
||||||
|
```java
|
||||||
|
@Data
|
||||||
|
@Builder
|
||||||
|
@AllArgsConstructor
|
||||||
|
@NoArgsConstructor
|
||||||
|
public class PayActivityEntity {
|
||||||
|
|
||||||
|
/** 拼单组队ID */
|
||||||
|
private String teamId;
|
||||||
|
/** 活动ID */
|
||||||
|
private Long activityId;
|
||||||
|
/** 活动名称 */
|
||||||
|
private String activityName;
|
||||||
|
/** 拼团开始时间 */
|
||||||
|
private Date startTime;
|
||||||
|
/** 拼团结束时间 */
|
||||||
|
private Date endTime;
|
||||||
|
/** 目标数量 */
|
||||||
|
private Integer targetCount;
|
||||||
|
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
这个也是实体对象,因为多个字段的组合:teamId和activityId能唯一标识这个实体。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 模板方法
|
### 模板方法
|
||||||
|
|
||||||
**核心思想**:
|
**核心思想**:
|
||||||
@ -366,6 +417,229 @@ public class Demo {
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 责任链
|
||||||
|
|
||||||
|
应用场景:日志系统、审批流程、权限校验——任何需要将请求按阶段传递、并由某一环节决定是否继续或终止处理的地方,都非常适合职责链模式。
|
||||||
|
|
||||||
|
#### 单例链
|
||||||
|
|
||||||
|
典型的责任链模式要点:
|
||||||
|
|
||||||
|
- **解耦请求发送者和处理者**:调用者只持有链头,不关心中间环节。
|
||||||
|
- **动态组装**:通过 `appendNext` 可以灵活地增加、删除或重排链上的节点。
|
||||||
|
- **可扩展**:新增处理逻辑只需继承 `AbstractLogicLink` 并实现 `apply`,不用改动已有代码。
|
||||||
|
|
||||||
|
接口定义:`ILogicChainArmory<T, D, R>` 提供添加节点方法和获取节点
|
||||||
|
|
||||||
|
```java
|
||||||
|
//定义了责任链的组装接口:
|
||||||
|
public interface ILogicChainArmory<T, D, R> {
|
||||||
|
|
||||||
|
ILogicLink<T, D, R> next(); //在当前节点中获取下一个节点
|
||||||
|
|
||||||
|
ILogicLink<T, D, R> appendNext(ILogicLink<T, D, R> next); //把下一个处理节点挂接上来
|
||||||
|
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
`ILogicLink<T, D, R>` 继承自 `ILogicChainArmory<T, D, R>`,并额外声明了核心方法 `apply`
|
||||||
|
|
||||||
|
```java
|
||||||
|
public interface ILogicLink<T, D, R> extends ILogicChainArmory<T, D, R> {
|
||||||
|
|
||||||
|
R apply(T requestParameter, D dynamicContext) throws Exception; //处理请求
|
||||||
|
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
抽象基类:`AbstractLogicLink`
|
||||||
|
|
||||||
|
```java
|
||||||
|
public abstract class AbstractLogicLink<T, D, R> implements ILogicLink<T, D, R> {
|
||||||
|
|
||||||
|
private ILogicLink<T, D, R> next;
|
||||||
|
|
||||||
|
@Override
|
||||||
|
public ILogicLink<T, D, R> next() {
|
||||||
|
return next;
|
||||||
|
}
|
||||||
|
|
||||||
|
@Override
|
||||||
|
public ILogicLink<T, D, R> appendNext(ILogicLink<T, D, R> next) {
|
||||||
|
this.next = next;
|
||||||
|
return next;
|
||||||
|
}
|
||||||
|
|
||||||
|
protected R next(T requestParameter, D dynamicContext) throws Exception {
|
||||||
|
return next.apply(requestParameter, dynamicContext); //交给下一节点处理
|
||||||
|
}
|
||||||
|
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
子类只需继承它,重写 `apply(...)`,在合适的条件下要么直接处理并返回,要么调用 `next(requestParameter, dynamicContext)` 继续传递。
|
||||||
|
|
||||||
|
**使用示例:**
|
||||||
|
|
||||||
|
```java
|
||||||
|
public class AuthLink extends AbstractLogicLink<Request, Context, Response> {
|
||||||
|
@Override
|
||||||
|
public Response apply(Request req, Context ctx) throws Exception {
|
||||||
|
if (!ctx.isAuthenticated()) {
|
||||||
|
throw new UnauthorizedException();
|
||||||
|
}
|
||||||
|
// 认证通过,继续下一个环节
|
||||||
|
return next(req, ctx);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
public class LoggingLink extends AbstractLogicLink<Request, Context, Response> {
|
||||||
|
@Override
|
||||||
|
public Response apply(Request req, Context ctx) throws Exception {
|
||||||
|
System.out.println("Request received: " + req);
|
||||||
|
Response resp = next(req, ctx);
|
||||||
|
System.out.println("Response sent: " + resp);
|
||||||
|
return resp;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
// 组装责任链 放工厂类factory中实现
|
||||||
|
ILogicLink<Request, Context, Response> chain =
|
||||||
|
new AuthLink()
|
||||||
|
.appendNext(new LoggingLink())
|
||||||
|
.appendNext(new BusinessLogicLink());
|
||||||
|
|
||||||
|
//客户端使用
|
||||||
|
Request req = new Request(...);
|
||||||
|
Context ctx = new Context(...);
|
||||||
|
Response resp = chain.apply(req, ctx);
|
||||||
|
```
|
||||||
|
|
||||||
|
示例图:
|
||||||
|
|
||||||
|
```text
|
||||||
|
AuthLink.apply
|
||||||
|
└─▶ LoggingLink.apply
|
||||||
|
└─▶ BusinessLogicLink.apply
|
||||||
|
└─▶ 返回 Response
|
||||||
|
```
|
||||||
|
|
||||||
|
这种模式链上的每个节点都手动 `next()`到下一节点。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
#### 多例链
|
||||||
|
|
||||||
|
```java
|
||||||
|
/**
|
||||||
|
* 通用逻辑处理器接口 —— 责任链中的「节点」要实现的核心契约。
|
||||||
|
*/
|
||||||
|
public interface ILogicHandler<T, D, R> {
|
||||||
|
|
||||||
|
/**
|
||||||
|
* 默认的 next占位实现,方便节点若不需要向后传递时直接返回 null。
|
||||||
|
*/
|
||||||
|
default R next(T requestParameter, D dynamicContext) {
|
||||||
|
return null;
|
||||||
|
}
|
||||||
|
|
||||||
|
/**
|
||||||
|
* 节点的核心处理方法。
|
||||||
|
*/
|
||||||
|
R apply(T requestParameter, D dynamicContext) throws Exception;
|
||||||
|
|
||||||
|
}
|
||||||
|
|
||||||
|
```
|
||||||
|
|
||||||
|
```java
|
||||||
|
/**
|
||||||
|
* 业务链路容器 —— 双向链表实现,同时实现 ILogicHandler,从而可以被当作单个节点使用。
|
||||||
|
*/
|
||||||
|
public class BusinessLinkedList<T, D, R> extends LinkedList<ILogicHandler<T, D, R>> implements ILogicHandler<T, D, R>{
|
||||||
|
|
||||||
|
public BusinessLinkedList(String name) {
|
||||||
|
super(name);
|
||||||
|
}
|
||||||
|
|
||||||
|
/**
|
||||||
|
* BusinessLinkedList是头节点,它的apply方法就是循环调用后面的节点,直至返回。
|
||||||
|
* 遍历并执行链路。
|
||||||
|
*/
|
||||||
|
@Override
|
||||||
|
public R apply(T requestParameter, D dynamicContext) throws Exception {
|
||||||
|
Node<ILogicHandler<T, D, R>> current = this.first;
|
||||||
|
// 顺序执行,直到链尾或返回结果
|
||||||
|
while (current != null) {
|
||||||
|
ILogicHandler<T, D, R> handler = current.item;
|
||||||
|
R result = handler.apply(requestParameter, dynamicContext);
|
||||||
|
if (result != null) {
|
||||||
|
// 节点命中,立即返回
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
//result==null,则交给那一节点继续处理
|
||||||
|
current = current.next;
|
||||||
|
}
|
||||||
|
// 全链未命中
|
||||||
|
return null;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
```java
|
||||||
|
/**
|
||||||
|
* 链路装配工厂 —— 负责把一组 ILogicHandler 顺序注册到 BusinessLinkedList 中。
|
||||||
|
*/
|
||||||
|
public class LinkArmory<T, D, R> {
|
||||||
|
|
||||||
|
private final BusinessLinkedList<T, D, R> logicLink;
|
||||||
|
|
||||||
|
/**
|
||||||
|
* @param linkName 链路名称,便于日志排查
|
||||||
|
* @param logicHandlers 节点列表,按传入顺序链接
|
||||||
|
*/
|
||||||
|
@SafeVarargs
|
||||||
|
public LinkArmory(String linkName, ILogicHandler<T, D, R>... logicHandlers) {
|
||||||
|
logicLink = new BusinessLinkedList<>(linkName);
|
||||||
|
for (ILogicHandler<T, D, R> logicHandler: logicHandlers){
|
||||||
|
logicLink.add(logicHandler);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
/** 返回组装完成的链路 */
|
||||||
|
public BusinessLinkedList<T, D, R> getLogicLink() {
|
||||||
|
return logicLink;
|
||||||
|
}
|
||||||
|
|
||||||
|
}
|
||||||
|
|
||||||
|
//工厂类,可以定义多条责任链,每条有自己的Bean名称区分。
|
||||||
|
@Bean("tradeRuleFilter")
|
||||||
|
public BusinessLinkedList<TradeRuleCommandEntity, DynamicContext, TradeRuleFilterBackEntity> tradeRuleFilter(ActivityUsabilityRuleFilter activityUsabilityRuleFilter, UserTakeLimitRuleFilter userTakeLimitRuleFilter) {
|
||||||
|
// 1. 组装链
|
||||||
|
LinkArmory<TradeRuleCommandEntity, DynamicContext, TradeRuleFilterBackEntity> linkArmory =
|
||||||
|
new LinkArmory<>("交易规则过滤链", activityUsabilityRuleFilter, userTakeLimitRuleFilter);
|
||||||
|
|
||||||
|
// 2. 返回链容器(即可作为责任链使用)
|
||||||
|
return linkArmory.getLogicLink();
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
示例图:
|
||||||
|
|
||||||
|
```text
|
||||||
|
BusinessLinkedList.apply ←─ 只有这一层在栈里
|
||||||
|
while 循环:
|
||||||
|
├─▶ 调用 ActivityUsability.apply → 返回 null → 继续
|
||||||
|
├─▶ 调用 UserTakeLimit.apply → 返回 null → 继续
|
||||||
|
└─▶ 调用 ... → 返回 Result → break
|
||||||
|
|
||||||
|
```
|
||||||
|
|
||||||
|
链头拿着“游标”一个个跑,节点只告诉“命中 / 未命中”。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 规则树流程
|
### 规则树流程
|
||||||
|
|
||||||
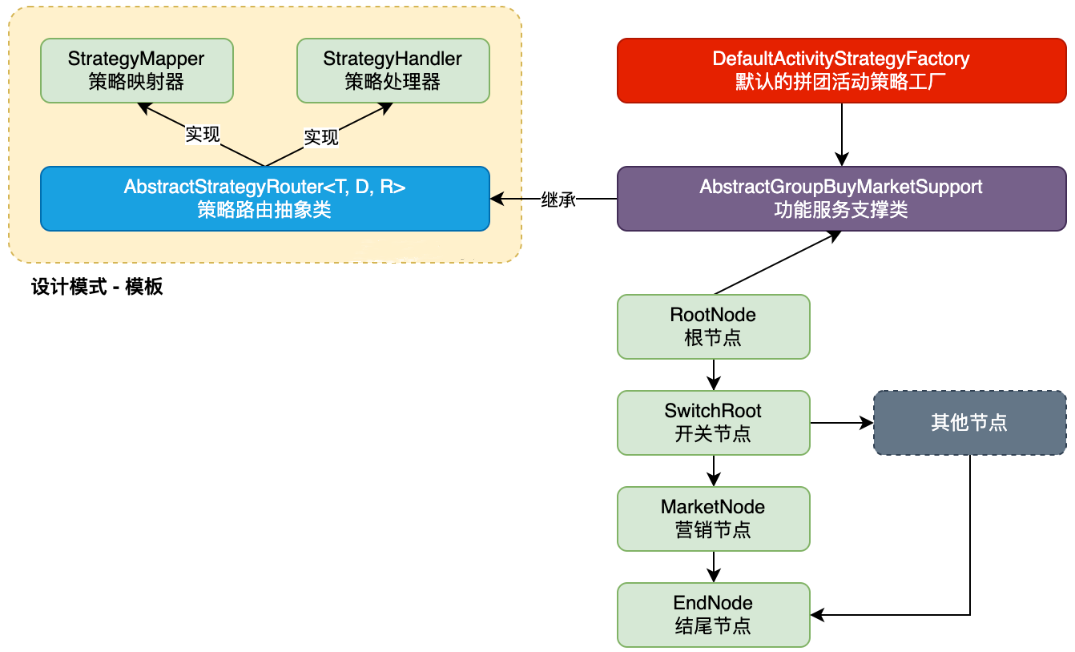
|

|
||||||
@ -502,6 +776,8 @@ public class DiscountContext {
|
|||||||
|
|
||||||
### 多线程异步调用
|
### 多线程异步调用
|
||||||
|
|
||||||
|
如果某任务比较耗时(如加载大量数据),可以考虑开多线程异步调用。
|
||||||
|
|
||||||
```java
|
```java
|
||||||
// Runnable ➞ 只能 run(),没有返回值
|
// Runnable ➞ 只能 run(),没有返回值
|
||||||
public interface Runnable {
|
public interface Runnable {
|
||||||
@ -551,7 +827,7 @@ public class SimpleAsyncDemo {
|
|||||||
// 主线程可以先做别的事…
|
// 主线程可以先做别的事…
|
||||||
System.out.println("主线程正在做其他事情…");
|
System.out.println("主线程正在做其他事情…");
|
||||||
|
|
||||||
// ③ 在需要的时候再获取结果(可加超时)
|
// 在需要的时候再获取结果(可加超时)
|
||||||
String result1 = future1.get(1, TimeUnit.SECONDS); //设置超时时间1秒
|
String result1 = future1.get(1, TimeUnit.SECONDS); //设置超时时间1秒
|
||||||
String result2 = future2.get(); //无超时时间
|
String result2 = future2.get(); //无超时时间
|
||||||
|
|
||||||
@ -571,3 +847,96 @@ public class SimpleAsyncDemo {
|
|||||||
}
|
}
|
||||||
```
|
```
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 动态配置(热更新)
|
||||||
|
|
||||||
|
**注解标记**
|
||||||
|
用 `@DCCValue("key:default")` 标注需要动态注入的字段,指定对应的 Redis Key(带前缀)及默认值。
|
||||||
|
|
||||||
|
```java
|
||||||
|
// 标记要动态注入的字段
|
||||||
|
@Retention(RUNTIME) @Target(FIELD)
|
||||||
|
public @interface DCCValue {
|
||||||
|
String value(); // "key:default"
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
```java
|
||||||
|
// 业务使用示例
|
||||||
|
@Service
|
||||||
|
public class MyFeature {
|
||||||
|
@DCCValue("myFlag:0")
|
||||||
|
private String myFlag;
|
||||||
|
public boolean enabled() { return "1".equals(myFlag); }
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
**启动时注入**
|
||||||
|
实现一个 `BeanPostProcessor`,在每个 Spring Bean 初始化后:
|
||||||
|
|
||||||
|
- 扫描带 `@DCCValue` 的字段;
|
||||||
|
- 拼出完整 Redis Key(如 `dcc_prefix_key`),若不存在则写入默认值,否则读最新值;
|
||||||
|
- 反射把值注入到该 Bean 的私有字段;
|
||||||
|
- 将 `(redisKey → Bean 实例)` 记录到内存映射,用于后续热更新。
|
||||||
|
|
||||||
|
```java
|
||||||
|
@Override
|
||||||
|
public Object postProcessAfterInitialization(Object bean, String name) {
|
||||||
|
Class<?> cls = AopUtils.isAopProxy(bean)
|
||||||
|
? AopUtils.getTargetClass(bean)
|
||||||
|
: bean.getClass();
|
||||||
|
for (Field f : cls.getDeclaredFields()) {
|
||||||
|
DCCValue dv = f.getAnnotation(DCCValue.class);
|
||||||
|
if (dv==null) continue;
|
||||||
|
String[] p = dv.value().split(":");
|
||||||
|
String key = PREFIX + p[0], defaultValue = p[1];
|
||||||
|
RBucket<String> bucket = redis.getBucket(key);
|
||||||
|
String val = bucket.isExists() ? bucket.get() : defaultValue;
|
||||||
|
bucket.trySet(defaultValue); //同步redis内容
|
||||||
|
injectField(bean, f, val); //反射注入
|
||||||
|
beans.put(key, bean);
|
||||||
|
}
|
||||||
|
return bean;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
**运行时热更新**
|
||||||
|
|
||||||
|
- 在同一个组件里,订阅一个 Redis Topic(频道),比如 `"dcc_update"`;
|
||||||
|
|
||||||
|
- 外部调用发布接口 `PUBLISH dcc_update "key,newValue"`;
|
||||||
|
|
||||||
|
```java
|
||||||
|
//更新配置
|
||||||
|
@GetMapping("/dcc/update")
|
||||||
|
public void update(@RequestParam String key, @RequestParam String value) {
|
||||||
|
dccTopic().publish(key + "," + value);
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
- 订阅者收到后:
|
||||||
|
|
||||||
|
1. 同步把新值写回 Redis;
|
||||||
|
2. 从映射里取出对应 Bean,反射更新它的字段。
|
||||||
|
|
||||||
|
```java
|
||||||
|
// 发布/订阅频道
|
||||||
|
@Bean
|
||||||
|
public RTopic dccTopic() {
|
||||||
|
RTopic t = redis.getTopic("dcc_update");
|
||||||
|
t.addListener(String.class, (c,msg)->{
|
||||||
|
String[] a = msg.split(",");
|
||||||
|
String key = PREFIX + a[0], val = a[1];
|
||||||
|
RBucket<String> bucket = redis.getBucket(key);
|
||||||
|
if (!bucket.isExists()) return;
|
||||||
|
bucket.set(val);
|
||||||
|
Object bean = beans.get(key);
|
||||||
|
if (bean!=null) injectField(bean, a[0], val);
|
||||||
|
});
|
||||||
|
return t;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
168
自学/草稿.md
168
自学/草稿.md
@ -1,159 +1,19 @@
|
|||||||
### 一、策略模式 (Strategy)
|
### 聚合 vs 领域服务 vs 仓储 —— 对比一览
|
||||||
|
|
||||||
**核心思想**:
|
| 特性 | **聚合(Aggregate)** | **领域服务(Domain Service)** | **仓储(Repository)** |
|
||||||
把可互换的算法/行为抽成独立策略类,运行时由“上下文”对象选择合适的策略;对调用方来说,只关心统一接口,而非具体实现。
|
| ------------ | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
|
||||||
|
| **本质** | 相关实体和值对象的**组合**,以“聚合根”为唯一访问入口 | 无状态的业务逻辑单元,封装**跨实体 / 跨聚合**规则 | 抽象的数据访问接口,隐藏底层存储细节,为聚合**提供持久化能力** |
|
||||||
|
| **状态** | **有状态**——内部维护数据与不变式 | **无状态**——仅暴露行为 | **无业务状态**;实现层可能有缓存,但对外看作无状态 |
|
||||||
|
| **职责** | 1. 内部一致性2. 定义事务边界3. 提供领域行为(`order.pay()` 等) | 1. 承载跨实体规则2. 协调多个聚合完成业务动作 | 1. 加载 / 保存聚合根2. 把 PO ↔️ Entity 映射3. 屏蔽 SQL/ORM/缓存等技术细节 |
|
||||||
|
| **边界** | *聚合边界*:内部操作要么全部成功要么全部失败 | 无一致性边界,仅调用聚合或仓储 | *持久化边界*:一次操作针对一个聚合;不负责业务事务(由应用层控制) |
|
||||||
|
| **典型用法** | `Order.addItem()`,`Order.cancel()` | `PricingService.calculate(...)`,`InventoryService.reserveStock(...)` | `orderRepository.findById(id)`,`orderRepository.save(order)` |
|
||||||
|
|
||||||
```
|
#### 快速记忆
|
||||||
┌───────────────┐
|
|
||||||
│ Client │
|
|
||||||
└─────▲─────────┘
|
|
||||||
│ has-a
|
|
||||||
┌─────┴─────────┐ implements
|
|
||||||
│ Context │────────────┐ ┌──────────────┐
|
|
||||||
│ (使用者) │ strategy └─▶│ Strategy A │
|
|
||||||
└───────────────┘ ├──────────────┤
|
|
||||||
│ Strategy B │
|
|
||||||
└──────────────┘
|
|
||||||
```
|
|
||||||
|
|
||||||
#### Demo:支付策略(Java)
|
- **聚合**:有数据 + 行为,是“业务发动机”
|
||||||
|
- **领域服务**:无数据,专管“发动机之间的协作”
|
||||||
|
- **仓储**:无业务规则,只负责把“发动机”**存取**到持久化介质
|
||||||
|
|
||||||
```java
|
这样三者的定位就清晰了:
|
||||||
// 1. 抽象策略
|
|
||||||
public interface PayStrategy {
|
|
||||||
void pay(int cents);
|
|
||||||
}
|
|
||||||
|
|
||||||
// 2. 具体策略
|
> “**聚合**管状态,**领域服务**管跨聚合业务,**仓储**管存取。”
|
||||||
public class AliPay implements PayStrategy {
|
|
||||||
public void pay(int cents) { System.out.println("Alipay ¥" + cents / 100.0); }
|
|
||||||
}
|
|
||||||
public class WxPay implements PayStrategy {
|
|
||||||
public void pay(int cents) { System.out.println("WeChat Pay ¥" + cents / 100.0); }
|
|
||||||
}
|
|
||||||
|
|
||||||
// 3. 上下文
|
|
||||||
public class PaymentService {
|
|
||||||
private final PayStrategy strategy;
|
|
||||||
public PaymentService(PayStrategy strategy) { this.strategy = strategy; }
|
|
||||||
public void checkout(int cents) { strategy.pay(cents); }
|
|
||||||
}
|
|
||||||
|
|
||||||
// 4. 运行时选择策略
|
|
||||||
public class Demo {
|
|
||||||
public static void main(String[] args) {
|
|
||||||
PaymentService ps1 = new PaymentService(new AliPay());
|
|
||||||
ps1.checkout(2599); // Alipay ¥25.99
|
|
||||||
|
|
||||||
PaymentService ps2 = new PaymentService(new WxPay());
|
|
||||||
ps2.checkout(4999); // WeChat Pay ¥49.99
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**要点**
|
|
||||||
|
|
||||||
- **开放封闭**:新增 PayPal 只需实现 `PayStrategy`,无须改 `PaymentService`。
|
|
||||||
- **运行期切换**:可根据配置、用户偏好等动态注入不同策略。
|
|
||||||
|
|
||||||
------
|
|
||||||
|
|
||||||
### 二、模板方法模式 (Template Method)
|
|
||||||
|
|
||||||
**核心思想**:
|
|
||||||
在抽象父类中定义**算法骨架**(固定执行顺序),把某些可变步骤留给子类重写;调用方只用模板方法,保证流程一致。
|
|
||||||
|
|
||||||
```
|
|
||||||
Client ───▶ AbstractClass
|
|
||||||
├─ templateMethod() ←—— 固定流程
|
|
||||||
│ step1()
|
|
||||||
│ step2() ←—— 抽象,可变
|
|
||||||
│ step3()
|
|
||||||
└─ hookMethod() ←—— 可选覆盖
|
|
||||||
▲
|
|
||||||
│ extends
|
|
||||||
┌──────────┴──────────┐
|
|
||||||
│ ConcreteClassA/B… │
|
|
||||||
```
|
|
||||||
|
|
||||||
#### Demo:弹窗加载流程(Java)
|
|
||||||
|
|
||||||
```java
|
|
||||||
// 1. 抽象模板
|
|
||||||
public abstract class AbstractDialog {
|
|
||||||
|
|
||||||
// 模板方法:固定调用顺序,设为 final 防止子类改流程
|
|
||||||
public final void show() {
|
|
||||||
initLayout();
|
|
||||||
bindEvent();
|
|
||||||
beforeDisplay(); // 钩子,可选
|
|
||||||
display();
|
|
||||||
afterDisplay(); // 钩子,可选
|
|
||||||
}
|
|
||||||
|
|
||||||
// 具体公共步骤
|
|
||||||
private void initLayout() {
|
|
||||||
System.out.println("加载通用布局文件");
|
|
||||||
}
|
|
||||||
|
|
||||||
// 需要子类实现的抽象步骤
|
|
||||||
protected abstract void bindEvent();
|
|
||||||
|
|
||||||
// 钩子方法,默认空实现
|
|
||||||
protected void beforeDisplay() {}
|
|
||||||
protected void afterDisplay() {}
|
|
||||||
|
|
||||||
private void display() {
|
|
||||||
System.out.println("弹出对话框");
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
// 2. 子类:登录对话框
|
|
||||||
public class LoginDialog extends AbstractDialog {
|
|
||||||
@Override
|
|
||||||
protected void bindEvent() {
|
|
||||||
System.out.println("绑定登录按钮事件");
|
|
||||||
}
|
|
||||||
@Override
|
|
||||||
protected void afterDisplay() {
|
|
||||||
System.out.println("focus 到用户名输入框");
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
// 3. 调用
|
|
||||||
public class Demo {
|
|
||||||
public static void main(String[] args) {
|
|
||||||
AbstractDialog dialog = new LoginDialog();
|
|
||||||
dialog.show();
|
|
||||||
/* 输出:
|
|
||||||
加载通用布局文件
|
|
||||||
绑定登录按钮事件
|
|
||||||
弹出对话框
|
|
||||||
focus 到用户名输入框
|
|
||||||
*/
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**要点**
|
|
||||||
|
|
||||||
- **复用公共流程**:`initLayout()`、`display()` 写一次即可。
|
|
||||||
- **限制流程顺序**:`show()` 定为 `final`,防止子类乱改步骤。
|
|
||||||
- **钩子方法**:子类可选择性覆盖(如 `beforeDisplay`)。
|
|
||||||
|
|
||||||
------
|
|
||||||
|
|
||||||
### 关键区别 & 组合用法
|
|
||||||
|
|
||||||
| | **策略模式** | **模板方法模式** |
|
|
||||||
| ---------------- | ---------------------------------- | ---------------------------------------- |
|
|
||||||
| **目的** | **横向**扩展——允许算法**并列互换** | **纵向**复用——抽取算法**骨架**,固定顺序 |
|
|
||||||
| **实现方式** | 组合 + 接口 | 继承 + 抽象父类 |
|
|
||||||
| **行为选择时机** | 运行时由外部注入 | 编译期由继承确定 |
|
|
||||||
| **常组合** | 与 **工厂模式**配合选择策略 | 与 **钩子方法**、**回调**一起用 |
|
|
||||||
|
|
||||||
在实际项目中,两者经常**组合**:
|
|
||||||
|
|
||||||
> 折扣计算 **Strategy** → 公共过滤 & 日志 **Template Method** → Spring 容器负责策略注册/发现。
|
|
||||||
|
|
||||||
这样即可同时获得“纵向流程复用”+“横向算法可插拔”的双重优势。
|
|
||||||
|
|||||||
Loading…
x
Reference in New Issue
Block a user