Commit on 2025/03/30 周日 20:47:00.18
This commit is contained in:
parent
75d8cb67a1
commit
527903143c
@ -1,10 +1,41 @@
|
||||
# 交替方向乘子法(ADMM)
|
||||
## 凸优化
|
||||
|
||||
### 核心概念
|
||||
|
||||
1. **凸函数**
|
||||
定义:$f(x)$ 是凸函数当且仅当
|
||||
$$
|
||||
f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2), \quad \forall x_1,x_2 \in \text{dom}(f), \theta \in [0,1]
|
||||
$$
|
||||
|
||||
- 示例:$f(x)=x^2$, $f(x)=e^x$
|
||||
|
||||
2. **凸集**
|
||||
定义:集合$X$是凸集当且仅当
|
||||
$$
|
||||
\forall x_1,x_2 \in X, \theta \in [0,1] \Rightarrow \theta x_1 + (1-\theta)x_2 \in X
|
||||
$$
|
||||
|
||||
- 示例:超平面、球体
|
||||
|
||||
### 凸优化问题标准形式
|
||||
|
||||
$$
|
||||
\min_x f(x) \quad \text{s.t.} \quad
|
||||
\begin{cases}
|
||||
g_i(x) \leq 0 & (凸不等式约束) \\
|
||||
h_j(x) = 0 & (线性等式约束) \\
|
||||
x \in X & (凸集约束)
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
## 交替方向乘子法(ADMM)
|
||||
|
||||
**Alternating Direction Method of Multipliers (ADMM)** 是一种用于求解大规模优化问题的高效算法,结合了拉格朗日乘子法和分裂方法的优点。
|
||||
|
||||
---
|
||||
|
||||
## 基本概念
|
||||
### 基本概念
|
||||
|
||||
- **优化问题分解**
|
||||
ADMM 的核心思想是将复杂优化问题分解为多个较简单的子问题,通过引入辅助变量将原问题转化为约束优化问题,使子问题独立求解。
|
||||
@ -17,7 +48,7 @@
|
||||
|
||||
---
|
||||
|
||||
## 算法流程
|
||||
### 算法流程
|
||||
|
||||
1. **问题分解**
|
||||
将原问题分解为两个子问题。假设原问题表示为:
|
||||
@ -40,7 +71,7 @@
|
||||
|
||||
|
||||
|
||||
## 例子
|
||||
### 例子
|
||||
|
||||
下面给出一个简单的数值例子,展示 ADMM 在求解分解问题时的迭代过程。我们构造如下问题:
|
||||
|
||||
@ -95,6 +126,10 @@ $$
|
||||
|
||||
针对本问题可以推导出三个更新步骤:
|
||||
|
||||
$\arg\min_x\; $表示在变量 $x$ 的可行范围内,找到使目标函数 $f(x)$ 最小的 $x$ 的具体值。
|
||||
|
||||
$k$ 代表当前的迭代次数
|
||||
|
||||
1. **更新 $x$:**
|
||||
|
||||
固定 $z$ 和 $y$,求解
|
||||
@ -213,7 +248,7 @@ $$
|
||||
|
||||
|
||||
|
||||
## 应用领域
|
||||
### 应用领域
|
||||
|
||||
- **大规模优化**
|
||||
在大数据、机器学习中利用并行计算加速求解。
|
||||
@ -224,7 +259,7 @@ $$
|
||||
|
||||
---
|
||||
|
||||
## 优点与局限性
|
||||
### 优点与局限性
|
||||
|
||||
| **优点** | **局限性** |
|
||||
| ------------------ | ---------------------- |
|
||||
@ -232,3 +267,156 @@ $$
|
||||
| 支持稀疏性和正则化 | 参数 $\rho$ 需精细调节 |
|
||||
| 收敛性稳定 | — |
|
||||
|
||||
|
||||
|
||||
## KKT 条件
|
||||
|
||||
KKT 条件是用于求解约束优化问题的一组必要条件,特别适用于非线性规划问题。当目标函数是非线性的,并且存在约束时,**KKT 条件提供了优化问题的最优解的必要条件**。
|
||||
|
||||
### 一般形式
|
||||
|
||||
考虑优化问题:
|
||||
$$
|
||||
\min_x f(x)
|
||||
$$
|
||||
约束条件:
|
||||
$$
|
||||
g_i(x) \leq 0, \quad i = 1, 2, \dots, m
|
||||
$$
|
||||
|
||||
$$
|
||||
h_j(x) = 0, \quad j = 1, 2, \dots, p
|
||||
$$
|
||||
|
||||
### KKT 条件
|
||||
|
||||
**1. 拉格朗日函数**
|
||||
|
||||
构造拉格朗日函数:
|
||||
$$
|
||||
\mathcal{L}(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^p \mu_j h_j(x)
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $\lambda_i$ 是不等式约束的拉格朗日乘子
|
||||
- $\mu_j$ 是等式约束的拉格朗日乘子
|
||||
|
||||
**2. 梯度条件(驻点条件)**
|
||||
$$
|
||||
\nabla_x \mathcal{L}(x, \lambda, \mu) = 0
|
||||
$$
|
||||
即:
|
||||
$$
|
||||
\nabla f(x) + \sum_{i=1}^m \lambda_i \nabla g_i(x) + \sum_{j=1}^p \mu_j \nabla h_j(x) = 0
|
||||
$$
|
||||
|
||||
**3. 原始可行性条件**
|
||||
$$
|
||||
g_i(x) \leq 0, \quad i = 1, 2, \dots, m
|
||||
$$
|
||||
|
||||
$$
|
||||
h_j(x) = 0, \quad j = 1, 2, \dots, p
|
||||
$$
|
||||
|
||||
**4. 对偶可行性条件**
|
||||
$$
|
||||
\lambda_i \geq 0, \quad i = 1, 2, \dots, m
|
||||
$$
|
||||
|
||||
**5. 互补松弛性条件**
|
||||
$$
|
||||
\lambda_i g_i(x) = 0, \quad i = 1, 2, \dots, m
|
||||
$$
|
||||
(即:$\lambda_i > 0 \Rightarrow g_i(x) = 0$,或 $g_i(x) < 0 \Rightarrow \lambda_i = 0$)
|
||||
|
||||
|
||||
|
||||
### 示例:
|
||||
|
||||
我们有以下优化问题:
|
||||
$$
|
||||
\min_x \quad f(x) = x^2 \\
|
||||
\text{s.t.} \quad g(x) = x - 1 \leq 0
|
||||
$$
|
||||
|
||||
首先,我们可以直观地理解这个问题:
|
||||
|
||||
- 目标函数f(x)=x²是一个开口向上的抛物线,无约束时最小值在x=0
|
||||
- 约束条件x-1≤0意味着x≤1
|
||||
- 所以我们需要在x≤1的范围内找f(x)的最小值
|
||||
|
||||
显然,无约束最小值x=0已经满足x≤1的约束,因此x=0就是最优解。但让我们看看KKT条件如何形式化地得出这个结论。
|
||||
|
||||
**1. 构造拉格朗日函数**
|
||||
|
||||
拉格朗日函数为:
|
||||
$$
|
||||
\mathcal{L}(x, \lambda) = x^2 + \lambda(x-1), \quad \lambda \geq 0
|
||||
$$
|
||||
|
||||
这里λ是拉格朗日乘子,必须非负(因为是不等式约束)。
|
||||
|
||||
**2. KKT条件**
|
||||
|
||||
KKT条件包括:
|
||||
|
||||
1. 平稳性条件:∇ₓℒ = 0
|
||||
2. 原始可行性:g(x) ≤ 0
|
||||
3. 对偶可行性:λ ≥ 0
|
||||
4. 互补松弛性:λ·g(x) = 0
|
||||
|
||||
**平稳性条件**
|
||||
|
||||
对x求导:
|
||||
$$
|
||||
\frac{\partial \mathcal{L}}{\partial x} = 2x + \lambda = 0 \quad (1)
|
||||
$$
|
||||
|
||||
**互补松弛性**
|
||||
$$
|
||||
\lambda(x-1) = 0 \quad (2)
|
||||
$$
|
||||
|
||||
这意味着有两种情况:
|
||||
|
||||
- 情况1:λ=0
|
||||
- 情况2:x-1=0(即x=1)
|
||||
|
||||
##### 情况1:λ=0
|
||||
|
||||
代入方程(1):
|
||||
2x + 0 = 0 ⇒ x=0
|
||||
|
||||
检查原始可行性:
|
||||
g(0)=0-1=-1≤0 ✔
|
||||
|
||||
检查对偶可行性:
|
||||
λ=0≥0 ✔
|
||||
|
||||
互补松弛性:
|
||||
0·(-1)=0 ✔
|
||||
|
||||
所以x=0, λ=0是一个可能的解。
|
||||
|
||||
##### 情况2:x=1
|
||||
|
||||
代入方程(1):
|
||||
2·1 + λ = 0 ⇒ λ=-2
|
||||
|
||||
检查对偶可行性:
|
||||
λ=-2≥0 ✖ 不满足
|
||||
|
||||
因此这种情况被排除。
|
||||
|
||||
**唯一满足所有KKT条件的解是x=0, λ=0。**
|
||||
|
||||
|
||||
|
||||
### 总结
|
||||
|
||||
KKT 条件通过拉格朗日乘子法将约束和目标函数结合,为求解约束优化问题提供了必要的最优性条件。其核心是:
|
||||
|
||||
1. 拉格朗日函数的梯度为零
|
||||
2. 原始约束和对偶约束的可行性
|
||||
3. 互补松弛性
|
||||
@ -21,7 +21,7 @@
|
||||
|
||||
**状态转移模型**
|
||||
|
||||
设系统的状态向量为 $\mathbf{x}_k$,控制输入为 $\mathbf{u}_k$,过程噪声为 $\mathbf{w}_k$(假设均值为0,协方差矩阵为 $\mathbf{Q}$),状态转移模型可写为:
|
||||
设系统的状态向量为 $\mathbf{x}_k$,控制输入为 $\mathbf{u}_k$,过程噪声为 $\mathbf{w}_k$(假设均值为0,协方差矩阵为 $\mathbf{Q}$,维度和状态向量一致),状态转移模型可写为:
|
||||
|
||||
$$
|
||||
\mathbf{x}_k = \mathbf{A} \mathbf{x}_{k-1} + \mathbf{B} \mathbf{u}_{k-1} + \mathbf{w}_{k-1}
|
||||
@ -250,5 +250,3 @@ H = \begin{bmatrix}
|
||||
0 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
###
|
||||
|
||||
222
科研/数学基础.md
222
科研/数学基础.md
@ -396,16 +396,45 @@ $$
|
||||
|
||||
|
||||
|
||||
## 方差等
|
||||
## 期望、方差、协方差
|
||||
|
||||
### 期望
|
||||
|
||||
$$
|
||||
E(X) = \sum_{i} x_i \cdot P(x_i)
|
||||
$$
|
||||
|
||||
其中: $x_i$ 是随机变量$X$ 的取值, $P(x_i)$ 是 $x_i$ 发生的概率。
|
||||
|
||||
**性质**
|
||||
|
||||
1. **线性性**:
|
||||
$$
|
||||
E(aX + bY) = aE(X) + bE(Y)
|
||||
$$
|
||||
|
||||
2. **独立变量**:
|
||||
$$
|
||||
E(XY) = E(X)E(Y) \quad (\text{当}X,Y\text{独立时})
|
||||
$$
|
||||
|
||||
3. **常数处理**:
|
||||
$$
|
||||
E(c) = c
|
||||
$$
|
||||
|
||||
|
||||
|
||||
### 方差
|
||||
|
||||
**标准差**
|
||||
$$
|
||||
\sigma =\sqrt{\frac{\textstyle\sum_{i=1}^{n}{({x}_{i}-\overline{x})}^{2}}{n}}
|
||||
$$
|
||||
|
||||
**方差**
|
||||
|
||||
它是一个**标量**,表示一个单一随机变量的变动程度。
|
||||
$$
|
||||
Var(X)=\mathrm{E}[{(X-\mu) }^{2}]= {\sigma}^{2}
|
||||
$$
|
||||
@ -415,54 +444,185 @@ $$
|
||||
Var(X)=\mathrm{E}({X}^{2})-{[\mathrm{E}(X)]}^{2} \\
|
||||
Var(kX)={k}^{2}Var(X)
|
||||
$$
|
||||

|
||||
|
||||
|
||||
|
||||
若X和Y是独立的随机变量
|
||||
$$
|
||||
Var(X+Y)=Var(X)+Var(Y)
|
||||
$$
|
||||
|
||||
**协方差**
|
||||
### **协方差**
|
||||
|
||||
给定两个随机变量 $X$ 和 $Y$,其协方差计算公式为:
|
||||
$$
|
||||
\text{Cov}(X,Y) = \sum_{i=1}^n (x_i - \mu_X)(y_i - \mu_Y)
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $x_i, y_i$ 为观测值
|
||||
- $\mu_X, \mu_Y$ 分别为 $X$ 和 $Y$ 的样本均值
|
||||
|
||||
|
||||
|
||||
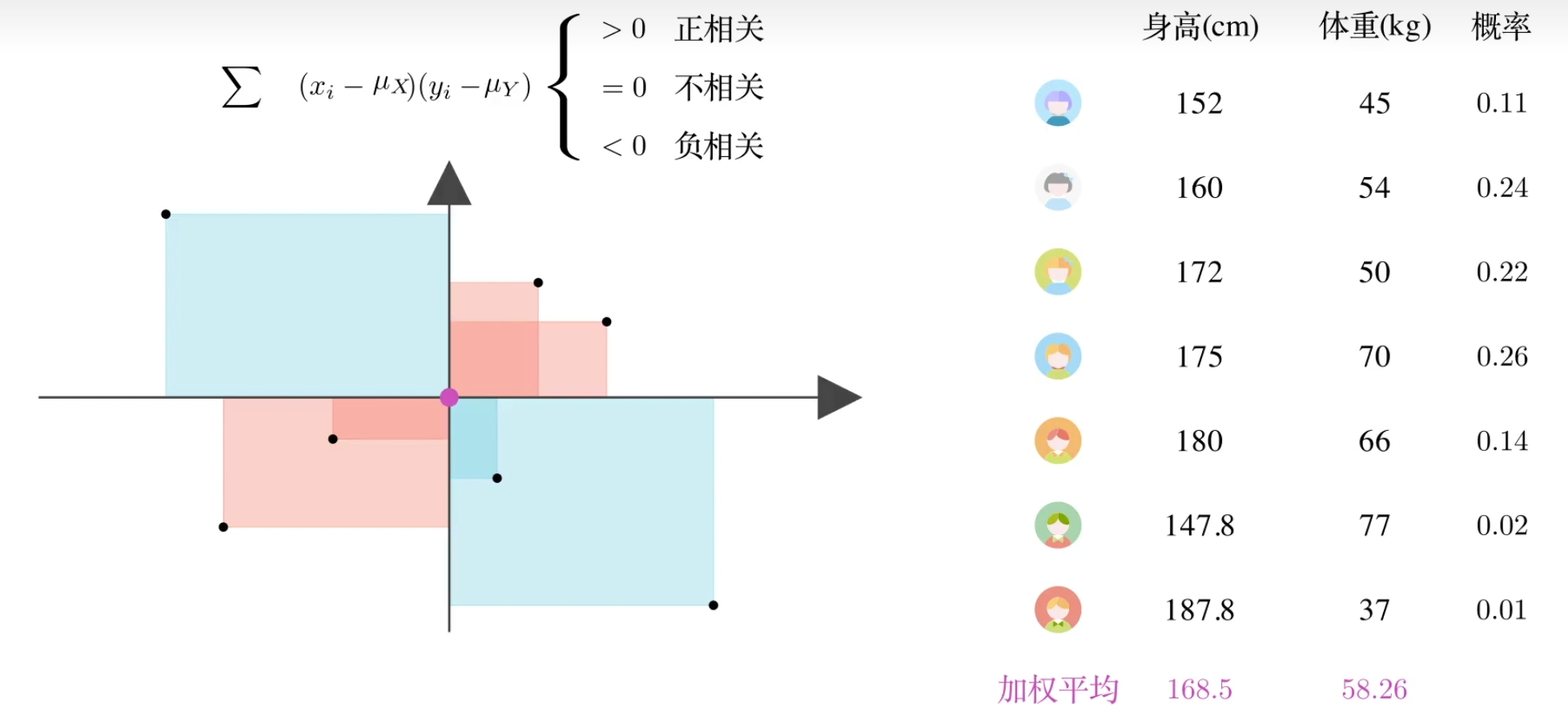
直观理解:如果有$X$,$Y$两个变量,$X$增大,$Y$也**倾向**于增大,$Cov(X,Y)>0$,正相关;$X$增加,$Y$倾向于减小->负相关;否则不相关。
|
||||
|
||||
|
||||
|
||||
推广:概率分布中的协方差
|
||||
|
||||
$\text{Cov}(X,Y) =\sum_{i=1}^n {p}_{i}({x}_{i}-{\mu }_{\mathrm{X}})({\mathcal{y}}_{i}-{\mu }_{Y})=E\left[(X-\mu_X)(Y-\mu_Y)\right]$
|
||||
|
||||
|
||||
|
||||
**性质**
|
||||
|
||||
1. 对称性
|
||||
|
||||
$$
|
||||
\sum {p}_{i}({x}_{i}-{\mu }_{\mathrm{X}})({\mathcal{y}}_{i}-{\mu }_{Y})
|
||||
\\ Cov\begin{pmatrix}X,Y
|
||||
|
||||
\end{pmatrix}=\mathrm{E}\begin{bmatrix}\begin{pmatrix}\mathrm{X}-{\mu }_{\mathrm{X}}
|
||||
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}Y-{\mu }_{Y}
|
||||
|
||||
\end{pmatrix}
|
||||
\end{bmatrix}\\
|
||||
Cov(X,Y)=E(XY)-E(X)E(Y)
|
||||
\text{Cov}(X, Y) = \text{Cov}(Y, X)
|
||||
$$
|
||||
|
||||
**性质:**
|
||||
- 协方差的计算与变量顺序无关
|
||||
|
||||
**X Y表示随机变量**
|
||||
2. 线性性
|
||||
|
||||

|
||||
|
||||
**协方差矩阵**
|
||||
|
||||
协方差矩阵计算了不同维度之间的协方差,它是一个对称矩阵
|
||||
|
||||

|
||||
|
||||
**性质:**
|
||||
|
||||
A为n阶矩阵,X为n维随机向量
|
||||
$$
|
||||
\text{cov}(AX, AX) = A\text{cov}(X, X)A^T
|
||||
\text{Cov}(aX + b, cY + d) = ac \cdot \text{Cov}(X, Y)
|
||||
$$
|
||||
|
||||
3. 零自协方差
|
||||
|
||||
$$
|
||||
\text{Cov}(X, X) = \text{Var}(X)
|
||||
$$
|
||||
|
||||
4. 分解性
|
||||
|
||||
$$
|
||||
\text{Cov}(X_1 + X_2, Y) = \text{Cov}(X_1, Y) + \text{Cov}(X_2, Y)
|
||||
$$
|
||||
|
||||
5. 标量倍数
|
||||
|
||||
$$
|
||||
\text{Cov}(aX, bY) = ab \cdot \text{Cov}(X, Y)
|
||||
$$
|
||||
|
||||
|
||||
|
||||
### **协方差矩阵**
|
||||
|
||||
对于一个随机向量 $\mathbf{X} = [X_1, X_2, \dots, X_n]^T$,其中 $X_1, X_2, \dots, X_n$ 是 $n$ 个随机变量,协方差矩阵 $\Sigma$ 是一个 $n \times n$ 的矩阵,其**元素**表示不同随机变量之间的**协方差**。
|
||||
|
||||
协方差矩阵的元素是通过计算每对随机变量之间的协方差来获得的。协方差矩阵 $\Sigma$ 的元素可以表示为:
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) & \dots & \text{Cov}(X_1, X_n) \\
|
||||
\text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2) & \dots & \text{Cov}(X_2, X_n) \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
\text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \dots & \text{Cov}(X_n, X_n) \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
- 对角线上的元素 $\text{Cov}(X_i, X_i)$ 是每个变量的方差,即 $\text{Var}(X_i)$,
|
||||
- 非对角线上的元素 $\text{Cov}(X_i, X_j)$ 是变量 $X_i$ 和 $X_j$ 之间的协方差。
|
||||
|
||||
|
||||
|
||||
**举例**
|
||||
|
||||
假设我们有两个随机变量 $X$ 和 $Y$,它们的样本数据如下:
|
||||
|
||||
- $X = [4, 7, 8, 5, 6]$
|
||||
- $Y = [2, 3, 6, 7, 4]$
|
||||
|
||||
我们首先计算每个变量的均值、方差和协方差,然后将这些信息组织成协方差矩阵。
|
||||
|
||||
步骤1:计算均值
|
||||
|
||||
- $\mu_X = \frac{4 + 7 + 8 + 5 + 6}{5} = 6$
|
||||
- $\mu_Y = \frac{2 + 3 + 6 + 7 + 4}{5} = 4.4$
|
||||
|
||||
步骤2:计算方差
|
||||
|
||||
- $\text{Var}(X) = \frac{1}{5} \left[(4-6)^2 + (7-6)^2 + (8-6)^2 + (5-6)^2 + (6-6)^2\right] = 2$
|
||||
- $\text{Var}(Y) = \frac{1}{5} \left[(2-4.4)^2 + (3-4.4)^2 + (6-4.4)^2 + (7-4.4)^2 + (4-4.4)^2\right] = 2.64$
|
||||
|
||||
步骤3:计算协方差
|
||||
$$
|
||||
\text{Cov}(X, Y) = \frac{1}{5} \left[(4-6)(2-4.4) + (7-6)(3-4.4) + (8-6)(6-4.4) + (5-6)(7-4.4) + (6-6)(4-4.4)\right]= 4
|
||||
$$
|
||||
|
||||
步骤4:构建协方差矩阵
|
||||
|
||||
根据以上结果,协方差矩阵 $\Sigma$ 是:
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X) & \text{Cov}(X, Y) \\
|
||||
\text{Cov}(X, Y) & \text{Var}(Y)
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
2 & 4 \\
|
||||
4 & 2.64
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
**如何生成均值为0,协方差为Q的噪声?**
|
||||
|
||||
1. 生成标准正态随机变量
|
||||
$$
|
||||
\mathbf{Z} \sim \mathcal{N}(0, \mathbf{I})
|
||||
$$
|
||||
|
||||
2. 进行线性变换
|
||||
$$
|
||||
\mathbf{w}_k = \sqrt{\mathbf{Q}} \cdot \mathbf{Z}
|
||||
$$
|
||||
其中 $\sqrt{\mathbf{Q}}$ 是 $\mathbf{Q}$ 的矩阵平方根。
|
||||
|
||||
3. 验证其协方差确实为Q:
|
||||
$$
|
||||
\begin{aligned}
|
||||
\text{Cov}(\mathbf{w}_k) &= \mathbb{E}[\mathbf{w}_k\mathbf{w}_k^T] \\
|
||||
&= \sqrt{\mathbf{Q}} \cdot \mathbb{E}[\mathbf{Z}\mathbf{Z}^T] \cdot \sqrt{\mathbf{Q}}^T \\
|
||||
&= \sqrt{\mathbf{Q}} \cdot \mathbf{I} \cdot \sqrt{\mathbf{Q}}^T \\
|
||||
&= \mathbf{Q}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
**Python代码示例**
|
||||
|
||||
```python
|
||||
import numpy as np
|
||||
|
||||
# 定义协方差矩阵
|
||||
Q = np.array([[0.1, 0.05],
|
||||
[0.05, 0.2]])
|
||||
|
||||
# Cholesky分解
|
||||
L = np.linalg.cholesky(Q) # L @ L.T = Q
|
||||
|
||||
# 生成标准正态随机数
|
||||
Z = np.random.randn(2)
|
||||
|
||||
# 生成目标噪声
|
||||
w = L @ Z # 等价于 np.dot(L, Z)
|
||||
```
|
||||
|
||||
|
||||
|
||||
$\text{cov}(AX, AX) = A\text{cov}(X, X)A^T$
|
||||
|
||||
**推导:**
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
## 高斯分布
|
||||
|
||||
高斯分布的概率密度函数:
|
||||
|
||||
15
科研/线性代数.md
15
科研/线性代数.md
@ -161,6 +161,21 @@ $$
|
||||
|
||||
|
||||
|
||||
### 基变换
|
||||
|
||||
新基下的变换矩阵 $A_C$ 为:
|
||||
$$
|
||||
A_C = P^{-1} A P
|
||||
$$
|
||||
|
||||
$P$:从原基到新基的**基变换矩阵**(可逆),$P$的每一列代表了新基中的一个基向量
|
||||
|
||||
$A$:线性变换 $T$ 在**原基**下的矩阵表示
|
||||
|
||||
原来空间中进行$A$线性变换等同于新基的视角下进行 $A_C$ 变换
|
||||
|
||||
|
||||
|
||||
### 点积、哈达马积
|
||||
|
||||
**向量点积(Dot Product)**
|
||||
|
||||
90
科研/草稿.md
90
科研/草稿.md
@ -1,41 +1,81 @@
|
||||
# B样条拟合示例:用正弦函数采样作为系数
|
||||
### 协方差矩阵(Covariance Matrix)
|
||||
|
||||
我选择的系数是通过在四个节点处对函数 $f(t) = \sin\left(\dfrac{\pi t}{4}\right)$ 进行采样得到的,对应的是四个基函数 $B_0(t), B_1(t), B_2(t), B_3(t)$,其"峰值"分别位于:
|
||||
**协方差矩阵** 是一个方阵,用来描述一组随机变量之间的协方差关系。它是多元统计分析中的重要工具,尤其在处理多维数据时,协方差矩阵提供了所有变量之间的协方差信息。
|
||||
|
||||
- $B_0(t)$:在 $t = 0$ 处取值 1
|
||||
- $B_1(t)$:在 $t = 1$ 处取值 1
|
||||
- $B_2(t)$:在 $t = 2$ 处取值 1
|
||||
- $B_3(t)$:在 $t = 3$ 处取值 1
|
||||
对于一个随机向量 $\mathbf{X} = [X_1, X_2, \dots, X_n]^T$,其中 $X_1, X_2, \dots, X_n$ 是 $n$ 个随机变量,协方差矩阵 $\Sigma$ 是一个 $n \times n$ 的矩阵,其元素表示不同随机变量之间的协方差。
|
||||
|
||||
## 系数计算过程
|
||||
### 协方差矩阵的定义
|
||||
|
||||
用来拟合的四个系数是函数在基函数峰值位置的采样值:
|
||||
协方差矩阵的元素是通过计算每对随机变量之间的协方差来获得的。协方差矩阵 $\Sigma$ 的元素可以表示为:
|
||||
|
||||
$$
|
||||
\begin{align*}
|
||||
c_0 &= f(0) = \sin(0) = 0 \\
|
||||
c_1 &= f(1) = \sin\left(\frac{\pi}{4}\right) \approx 0.7071 \\
|
||||
c_2 &= f(2) = \sin\left(\frac{\pi}{2}\right) = 1 \\
|
||||
c_3 &= f(3) = \sin\left(\frac{3\pi}{4}\right) \approx 0.7071 \\
|
||||
\end{align*}
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) & \dots & \text{Cov}(X_1, X_n) \\
|
||||
\text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2) & \dots & \text{Cov}(X_2, X_n) \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
\text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \dots & \text{Cov}(X_n, X_n) \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
## 拟合曲线构造
|
||||
其中:
|
||||
|
||||
最终的B样条拟合曲线是基函数的线性组合:
|
||||
- 对角线上的元素 $\text{Cov}(X_i, X_i)$ 是每个变量的方差,即 $\text{Var}(X_i)$,
|
||||
- 非对角线上的元素 $\text{Cov}(X_i, X_j)$ 是变量 $X_i$ 和 $X_j$ 之间的协方差。
|
||||
|
||||
### 协方差矩阵和协方差的关系
|
||||
|
||||
协方差矩阵是多维协方差的扩展。对于一个二维随机变量 $\mathbf{X} = [X_1, X_2]^T$,它的协方差矩阵就是一个 $2 \times 2$ 的矩阵:
|
||||
|
||||
$$
|
||||
S(t) = 0 \cdot B_0(t) + 0.7071 \cdot B_1(t) + 1 \cdot B_2(t) + 0.7071 \cdot B_3(t)
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X_1) & \text{Cov}(X_1, X_2) \\
|
||||
\text{Cov}(X_1, X_2) & \text{Var}(X_2)
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
## 可视化建议
|
||||
所以,协方差矩阵包含了每一对变量之间的协方差信息。如果你有多个随机变量,协方差矩阵将为你提供这些变量之间的所有协方差。
|
||||
|
||||
需要展示以下内容吗?
|
||||
1. 原始函数 $f(t) = \sin(\pi t/4)$ 的曲线
|
||||
2. 四个采样点 $(0,0)$, $(1,0.7071)$, $(2,1)$, $(3,0.7071)$
|
||||
3. 每个基函数 $B_i(t)$ 及其对应的系数 $c_i$
|
||||
4. 最终合成的紫色B样条曲线 $S(t)$
|
||||
### 举个例子
|
||||
|
||||
---
|
||||
假设我们有两个随机变量 $X$ 和 $Y$,它们的样本数据如下:
|
||||
|
||||
这种构造方式展示了B样条的一个重要特性:**系数直接对应曲线在基函数峰值位置的值**(当基函数是标准归一化时)。
|
||||
- $X = [4, 7, 8, 5, 6]$
|
||||
- $Y = [2, 3, 6, 7, 4]$
|
||||
|
||||
我们首先计算每个变量的均值、方差和协方差,然后将这些信息组织成协方差矩阵。
|
||||
|
||||
步骤1:计算均值
|
||||
|
||||
- $\mu_X = \frac{4 + 7 + 8 + 5 + 6}{5} = 6$
|
||||
- $\mu_Y = \frac{2 + 3 + 6 + 7 + 4}{5} = 4.4$
|
||||
|
||||
步骤2:计算方差
|
||||
|
||||
- $\text{Var}(X) = \frac{1}{5} \left[(4-6)^2 + (7-6)^2 + (8-6)^2 + (5-6)^2 + (6-6)^2\right] = 2$
|
||||
- $\text{Var}(Y) = \frac{1}{5} \left[(2-4.4)^2 + (3-4.4)^2 + (6-4.4)^2 + (7-4.4)^2 + (4-4.4)^2\right] = 2.64$
|
||||
|
||||
步骤3:计算协方差
|
||||
$$
|
||||
\text{Cov}(X, Y) = \frac{1}{5} \left[(4-6)(2-4.4) + (7-6)(3-4.4) + (8-6)(6-4.4) + (5-6)(7-4.4) + (6-6)(4-4.4)\right]
|
||||
$$
|
||||
|
||||
我们已经在前面计算过,协方差 $\text{Cov}(X, Y) = 4$。
|
||||
|
||||
步骤4:构建协方差矩阵
|
||||
|
||||
根据以上结果,协方差矩阵 $\Sigma$ 是:
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X) & \text{Cov}(X, Y) \\
|
||||
\text{Cov}(X, Y) & \text{Var}(Y)
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
2 & 4 \\
|
||||
4 & 2.64
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
### 总结
|
||||
|
||||
协方差矩阵是用于描述多个随机变量之间协方差关系的矩阵,它是协方差的自然扩展。当你有多个变量时,协方差矩阵包含了所有变量之间的协方差及每个变量的方差信息。在二维情况中,协方差矩阵是一个 $2 \times 2$ 矩阵,在多维情况下,它是一个 $n \times n$ 矩阵,其中 $n$ 是变量的个数。
|
||||
|
||||
@ -1226,29 +1226,28 @@ public class SpringbootWebConfig2Application {
|
||||
|
||||
5. 控制反转与依赖注入:
|
||||
|
||||
`@Component` ,`@Service`, `@Repository`控制反转
|
||||
`@Component`、`@Service`、`@Repository` 用于标识 bean 并让容器管理它们,从而实现 IoC。
|
||||
|
||||
`@Autowired`,`@Configuration` ,`@Bean`依赖注入
|
||||
`@Autowired`、`@Configuration`、`@Bean` 用于实现 DI,通过容器自动装配或配置 bean 的依赖。
|
||||
|
||||
6. **数据库相关。**@Mapper注解:表示是mybatis中的Mapper接口
|
||||
7. **数据库相关。**
|
||||
`@Mapper`注解:表示是mybatis中的Mapper接口,程序运行时,框架会自动生成接口的实现类对象(代理对象),**并交给Spring的IOC容器管理**
|
||||
|
||||
程序运行时:框架会自动生成接口的实现类对象(代理对象),**并交给Spring的IOC容器管理**
|
||||
`@Select`注解:代表的就是select查询,用于书写select查询语句
|
||||
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
|
||||
7. @SpringBootTest:它会启动 Spring 应用程序上下文,并在测试期间模拟运行整个 Spring Boot 应用程序。这意味着你可以在集成测试中使用 Spring 的各种功能,例如**自动装配、依赖注入、配置加载**等。
|
||||
7. `@SpringBootTest`:它会启动 Spring 应用程序上下文,并在测试期间模拟运行整个 Spring Boot 应用程序。这意味着你可以在集成测试中使用 Spring 的各种功能,例如**自动装配、依赖注入、配置加载**等。
|
||||
|
||||
9. lombok的相关注解。非常实用的工具库。
|
||||
|
||||
| **注解** | **作用** |
|
||||
| ------------------- | ------------------------------------------------------------ |
|
||||
| @Getter/@Setter | 为所有的属性提供get/set方法 |
|
||||
| @ToString | 会给类自动生成易阅读的 toString 方法 |
|
||||
| @EqualsAndHashCode | 根据类所拥有的非静态字段自动重写 equals 方法和 hashCode 方法 |
|
||||
| **@Data** | **提供了更综合的生成代码功能(@Getter + @Setter + @ToString + @EqualsAndHashCode)** |
|
||||
| @NoArgsConstructor | 为实体类生成无参的构造器方法 |
|
||||
| @AllArgsConstructor | 为实体类生成除了static修饰的字段之外带有各参数的构造器方法。 |
|
||||
| **@Slf4j** | 可以log.info("输出日志信息"); |
|
||||
| **注解** | **作用** |
|
||||
| ----------------------- | ------------------------------------------------------------ |
|
||||
| @Getter/@Setter | 为所有的属性提供get/set方法 |
|
||||
| @ToString | 会给类自动生成易阅读的 toString 方法 |
|
||||
| @EqualsAndHashCode | 根据类所拥有的非静态字段自动重写 equals 方法和 hashCode 方法 |
|
||||
| **@Data** | **提供了更综合的生成代码功能(@Getter + @Setter + @ToString + @EqualsAndHashCode)** |
|
||||
| **@NoArgsConstructor** | 为实体类生成无参的构造器方法 |
|
||||
| **@AllArgsConstructor** | 为实体类生成除了static修饰的字段之外带有各参数的构造器方法。 |
|
||||
| **@Slf4j** | 可以log.info("输出日志信息"); |
|
||||
|
||||
```java
|
||||
//equals 方法用于比较两个对象的内容是否相同
|
||||
@ -1257,18 +1256,39 @@ public class SpringbootWebConfig2Application {
|
||||
System.out.println(addr1.equals(addr2)); // 输出 true
|
||||
```
|
||||
|
||||
10. @Test,Junit测试单元,可在测试类中定义测试函数,一次性执行所有@Test注解下的函数,不用写main方法
|
||||
10. `@Test`,Junit测试单元,可在测试类中定义测试函数,一次性执行所有@Test注解下的函数,不用写main方法
|
||||
|
||||
11. @Override,当一个方法在子类中覆盖(重写)了父类中的同名方法时,为了确保正确性,可以使用 `@Override` 注解来标记这个方法,这样编译器就能够帮助检查是否正确地重写了父类的方法。
|
||||
11. `@Override`,当一个方法在子类中覆盖(重写)了父类中的同名方法时,为了确保正确性,可以使用 `@Override` 注解来标记这个方法,这样编译器就能够帮助检查是否正确地重写了父类的方法。
|
||||
|
||||
11. @DateTimeFormat(pattern = "yyyy-MM-dd") LocalDate begin,
|
||||
12. `@DateTimeFormat`将日期转化为指定的格式。Spring会尝试将接收到的**字符串参数**转换为控制器方法参数的相应类型。
|
||||
|
||||
将日期转化为指定的格式。Spring会尝试将接收到的**字符串参数**转换为控制器方法参数的相应类型。
|
||||
```java
|
||||
@RestController
|
||||
public class DateController {
|
||||
|
||||
// 例如:请求 URL 为 /search?begin=2025-03-28
|
||||
@GetMapping("/search")
|
||||
public String search(@RequestParam("begin") @DateTimeFormat(pattern = "yyyy-MM-dd") LocalDate begin) {
|
||||
// 此时 begin 已经是 LocalDate 类型,可以直接使用
|
||||
return "接收到的日期是: " + begin;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
12. @RestControllerAdvice= @ControllerAdvice + @ResponseBody。加上这个注解就代表我们定义了一个全局异常处理器,而且处理异常的方法返回值会转换为json后再响应给前端
|
||||
12. @Configuration和@Bean配合使用,可以对第三方bean进行**集中**的配置管理,依赖注入!!@Bean用于方法上
|
||||
|
||||
加了@Configuration,当Spring Boot应用**启动时,它会执行**一系列的自动配置步骤。
|
||||
```java
|
||||
@RestControllerAdvice
|
||||
public class GlobalExceptionHandler {
|
||||
@ExceptionHandler(Exception.class)
|
||||
@ResponseStatus(HttpStatus.INTERNAL_SERVER_ERROR)
|
||||
public String handleException(Exception ex) {
|
||||
// 返回错误提示或错误详情
|
||||
return "系统发生异常:" + ex.getMessage();
|
||||
}
|
||||
}
|
||||
```
|
||||
12. `@Configuration`和`@Bean`配合使用,可以对第三方bean进行**集中**的配置管理,依赖注入!!`@Bean`用于方法上。加了`@Configuration`,当Spring Boot应用**启动时,它会执行**一系列的自动配置步骤。
|
||||
|
||||
12. `@ComponentScan`指定了Spring应该在哪些包下搜索带有`@Component`、`@Service`、`@Repository`、`@Controller`等注解的类,以便将这些类自动注册为Spring容器管理的Bean.`@SpringBootApplication`它是一个便利的注解,组合了`@Configuration`、`@EnableAutoConfiguration`和`@ComponentScan`注解。
|
||||
|
||||
|
||||
@ -2,14 +2,28 @@
|
||||
|
||||
## 安装启动Mysql
|
||||
|
||||
### 启动Mysql
|
||||
**mysql**
|
||||
|
||||
- 是 MySQL 的命令行**客户端**工具,用于连接、查询和管理 MySQL 数据库。
|
||||
- 你可以通过它来执行 SQL 命令、查看数据和管理数据库。
|
||||
|
||||
**mysqld**
|
||||
|
||||
- 是 MySQL 服务器守护进程,也就是 MySQL 数据库的**实际运行**程序。
|
||||
- 它负责处理数据库的存储、查询、并发访问、用户验证等核心任务。
|
||||
|
||||
**添加环境变量:**
|
||||
|
||||
将`'\path\to\mysql-8.0.31-winx64\bin\'`目录添加到 PATH 环境变量中,便于命令行操作。
|
||||
|
||||
**启动Mysql**
|
||||
|
||||
```text
|
||||
net start mysql // 启动mysql服务
|
||||
net stop mysql // 停止mysql服务
|
||||
```
|
||||
|
||||
### 修改root账户密码
|
||||
**修改root账户密码**
|
||||
|
||||
```text
|
||||
mysqladmin -u root password 123456
|
||||
@ -17,7 +31,7 @@ mysqladmin -u root password 123456
|
||||
|
||||
本地windows下的账号:root 密码: 123456
|
||||
|
||||
### 登录
|
||||
**登录**
|
||||
|
||||
```text
|
||||
mysql -u用户名 -p密码 [-h数据库服务器的IP地址 -P端口号]
|
||||
@ -31,15 +45,32 @@ mysql -uroot -p123456
|
||||
|
||||
-P 参数不加,默认连接的端口号是 3306
|
||||
|
||||
**图形化工具**
|
||||
|
||||
推荐Navicat
|
||||
|
||||
|
||||
|
||||
## Mysql简介
|
||||
|
||||
### 通用语法
|
||||
|
||||
1、SQL语句可以单行或多行书写,以分号结尾。
|
||||
1、SQL语句可以单行或多行书写,**以分号结尾**。
|
||||
|
||||
2、SQL语句可以使用空格/缩进来增强语句的可读性。
|
||||
2、SQL语句可以使用空格/缩进来增强语句的可读性。因为SQL语句在执行时,数据库会忽略额外的空格和换行符
|
||||
|
||||
3、MySQL数据库的SQL语句不区分大小写。
|
||||
```mysql
|
||||
SELECT
|
||||
name,
|
||||
age,
|
||||
address
|
||||
FROM
|
||||
users
|
||||
WHERE
|
||||
age > 18;
|
||||
```
|
||||
|
||||
3、MySQL数据库的SQL语句**不区分大小写**。
|
||||
|
||||
4、注释:
|
||||
|
||||
@ -51,25 +82,46 @@ mysql -uroot -p123456
|
||||
| **分类** | **全称** | **说明** |
|
||||
| -------- | --------------------------- | ------------------------------------------------------ |
|
||||
| DDL | Data Definition Language | 数据定义语言,用来定义数据库对象(数据库,表,字段) |
|
||||
| DML | Data Manipulation Language | 数据操作语言,用来对数据库表中的数据进行增删改 |
|
||||
| DQL | Data Query Language | 数据查询语言,用来查询数据库中表的记录 |
|
||||
| **DML** | Data Manipulation Language | 数据操作语言,用来对数据库表中的数据进行**增删改** |
|
||||
| DQL | Data Query Language | 数据查询语言,用来**查询**数据库中表的记录 |
|
||||
| DCL | Data Control Language | 数据控制语言,用来创建数据库用户、控制数据库的访问权限 |
|
||||
|
||||
### 数据类型
|
||||
|
||||
char:声明的字段如果数据类型为char,则该字段占据的长度固定为声明时的值,例如:char(4),存入值 'ab',其长度仍为4.
|
||||
**字符串类型**
|
||||
|
||||
varchar:声明字段时,字段占据的实际长度等于存储内容的实际长度+记录长度的字节(一般是一个字节或者两个字节)例如:varchar(100)表示可以存100,但是存储值'ab'时,占用长度是3字节。
|
||||
CHAR(n):声明的字段如果数据类型为char,则该字段占据的**长度固定**为声明时的值,例如:char(4),存入值 'ab',其长度仍为4.
|
||||
|
||||
日期时间类型:
|
||||
VARCHAR(n):varchar(100)表示最多可以存100个字符,每个字符占用的字节数取决于所使用的字符集。存储开销:除了存储实际数据外,`varchar` 类型还会额外存储 1 或 2 个字节来记录字符串的长度。
|
||||
|
||||
TEXT:用于存储大文本数据,存储长度远大于 VARCHAR,但不支持索引整列内容(通常索引长度有限制)。
|
||||
|
||||
|
||||
|
||||
**日期时间类型:**
|
||||
|
||||
| 类型 | 大小 | 范围 | 格式 | 描述 |
|
||||
| ------------ | ---- | ------------------------------------------ | ------------------- | ---------------- |
|
||||
| DATE | 3 | 1000-01-01 至 9999-12-31 | YYYY-MM-DD | 日期值 |
|
||||
| TIME | 3 | -838:59:59 至 838:59:59 | HH:MM:SS | 时间值或持续时间 |
|
||||
| **DATETIME** | 8 | 1000-01-01 00:00:00 至 9999-12-31 23:59:59 | YYYY-MM-DD HH:MM:SS | 混合日期和时间值 |
|
||||
|
||||
**注意**:字符串和日期时间型数据在 SQL 语句中应包含在引号内,例如:`'2025-03-29'`、`'hello'`。
|
||||
|
||||
|
||||
|
||||
**数值类型**
|
||||
|
||||
| 类型 | 大小 | 有符号(SIGNED)范围 | 无符号(UNSIGNED)范围 | 描述 |
|
||||
| ----------- | ------ | ---------------------------------------- | ------------------------------------------ | ------------------ |
|
||||
| TINYINT | 1byte | (-128,127) | (0,255) | 小整数值 |
|
||||
| INT/INTEGER | 4bytes | (-2^31,2^31-1) | (0,2^32-1) | 大整数值 |
|
||||
| FLOAT | 4bytes | (-3.402823466 E+38,3.402823466351 E+38) | 0 和 (1.175494351 E-38,3.402823466 E+38) | 单精度浮点数值 |
|
||||
| DECIMAL | | 依赖于M(精度)和D(标度)的值 | 依赖于M(精度)和D(标度)的值 | 小数值(精确定点数) |
|
||||
|
||||
**DECIMAL(M, D)**:定点数类型,M 表示总位数,D 表示小数位数,适合存储精度要求较高的数值(如金钱)。
|
||||
|
||||
| 类型 | 大小 | 范围 | 格式 | 描述 |
|
||||
| -------- | ---- | ------------------------------------------ | ------------------- | ---------------- |
|
||||
| DATE | 3 | 1000-01-01 至 9999-12-31 | YYYY-MM-DD | 日期值 |
|
||||
| TIME | 3 | -838:59:59 至 838:59:59 | HH:MM:SS | 时间值或持续时间 |
|
||||
| DATETIME | 8 | 1000-01-01 00:00:00 至 9999-12-31 23:59:59 | YYYY-MM-DD HH:MM:SS | 混合日期和时间值 |
|
||||
|
||||
**字符串和日期型数据都应包含在引号中**
|
||||
|
||||
## DDL
|
||||
|
||||
@ -93,7 +145,7 @@ create database itcast;
|
||||
use itcast;
|
||||
```
|
||||
|
||||
**查询当前使用的数据库:**
|
||||
**查询当前正常使用的数据库:**
|
||||
|
||||
```mysql
|
||||
select database();
|
||||
@ -105,6 +157,8 @@ select database();
|
||||
drop database if exists itcast; -- itcast数据库存在时删除,不存在也不报错
|
||||
~~~
|
||||
|
||||
|
||||
|
||||
### 表操作
|
||||
|
||||
**查询当前数据库下所有表**
|
||||
@ -121,6 +175,15 @@ desc tb_tmps; ( tb_tmps为表名)
|
||||
|
||||
**创建表**
|
||||
|
||||
通常一个列定义的顺序如下:
|
||||
|
||||
1. 列名(字段)
|
||||
2. 字段类型
|
||||
3. 可选的字符集或排序规则(如果需要)
|
||||
4. 约束:例如 `NOT NULL`、`UNIQUE`、`PRIMARY KEY`、`DEFAULT` 等
|
||||
5. 特殊属性:例如 `AUTO_INCREMENT`
|
||||
6. 注释:例如 `COMMENT '说明'`
|
||||
|
||||
```mysql
|
||||
create table 表名(
|
||||
字段1 字段1类型 [约束] [comment 字段1注释 ],
|
||||
|
||||
@ -50,6 +50,26 @@ if (flag == false) { //更常用!
|
||||
|
||||
|
||||
|
||||
#### Character好用的方法
|
||||
|
||||
`Character.isDigit(char c)`用于判断一个字符是否是一个数字字符
|
||||
|
||||
`Character.isLetter(char c)`用于判断字符是否是一个字母(大小写字母都可以)。
|
||||
|
||||
`Character.isLowerCase(char c)`判断字符是否是小写字母。
|
||||
|
||||
`Character.toLowerCase(char c)`将字符转换为小写字母。
|
||||
|
||||
|
||||
|
||||
#### Integer好用的方法
|
||||
|
||||
`Integer.parseInt(String s)`:将字符串 `s` 解析为一个整数(`int`)。
|
||||
|
||||
`Integer.toString(int i)`:将 `int` 转换为字符串。
|
||||
|
||||
|
||||
|
||||
### 常用数据结构
|
||||
|
||||
#### `String`
|
||||
@ -122,13 +142,24 @@ public class StringBufferExample {
|
||||
}
|
||||
```
|
||||
|
||||
StringBuffer有库函数可以翻转,String未提供!
|
||||
`StringBuffer`有库函数可以翻转,String未提供!
|
||||
|
||||
```java
|
||||
StringBuilder sb = new StringBuilder(s);
|
||||
String reversed = sb.reverse().toString();
|
||||
```
|
||||
|
||||
StringBuffer清空内容:
|
||||
|
||||
```java
|
||||
StringBuffer sb = new StringBuffer("Hello, world!");
|
||||
System.out.println("Before clearing: " + sb);
|
||||
// 清空 StringBuffer
|
||||
sb.setLength(0);
|
||||
```
|
||||
|
||||
`StringBuffer` 的 `append()` 方法不仅支持添加普通的字符串,也可以直接将另一个 `StringBuffer` 对象添加到当前的 `StringBuffer`。
|
||||
|
||||
|
||||
|
||||
#### `HashMap`
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user