Commit on 2025/04/02 周三 18:28:46.48
This commit is contained in:
parent
527903143c
commit
5545322a6e
153
科研/数学基础.md
153
科研/数学基础.md
@ -506,11 +506,44 @@ $$
|
||||
\text{Cov}(aX, bY) = ab \cdot \text{Cov}(X, Y)
|
||||
$$
|
||||
|
||||
$\text{cov}(AX, AX) = A\text{cov}(X, X)A^T$
|
||||
|
||||
**推导:**
|
||||
|
||||
(1) 展开协方差定义
|
||||
$$
|
||||
\text{cov}(AX, AX) = \mathbb{E}[(AX - \mathbb{E}[AX])(AX - \mathbb{E}[AX])^T]
|
||||
$$
|
||||
|
||||
(2) 线性期望性质
|
||||
$$
|
||||
\mathbb{E}[AX] = A\mathbb{E}[X] \\
|
||||
\Rightarrow AX - \mathbb{E}[AX] = A(X - \mathbb{E}[X])
|
||||
$$
|
||||
|
||||
(3) 代入展开式
|
||||
$$
|
||||
= \mathbb{E}[A(X - \mathbb{E}[X])(A(X - \mathbb{E}[X]))^T] \\
|
||||
= \mathbb{E}[A(X - \mathbb{E}[X])(X - \mathbb{E}[X])^T A^T]
|
||||
$$
|
||||
|
||||
(4) 提取常数矩阵
|
||||
$$
|
||||
= A \mathbb{E}[(X - \mathbb{E}[X])(X - \mathbb{E}[X])^T] A^T
|
||||
$$
|
||||
|
||||
(5) 协方差矩阵表示
|
||||
$$
|
||||
= A \text{cov}(X, X) A^T
|
||||
$$
|
||||
|
||||
|
||||
|
||||
### **协方差矩阵**
|
||||
|
||||
对于一个随机向量 $\mathbf{X} = [X_1, X_2, \dots, X_n]^T$,其中 $X_1, X_2, \dots, X_n$ 是 $n$ 个随机变量,协方差矩阵 $\Sigma$ 是一个 $n \times n$ 的矩阵,其**元素**表示不同随机变量之间的**协方差**。
|
||||
对于一个随机向量 $\mathbf{X} = [X_1, X_2, \dots, X_n]^T$,其中 $X_1, X_2, \dots, X_n$ 是 $n$ 个随机变量,协方差矩阵 $\Sigma$ 是一个 $n \times n$ 的矩阵,其**元素**表示不同**随机变量**之间的**协方差**。
|
||||
|
||||
(注意:每对变量指的是$\mathbf{X}$中任意两个分量之间的组合,如$X_1, X_2$)
|
||||
|
||||
协方差矩阵的元素是通过计算每对随机变量之间的协方差来获得的。协方差矩阵 $\Sigma$ 的元素可以表示为:
|
||||
|
||||
@ -525,53 +558,90 @@ $$
|
||||
|
||||
其中:
|
||||
|
||||
- 对角线上的元素 $\text{Cov}(X_i, X_i)$ 是每个变量的方差,即 $\text{Var}(X_i)$,
|
||||
- 对角线上的元素 $\text{Cov}(X_i, X_i)$ 是每个变量的方差,即 $\text{Var}(X_i)$。
|
||||
- 非对角线上的元素 $\text{Cov}(X_i, X_j)$ 是变量 $X_i$ 和 $X_j$ 之间的协方差。
|
||||
|
||||
|
||||
|
||||
**举例**
|
||||
**计算举例**
|
||||
|
||||
假设我们有两个随机变量 $X$ 和 $Y$,它们的样本数据如下:
|
||||
|
||||
- $X = [4, 7, 8, 5, 6]$
|
||||
- $Y = [2, 3, 6, 7, 4]$
|
||||
|
||||
我们首先计算每个变量的均值、方差和协方差,然后将这些信息组织成协方差矩阵。
|
||||
|
||||
步骤1:计算均值
|
||||
|
||||
- $\mu_X = \frac{4 + 7 + 8 + 5 + 6}{5} = 6$
|
||||
- $\mu_Y = \frac{2 + 3 + 6 + 7 + 4}{5} = 4.4$
|
||||
|
||||
步骤2:计算方差
|
||||
|
||||
- $\text{Var}(X) = \frac{1}{5} \left[(4-6)^2 + (7-6)^2 + (8-6)^2 + (5-6)^2 + (6-6)^2\right] = 2$
|
||||
- $\text{Var}(Y) = \frac{1}{5} \left[(2-4.4)^2 + (3-4.4)^2 + (6-4.4)^2 + (7-4.4)^2 + (4-4.4)^2\right] = 2.64$
|
||||
|
||||
步骤3:计算协方差
|
||||
$$
|
||||
\text{Cov}(X, Y) = \frac{1}{5} \left[(4-6)(2-4.4) + (7-6)(3-4.4) + (8-6)(6-4.4) + (5-6)(7-4.4) + (6-6)(4-4.4)\right]= 4
|
||||
$$
|
||||
|
||||
步骤4:构建协方差矩阵
|
||||
|
||||
根据以上结果,协方差矩阵 $\Sigma$ 是:
|
||||
假设我们有 **3 个特征**($n=3$)和 **4 个样本**($m=4$),则数据矩阵 $X$ 的构造如下:
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X) & \text{Cov}(X, Y) \\
|
||||
\text{Cov}(X, Y) & \text{Var}(Y)
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
2 & 4 \\
|
||||
4 & 2.64
|
||||
X =
|
||||
\begin{bmatrix}
|
||||
x_1^{(1)} & x_1^{(2)} & x_1^{(3)} & x_1^{(4)} \\
|
||||
x_2^{(1)} & x_2^{(2)} & x_2^{(3)} & x_2^{(4)} \\
|
||||
x_3^{(1)} & x_3^{(2)} & x_3^{(3)} & x_3^{(4)}
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
假设特征为:
|
||||
|
||||
- 第1行 $x_1$:身高(cm)
|
||||
- 第2行 $x_2$:体重(kg)
|
||||
- 第3行 $x_3$:年龄(岁)
|
||||
|
||||
对应4个样本(人)的数据:
|
||||
$$
|
||||
X =
|
||||
\begin{bmatrix}
|
||||
170 & 165 & 180 & 155 \\
|
||||
65 & 55 & 75 & 50 \\
|
||||
30 & 25 & 40 & 20
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
1. **中心化数据**(每行减去均值):
|
||||
|
||||
- 计算每行均值:
|
||||
$$
|
||||
\mu_1 = \frac{170+165+180+155}{4} = 167.5, \quad \mu_2 = 61.25, \quad \mu_3 = 28.75
|
||||
$$
|
||||
|
||||
- 中心化后的矩阵 $X_c$:
|
||||
$$
|
||||
X_c =
|
||||
\begin{bmatrix}
|
||||
2.5 & -2.5 & 12.5 & -12.5 \\
|
||||
3.75 & -6.25 & 13.75 & -11.25 \\
|
||||
1.25 & -3.75 & 11.25 & -8.75
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
2. **计算协方差矩阵**:
|
||||
$$
|
||||
\text{Cov} = \frac{1}{m} X_c X_c^T = \frac{1}{4}
|
||||
\begin{bmatrix}
|
||||
2.5 & -2.5 & 12.5 & -12.5 \\
|
||||
3.75 & -6.25 & 13.75 & -11.25 \\
|
||||
1.25 & -3.75 & 11.25 & -8.75
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
2.5 & 3.75 & 1.25 \\
|
||||
-2.5 & -6.25 & -3.75 \\
|
||||
12.5 & 13.75 & 11.25 \\
|
||||
-12.5 & -11.25 & -8.75
|
||||
\end{bmatrix}
|
||||
$$
|
||||
最终结果(对称矩阵):
|
||||
$$
|
||||
\text{Cov} \approx
|
||||
\begin{bmatrix}
|
||||
93.75 & 100.31 & 62.50 \\
|
||||
100.31 & 120.31 & 75.00 \\
|
||||
62.50 & 75.00 & 48.44
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
- 对角线是各特征的方差(如身高的方差为93.75)
|
||||
- 非对角线是协方差(如身高与体重的协方差为100.31)
|
||||
|
||||
|
||||
**如何生成均值为0,协方差为Q的噪声?**
|
||||
|
||||
|
||||
|
||||
### **如何生成均值为0,协方差为Q的噪声?**
|
||||
|
||||
1. 生成标准正态随机变量
|
||||
$$
|
||||
@ -615,14 +685,6 @@ w = L @ Z # 等价于 np.dot(L, Z)
|
||||
|
||||
|
||||
|
||||
$\text{cov}(AX, AX) = A\text{cov}(X, X)A^T$
|
||||
|
||||
**推导:**
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
## 高斯分布
|
||||
|
||||
高斯分布的概率密度函数:
|
||||
@ -1153,11 +1215,12 @@ $$
|
||||
|
||||
|
||||
|
||||
## **谱分解**
|
||||
## **谱分解**与网络重构
|
||||
|
||||
一个对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的对称矩阵 $A$,其谱分解可以表示为:
|
||||
|
||||
$$
|
||||
A = Q \Lambda Q^T \\
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
|
||||
100
科研/草稿.md
100
科研/草稿.md
@ -1,81 +1,47 @@
|
||||
### 协方差矩阵(Covariance Matrix)
|
||||
- # FCM算法时间复杂度分析
|
||||
|
||||
**协方差矩阵** 是一个方阵,用来描述一组随机变量之间的协方差关系。它是多元统计分析中的重要工具,尤其在处理多维数据时,协方差矩阵提供了所有变量之间的协方差信息。
|
||||
## 1. FCM算法的步骤与时间复杂度
|
||||
|
||||
对于一个随机向量 $\mathbf{X} = [X_1, X_2, \dots, X_n]^T$,其中 $X_1, X_2, \dots, X_n$ 是 $n$ 个随机变量,协方差矩阵 $\Sigma$ 是一个 $n \times n$ 的矩阵,其元素表示不同随机变量之间的协方差。
|
||||
### **1. 初始化步骤**
|
||||
- **初始化簇中心**:需要 $O(K)$ 时间($K$ 是簇数)
|
||||
- **初始化隶属度矩阵 $U$**($n \times K$ 矩阵):$O(nK)$
|
||||
|
||||
### 协方差矩阵的定义
|
||||
### **2. 更新隶属度**
|
||||
- 每个数据点 $a_{ij}$ 计算与每个簇中心 $c_k$ 的距离:$O(K)$
|
||||
- 更新所有数据点的隶属度矩阵:$O(nK^2)$
|
||||
|
||||
协方差矩阵的元素是通过计算每对随机变量之间的协方差来获得的。协方差矩阵 $\Sigma$ 的元素可以表示为:
|
||||
### **3. 更新簇中心**
|
||||
- 计算每个簇的新中心(加权平均):$O(nK)$
|
||||
- 总体簇中心更新:$O(nK)$
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) & \dots & \text{Cov}(X_1, X_n) \\
|
||||
\text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2) & \dots & \text{Cov}(X_2, X_n) \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
\text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \dots & \text{Cov}(X_n, X_n) \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
### **4. 判断收敛**
|
||||
- 计算簇中心变化量 $\Delta C$:$O(K)$
|
||||
|
||||
其中:
|
||||
### **5. 量化处理**
|
||||
- 将元素分配到簇并替换值:$O(nK)$
|
||||
|
||||
- 对角线上的元素 $\text{Cov}(X_i, X_i)$ 是每个变量的方差,即 $\text{Var}(X_i)$,
|
||||
- 非对角线上的元素 $\text{Cov}(X_i, X_j)$ 是变量 $X_i$ 和 $X_j$ 之间的协方差。
|
||||
## 2. 总时间复杂度
|
||||
|
||||
### 协方差矩阵和协方差的关系
|
||||
每次迭代的总时间复杂度:
|
||||
$$
|
||||
O(nK^2) + O(nK) + O(K) \approx O(nK^2)
|
||||
$$
|
||||
|
||||
协方差矩阵是多维协方差的扩展。对于一个二维随机变量 $\mathbf{X} = [X_1, X_2]^T$,它的协方差矩阵就是一个 $2 \times 2$ 的矩阵:
|
||||
其中:
|
||||
- $n$:数据点数量
|
||||
- $K$:簇数量
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X_1) & \text{Cov}(X_1, X_2) \\
|
||||
\text{Cov}(X_1, X_2) & \text{Var}(X_2)
|
||||
\end{bmatrix}
|
||||
$$
|
||||
## 3. 初始簇中心选取优化方法的时间复杂度
|
||||
|
||||
所以,协方差矩阵包含了每一对变量之间的协方差信息。如果你有多个随机变量,协方差矩阵将为你提供这些变量之间的所有协方差。
|
||||
- 选择 $K$ 个簇中心时:
|
||||
- 需要计算候选集内元素间最小距离
|
||||
- 每次选择复杂度:$O(n^2)$
|
||||
- 总体选择复杂度:$O(Kn^2)$
|
||||
|
||||
### 举个例子
|
||||
## 4. 图片分析结论
|
||||
|
||||
假设我们有两个随机变量 $X$ 和 $Y$,它们的样本数据如下:
|
||||
图片中的时间复杂度分析是合理的:
|
||||
- **标准FCM算法**:$O(nK^2)$
|
||||
- **优化簇中心选择**:$O(n^3)$
|
||||
|
||||
- $X = [4, 7, 8, 5, 6]$
|
||||
- $Y = [2, 3, 6, 7, 4]$
|
||||
|
||||
我们首先计算每个变量的均值、方差和协方差,然后将这些信息组织成协方差矩阵。
|
||||
|
||||
步骤1:计算均值
|
||||
|
||||
- $\mu_X = \frac{4 + 7 + 8 + 5 + 6}{5} = 6$
|
||||
- $\mu_Y = \frac{2 + 3 + 6 + 7 + 4}{5} = 4.4$
|
||||
|
||||
步骤2:计算方差
|
||||
|
||||
- $\text{Var}(X) = \frac{1}{5} \left[(4-6)^2 + (7-6)^2 + (8-6)^2 + (5-6)^2 + (6-6)^2\right] = 2$
|
||||
- $\text{Var}(Y) = \frac{1}{5} \left[(2-4.4)^2 + (3-4.4)^2 + (6-4.4)^2 + (7-4.4)^2 + (4-4.4)^2\right] = 2.64$
|
||||
|
||||
步骤3:计算协方差
|
||||
$$
|
||||
\text{Cov}(X, Y) = \frac{1}{5} \left[(4-6)(2-4.4) + (7-6)(3-4.4) + (8-6)(6-4.4) + (5-6)(7-4.4) + (6-6)(4-4.4)\right]
|
||||
$$
|
||||
|
||||
我们已经在前面计算过,协方差 $\text{Cov}(X, Y) = 4$。
|
||||
|
||||
步骤4:构建协方差矩阵
|
||||
|
||||
根据以上结果,协方差矩阵 $\Sigma$ 是:
|
||||
|
||||
$$
|
||||
\Sigma = \begin{bmatrix}
|
||||
\text{Var}(X) & \text{Cov}(X, Y) \\
|
||||
\text{Cov}(X, Y) & \text{Var}(Y)
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
2 & 4 \\
|
||||
4 & 2.64
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
### 总结
|
||||
|
||||
协方差矩阵是用于描述多个随机变量之间协方差关系的矩阵,它是协方差的自然扩展。当你有多个变量时,协方差矩阵包含了所有变量之间的协方差及每个变量的方差信息。在二维情况中,协方差矩阵是一个 $2 \times 2$ 矩阵,在多维情况下,它是一个 $n \times n$ 矩阵,其中 $n$ 是变量的个数。
|
||||
该分析准确反映了FCM算法的计算复杂度。
|
||||
|
||||
117
科研/郭款论文.md
117
科研/郭款论文.md
@ -1,3 +1,5 @@
|
||||
KAN不稳定/卡尔曼滤波 小波变换
|
||||
|
||||
## 郭款论文
|
||||
|
||||
### **整体逻辑**
|
||||
@ -28,12 +30,6 @@
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
# KAN不稳定/卡尔曼滤波 小波变换
|
||||
|
||||
|
||||
|
||||
### 矢量量化
|
||||
|
||||
矢量量化的基本思想是将输入数据点视为多维向量,并将其映射到一个码本(codebook)中的最接近的码字。码本是预先确定的一组离散的向量,通常通过无监督学习方法(如**K-means**)从大量训练数据中得到。在矢量量化中,输入数据点与码本中的码字之间的距离度量通常使用**欧氏距离**。通过选择最接近的码字作为量化结果,可以用较少的码字表示输入数据,从而实现数据的压缩。同一个码字能够代表多个相似的多维向量,从而实现了**多对一的映射**。
|
||||
@ -416,14 +412,65 @@ $$
|
||||
|
||||
|
||||
|
||||
#### FCM算法时间复杂度分析
|
||||
|
||||
网络节点数目为 $n$(不是矩阵的维度!),聚类簇数$K$
|
||||
|
||||
**初始化步骤**
|
||||
|
||||
- 初始化簇中心和隶属度矩阵 $U$:需要 $O(nK)$
|
||||
|
||||
**更新隶属度**
|
||||
|
||||
- 每个数据点 $a_{ij}$ 计算与每个簇中心 $c_k$ 的距离:$O(K)$
|
||||
- 更新所有数据点的隶属度矩阵:$O(nK^2)$
|
||||
|
||||
**更新簇中心**
|
||||
|
||||
- 计算每个簇的新中心(加权平均):$O(nK)$
|
||||
- 总体簇中心更新:$O(nK)$
|
||||
|
||||
**判断收敛**
|
||||
|
||||
计算簇中心变化量 $\Delta C$:$O(K)$
|
||||
|
||||
**量化处理**
|
||||
|
||||
将元素分配到簇并替换值:$O(nK)$
|
||||
|
||||
**每次迭代的总时间复杂度:**
|
||||
$$
|
||||
O(nK^2) + O(nK) + O(K) \approx O(nK^2)
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
- $n$:数据点数量
|
||||
- $K$:簇数量
|
||||
|
||||
|
||||
|
||||
**如果初始簇中心选取优化方法**
|
||||
|
||||
- 选择 $K$ 个簇中心时:
|
||||
- 需要计算候选集内元素间最小距离
|
||||
- 每次选择复杂度:$O(n^2)$
|
||||
- 总体选择复杂度:$O(Kn^2)$
|
||||
|
||||
整个FCM时间复杂度:$O(Kn^2)+O(TnK^2)$,$T$为迭代次数
|
||||
|
||||
|
||||
|
||||
### 网络重构
|
||||
|
||||
对称非负矩阵分解(SNMF)来构造网络的低维嵌入表示,从而实现对高维网络邻接矩阵的精确重构。
|
||||
对称非负矩阵分解(SNMF)来构造网络的**低维嵌入**表示,从而实现对高维网络邻接矩阵的精确重构。
|
||||
|
||||
低维指的是分解后的$U$矩阵维度小->秩小->重构后的矩阵秩也小。
|
||||
$$
|
||||
A \approx U U^T.
|
||||
$$
|
||||
|
||||
只需计算 $U U^T$ 就能重构出 $A$ 的低秩近似版本。如果选择保留全部特征(即 $r = n$),则可以精确还原 $A$;如果只取部分($r < n$),那么重构结果就是 $A$ 的低秩近似。
|
||||
只需计算 $U U^T$ 就能重构出 $A$ 的**低秩**近似版本。如果选择保留全部特征(即 $r = n$),则可以精确还原 $A$;如果只取部分($r < n$),那么重构结果就是 $A$ 的低秩近似。
|
||||
|
||||
#### 节点移动模型
|
||||
|
||||
@ -487,7 +534,7 @@ $$
|
||||
|
||||
**1. 初始步骤:构造 $B$ 和 $Q$**
|
||||
|
||||
首先对 $A$ 做谱分解,得到(已知结果):
|
||||
首先*对 $A$ 做谱分解*,*或者卡尔曼滤波预测*得到(已知结果):
|
||||
|
||||
- 特征值:$\lambda_1=4, \lambda_2=2$
|
||||
|
||||
@ -583,13 +630,63 @@ A \approx U U^T.
|
||||
$$
|
||||
此时 $U$(尺寸为 $2 \times 2$ 的矩阵)就是对 $A$ 进行低维嵌入得到的“特征表示”,它不仅满足非负性,而且通过内积 $U U^T$ 能近似重构出原矩阵 $A$。
|
||||
|
||||
|
||||
|
||||
#### **时间复杂度分析**
|
||||
|
||||
(1) 初始构造阶段(假设特征值 特征向量已提前获取,不做分析)
|
||||
|
||||
**构造矩阵** $B = X\Lambda^{1/2}$
|
||||
|
||||
$X$ 是 $n \times r$,$\Lambda^{1/2}$ 是 $r \times r$ 对角矩阵。
|
||||
|
||||
$$\mathcal{O}(nr^2) \quad (r \ll n)$$
|
||||
|
||||
|
||||
|
||||
(2) 迭代过程
|
||||
|
||||
**计算 $U = \max(0, B Q)$**
|
||||
|
||||
$B$ 是 $n \times r$,$Q$ 是 $r \times r$。
|
||||
|
||||
$\mathcal{O}(n r^2)$
|
||||
|
||||
**计算 $F = U^T B$**
|
||||
|
||||
$U^T$ 是 $r \times n$,$B$ 是 $n \times r$。
|
||||
|
||||
$\mathcal{O}(n r^2)$
|
||||
|
||||
**对 $F$ 进行 SVD**
|
||||
|
||||
$F$ 是 $r \times r$ 的矩阵。
|
||||
|
||||
SVD 的时间复杂度:$\mathcal{O}(r^3)$。
|
||||
|
||||
**更新 $Q = V H^T$**
|
||||
|
||||
$V$ 和 $H$ 是 $r \times r$。
|
||||
|
||||
$\mathcal{O}(r^3)$
|
||||
|
||||
|
||||
|
||||
(3) 由于通常 $n \gg r$,$\mathcal{O}(n r^2)$ 是主导项,故总复杂度(其中 $T$ 为迭代次数)
|
||||
$$
|
||||
T \cdot \mathcal{O}(nr^2)
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
**两种求对称非负矩阵分解的方法**
|
||||
|
||||
1. **纯梯度下降**
|
||||
- 优点:实现原理简单,对任意大小/形状的矩阵都能做。
|
||||
- 缺点:收敛速度有时较慢,且对初始值敏感。
|
||||
|
||||
2. **rEVD + 旋转截断**
|
||||
2. **rEVD + 旋转截断** (示例方法)
|
||||
- 优点:利用了特征分解,可以先一步把主要信息“压缩”进 $B$,后续只需解决“如何把负数修正掉”以及“如何微调逼近”。
|
||||
- 缺点:需要先做特征分解,适合于对称矩阵或低秩场景。
|
||||
|
||||
|
||||
20
科研/颜佳佳论文.md
20
科研/颜佳佳论文.md
@ -1,2 +1,22 @@
|
||||
## 颜佳佳论文
|
||||
|
||||
### 网络结构优化
|
||||
|
||||
**直接SNMF分解(无优化)**
|
||||
|
||||
- **输入矩阵**:原始动态网络邻接矩阵 $A$(可能稠密或高秩)
|
||||
- **处理流程**:
|
||||
- 直接对称非负矩阵分解:$A \approx UU^T$
|
||||
- 通过迭代调整$U$和旋转矩阵$Q$逼近目标
|
||||
- **存在问题**:
|
||||
- 高秩矩阵需要保留更多特征值($\kappa$较大)
|
||||
- **非稀疏矩阵计算效率低**
|
||||
|
||||
**先优化再SNMF(论文方法)**
|
||||
|
||||
- **优化阶段**(ADMM):
|
||||
- 目标函数:$\min_{A_{\text{opt}}} (1-\alpha)\|A_{\text{opt}}\|_* + \alpha\|A_{\text{opt}}\|_1$
|
||||
- 输出优化矩阵$A_{\text{opt}}$
|
||||
- **SNMF阶段**:
|
||||
- 输入变为优化后的$A_{\text{opt}}$
|
||||
- 保持相同分解流程但效率更高
|
||||
|
||||
92
自学/JAVA面试题.md
Normal file
92
自学/JAVA面试题.md
Normal file
@ -0,0 +1,92 @@
|
||||
## JAVA面试题(1)
|
||||
|
||||
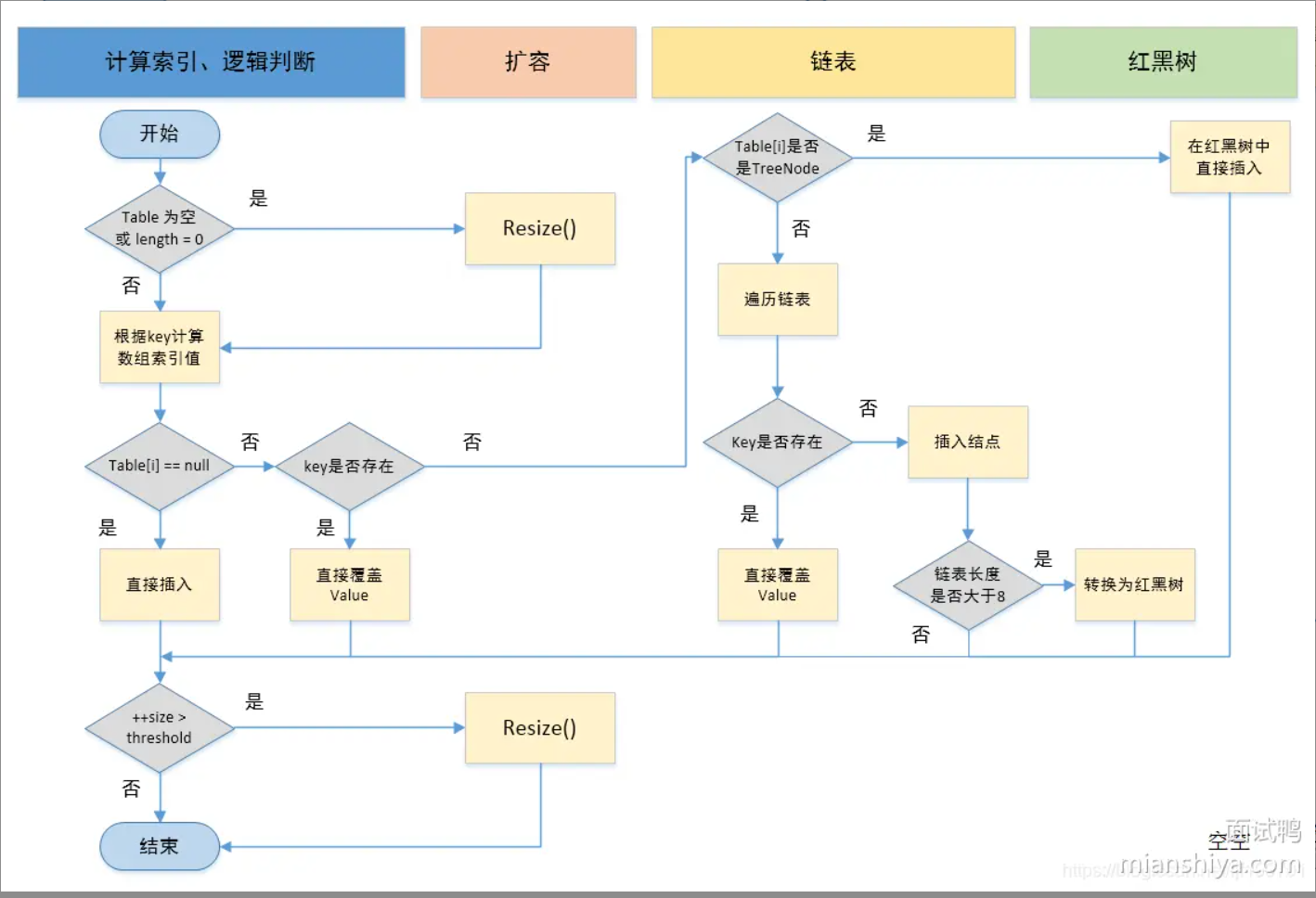
### [说说 Java 中 HashMap 的原理?](https://www.mianshiya.com/bank/1860871861809897474/question/1834107117591187457)
|
||||
|
||||
|
||||
|
||||
**为什么引入红黑树:**
|
||||
当hash冲突较多的时候,链表中的元素会增多,插入、删除、查询的效率会变低,退化成O(n)使用红黑树可以优化插入、删除、查询的效率,logN级别。
|
||||
|
||||
转换时机:
|
||||
链表上的元素个数大于等于8 且 数组长度大于等于64;
|
||||
链表上的元素个数小于等于6的时候,红黑树退化成链表。
|
||||
|
||||
|
||||
|
||||
**链表插入方式变更:从"头插法"改为"尾插法"**
|
||||
|
||||
- **头插法特点**:
|
||||
- 插入时不需要遍历链表
|
||||
- 直接替换头结点
|
||||
- 扩容时会导致链表逆序
|
||||
- 多线程环境下可能产生**死循环**
|
||||
|
||||
- **尾插法改进**:
|
||||
- 避免扩容时的链表逆序
|
||||
- 解决多线程环境下的潜在死循环问题
|
||||
|
||||
|
||||
|
||||
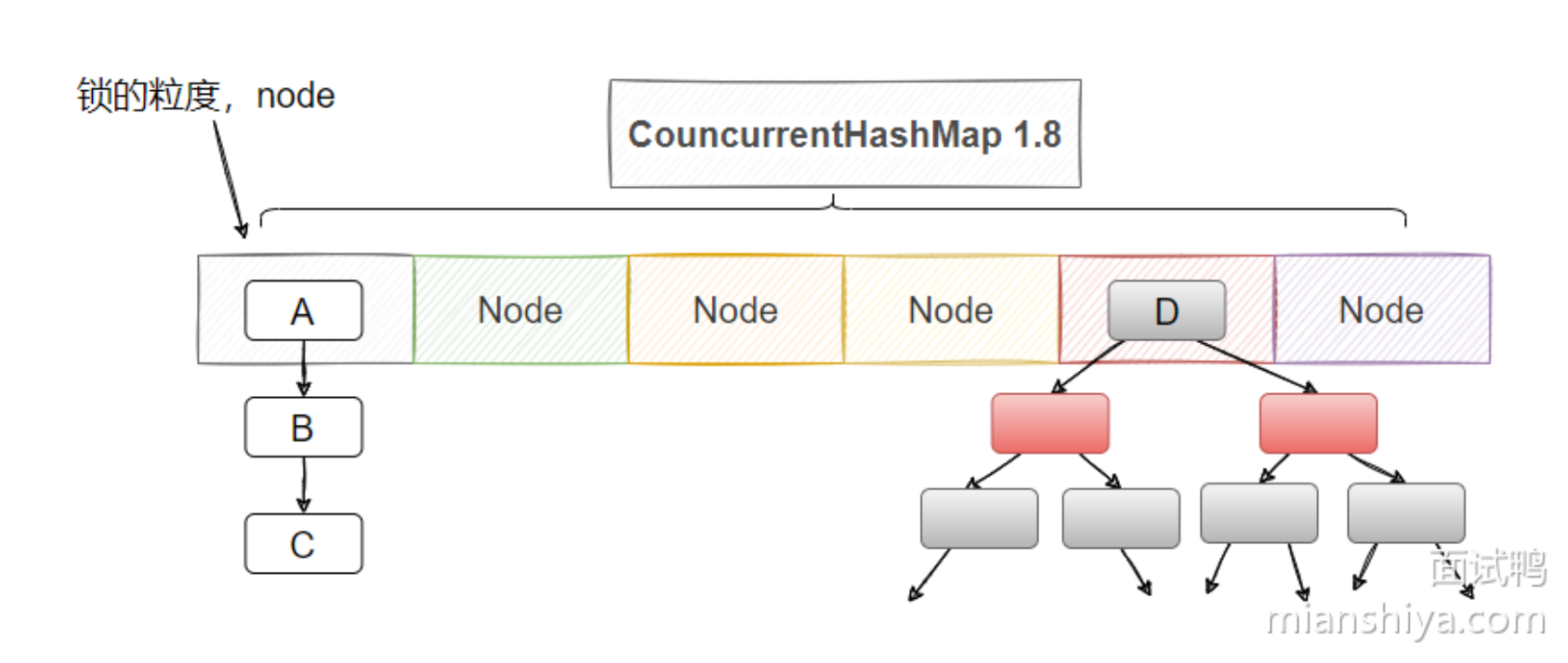
### [Java 中 ConcurrentHashMap 1.7 和 1.8 之间有哪些区别?](https://www.mianshiya.com/bank/1860871861809897474/question/1780933294813114369)
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
#### ConcurrentHashMap 不同JDK版本的实现对比
|
||||
|
||||
1. **数据结构**
|
||||
|
||||
- JDK1.7:
|
||||
- 使用 `Segment(分段锁) + HashEntry数组 + 链表` 的数据结构
|
||||
|
||||
- JDK1.8及之后:
|
||||
- 使用 `数组 + 链表/红黑树` 的数据结构(与HashMap类似)
|
||||
|
||||
2. **锁的类型与宽度**
|
||||
|
||||
- JDK1.7:
|
||||
- 分段锁(Segment)继承了 `ReentrantLock`
|
||||
- Segment容量默认16,不会扩容 → 默认支持16个线程并发访问
|
||||
|
||||
- JDK1.8:
|
||||
- 使用 `synchronized + CAS` 保证线程安全
|
||||
- 空节点:通过CAS添加(**put操作**,多个线程可能同时想要将一个新的键值对插入到同一个桶中,这时它们会使用 CAS 来比较当前桶中的元素(或节点)是否已经被修改过。)
|
||||
- 非空节点:通过synchronized加锁,**只锁住该桶**,其他桶可以并行访问。
|
||||
|
||||
3. **渐进式扩容(JDK1.8+)**
|
||||
|
||||
- **触发条件**:元素数量 ≥ `数组容量 × 负载因子(默认0.75)`
|
||||
- **扩容过程**:
|
||||
1. 创建2倍大小的新数组
|
||||
2. 线程操作数据时,逐步迁移旧数组数据到新数组
|
||||
3. 使用 `transferIndex` 标记迁移进度
|
||||
4. 直到旧数组数据完全迁移完成
|
||||
|
||||
|
||||
|
||||
### [500. 什么是 Java 的 CAS(Compare-And-Swap)操作?](https://www.mianshiya.com/question/1780933295027023873)
|
||||
|
||||
CAS操作包含三个基本操作数:
|
||||
|
||||
1. **内存位置(V)**:要更新的变量
|
||||
2. **预期原值(A)**:认为变量当前应该具有的值
|
||||
3. **新值(B)**:想要更新为的值
|
||||
|
||||
CAS 工作原理:
|
||||
|
||||
1. 读取内存位置V的当前值为A
|
||||
2. 计算新值B
|
||||
3. 当且仅当V的值等于A时,将V的值设置为B
|
||||
4. 如果不等于A,则操作失败(通常重试)
|
||||
|
||||
```text
|
||||
伪代码表示:
|
||||
if (V == A) {
|
||||
V = B;
|
||||
return true;
|
||||
} else {
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
@ -407,7 +407,7 @@ public class DeptController {
|
||||
|
||||
### 快速启动
|
||||
|
||||
1. 新建spring initializr module
|
||||
1. 新建**spring initializr** project
|
||||
2. 删除以下文件
|
||||
|
||||
|
||||
@ -1239,6 +1239,18 @@ public class SpringbootWebConfig2Application {
|
||||
|
||||
9. lombok的相关注解。非常实用的工具库。
|
||||
|
||||
- 在pom.xml文件中引入依赖
|
||||
|
||||
```xml
|
||||
<!-- 在springboot的父工程中,已经集成了lombok并指定了版本号,故当前引入依赖时不需要指定version -->
|
||||
<dependency>
|
||||
<groupId>org.projectlombok</groupId>
|
||||
<artifactId>lombok</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
- 在实体类上添加以下注解(加粗为常用)
|
||||
|
||||
| **注解** | **作用** |
|
||||
| ----------------------- | ------------------------------------------------------------ |
|
||||
| @Getter/@Setter | 为所有的属性提供get/set方法 |
|
||||
@ -1300,32 +1312,31 @@ public class SpringbootWebConfig2Application {
|
||||
|
||||
|
||||
|
||||
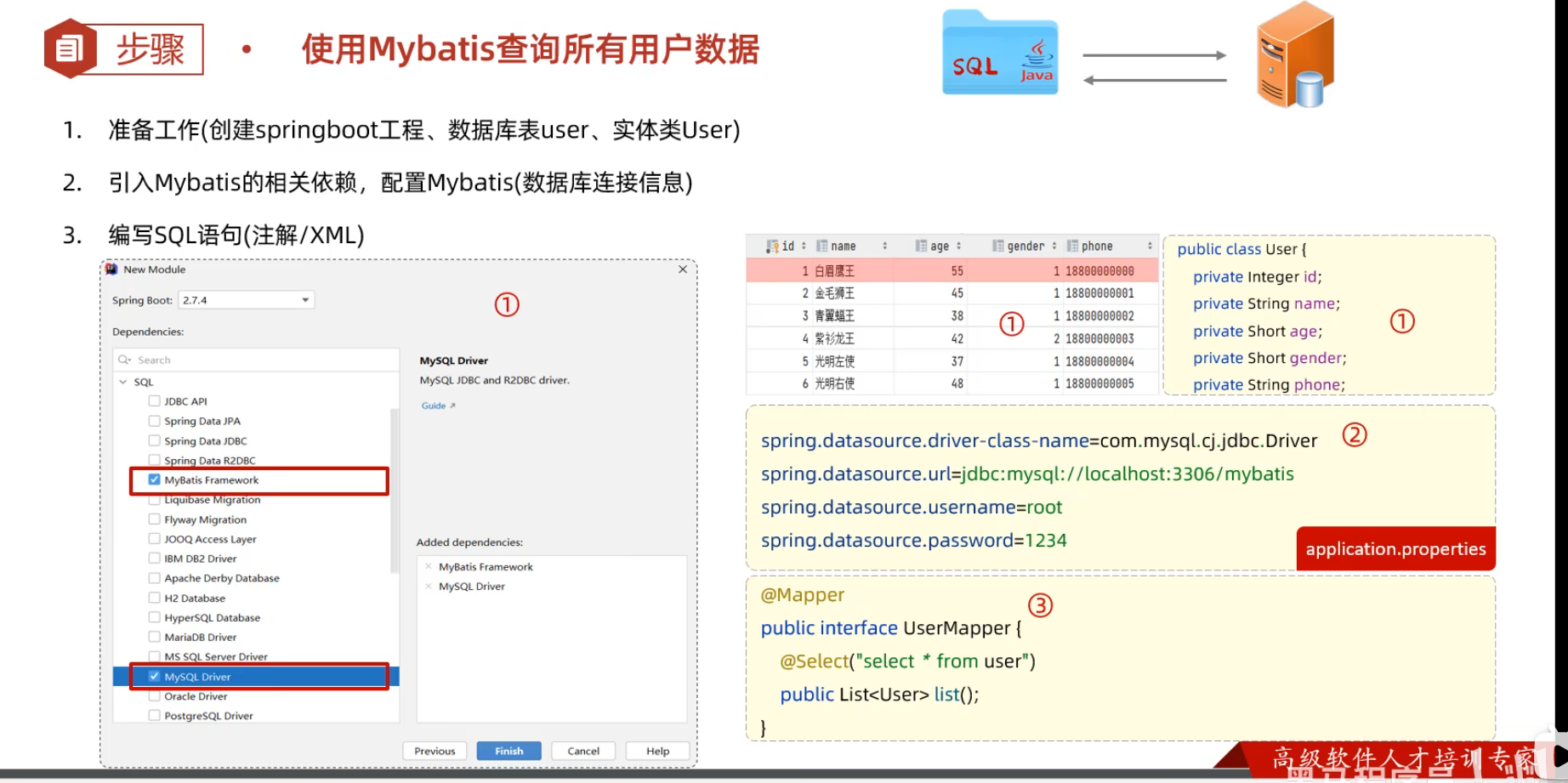
1. 创建springboot工程,并导入 mybatis的起步依赖、mysql的驱动包。创建用户表user,并创建对应的实体类User
|
||||
|
||||
|
||||
1. 创建springboot工程(Spring Initializr),并导入 mybatis的起步依赖、mysql的驱动包。创建用户表user,并创建对应的实体类User
|
||||

|
||||
|
||||
2. 在springboot项目中,可以编写main/resources/application.properties文件,配置数据库连接信息。
|
||||
|
||||
```java
|
||||
#驱动类名称
|
||||
spring.datasource.driver-class-name=com.mysql.cj.jdbc.Driver
|
||||
#数据库连接的url
|
||||
spring.datasource.url=jdbc:mysql://localhost:3306/mybatis
|
||||
#连接数据库的用户名
|
||||
spring.datasource.username=root
|
||||
#连接数据库的密码
|
||||
spring.datasource.password=1234
|
||||
```
|
||||
```
|
||||
#驱动类名称
|
||||
spring.datasource.driver-class-name=com.mysql.cj.jdbc.Driver
|
||||
#数据库连接的url
|
||||
spring.datasource.url=jdbc:mysql://localhost:3306/mybatis
|
||||
#连接数据库的用户名
|
||||
spring.datasource.username=root
|
||||
#连接数据库的密码
|
||||
spring.datasource.password=1234
|
||||
```
|
||||
|
||||
3. 在引导类所在包下,在创建一个包 mapper。在mapper包下创建一个接口 UserMapper
|
||||
|
||||
|
||||

|
||||
|
||||
@Mapper注解:表示是mybatis中的Mapper接口
|
||||
|
||||
- 程序运行时:框架会自动生成接口的**实现类对象(代理对象)**,并交给Spring的IOC容器管理
|
||||
-程序运行时:框架会自动生成接口的**实现类对象(代理对象)**,并交给Spring的IOC容器管理
|
||||
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
@ -1336,49 +1347,69 @@ public interface UserMapper {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 数据库连接池
|
||||
|
||||
数据库连接池是个容器,负责分配、管理数据库**连接(Connection)**
|
||||
数据库连接池是一个容器,负责管理和分配数据库连接(`Connection`)。
|
||||
|
||||
- 程序在启动时,会在数据库连接池(容器)中,创建一定数量的Connection对象
|
||||
- 在程序启动时,连接池会创建一定数量的数据库连接。
|
||||
- 客户端在执行 SQL 时,从连接池获取连接对象,执行完 SQL 后,将连接归还给连接池,以供其他客户端复用。
|
||||
- 如果连接对象长时间空闲且超过预设的最大空闲时间,连接池会自动释放该连接。
|
||||
|
||||
允许应用程序重复使用一个现有的数据库连接,而不是再重新建立一个
|
||||
**优势**:避免频繁创建和销毁连接,提高数据库访问效率。
|
||||
|
||||
- 客户端在执行SQL时,先从连接池中获取一个Connection对象,然后在执行SQL语句,SQL语句执行完之后,释放Connection时就会把Connection对象归还给连接池(Connection对象可以复用)
|
||||
|
||||
- 客户端获取到Connection对象了,但是Connection对象并没有去访问数据库(处于空闲),数据库连接池发现Connection对象的空闲时间 > 连接池中预设的最大空闲时间,此时数据库连接池就会自动释放掉这个连接对象
|
||||
|
||||
### lombok
|
||||
Druid(德鲁伊)
|
||||
|
||||
Lombok是一个实用的Java类库,可以通过简单的注解来简化和消除一些必须有但显得很臃肿的Java代码。
|
||||
* Druid连接池是阿里巴巴开源的数据库连接池项目
|
||||
|
||||
| **注解** | **作用** |
|
||||
| ------------------- | ------------------------------------------------------------ |
|
||||
| @Getter/@Setter | 为所有的属性提供get/set方法 |
|
||||
| @ToString | 会给类自动生成易阅读的 toString 方法 |
|
||||
| @EqualsAndHashCode | 根据类所拥有的非静态字段自动重写 equals 方法和 hashCode 方法 |
|
||||
| **@Data** | **提供了更综合的生成代码功能(@Getter + @Setter + @ToString + @EqualsAndHashCode)** |
|
||||
| @NoArgsConstructor | 为实体类生成无参的构造器方法 |
|
||||
| @AllArgsConstructor | 为实体类生成除了static修饰的字段之外带有各参数的构造器方法。 |
|
||||
* 功能强大,性能优秀,是Java语言最好的数据库连接池之一
|
||||
|
||||
**使用**
|
||||
把默认的 Hikari 数据库连接池切换为 Druid 数据库连接池:
|
||||
|
||||
1. 在pom.xml文件中引入依赖
|
||||
|
||||
```xml
|
||||
<dependency>
|
||||
<!-- Druid连接池依赖 -->
|
||||
<groupId>com.alibaba</groupId>
|
||||
<artifactId>druid-spring-boot-starter</artifactId>
|
||||
<version>1.2.8</version>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2. 在application.properties中引入数据库连接配置
|
||||
|
||||
```properties
|
||||
spring.datasource.druid.driver-class-name=com.mysql.cj.jdbc.Driver
|
||||
spring.datasource.druid.url=jdbc:mysql://localhost:3306/mybatis
|
||||
spring.datasource.druid.username=root
|
||||
spring.datasource.druid.password=1234
|
||||
```
|
||||
|
||||
|
||||
|
||||
### SQL注入问题
|
||||
|
||||
SQL注入:由于没有对用户输入进行充分检查,而SQL又是拼接而成,在用户输入参数时,在参数中添加一些SQL关键字,达到改变SQL运行结果的目的,也可以完成恶意攻击。
|
||||
|
||||
在Mybatis中提供的参数占位符有两种:${...} 、#{...}
|
||||
|
||||
- #{...}
|
||||
- 执行SQL时,会将#{…}替换为?,生成预编译SQL,会自动设置参数值
|
||||
- 使用时机:参数传递,都使用#{…}
|
||||
|
||||
- ${...}
|
||||
- 拼接SQL。直接将参数拼接在SQL语句中,**存在SQL注入问题**
|
||||
- 使用时机:如果对表名、列表进行动态设置时使用
|
||||
|
||||
```java
|
||||
import lombok.Data;
|
||||
|
||||
@Data
|
||||
public class User {
|
||||
private Integer id;
|
||||
private String name;
|
||||
private Short age;
|
||||
private Short gender;
|
||||
private String phone;
|
||||
}
|
||||
```
|
||||
|
||||
### 日志输出
|
||||
|
||||
在Mybatis当中我们可以借助日志,查看到sql语句的执行、执行传递的参数以及执行结果。
|
||||
只建议开发环境使用:在Mybatis当中我们可以借助日志,查看到sql语句的执行、执行传递的参数以及执行结果
|
||||
|
||||
1. 打开application.properties文件
|
||||
|
||||
@ -1391,11 +1422,55 @@ mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
|
||||
|
||||
|
||||
|
||||
### 驼峰命名法
|
||||
|
||||
在 Java 项目中,数据库表字段名一般使用 **下划线命名法**(snake_case),而 Java 中的变量名使用 **驼峰命名法**(camelCase)。
|
||||
|
||||
- [x] **小驼峰命名(lowerCamelCase)**:
|
||||
|
||||
- 第一个单词的首字母小写,后续单词的首字母大写。
|
||||
- **例子**:`firstName`, `userName`, `myVariable`
|
||||
|
||||
**大驼峰命名(UpperCamelCase)**:
|
||||
|
||||
- 每个单词的首字母都大写,通常用于类名或类型名。
|
||||
- **例子**:`MyClass`, `EmployeeData`, `OrderDetails`
|
||||
|
||||
|
||||
|
||||
表中查询的数据封装到实体类中
|
||||
|
||||
- 实体类属性名和数据库表查询返回的**字段名一致**,mybatis会自动封装。
|
||||
- 如果实体类属性名和数据库表查询返回的字段名不一致,不能自动封装。
|
||||
|
||||

|
||||
|
||||
解决方法:
|
||||
|
||||
1. 起别名
|
||||
2. 结果映射
|
||||
3. **开启驼峰命名**
|
||||
4. **属性名和表中字段名保持一致**
|
||||
|
||||
|
||||
|
||||
**开启驼峰命名(推荐)**:如果字段名与属性名符合驼峰命名规则,mybatis会自动通过驼峰命名规则映射
|
||||
|
||||
> 驼峰命名规则: abc_xyz => abcXyz
|
||||
>
|
||||
> - 表中字段名:abc_xyz
|
||||
> - 类中属性名:abcXyz
|
||||
|
||||
```java
|
||||
# 在application.properties中添加:
|
||||
mybatis.configuration.map-underscore-to-camel-case=true
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 增删改
|
||||
|
||||
- **增删改通用!:返回值为int时,表示影响的记录数,一般不需要可以设置为void!**
|
||||
- **#{} 表示占位符**,执行SQL时,生成预编译SQL,会自动设置参数值
|
||||
- ${} 也是占位符,但直接将参数拼接在SQL语句中,存在SQL注入问题
|
||||
|
||||
**作用于单个字段**
|
||||
|
||||
@ -1431,45 +1506,23 @@ public interface EmpMapper {
|
||||
}
|
||||
```
|
||||
|
||||
说明:#{...} 里面写的名称是对象的**属性名**!,函数内的参数是Emp对象
|
||||
在 **`@Insert`** 注解中使用 `#{}` 来引用 `Emp` 对象的属性,MyBatis 会自动从 `Emp` 对象中提取相应的字段并绑定到 SQL 语句中的占位符。
|
||||
|
||||
useGeneratedKeys = true表示获取返回的主键值,keyProperty = "id"表示主键值存在Emp对象的id属性中,添加这句可以直接获取主键值
|
||||
`@Options(useGeneratedKeys = true, keyProperty = "id")` 这行配置表示,插入时自动生成的主键会赋值给 `Emp` 对象的 `id` 属性。
|
||||
|
||||
```
|
||||
// 调用 mapper 执行插入操作
|
||||
empMapper.insert(emp);
|
||||
|
||||
|
||||
### 查/驼峰命名法
|
||||
|
||||
表中查询的数据封装到实体类中
|
||||
|
||||
- 实体类属性名和数据库表查询返回的字段名一致,mybatis会自动封装。
|
||||
- 如果实体类属性名和数据库表查询返回的字段名不一致,不能自动封装。
|
||||
|
||||

|
||||
|
||||
解决方法:
|
||||
|
||||
1. 起别名
|
||||
2. 结果映射
|
||||
3. **开启驼峰命名**
|
||||
4. **属性名和表中字段名保持一致**
|
||||
|
||||
**开启驼峰命名(推荐)**:如果字段名与属性名符合驼峰命名规则,mybatis会自动通过驼峰命名规则映射
|
||||
|
||||
> 驼峰命名规则: abc_xyz => abcXyz
|
||||
>
|
||||
> - 表中字段名:abc_xyz
|
||||
>- 类中属性名:abcXyz
|
||||
|
||||
```java
|
||||
# 在application.properties中添加:
|
||||
mybatis.configuration.map-underscore-to-camel-case=true
|
||||
// 现在 emp 对象的 id 属性会被自动设置为数据库生成的主键值
|
||||
System.out.println("Generated ID: " + emp.getId());
|
||||
```
|
||||
|
||||
> 要使用驼峰命名前提是 实体类的属性 与 数据库表中的字段名严格遵守驼峰命名。
|
||||
|
||||
|
||||
### 查
|
||||
|
||||
eg:通过页面原型以及需求描述我们要实现的查询:
|
||||
查询案例:
|
||||
|
||||
- **姓名:要求支持模糊匹配**
|
||||
- 性别:要求精确匹配
|
||||
@ -1480,6 +1533,12 @@ eg:通过页面原型以及需求描述我们要实现的查询:
|
||||
|
||||
解决方案:
|
||||
|
||||
使用MySQL提供的字符串拼接函数:`concat('%' , '关键字' , '%')`
|
||||
|
||||
**`CONCAT()`** 如果其中任何一个参数为 **`NULL`**,`CONCAT()` 返回 **`NULL`**,`Like NULL`会导致查询不到任何结果!
|
||||
|
||||
`NULL`和`''`是完全不同的
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface EmpMapper {
|
||||
@ -1494,8 +1553,6 @@ public interface EmpMapper {
|
||||
}
|
||||
```
|
||||
|
||||
**使用MySQL提供的字符串拼接函数:concat('%' , '关键字' , '%')**
|
||||
|
||||
|
||||
|
||||
### XML配置文件规范
|
||||
@ -1514,7 +1571,7 @@ public interface EmpMapper {
|
||||
|
||||
\<select>标签:就是用于编写select查询语句的。
|
||||
|
||||
- resultType属性,指的是查询返回的单条记录所封装的类型。
|
||||
resultType属性,指的是查询返回的单条记录所封装的类型。
|
||||
|
||||
|
||||
|
||||
@ -1522,21 +1579,23 @@ public interface EmpMapper {
|
||||
|
||||
1. resources下创与java下一样的包,即edu/whut/mapper,新建xx.xml文件
|
||||
|
||||
2. ```text
|
||||
2. 配置Mapper文件
|
||||
|
||||
```xml
|
||||
<?xml version="1.0" encoding="UTF-8" ?>
|
||||
<!DOCTYPE mapper
|
||||
PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN"
|
||||
"https://mybatis.org/dtd/mybatis-3-mapper.dtd">
|
||||
<mapper namespace="edu.whut.mapper.EmpMapper">
|
||||
|
||||
<!-- SQL 查询语句写在这里 -->
|
||||
</mapper>
|
||||
|
||||
XML映射文件的namespace属性为Mapper接口**全限定名**(包+类名)
|
||||
```
|
||||
|
||||
`namespace` 属性指定了 **Mapper 接口的全限定名**(即包名 + 类名)。
|
||||
|
||||
3. 编写查询语句
|
||||
|
||||
3. ```text
|
||||
```xml
|
||||
<select id="list" resultType="edu.whut.pojo.Emp">
|
||||
select * from emp
|
||||
where name like concat('%',#{name},'%')
|
||||
@ -1546,15 +1605,17 @@ public interface EmpMapper {
|
||||
</select>
|
||||
```
|
||||
|
||||
XML映射文件中sql语句的id与Mapper接口中的**方法名**一致,并保持**返回类型一致**(也是**全限定名**!!).里面的查询语句与之前的一模一样,仅仅单独写到一个xml文件中罢了。
|
||||
|
||||
**注意:**返回类型指的是单挑记录的类型,是Emp,不是list<Emp>
|
||||
**`id="list"`**:指定查询方法的名称,应该与 Mapper 接口中的方法名称一致。
|
||||
|
||||
**`resultType="edu.whut.pojo.Emp"`**:`resultType` 只在 **查询操作** 中需要指定。指定查询结果映射的对象类型,这里是 `Emp` 类。
|
||||
|
||||
|
||||
|
||||
**这里有bug!!!concat('%',#{name},'%')这里应该用<where> <if>标签对name是否为''或null进行判断**
|
||||
这里有bug!!!
|
||||
|
||||
`concat('%',#{name},'%')`这里应该用`<where>` `<if>`标签对name是否为`NULL`或`''`进行判断
|
||||
|
||||
|
||||
`''`和`null`虽然在某些上下文中可能看起来相似,但它们代表了不同的概念:一个是具有明确的(虽然是空的)值,另一个是完全没有值。
|
||||
|
||||
### 动态SQL
|
||||
|
||||
@ -1570,8 +1631,6 @@ public interface EmpMapper {
|
||||
|
||||
`<where>`只会在子元素有内容的情况下才插入where子句,而且会自动去除子句的开头的AND或OR,**加了总比不加好**
|
||||
|
||||
|
||||
|
||||
```java
|
||||
<select id="list" resultType="com.itheima.pojo.Emp">
|
||||
select * from emp
|
||||
@ -1591,9 +1650,11 @@ public interface EmpMapper {
|
||||
</select>
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### SQL-foreach
|
||||
|
||||
mapper接口:
|
||||
Mapper 接口
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
@ -1603,9 +1664,9 @@ public interface EmpMapper {
|
||||
}
|
||||
```
|
||||
|
||||
xml:
|
||||
XML 映射文件
|
||||
|
||||
语法:
|
||||
`<foreach>` 标签用于遍历集合,常用于动态生成 SQL 语句中的 IN 子句、批量插入、批量更新等操作。
|
||||
|
||||
```java
|
||||
<foreach collection="集合名称" item="集合遍历出来的元素/项" separator="每一次遍历使用的分隔符"
|
||||
@ -1613,17 +1674,23 @@ xml:
|
||||
</foreach>
|
||||
```
|
||||
|
||||
`open="("`:这个属性表示,在*生成的 SQL 语句开始*时添加一个 左括号 `(`。
|
||||
|
||||
`close=")"`:这个属性表示,在生成的 SQL 语句结束时添加一个 右括号 `)`。
|
||||
|
||||
例:批量删除实现
|
||||
|
||||
```java
|
||||
<delete id="deleteByIds">
|
||||
delete from emp where id in
|
||||
<foreach collection="ids" item="id" separator="," open="(" close=")">
|
||||
#{id}
|
||||
</foreach>
|
||||
</delete>
|
||||
DELETE FROM emp WHERE id IN
|
||||
<foreach collection="ids" item="id" separator="," open="(" close=")">
|
||||
#{id}
|
||||
</foreach>
|
||||
</delete>
|
||||
```
|
||||
|
||||
实现效果类似:`DELETE FROM emp WHERE id IN (1, 2, 3);`
|
||||
|
||||
|
||||
|
||||
## 案例实战
|
||||
@ -1642,15 +1709,42 @@ xml:
|
||||
|
||||
分页插件帮我们完成了以下操作:
|
||||
|
||||
1. 先获取到要执行的SQL语句:select * from emp
|
||||
2. 把SQL语句中的字段列表,变为:count(*)
|
||||
3. 执行SQL语句:select count(*) from emp //获取到总记录数
|
||||
4. 再对要执行的SQL语句:select * from emp 进行改造,在末尾添加 limit ? , ?
|
||||
5. 执行改造后的SQL语句:select * from emp limit ? , ?
|
||||
1. 先获取到要执行的SQL语句:
|
||||
|
||||
```
|
||||
select * from emp
|
||||
```
|
||||
|
||||
2. 为了实现分页,第一步是获取符合条件的总记录数。分页插件将原始 SQL 查询中的 `SELECT *` 改成 `SELECT count(*)`
|
||||
|
||||
```mysql
|
||||
select count(*) from emp;
|
||||
```
|
||||
|
||||
3. 一旦知道了总记录数,分页插件会将 `SELECT *` 的查询语句进行修改,加入 `LIMIT` 关键字,限制返回的记录数。
|
||||
|
||||
```mysql
|
||||
select * from emp limit ?, ?
|
||||
```
|
||||
|
||||
第一个参数(`?`)是 起始位置,通常是 `(当前页 - 1) * 每页显示的记录数`,即从哪一行开始查询。
|
||||
|
||||
第二个参数(`?`)是 每页显示的记录数,即返回多少条数据。
|
||||
|
||||
4. 执行分页查询,例如,假设每页显示 10 条记录,你请求第 2 页数据,那么 SQL 语句会变成:
|
||||
|
||||
```mysql
|
||||
select * from emp limit 10, 10;
|
||||
```
|
||||
|
||||
|
||||
|
||||
**使用方法:**
|
||||
|
||||
当使用了PageHelper分页插件进行分页,就**无需再Mapper中进行手动分页**了。 在Mapper中我们只需要进行正常的列表查询即可。在Service层中,调用Mapper的方法之前**设置分页参数**,在调用Mapper方法执行查询之后,解析分页结果,并将结果封装到PageBean对象中返回。
|
||||
当使用 **PageHelper** 分页插件时,无需在 Mapper 中手动处理分页。只需在 Mapper 中编写常规的列表查询。
|
||||
|
||||
- 在 **Service 层**,调用 Mapper 方法之前,**设置分页参数**。
|
||||
- 调用 Mapper 查询后,**自动进行分页**,并将结果封装到 `PageBean` 对象中返回。
|
||||
|
||||
1、在pom.xml引入依赖
|
||||
|
||||
@ -1674,6 +1768,7 @@ public interface EmpMapper {
|
||||
```
|
||||
|
||||
3、EmpServiceImpl
|
||||
当调用 `PageHelper.startPage(page, pageSize)` 时,PageHelper 插件会拦截随后的 SQL 查询,自动修改查询,加入 `LIMIT` 子句来实现分页功能。
|
||||
|
||||
```java
|
||||
@Override
|
||||
@ -1732,7 +1827,7 @@ public class EmpController {
|
||||
</if>
|
||||
</where>
|
||||
order by create_time desc
|
||||
</select>
|
||||
/select>
|
||||
```
|
||||
|
||||
|
||||
|
||||
197
自学/Mysql数据库.md
197
自学/Mysql数据库.md
@ -186,11 +186,11 @@ desc tb_tmps; ( tb_tmps为表名)
|
||||
|
||||
```mysql
|
||||
create table 表名(
|
||||
字段1 字段1类型 [约束] [comment 字段1注释 ],
|
||||
字段2 字段2类型 [约束] [comment 字段2注释 ],
|
||||
字段1 字段1类型 [约束] [comment '字段1注释' ],
|
||||
字段2 字段2类型 [约束] [comment '字段2注释' ],
|
||||
......
|
||||
字段n 字段n类型 [约束] [comment 字段n注释 ]
|
||||
) [ comment 表注释 ] ;
|
||||
字段n 字段n类型 [约束] [comment '字段n注释' ]
|
||||
) [ comment '表注释' ] ;
|
||||
```
|
||||
|
||||
> 注意: [ ] 中的内容为可选参数; 最后一个字段后面没有逗号
|
||||
@ -215,29 +215,56 @@ create table tb_user (
|
||||
| ------------ | ------------------------------------------------ | ----------- |
|
||||
| 非空约束 | 限制该字段值不能为null | not null |
|
||||
| 唯一约束 | 保证字段的所有数据都是唯一、不重复的 | unique |
|
||||
| 主键约束 | 主键是一行数据的唯一标识,要求非空且唯一 | primary key |
|
||||
| 主键约束 | 主键是一行数据的唯一标识,要求**非空且唯一** | primary key |
|
||||
| 默认约束 | 保存数据时,如果未指定该字段值,则采用默认值 | default |
|
||||
| **外键约束** | 让两张表的数据建立连接,保证数据的一致性和完整性 | foreign key |
|
||||
|
||||
```text
|
||||
create table tb_user (
|
||||
id int primary key auto_increment comment 'ID,唯一标识',
|
||||
username varchar(20) not null unique comment '用户名',
|
||||
name varchar(10) not null comment '姓名',
|
||||
age int comment '年龄',
|
||||
gender char(1) default '男' comment '性别'
|
||||
) comment '用户表';
|
||||
```mysql
|
||||
CREATE TABLE tb_user (
|
||||
id INT PRIMARY KEY AUTO_INCREMENT COMMENT 'ID,唯一标识',
|
||||
username VARCHAR(20) NOT NULL UNIQUE COMMENT '用户名',
|
||||
name VARCHAR(10) NOT NULL COMMENT '姓名',
|
||||
age INT COMMENT '年龄',
|
||||
gender CHAR(1) DEFAULT '男' COMMENT '性别'
|
||||
) COMMENT '用户表';
|
||||
|
||||
-- 假设我们有一个 orders 表,它将 tb_user 表的 id 字段作为外键
|
||||
CREATE TABLE orders (
|
||||
order_id INT PRIMARY KEY AUTO_INCREMENT COMMENT '订单ID',
|
||||
order_date DATE COMMENT '订单日期',
|
||||
user_id INT,
|
||||
FOREIGN KEY (user_id) REFERENCES tb_user(id)
|
||||
ON DELETE CASCADE
|
||||
ON UPDATE CASCADE,
|
||||
COMMENT '订单表'
|
||||
);
|
||||
```
|
||||
|
||||
auto_increment:
|
||||
**foreign key:**
|
||||
|
||||
- 保证数据的一致性和完整性
|
||||
|
||||
- **`ON DELETE CASCADE`**:如果父表中的某行被删除,那么子表中所有与之关联的行也会被自动删除。
|
||||
|
||||
**`ON DELETE SET NULL`**:如果父表中的某行被删除,子表中的相关外键列会被设置为 `NULL`。
|
||||
|
||||
**`ON UPDATE CASCADE`**:如果父表中的外键值被更新,那么子表中的相关外键值也会自动更新。
|
||||
|
||||
注意:在实际的 Java 项目中,特别是在一些微服务架构或分布式系统中,通常**不直接依赖数据库中的外键约束**。相反,开发者通常会在代码中通过逻辑来确保数据的一致性和完整性。
|
||||
|
||||
|
||||
|
||||
**auto_increment:**
|
||||
|
||||
- 每次插入新的行记录时,数据库自动生成id字段(主键)下的值
|
||||
- 具有auto_increment的数据列是一个正数序列开始增长(从1开始自增)
|
||||
- 具有auto_increment的数据列是一个正数序列且整型(从1开始自增)
|
||||
- 不能应用于多个字段
|
||||
|
||||
|
||||
|
||||
**设计表的字段时,还应考虑:**
|
||||
|
||||
id:主键,唯一标志这条记录
|
||||
|
||||
create_time :插入记录的时间 now()函数可以获取当前时间
|
||||
update_time:最后修改记录的时间
|
||||
|
||||
@ -249,6 +276,8 @@ DML英文全称是Data Manipulation Language(数据操作语言),用来对数
|
||||
- 修改数据(UPDATE)
|
||||
- 删除数据(DELETE)
|
||||
|
||||
|
||||
|
||||
### INSERT
|
||||
|
||||
insert语法:
|
||||
@ -277,6 +306,8 @@ insert语法:
|
||||
insert into 表名 values (值1, 值2, ...), (值1, 值2, ...);
|
||||
~~~
|
||||
|
||||
|
||||
|
||||
### UPDATE
|
||||
|
||||
update语法:
|
||||
@ -299,6 +330,8 @@ update tb_emp set entrydate='2010-01-01',update_time=now();
|
||||
|
||||
**注意!**不带where会更新表中所有记录!
|
||||
|
||||
|
||||
|
||||
### DELETE
|
||||
|
||||
delete语法:
|
||||
@ -321,6 +354,8 @@ delete from tb_emp;
|
||||
|
||||
DELETE 语句不能删除某一个字段的值(可以使用UPDATE,将该字段值置为NULL即可)。
|
||||
|
||||
|
||||
|
||||
## DQL(查询)
|
||||
|
||||
DQL英文全称是Data Query Language(数据查询语言),用来查询数据库表中的记录。
|
||||
@ -391,7 +426,20 @@ LIMIT
|
||||
| or 或 \|\| | 或者 (多个条件任意一个成立) |
|
||||
| not 或 ! | 非 , 不是 |
|
||||
|
||||
案例:查询 入职时间 在 '2000-01-01' (包含) 到 '2010-01-01'(包含) 之间 且 性别为女 的员工信息
|
||||
|
||||
|
||||
**表数据**:
|
||||
|
||||
| id | name | gender | job | entrydate |
|
||||
| ---- | ---- | ------ | ---- | ---------- |
|
||||
| 1 | 张三 | 2 | 2 | 2005-04-15 |
|
||||
| 2 | 李四 | 1 | 3 | 2007-07-22 |
|
||||
| 3 | 王五 | 2 | 4 | 2011-09-01 |
|
||||
| 4 | 赵六 | 1 | 2 | 2008-06-11 |
|
||||
|
||||
|
||||
|
||||
案例1:查询 入职时间 在 '2000-01-01' (包含) 到 '2010-01-01'(包含) 之间 且 性别为女 的员工信息
|
||||
|
||||
```text
|
||||
select *
|
||||
@ -400,7 +448,7 @@ where entrydate between '2000-01-01' and '2010-01-01'
|
||||
and gender = 2;
|
||||
```
|
||||
|
||||
案例8:查询 职位是 2 (讲师), 3 (学工主管), 4 (教研主管) 的员工信息
|
||||
案例2:查询 职位是 2 (讲师), 3 (学工主管), 4 (教研主管) 的员工信息
|
||||
|
||||
```text
|
||||
select *
|
||||
@ -408,7 +456,13 @@ from tb_emp
|
||||
where job in (2,3,4);
|
||||
```
|
||||
|
||||
案例9:查询 姓名 为两个字的员工信息
|
||||
案例3:查询 姓名 为两个字的员工信息
|
||||
|
||||
常见的 **LIKE** 模式匹配符包括:
|
||||
|
||||
**`%`**:表示零个或多个字符。
|
||||
|
||||
**`_`**:表示一个字符。
|
||||
|
||||
~~~mysql
|
||||
select *
|
||||
@ -420,19 +474,31 @@ where name like '__'; # 通配符 "_" 代表任意1个字符
|
||||
|
||||
### 聚合函数
|
||||
|
||||
之前我们做的查询都是横向查询,就是根据条件一行一行的进行判断,而使用聚合函数查询就是**纵向查询**,它是对一列的值进行计算,然后返回一个结果值。(将一列数据作为一个整体,进行纵向计算)
|
||||
之前我们做的查询都是**横向查询**,就是根据条件一行一行的进行判断,而使用聚合函数查询就是**纵向查询**,它是对一列的值进行计算,然后**返回一个结果值**。(将一列数据作为一个整体,进行纵向计算)
|
||||
|
||||
**聚合函数:**
|
||||
|
||||
| **函数** | **功能** |
|
||||
| -------- | -------- |
|
||||
| count | 统计数量 |
|
||||
| max | 最大值 |
|
||||
| min | 最小值 |
|
||||
| avg | 平均值 |
|
||||
| sum | 求和 |
|
||||
|
||||
语法:
|
||||
|
||||
~~~mysql
|
||||
select 聚合函数(字段列表) from 表名 ;
|
||||
select 聚合函数(字段名、列名) from 表名 ;
|
||||
~~~
|
||||
|
||||
> 注意 : 聚合函数会忽略空值,对NULL值不作为统计。
|
||||
|
||||
```text
|
||||
```mysql
|
||||
# count(*) 推荐此写法(MySQL底层进行了优化)
|
||||
select count(*) from tb_emp;
|
||||
select count(*) from tb_emp; -- 统计记录数
|
||||
|
||||
SELECT SUM(amount) FROM tb_sales; -- 统计amount列的总金额
|
||||
```
|
||||
|
||||
|
||||
@ -445,10 +511,19 @@ select count(*) from tb_emp;
|
||||
>
|
||||
> 分组查询通常会使用**聚合函数**进行计算。
|
||||
|
||||
```text
|
||||
```mysql
|
||||
select 字段列表 from 表名 [where 条件] group by 分组字段名 [having 分组后过滤条件];
|
||||
```
|
||||
|
||||
*orders表:*
|
||||
|
||||
| customer_id | amount |
|
||||
| ----------- | ------ |
|
||||
| 1 | 100 |
|
||||
| 1 | 200 |
|
||||
| 2 | 150 |
|
||||
| 2 | 300 |
|
||||
|
||||
例如,假设我们有一个名为 `orders` 的表,其中包含 `customer_id` 和 `amount` 列,我们想要计算每个客户的订单总金额,可以这样写查询:
|
||||
|
||||
```text
|
||||
@ -459,8 +534,6 @@ GROUP BY customer_id;
|
||||
|
||||
在这个例子中,`GROUP BY customer_id` 将结果按照 `customer_id` 列的值进行分组,并对每个客户的订单金额求和,生成每个客户的总金额。
|
||||
|
||||
|
||||
|
||||
```text
|
||||
SELECT customer_id, SUM(amount) AS total_amount
|
||||
FROM orders
|
||||
@ -474,10 +547,12 @@ HAVING total_amount > specified_amount;
|
||||
|
||||
**注意事项:**
|
||||
|
||||
• 分组之后,查询的字段一般为聚合函数和分组字段,查询其他字段无任何意义
|
||||
• 分组之后,查询的字段**一般为聚合函数**和分组字段,查询其他字段无任何意义
|
||||
|
||||
• 执行顺序:where > 聚合函数 > having
|
||||
|
||||
|
||||
|
||||
### 排序查询
|
||||
|
||||
语法:
|
||||
@ -496,6 +571,14 @@ order by 字段1 排序方式1 , 字段2 排序方式2 … ;
|
||||
|
||||
- DESC:降序
|
||||
|
||||
```mysql
|
||||
select id, username, password, name, gender, image, job, entrydate, create_time, update_time
|
||||
from tb_emp
|
||||
order by entrydate ASC; -- 按照entrydate字段下的数据进行升序排序
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 分页查询
|
||||
|
||||
```text
|
||||
@ -512,6 +595,8 @@ select 字段列表 from 表名 limit 起始索引, 每页显示记录数
|
||||
|
||||
3. 如果查询的是第一页数据,起始索引可以省略,直接简写为 limit 条数
|
||||
|
||||
|
||||
|
||||
## 多表设计
|
||||
|
||||
### 外键约束
|
||||
@ -520,15 +605,23 @@ select 字段列表 from 表名 limit 起始索引, 每页显示记录数
|
||||
|
||||
```mysql
|
||||
-- 创建表时指定
|
||||
create table 表名(
|
||||
字段名 数据类型,
|
||||
...
|
||||
[constraint] [外键名称] foreign key (外键字段名) references 主表 (主键名)
|
||||
CREATE TABLE child_table (
|
||||
id INT PRIMARY KEY,
|
||||
parent_id INT, -- 外键字段
|
||||
FOREIGN KEY (parent_id)
|
||||
REFERENCES parent_table (id)
|
||||
ON DELETE CASCADE -- 可选,表示父表数据删除时,子表数据也会删除
|
||||
ON UPDATE CASCADE -- 可选,表示父表数据更新时,子表数据会同步更新
|
||||
);
|
||||
|
||||
|
||||
-- 建完表后,添加外键
|
||||
alter table 表名 add constraint 外键名称 foreign key(外键字段名) references 主表(主表列名);
|
||||
ALTER TABLE child_table
|
||||
ADD CONSTRAINT fk_parent_id -- 外键约束的名称,可选
|
||||
FOREIGN KEY (parent_id)
|
||||
REFERENCES parent_table (id)
|
||||
ON DELETE CASCADE
|
||||
ON UPDATE CASCADE;
|
||||
```
|
||||
|
||||
|
||||
@ -537,18 +630,20 @@ alter table 表名 add constraint 外键名称 foreign key(外键字段名)
|
||||
|
||||
|
||||
|
||||
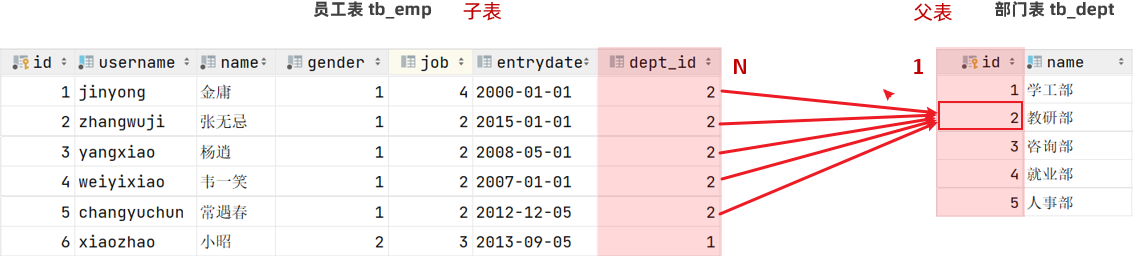
**一对多关系实现:在数据库表中多的一方,添加外键字段,来关联'一'这方的主键。**
|
||||
一对多关系实现:在数据库表中**多的一方**,添加外键字段(如dept_id),来关联'一'这方的主键(id)。
|
||||
|
||||
|
||||
|
||||
### 一对一
|
||||
|
||||
一对一关系表在实际开发中应用起来比较简单,通常是用来做单表的拆分。一对一的应用场景: 用户表=》基本信息表+身份信息表
|
||||
一对一关系表在实际开发中应用起来比较简单,通常是用来做**单表的拆分**。一对一的应用场景: 用户表=》基本信息表+身份信息表,以此来提高数据的操作效率。
|
||||
|
||||

|
||||
|
||||
- 基本信息:用户的ID、姓名、性别、手机号、学历
|
||||
- 身份信息:民族、生日、身份证号、身份证签发机关,身份证的有效期(开始时间、结束时间)
|
||||
|
||||
**一对一 :在任意一方加入外键,关联另外一方的主键,并且设置外键为唯一的(UNIQUE)**
|
||||
一对一 :在**任意一方**加入外键,关联另外一方的主键,并且设置外键为唯一的(UNIQUE)
|
||||
|
||||
|
||||
|
||||
@ -556,11 +651,13 @@ alter table 表名 add constraint 外键名称 foreign key(外键字段名)
|
||||
|
||||
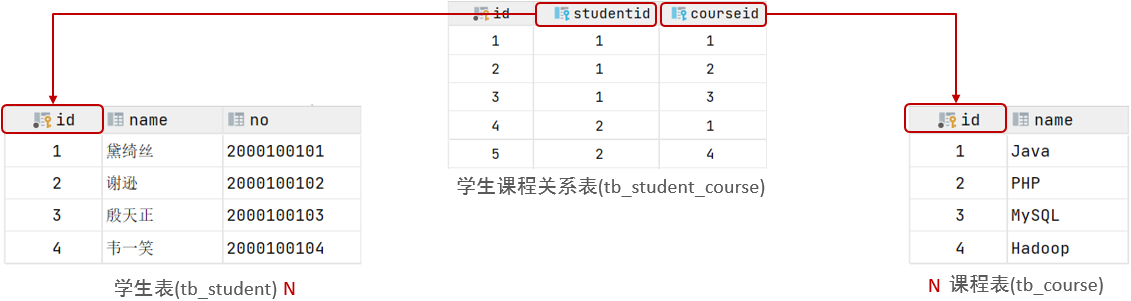
多对多的关系在开发中属于也比较常见的。比如:学生和老师的关系,一个学生可以有多个授课老师,一个授课老师也可以有多个学生。
|
||||
|
||||
|
||||
|
||||
案例:学生与课程的关系
|
||||
|
||||
- 关系:一个学生可以选修多门课程,一门课程也可以供多个学生选择
|
||||
|
||||
- 实现关系:建立第三张中间表(选课表),中间表至少包含两个外键,分别关联两方主键
|
||||
- 实现关系:**建立第三张中间表**(选课表),中间表至少包含两个外键,**分别关联两方主键**
|
||||
|
||||
|
||||
|
||||
@ -572,7 +669,7 @@ alter table 表名 add constraint 外键名称 foreign key(外键字段名)
|
||||
|
||||
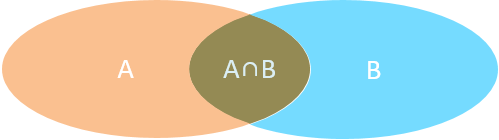
1. 连接查询
|
||||
|
||||
- 内连接:相当于查询A、B交集部分数据
|
||||
- 内连接:相当于查询A、B**交集**部分数据
|
||||
|
||||
|
||||
|
||||
@ -636,16 +733,22 @@ select 字段列表 from 表1 left [ outer ] join 表2 on 连接条件
|
||||
select 字段列表 from 表1 right [ outer ] join 表2 on 连接条件 ... ;
|
||||
```
|
||||
|
||||
> 右外连接相当于查询表2(右表)的**所有**数据,当然也包含表1和表2交集部分的数据。
|
||||
|
||||
|
||||
|
||||
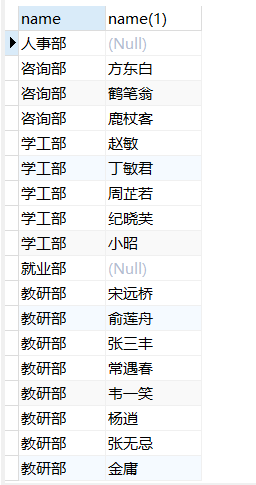
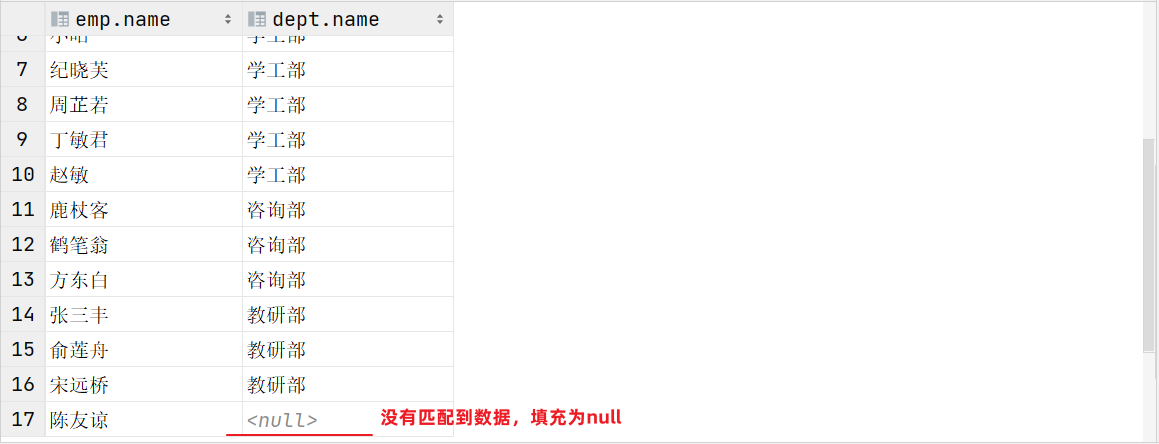
案例:查询部门表中所有部门的名称, 和对应的员工名称
|
||||
|
||||
```text
|
||||
-- 右外连接
|
||||
select dept.name , emp.name
|
||||
from tb_emp AS emp right join tb_dept AS dept
|
||||
-- 左外连接:以left join关键字左边的表为主表,查询主表中所有数据,以及和主表匹配的右边表中的数据
|
||||
select emp.name , dept.name
|
||||
from tb_emp AS emp left join tb_dept AS dept
|
||||
on emp.dept_id = dept.id;
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 子查询
|
||||
|
||||
@ -748,6 +851,8 @@ select * from emp where entrydate > '2006-01-01';
|
||||
select e.*, d.* from (select * from emp where entrydate > '2006-01-01') e left join dept d on e.dept_id = d.id ;
|
||||
~~~
|
||||
|
||||
|
||||
|
||||
## 事务
|
||||
|
||||
简而言之:事务是一组操作的集合,它是一个不可分割的工作单位。事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。
|
||||
@ -757,9 +862,7 @@ select e.*, d.* from (select * from emp where entrydate > '2006-01-01') e left j
|
||||
- 第1种情况:开启事务 => 执行SQL语句 => 成功 => 提交事务
|
||||
- 第2种情况:开启事务 => 执行SQL语句 => 失败 => 回滚事务
|
||||
|
||||
`
|
||||
|
||||
```text
|
||||
```mysql
|
||||
-- 开启事务
|
||||
start transaction ;
|
||||
|
||||
@ -770,8 +873,6 @@ delete from tb_dept where id = 1;
|
||||
delete from tb_emp where dept_id = 1;
|
||||
```
|
||||
|
||||
`
|
||||
|
||||
- 上述的这组SQL语句,如果如果执行成功,则提交事务
|
||||
|
||||
```sql
|
||||
@ -795,6 +896,8 @@ rollback ;
|
||||
|
||||
> 事务的四大特性简称为:ACID
|
||||
|
||||
|
||||
|
||||
## 索引
|
||||
|
||||
索引(index):是帮助数据库高效获取数据的数据结构 。
|
||||
@ -864,8 +967,6 @@ musql默认采用B+树来作索引
|
||||
最大的问题就是在数据量大的情况下,树的层级比较深,会影响检索速度。因为不管是二叉搜索数还是红黑数,一个节点下面只能有两个子节点。此时在数据量大的情况下,就会造成数的高度比较高,树的高度一旦高了,检索速度就会降低。
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
> 说明:如果数据结构是红黑树,那么查询1000万条数据,根据计算树的高度大概是23左右,这样确实比之前的方式快了很多,但是如果高并发访问,那么一个用户有可能需要23次磁盘IO,那么100万用户,那么会造成效率极其低下。所以为了减少红黑树的高度,那么就得增加树的宽度,就是不再像红黑树一样每个节点只能保存一个数据,可以引入另外一种数据结构,一个节点可以保存多个数据,这样宽度就会增加从而降低树的高度。这种数据结构例如BTree就满足。
|
||||
|
||||
下面我们来看看B+Tree(多路平衡搜索树)结构中如何避免这个问题:
|
||||
|
||||
110
自学/力扣Hot 100题.md
110
自学/力扣Hot 100题.md
@ -265,31 +265,40 @@ visited[i][j] = true;
|
||||
|
||||
#### `PriorityQueue`
|
||||
|
||||
- **基于优先堆(最小堆或最大堆)实现**,元素按优先级排序。
|
||||
- **默认是最小堆**,即队首元素是最小的。
|
||||
- **支持自定义排序规则**,通过 `Comparator` 实现。
|
||||
- **常用操作的时间复杂度**:
|
||||
- 基于优先堆(最小堆或最大堆)实现,元素按优先级排序。
|
||||
- **默认是最小堆**,即队首元素是最小的。 `new PriorityQueue<>(Comparator.reverseOrder());`定义最大堆
|
||||
- 支持自定义排序规则,通过 `Comparator` 实现。
|
||||
|
||||
- 插入元素:`O(log n)`
|
||||
- 删除队首元素:`O(log n)`
|
||||
- 查看队首元素:`O(1)`
|
||||
- **常用方法**
|
||||
**常用方法:**
|
||||
|
||||
1. **`add(E e)` / `offer(E e)`**:
|
||||
- 将元素插入队列。
|
||||
- `add` 在队列满时会抛出异常,`offer` 返回 `false`。
|
||||
2. **`remove()` / `poll()`**:
|
||||
- 移除并返回队首元素。
|
||||
- `remove` 在队列为空时会抛出异常,`poll` 返回 `null`。
|
||||
3. **`element()` / `peek()`**:
|
||||
- 查看队首元素,但不移除。
|
||||
- `element` 在队列为空时会抛出异常,`peek` 返回 `null`。
|
||||
4. **`size()`**:
|
||||
- 返回队列中的元素数量。
|
||||
5. **`isEmpty()`**:
|
||||
- 检查队列是否为空。
|
||||
6. **`clear()`**:
|
||||
- 清空队列。
|
||||
`add(E e)` / `offer(E e)`:
|
||||
|
||||
- 功能:将元素插入队列。
|
||||
- 时间复杂度:`O(log n)`
|
||||
- 区别
|
||||
- `add`:当队列满时会抛出异常。
|
||||
- `offer`:当队列满时返回 `false`,不会抛出异常。
|
||||
|
||||
`remove()` / `poll()`:
|
||||
|
||||
- 功能:移除并返回队首元素。
|
||||
- 时间复杂度:`O(log n)`
|
||||
- 区别
|
||||
- `remove`:队列为空时抛出异常。
|
||||
- `poll`:队列为空时返回 `null`。
|
||||
|
||||
`element()` / `peek()`:
|
||||
|
||||
- 功能:查看队首元素,但不移除。
|
||||
- 时间复杂度:`O(1)`
|
||||
- 区别
|
||||
- `element`:队列为空时抛出异常。
|
||||
- `peek`:队列为空时返回 `null`。
|
||||
|
||||
`clear()`:
|
||||
|
||||
- 功能:清空队列。
|
||||
- 时间复杂度:`O(n)`(因为需要删除所有元素)
|
||||
|
||||
```java
|
||||
import java.util.PriorityQueue;
|
||||
@ -303,7 +312,6 @@ public class PriorityQueueExample {
|
||||
// 添加元素
|
||||
minHeap.add(10);
|
||||
minHeap.add(20);
|
||||
minHeap.add(30);
|
||||
minHeap.add(5);
|
||||
|
||||
// 查看队首元素
|
||||
@ -317,7 +325,6 @@ public class PriorityQueueExample {
|
||||
// 输出:
|
||||
// 5
|
||||
// 10
|
||||
// 30
|
||||
// 20
|
||||
|
||||
// 移除队首元素
|
||||
@ -330,11 +337,10 @@ public class PriorityQueueExample {
|
||||
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
|
||||
maxHeap.add(10);
|
||||
maxHeap.add(20);
|
||||
maxHeap.add(30);
|
||||
maxHeap.add(5);
|
||||
|
||||
// 查看队首元素
|
||||
System.out.println("最大堆队首元素: " + maxHeap.peek()); // 输出 30
|
||||
System.out.println("最大堆队首元素: " + maxHeap.peek()); // 输出 20
|
||||
|
||||
// 清空队列
|
||||
minHeap.clear();
|
||||
@ -345,6 +351,51 @@ public class PriorityQueueExample {
|
||||
|
||||
|
||||
|
||||
自己实现大根堆:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int findKthLargest(int[] nums, int k) {
|
||||
int heapSize = nums.length;
|
||||
buildMaxHeap(nums, heapSize);
|
||||
for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
|
||||
swap(nums, 0, i);
|
||||
--heapSize;
|
||||
maxHeapify(nums, 0, heapSize);
|
||||
}
|
||||
return nums[0];
|
||||
}
|
||||
|
||||
public void buildMaxHeap(int[] a, int heapSize) {
|
||||
for (int i = heapSize / 2 - 1; i >= 0; --i) {
|
||||
maxHeapify(a, i, heapSize);
|
||||
}
|
||||
}
|
||||
|
||||
public void maxHeapify(int[] a, int i, int heapSize) {
|
||||
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
|
||||
if (l < heapSize && a[l] > a[largest]) {
|
||||
largest = l;
|
||||
}
|
||||
if (r < heapSize && a[r] > a[largest]) {
|
||||
largest = r;
|
||||
}
|
||||
if (largest != i) {
|
||||
swap(a, i, largest);
|
||||
maxHeapify(a, largest, heapSize);
|
||||
}
|
||||
}
|
||||
|
||||
public void swap(int[] a, int i, int j) {
|
||||
int temp = a[i];
|
||||
a[i] = a[j];
|
||||
a[j] = temp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### **`ArrayList`**
|
||||
|
||||
- 基于数组实现,支持动态扩展。
|
||||
@ -600,11 +651,16 @@ public class QueueExample {
|
||||
|
||||
```java
|
||||
Deque<Integer> stack = new ArrayDeque<>();
|
||||
//Deque<Integer> stack = new LinkedList<>();
|
||||
stack.push(1); // 入栈
|
||||
Integer top1=stack.peek()
|
||||
Integer top = stack.pop(); // 出栈
|
||||
```
|
||||
|
||||
- **LinkedList** 是基于双向链表实现的,每个节点存储数据和指向前后节点的引用。
|
||||
- **ArrayDeque** 则基于动态数组实现,内部使用循环数组来存储数据。
|
||||
- **ArrayDeque** 在大多数情况下性能更好,因为数组在内存中连续,缓存友好,且操作(如 push/pop)开销更小。
|
||||
|
||||
|
||||
|
||||
**双端队列**
|
||||
|
||||
@ -31,6 +31,8 @@
|
||||
| 10 | orders | 订单表 |
|
||||
| 11 | order_detail | 订单明细表 |
|
||||
|
||||
|
||||
|
||||
```java
|
||||
@TableName("user")
|
||||
public class User {
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user