zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Commit on 2025/06/06 周五 19:28:06.29

Browse Source
This commit is contained in:
zhangsan 2025-06-06 19:28:06 +08:00
parent e653d997f0
commit 56cfcca6e1
13 changed files with 1117 additions and 299 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

314
科研/ZY网络重构分析.md
View File

@ -393,9 +393,9 @@ $$
### **非0/1矩阵** ## **非0/1矩阵**
#### **量化误差** ### **量化误差**
对估计矩阵 $\tilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类，得到每个簇中心 $\{c_k\}_{k=1}^K$。 对估计矩阵 $\tilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类，得到每个簇中心 $\{c_k\}_{k=1}^K$。
@ -412,7 +412,7 @@ $$
#### 对于归一化向量 $x_m$ 的研究 ### 对于归一化向量 $x_m$ 的研究
$$ $$
x_m = \begin{bmatrix} x_{m,1} \\ x_{m,2} \\ \vdots \\ x_{m,d} \end{bmatrix} x_m = \begin{bmatrix} x_{m,1} \\ x_{m,2} \\ \vdots \\ x_{m,d} \end{bmatrix}
@ -460,7 +460,7 @@ $$
#### 带权重构需控制两类误差： ### 带权重构需控制两类误差：
这里暂时忽略特征向量的扰动，即 $x_m=\widetilde x_m$ 这里暂时忽略特征向量的扰动，即 $x_m=\widetilde x_m$
@ -473,11 +473,11 @@ $$
- 设矩阵 $A$ 的秩为 $r$ - 设矩阵 $A$ 的秩为 $r$
$$ $$
A - \widetilde A=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T. A - \tilde A=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \tilde\lambda_m\,\tilde x_m\tilde x_m^T=\sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
$$ $$
$$ $$
\Bigl\|\sum_{m=1}^r \Delta\lambda_m\, x_m x_m^T\Bigr\|_F = \sqrt{\sum_{m=1}^r (\Delta\lambda_m)^2}. \eta_F=\Bigl\|\sum_{m=1}^r \Delta\lambda_m\, x_m x_m^T\Bigr\|_F = \sqrt{\sum_{m=1}^r (\Delta\lambda_m)^2}.
$$ $$
​ ​
@ -503,7 +503,7 @@ $$
3. **总的误差** 3. **总的误差**
$$ $$
\text{误差矩阵： } A - A_\kappa = \left( A - \widetilde{A} \right) + \left( \widetilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \text{误差矩阵： } A - A_\kappa = \left( A - \tilde{A} \right) + \left( \tilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \tilde{\lambda}_m x_m x_m^T
$$ $$
- 研究单个元素误差： - 研究单个元素误差：
$$ $$
@ -533,16 +533,30 @@ $$
4. **最终约束条件**： 4. **最终约束条件**：
$$ $$
|(A - A_\kappa)_{ij}| \leq 量化阈值\tau |(A - A_\kappa)_{ij}| \leq 容忍误差\tau
$$ $$
$$ $$
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 容忍误差\tau
$$ $$
#### 量化阈值推导
$$
\delta_F
= \lVert A - A_k \rVert_F
= \sqrt{\sum_{i,j} \bigl(A - A_k\bigr)_{ij}^{2}}
\;\le\; \sqrt{N^{2}\,\tau^{2}}
\;=\; N\tau
$$
### 容忍误差推导
#### **容忍误差**
要保证重构矩阵 $A_\kappa$ 在每个位置上“落到”正确的某一 簇而不搞混，就必须让重构误差的最大绝对值严格小于任意两个相邻量化级别之间的半距（half‐spacing）。具体地： 要保证重构矩阵 $A_\kappa$ 在每个位置上“落到”正确的某一 簇而不搞混，就必须让重构误差的最大绝对值严格小于任意两个相邻量化级别之间的半距（half‐spacing）。具体地：
@ -562,23 +576,224 @@ $$
d_{\min} = \min_{1\le m\le K-1} d_m. d_{\min} = \min_{1\le m\le K-1} d_m.
$$ $$
3. **通用误差阈值** 3. **通用容忍误差**
为确保重构值不会"越界"到相邻级别，取阈值： 为确保重构值不会"越界"到相邻级别，取阈值：
$$ $$
\boxed{\tau = \frac{d_{\min}}{2}.} \boxed{\tau = \frac{d_{\min}}{2}.}
$$ $$
量化误差和数据的分布（不是重构出来的矩阵值）有关，和容忍误差无关。
**示例：** **示例：**
1. 0-1矩阵，$a=0, b=1,K=2$，量化阈值为0.5。 1. 0-1矩阵，$a=0, b=1,K=2$，容忍误差为0.5。
2. 量化级别 $\{0,\,0.3,\,0.7,\,1\}$ ，$K=4$ 时： 2. 量化级别 $\{0,\,0.3,\,0.7,\,1\}$ ，$K=4$ 时：
- 相邻间距：$0.3, 0.4, 0.3$ - 相邻间距：$0.3, 0.4, 0.3$
- $d_{\min}=0.3$，故 $\tau=0.15$ - $d_{\min}=0.3$，故 $\tau=0.15$
#### 维数选择推导 #### **量化误差**
量化阈值：重构矩阵与真实矩阵的对应元素误差最大值为 $\tau$ ；
量化误差：真实矩阵与经量化之后的对应元素误差最大值为 $\delta$
当我们把一个数值 $x$ 量化到某个中心 $v_m$ 时，它本身就会产生一个"量化误差"：
$$
\underbrace{|x - v_m|}_{\text{量化误差}}.
$$
**1.当 $x$ 落在第 $m$ 个区间时**
假设某个实数 $x$ 满足
$$ t_{m-1} \leq x < t_{m} $$
(其中我们约定 $t_{0} = -\infty$, $t_{K} = +\infty$)，这时把 $x$ 量化到中心 $v_{m}$。
**2.计算量化误差**
由于 $t_{m} = \frac{v_{m} + v_{m+1}}{2}$ 且 $t_{m-1} = \frac{v_{m-1} + v_{m}}{2}$，当 $x \in [t_{m-1}, t_{m})$ 时，离它所在的中心 $v_{m}$ 的最大距离，就是它正好位于这段区间的"最远端"——也就是：
$$
\max_{x \in [t_{m-1}, t_{m})} |x - v_{m}| = \max \left\{ |t_{m-1} - v_{m}|, |t_{m} - v_{m}| \right\}.
$$
但 $t_{m} - v_{m} = \frac{v_{m+1} - v_{m}}{2} = \frac{d_{m}}{2}$，
同理 $v_{m} - t_{m-1} = \frac{v_{m} - v_{m-1}}{2} = \frac{d_{m-1}}{2}$。
所以对任意落在第 $m$ 个决策区间里的 $x$，其量化到 $v_{m}$ 时的偏差至多为
$$
|x - v_{m}| \leq \max \left( \frac{d_{m-1}}{2}, \frac{d_{m}}{2} \right) \leq \frac{d_{\min}}{2}.
$$
综上，对所有可能的 $x$：
$$
\max_{x} |x - Q(x)| = \frac{d_{\min}}{2}.
$$
于是定义 $\delta = \frac{d_{\min}}{2}$
### 已知量化误差推导容忍误差和码本
![6.6](https://pic.bitday.top/i/2025/06/06/lovsvp-0.png)
#### **推导容忍误差**
已知：所有待量化的数都落在 $[X_{\min}, X_{\max}]$
：量化误差上限
$$
\delta = \max_{x} |x - Q(x)|.
$$
1.因为对所有落在第 $m$ 个区间的点，都有
$$
|x - v_{m}| \leq \delta
$$
由"落在第 $m$ 区间"可推出
$$
|x - v_{m}| \leq \max \left\{\frac{v_{m+1} - v_{m}}{2}, \frac{v_{m} - v_{m-1}}{2}\right\} \leq \delta.
$$
因此
$$
\frac{v_{m+1} - v_{m}}{2} \geq \delta, \quad \frac{v_{m} - v_{m-1}}{2} \geq \delta, \quad \forall m.
$$
2.这意味着"任意相邻中心间距"都不小于 $2\delta$，即
$$
v_{m+1} - v_{m} \geq 2 \delta, \quad \forall m \implies d_{\min} = 2 \delta.
$$
3."容忍阈值"定义为使得重构值 $\widehat{x}$ 与真实中心 $v_{m}$ 之间只要偏差在 $\tau$ 以内，量化就不会跳到旁边。显然
$$
\tau = \min_{m}\left\{\frac{v_{m+1} - v_{m}}{2}\right\} = \frac{d_{\min}}{2} = \frac{2 \delta}{2} = \delta.
$$
#### **构造码本：**
**1.确定量化间隔**
因为"量化误差的最大值"为 $\delta$，在一维的均匀量化里相邻两个中心（码本）中点到中心的距离就是量化误差的上界，所以我们令
$$
\Delta = 2\,\delta.
$$
相邻两个量化中心之间的距离都取 $\Delta$，这样任何一个点到它最近中心的距离最多是 $\tfrac{\Delta}{2} = \delta$。
**2.确定量化级别数 $K$**
为了覆盖整个区间 $[X_{\min},\,X_{\max}]$，这些间隔为 $\Delta=2\delta$ 的"窗口"要铺下去。具体来说，如果我们有 $K$ 个中心 $\{v_1,\dots,v_K\}$，并且它们相邻之间都相差 $\Delta$，那么最左边中心的"覆盖下限"是
$$
v_1 - \delta = v_1 - \tfrac{\Delta}{2},
$$
最右边中心的"覆盖上限"是
$$
v_K + \delta = v_K + \tfrac{\Delta}{2}.
$$
要保证所有 $x \in [X_{\min},\,X_{\max}]$ 都能落进这串"区间并覆盖"，只要
$$
v_1 - \tfrac{\Delta}{2} \le X_{\min}, \quad v_K + \tfrac{\Delta}{2} \ge X_{\max}.
$$
下面我们令最左侧的中心刚好满足 $v_1 - \tfrac{\Delta}{2} = X_{\min}$，于是
$$
v_1 = X_{\min} + \frac{\Delta}{2} = X_{\min} + \delta.
$$
如果相邻中心间距都为 $\Delta$，那么第 $m$ 个中心就是
$$
v_m = v_1 + (m-1)\,\Delta = \bigl(X_{\min} + \delta\bigr) + (m-1)\cdot(2\delta).
$$
此时，第 $K$ 个中心为
$$
v_K = X_{\min} + \delta + (K-1)\,2\delta = X_{\min} + (2K - 1)\,\delta.
$$
要满足"第 $K$ 个中心加上 $\delta$ 能覆盖到 $X_{\max}$"，即
$$
v_K + \delta = X_{\min} + (2K - 1)\,\delta + \delta = X_{\min} + 2K\,\delta \ge X_{\max}.
$$
因此
$$
2\,K\,\delta \ge X_{\max} - X_{\min} \Longleftrightarrow K \ge \frac{X_{\max} - X_{\min}}{2\,\delta}.
$$
我们取最小的整数满足这个不等式：
$$
\boxed{K = \Bigl\lceil \frac{X_{\max} - X_{\min}}{2\,\delta} \Bigr\rceil.}
$$
**3.得到码本 $\{v_m\}$ 和阈值**
1. 令
$$
\Delta = 2\,\delta,\quad K = \Bigl\lceil \tfrac{X_{\max} - X_{\min}}{\Delta} \Bigr\rceil.
$$
2. 对 $m = 1,2,\dots,K$，令
$$
v_m = X_{\min} + \delta + (m - 1)\,\Delta = X_{\min} + \delta + (m - 1)\,(2\,\delta) = X_{\min} + \bigl(2m - 1\bigr)\,\delta.
$$
- 此时，第 1 个中心是 $v_1 = X_{\min} + \delta$；
- 第 $K$ 个中心是 $v_K = X_{\min} + (2K - 1)\,\delta$。
3. 中点阈值数组 $\{\,t_m\mid m=1,\dots,K-1\}$ 就是
$$
t_m = \frac{v_m + v_{m+1}}{2} = \frac{\bigl[X_{\min} + (2m-1)\delta\bigr] + \bigl[X_{\min} + (2(m+1)-1)\delta\bigr]}{2} = X_{\min} + 2m\,\delta.
$$
因此，决策规则是：
- 如果 $x < t_1 = X_{\min} + 2\delta$，就量化到 $v_1 = X_{\min} + \delta$；
- 如果 $t_{m-1} \le x < t_m$ (即 $X_{\min} + 2(m-1)\delta \le x < X_{\min} + 2m\delta$)，就量化到
$$
v_m = X_{\min} + (2m-1)\,\delta;
$$
- 如果 $x \ge t_{K-1} = X_{\min} + 2(K-1)\delta$，就量化到
$$
v_K = X_{\min} + (2K-1)\,\delta.
$$
### 维数选择推导
$$ $$
\frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau \frac{1}{2}\left(\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\right)\leq 量化阈值\tau
@ -643,6 +858,79 @@ while low < high:
### 最近邻量化
算法思想：
1. **已知量化级别**
先假定你已有 $K$ 个量化级别（或簇中心）：
$$ v_1 < v_2 < \cdots < v_K $$
这些值通常是事先人为设定好的、或者某种优化后得到的最佳码本。
2. **计算决策边界（中点阈值）**
对于一维空间，相邻两个量化级别之间的“分界”很自然就是它们的中点：
$$ t_m = \frac{v_m + v_{m+1}}{2}, \quad m = 1,\dots,K-1 $$
也就是一旦输入 $x$ 落在 $[t_{m-1},\,t_m)$ 这个区间（约定 $t_0 = -\infty$，$t_K = +\infty$），就映为 $v_m$。
3. **最近邻映射**
对于矩阵 $M$ 中的每个元素 $x = M_{ij}$，只要找到它对应的区间号 $m$，就把 $x$ 替换为 $v_m$。
由于阈值已经按增序排列，查找时可以用二分搜索（binary search），使得整体复杂度为 $O(\log K)$／次映射。
4. **误差保证**
为了确保“重构误差”不会把重构值落到相邻簇去，需要保证真实误差 $\lvert A_{\kappa}(i,j) - M_{ij} \rvert$ 严格小于任意两个相邻量化级别之间的半距 $\frac{d_{\min}}{2}$。
这里 $d_m = v_{m+1} - v_m$，取最小间距 $d_{\min} = \min_{m} d_m$，就有误差阈值 $\tau = \frac{d_{\min}}{2}$。
```text
输入：数组 v[1..K]（升序排列）
输出：阈值数组 t[1..(K-1)]（对应各区间的分界）
function initialize_thresholds(v[1..K]):
for m = 1 to K-1 do
t[m] = ( v[m] + v[m+1] ) / 2
end for
return t # 长度为 K-1
输入：矩阵 M (尺寸 N×N)，量化级别 v[1..K]，阈值数组 t[1..(K-1)]
输出：量化后矩阵 Ḿ（N×N）
function quantizeMatrix(M, v, t):
let N = number_of_rows(M) # 假设 M 是正方阵 N×N
创建新矩阵 Ḿ，大きさ N×N
for i = 1 to N do
for j = 1 to N do
x = M[i][j]
# 在阈值数组 t 中二分查找，找到第一个 t[m] 使得 x < t[m]
# 如果没有找到（即 x >= t[K-1]），则归到最后一个簇
idx = binarySearchThreshold(t, x)
# binarySearchThreshold 的返回：
# 如果 x < t[1]，返回 idx = 1；
# 如果 t[m-1] <= x < t[m]，返回 idx = m；
# 如果 x >= t[K-1]，返回 idx = K。
Ḿ[i][j] = v[idx]
end for
end for
return Ḿ
```
如果量化阈值不一样，你需要**预先**知道矩阵的某个元素$|(A - A_\kappa)_{ij}|$的真实值属于哪个类别（1、4、10），以给元素误差不同的量化阈值，而不是默认的 $d_{\min}$ 如果量化阈值不一样，你需要**预先**知道矩阵的某个元素$|(A - A_\kappa)_{ij}|$的真实值属于哪个类别（1、4、10），以给元素误差不同的量化阈值，而不是默认的 $d_{\min}$

113
科研/草稿.md
View File

@ -1,91 +1,52 @@
Here’s the revised content with formulas wrapped in `$` or `$$` for Markdown compatibility: **肯定有，而且一旦你能在分布式/隐私受限场景下拿到「全局网络的谱参数」（如 Laplacian / Adjacency 矩阵的特征值、特征向量或奇异值），在三条研究线上都能直接落地：**
--- ------
### **步骤 1：验证矩阵对称性** ## 1 联邦学习（FL）
确保 $A$ 是实对称矩阵（即 $A = A^\top$），此时SVD可通过特征分解直接构造。
--- | 用途 | 关键想法 | 为什么谱信息有用 |
| ------------------------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
| **① 自适应通信与收敛分析** | 用全局**谱隙 (λ₂)** 来动态调节局部迭代步长、通信轮次或拓扑重连 | 谱隙越大、网络混合越快→理论与实验证明可显著提升去中心化 SGD/FedAvg 的收敛速率 citeturn0search0turn0search6 |
| **② 客户端谱聚类 / 个性化联邦** | 先用特征向量做**谱嵌入**→聚类→组内共享模型、组间异步 | 典型工作 FedSpectral / FedSpectral⁺ 把全局谱计算移到服务器侧，在保护隐私的同时得到近乎中心化的聚类质量，进而加速收敛、降低异质性影响 citeturn0search1turn0search4 |
| **③ 谱正则化的模型聚合** | 把全局 Laplacian 引入损失或梯度校正项（Graph-FedAvg/FedGCN 思路） | 让跨客户端的“邻边”显式参与参数更新，可保留跨域关联信息，减少过拟合 citeturn0search3 |
| **④ 通信压缩 / 子空间同步** | 只同步低频（低阶特征向量）系数，忽略高频噪声 | 保持主要结构信息同时大幅减通信量；已在分布式 PCA、图信号处理里验证可行 |
### **步骤 2：计算特征分解** ------
对 $A$ 进行特征分解：
$$
A = Q \Lambda Q^\top
$$
其中：
- $Q$ 是正交矩阵（$Q^\top Q = I$），列向量为 $A$ 的特征向量。
- $\Lambda = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$，$\lambda_i$ 为 $A$ 的特征值（可能有正、负或零）。
--- ## 2 联邦蒸馏（含模型蒸馏 & 数据蒸馏）
### **步骤 3：构造奇异值矩阵 $\Sigma$** | 场景 | 谱参数的切入点 | 预期收益 |
- **奇异值**：取特征值的绝对值 $\sigma_i = |\lambda_i|$，得到对角矩阵： | ------------------------ | ------------------------------------------------------------ | ---------------------------------------------- |
$$ | **教师权重自适应** | 以节点中心性或谱嵌入距离为权重，给“信息量大”的客户端更高蒸馏系数 | 提升学生模型收敛速度与公平性 |
\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_n) | **知识子空间蒸馏** | 仅在**低频谱子空间**聚合 logits / representations | 去噪声、避免隐私泄漏（高频往往包含可识别细节） |
$$ | **跨客户端软标签一致性** | 在谱域里做对齐损失（例如 KL or MSE on Laplacian-filtered logits） | 比直接对齐原始输出更稳健，抗异构数据分布 |
- **排列顺序**：通常按 $\sigma_i$ 降序排列（可选，但推荐）。
--- ------
### **步骤 4：处理符号（负特征值）** ## 3 强化学习（RL / MARL）
- **符号矩阵 $S$**：定义对角矩阵 $S = \text{diag}(s_1, s_2, \dots, s_n)$，其中：
$$
s_i = \begin{cases}
1 & \text{if } \lambda_i \geq 0, \\
-1 & \text{if } \lambda_i < 0.
\end{cases}
$$
- **左奇异向量矩阵 $U$**：调整特征向量的方向：
$$
U = Q S
$$
即 $U$ 的列为 $Q$ 的列乘以对应特征值的符号。
--- | 应用类别 | 机制 | 谱信息带来的好处 |
| -------------------------------------------- | ------------------------------------------------ | -------------------------------------------------------- |
| **多智能体共识策略梯度** | 利用谱隙设计**共识速率**或自适应邻域 | 谱隙大→梯度共识快→更稳健收敛 citeturn0search2 |
| **图拉普拉斯基表示 / Proto-Value Functions** | 把 Laplacian 特征向量作为状态特征或 value 基函数 | 改善探索、加速值逼近；在图状/离散大状态空间尤其有效 |
| **信用分配与奖励塑形** | 根据节点中心性或谱分量对局部奖励重加权 | 避免“边缘”智能体被忽略，提升团队协作效率 |
| **谱驱动的通信拓扑优化** | 用全局谱优化连边（如增大 λ₂、降低最大度） | 在保持低通信成本的同时最小化非平稳性 citeturn0search5 |
### **步骤 5：确定右奇异向量矩阵 $V$** ------
由于 $A$ 对称，右奇异向量矩阵 $V$ 直接取特征向量矩阵：
$$
V = Q
$$
--- ## 4 研究落点与可行实现
### **步骤 6：组合得到SVD** 1. 集中式谱估计 + 去中心化应用
最终SVD形式为： - 服务器用一次安全多方计算 (SMPC) 或差分隐私聚合奇异值 → 客户端只需取回少量谱系数。
$$ 2. 在线谱跟踪
A = U \Sigma V^\top - 在训练过程中增量维护前 k 个特征向量，配合 FL 训练轮同步。
$$ 3. 谱-aware 自适应调度器
验证： - 把 λ₂、节点特征向量 norm 等指标作为调度信号（何时重连、何时蒸馏）。
$$ 4. 跨领域验证
U \Sigma V^\top = (Q S) \Sigma Q^\top = Q (S \Sigma) Q^\top = Q \Lambda Q^\top = A - **医疗影像 FL**：用谱聚类把医院分群；**车联网 RL**：用谱隙调整车-路协同频率；**隐私推荐**：用低频谱蒸馏稳定用户兴趣漂移。
$$
（因为 $S \Sigma = \Lambda$，例如 $\text{diag}(-1) \cdot \text{diag}(2) = \text{diag}(-2)$）。
--- ------
### **关键性质与注意事项** ### 一句话结论
1. **奇异值与特征值**：$\Sigma$ 的非零对角元是 $|\Lambda|$ 的非零对角元。
2. **零特征值**：若 $\lambda_i = 0$，则 $\sigma_i = 0$，对应 $U$ 和 $V$ 的列向量属于 $A$ 的核空间。
3. **唯一性**：
- 奇异值 $\Sigma$ 唯一（按降序排列时）。
- 奇异向量 $U$ 和 $V$ 的符号可能不唯一（因特征向量方向可反转）。
4. **计算效率**：对称矩阵的SVD无需计算 $AA^\top$ 或 $A^\top A$，直接通过特征分解获得。
--- > **只要能掌握全局谱参数，你就能在 FL、联邦蒸馏和强化学习里**——调速收敛、做隐私友好的聚类、设计更稳健的蒸馏权重，以及加速多智能体共识 —— **这些都是现有文献已验证或正快速演化的活跃方向**。把谱信息当作“全局结构先验”，可以显著提升分布式学习系统的效率与鲁棒性。
### **示例**
设对称矩阵 $A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$：
1. **特征分解**：
- 特征值：$\lambda_1 = 1$, $\lambda_2 = -1$。
- 特征向量：$Q = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$。
2. **构造SVD**：
- $\Sigma = \text{diag}(1, 1)$（$|\lambda_i|$）。
- $S = \text{diag}(1, -1)$，故 $U = Q S = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}$。
- $V = Q$。
3. **结果**：
$$
A = \underbrace{\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}}_U \underbrace{\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}}_\Sigma \underbrace{\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}^\top}_{V^\top}
$$
---

170
科研/郭款论文.md
View File

@ -527,9 +527,9 @@ $$
**矩阵重构算法步骤为：** **矩阵重构算法步骤为：**
1. **输入** 由卡尔曼滤波预测得来！ 1. **输入**
- 预测特征向量矩阵 $X \in \mathbb{R}^{n \times r}$ - 特征向量矩阵 $X \in \mathbb{R}^{n \times r}$
- 特征值矩阵 $\Lambda \in \mathbb{R}^{r \times r}$ - 特征值矩阵 $\Lambda \in \mathbb{R}^{r \times r}$
2. **初始化** 2. **初始化**
@ -566,125 +566,139 @@ $$
**例：假设我们有一个 $2 \times 2$ 对称非负矩阵**
**例：假设我们有一个 $3 \times 3$ 对称非负矩阵**
$$ $$
A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}. A=\begin{bmatrix}
4 & 2 & 1\\
2 & 3 & 2\\
1 & 2 & 3
\end{bmatrix}
\qquad(\text{显然 }A=A^{\mathsf T},\;A_{ij}\ge 0)
$$ $$
--- ---
**1. 初始步骤：构造 $B$ 和 $Q$** **1. 初始步骤：构造 $B$ 和 $Q$**
首先*对 $A$ 做谱分解*，*或者卡尔曼滤波预测*得到（已知结果）： 首先*对 $A$ 做谱分解*，*或者卡尔曼滤波预测*得到（已知结果）,：
- 特征值：$\lambda_1=4, \lambda_2=2$
- 对应的单位特征向量：
$$ $$
x_1 = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix}, \quad A=X\Lambda X^{\mathsf T},\quad
x_2 = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{pmatrix}. \Lambda=\operatorname{diag}(6.7136,\;2.5171,\;0.7693)
$$ $$
构造
$$ $$
X = \begin{bmatrix} x_1 & x_2 \end{bmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}, \quad X=
\Lambda = \begin{pmatrix} 4 & 0 \\ 0 & 2 \end{pmatrix}. \begin{bmatrix}
-0.6265 & -0.7166 & 0.3065\\
-0.6032 & 0.1968 & -0.7729\\
-0.4936 & 0.6691 & 0.5556
\end{bmatrix}
$$ $$
取 $r=2$（通常𝑟 ≪ $n$，这里仅作例子），定义 假设只保留最大的两条特征线
$$ $$
B = X \Lambda^{\frac{1}{2}} \quad \text{其中} \quad \Lambda^{\frac{1}{2}} = \begin{pmatrix} 2 & 0 \\ 0 & \sqrt{2} \end{pmatrix}. X_r=
\begin{bmatrix}
-0.6265 & -0.7166\\
-0.6032 & 0.1968\\
-0.4936 & 0.6691
\end{bmatrix},
\qquad
\Lambda_r=\operatorname{diag}(6.7136,\;2.5171)
$$ $$
因此，
$$ $$
B = X \Lambda^{\frac{1}{2}} = B=X_r\Lambda_r^{1/2} =
\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{bmatrix}
\begin{pmatrix} 2 & 0 \\ 0 & \sqrt{2} \end{pmatrix} -1.6233 & -1.1370\\
= \begin{pmatrix} \frac{2}{\sqrt{2}} & \frac{\sqrt{2}}{\sqrt{2}} \\ \frac{2}{\sqrt{2}} & -\frac{\sqrt{2}}{\sqrt{2}} \end{pmatrix} -1.5630 & \;\;0.3122\\
= \begin{pmatrix} \sqrt{2} & 1 \\ \sqrt{2} & -1 \end{pmatrix}. -1.2789 & \;\;1.0616
\end{bmatrix}
$$ $$
同时，初始令 $Q = I_2$（$2 \times 2$ 单位矩阵）。
--- ---
**2. 初始 $U$ 的计算** **2.rEVD 迭代（示范 $0 \to 1 \to \dots \to 9$ 步）**
按照迭代初始公式： | 迭代 | $Q^{(k)}$（$2 \times 2$） | $U^{(k)}=\max(0,BQ^{(k)})$（列举主要行） | 误差 $\lVert U^{\mathsf T}(U-BQ)\rVert_F^2$ |
$$ | ---- | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------- |
U \approx \max\Bigl(0, B Q \Bigr). | 0 | $I$ | $\begin{bmatrix}0&0\\0&0.3122\\0&1.0616\end{bmatrix}$ | 3.4063 |
$$ | 1 | $\begin{bmatrix}\;0.5528&-0.8333\\0.8333&0.5528\end{bmatrix}$ | $\begin{bmatrix}0&0.7241\\0&1.4750\\0.1776&1.6526\end{bmatrix}$ | 4.9581 |
由于 $Q = I_2$，初始 $U$ 就是 | 2 | … | … | 3.8632 |
$$ | ··· | … | … | … |
U^{(0)} = \max\Bigl(0, B \Bigr) = \max\left(0, \begin{pmatrix} \sqrt{2} & 1 \\ \sqrt{2} & -1 \end{pmatrix}\right) | 9 | — | $\begin{bmatrix}0&1.9814\\1.1283&1.1258\\1.5933&0.4731\end{bmatrix}$ | **0.0072** |
= \begin{pmatrix} \sqrt{2} & 1 \\ \sqrt{2} & 0 \end{pmatrix}.
$$ > 每一轮都先
> $F=U^{\mathsf T}B\stackrel{\text{svd}}{=}\!H\Sigma V^{\mathsf T},\;Q=VH^{\mathsf T}$，
> 再 $U=\max(0,BQ)$。
> 到第 9 步误差已降到 $7\times10^{-3}$，继续几步即可达到更小容差。
--- ---
**3. 更新 $Q$ 的步骤** **3.最终非负矩阵 $U$ 及重构**
$$
U=\!
\begin{bmatrix}
0.0000 & 1.9814\\
1.1283 & 1.1258\\
1.5933 & 0.4731
\end{bmatrix},
\qquad
A' = UU^{\mathsf T}=
\begin{bmatrix}
3.9259 & 2.2307 & 0.9374\\
2.2307 & 2.5404 & 2.3303\\
0.9374 & 2.3303 & 2.7626
\end{bmatrix}
$$
原矩阵 $A$ 的差：
接下来计算中间矩阵
$$ $$
F = U^{(0)T} B. A-A'=
$$ \begin{bmatrix}
计算 $U^{(0)T}$： \;0.0741 & -0.2307 & 0.0626\\
$$ -0.2307 & \;0.4596 & -0.3303\\
U^{(0)T} = \begin{pmatrix} \sqrt{2} & \sqrt{2} \\ 1 & 0 \end{pmatrix}. \;0.0626 & -0.3303 & 0.2374
$$ \end{bmatrix}
因此，
$$
F = U^{(0)T} B = \begin{pmatrix} \sqrt{2} & \sqrt{2} \\ 1 & 0 \end{pmatrix} \begin{pmatrix} \sqrt{2} & 1 \\ \sqrt{2} & -1 \end{pmatrix}= \begin{pmatrix} 4 & 0 \\ \sqrt{2} & 1 \end{pmatrix}.
$$
接下来，对 $F$ 进行奇异值分解（SVD）：设
$$
F = H \Sigma V^T.
$$
（在实际数值计算中可以得到具体 $H, \Sigma, V$；此处我们只说明流程。）
然后按照更新公式，令
$$
Q \leftarrow V H^T.
$$ $$
这一步的作用是“旋转” $B$ 的基，使得 $U$ 更贴近满足 $A \approx U U^T$ 的目标。 已处于可接受的近似误差范围，并且 **$U$ 与 $A'$ 均为非负**，即可直接用于后续的 SNMF-based 网络嵌入或聚类量化。
---
**4. 迭代更新 $U$**
在更新了 $Q$ 后，再更新 $U$ 的公式仍为： #### 重构误差分析
初始传入的**r个特征对**，这个r很关键。
| 参数 | 决定了什么 | 会发生什么事 |
| ------------------------------ | -------------------------------------- | ------------------------------------------ |
| **$r$（截断阶数 / 嵌入维度）** | 你允许模型用多少自由度来"拟合"原始矩阵 | 先天上把可达到的最小误差卡死在一个**下界** |
- **截断误差（不可避免）**
只保留前 $r$ 条特征线以后，任何再聪明的算法都只能在这 **$r$ 维子空间** 里折腾；
理论上最好的也就是
$$ $$
U \leftarrow \max\bigl(0, B Q \bigr). \|A - X_r\Lambda_rX_r^{\!\top}\|_F^2 \;=\; \sum_{i=r+1}^{n}\lambda_i^2,
$$ $$
也就是说，用新的 $Q$ 重新计算 $B Q$，再将负值截断为零。
然后再重复“计算 $F = U^T B$ → SVD 得到新 $Q$ → 更新 $U$”这一过程，直至满足收敛条件（例如 $\|U^T(U - B Q)\|_F^2 \le \varepsilon$）。 也就是把后面没选的特征值的平方加起来。
$r$ 选小了，这个和就大——这是 **谱截断误差**，跟迭代多少次无关。
--- - **优化误差（可迭代消除）**
rEVD / SNMF 的迭代只是想在"既保持 $\text{rank} \leq r$, 又非负"这两个约束里，把误差降到 **谱截断极限之上最小**。
迭代越多，这一部分误差会指数式衰减到机器精度；但它永远不可能穿透前面的"墙"。
**5. 迭代结束后的意义** > **一句话**：迭代能消掉"姿势不对"的误差，却消不掉"维度不够"的误差。
当迭代停止时，得到的 $U$ 满足
$$
A \approx U U^T.
$$
此时 $U$（尺寸为 $2 \times 2$ 的矩阵）就是对 $A$ 进行低维嵌入得到的“特征表示”，它不仅满足非负性，而且通过内积 $U U^T$ 能近似重构出原矩阵 $A$。
#### 疑问 #### 疑问
郭和颜的论文都说满足低秩或者具有低秩性条件的矩阵，SNMF分解出的矩阵是唯一的。可能指的是经过特定算法，输入固定，输出也是固定的。 **！！！为什么采用SNMF?** 5.13日我的思考：卡尔曼滤波得到的特征值和特征向量存在噪声 直接进行谱分解重构会导致重构出来的矩阵不满足对称性。但是SNMF在迭代的过程中增加了**非负**且**对称**的约束！并且得到的U是个低维的，你可以仅在需要的时候进行重构，其他时候就保留U就行！！！
但是：
- **旋转自由度**：若 $(U, U^T)$ 是一个解，则对任意正交矩阵 $R$（满足 $RR^T=I$），$(UR, R^TU^T)$ 也是有效解。
！！！为什么采用SNMF? 5.13日我的思考：卡尔曼滤波得到的特征值和特征向量存在噪声 直接进行谱分解重构会导致重构出来的矩阵不满足对称性。但是SNMF在迭代的过程中增加了非负且对称的约束！并且得到的U是个低维的，你可以仅在需要的时候进行重构，其他时候就保留U就行！！！

191
科研/高飞论文.md
View File

@ -275,9 +275,90 @@ $$
## 特征值精度预估 ## 特征值精度预估
卡尔曼滤波的状态更新方程为 $x_k' = x_k + K (z_k - H x_k)$，如果增益系数 $K$ 变小，那么先验预测 $x_k$ 接近真实值；反之如果增益系数 $K$ 变大，则测量值 $z_k$ 更接近真实值。增益系数$K$受到过程噪声$Q$以及观测噪声$R$的影响，因此估算的过程噪声$Q$和观测噪声$R$，与实际值是否一致，将决定$K$是否准确，从而影响滤波的精度。 ### 1. 噪声随机变量与协方差
设过程噪声$Q$的期望为$\mu_q$，方差为$\sigma_q$；观测噪声$R$的期望为$\mu_r$，方差为$\sigma_r$。其中$\mu_q$、$\sigma_q$和$\mu_r$、$\sigma_r$时未知；$n_q$、$n_r$分别为过程噪声与观测噪声的采样长度。 | 符号 | 含义 |
| ----- | ------------------------------------ |
| $w_i$ | 第 $i$ 个**过程噪声**样本 |
| $v_j$ | 第 $j$ 个**观测噪声**样本 |
| $Q$ | 过程噪声的真实方差（协方差矩阵退化） |
| $R$ | 观测噪声的真实方差（协方差矩阵退化） |
> **说明**：
>
> - 在矩阵形式的 Kalman Filter 中，通常写作
> $$
> w_k\sim\mathcal N(0,Q),\quad v_k\sim\mathcal N(0,R).
> $$
>
> - 这里为做统计检验，把 $w_i, v_j$ 当作样本，$Q,R$ 就是它们在**标量**情况下的方差。
---
### 2. 样本统计量
| 符号 | 含义 |
| ----------- | ------------------------------ |
| $N_w,\;N_v$ | 过程噪声样本数和观测噪声样本数 |
| $\bar w$ | 过程噪声样本均值 |
| $\bar v$ | 观测噪声样本均值 |
| $s_w^2$ | 过程噪声的**样本方差**估计 |
| $s_v^2$ | 观测噪声的**样本方差**估计 |
> **定义**：
> $$
> \bar w = \frac1{N_w}\sum_{i=1}^{N_w}w_i,\quad
> s_w^2 = \frac1{N_w-1}\sum_{i=1}^{N_w}(w_i-\bar w)^2,
> $$
>
> $$
> \bar v = \frac1{N_v}\sum_{j=1}^{N_v}v_j,\quad
> s_v^2 = \frac1{N_v-1}\sum_{j=1}^{N_v}(v_j-\bar v)^2.
> $$
---
### 3. 方差比的 $F$ 分布区间估计
1. **构造 $F$ 统计量**
$$
F = \frac{(s_w^2/Q)}{(s_v^2/R)}
= \frac{s_w^2}{s_v^2}\,\frac{R}{Q}
\sim F(N_w-1,\,N_v-1).
$$
2. **置信区间**（置信度 $1-\alpha$）
查得
$$
F_{L}=F_{\alpha/2}(N_w-1,N_v-1),\quad
F_{U}=F_{1-\alpha/2}(N_w-1,N_v-1),
$$
则
$$
\begin{align*}
P\Big\{F_{\rm L}\le F\le F_{\rm U}\Big\}=1-\alpha \quad\Longrightarrow \quad P\Big\{F_{\rm L}\,\le\frac{s_w^2}{s_v^2}\,\frac{R}{Q}\le F_{\rm U}\,\Big\}=1-\alpha.
\end{align*}
$$
3. **解出 $\frac{R}{Q}$ 的区间**
$$
P\Bigl\{\,F_{L}\,\frac{s_v^2}{s_w^2}\le \frac{R}{Q}\le F_{U}\,\frac{s_v^2}{s_w^2}\Bigr\}=1-\alpha.
$$
令
$$
\theta_{\min}=\sqrt{\,F_{L}\,\frac{s_v^2}{s_w^2}\,},\quad
\theta_{\max}=\sqrt{\,F_{U}\,\frac{s_v^2}{s_w^2}\,}.
$$
---
### 4. 卡尔曼增益与误差上界
在标量情况下（即状态和观测均为1维），卡尔曼增益公式可简化为：
$$
K = \frac{P_k H^T}{HP_k H^T + R} = \frac{HP_k}{H^2 P_k + R}
$$
针对我们研究对象，特征值滤波公式的系数都属于实数域。$P_{k-1}$是由上次迭代产生，因此可以$FP_{k-1}F^T$看作定值，则$P_k$的方差等于$Q$的方差，即： 针对我们研究对象，特征值滤波公式的系数都属于实数域。$P_{k-1}$是由上次迭代产生，因此可以$FP_{k-1}F^T$看作定值，则$P_k$的方差等于$Q$的方差，即：
@ -285,98 +366,42 @@ $$
\text{var}(P_k) = \text{var}(Q) \text{var}(P_k) = \text{var}(Q)
$$ $$
对卡尔曼增益$K$进行变换可得： 令 $c = H$, $m = 1/H$（满足 $cm = 1$），则：
$$ $$
K = \frac{1}{H + (H^T)^{-1} \cdot \left(\frac{R}{P_k}\right)} K = \frac{cP_k}{c^2 P_k + R} = \frac{1}{c + m(R/P_k)} \quad R/P_k\in[\theta_{\min}^2,\theta_{\max}^2].
$$
且方差满足：
$$
D\left(\frac{R}{P_k}\right) = \frac{\sigma_r}{\sigma_q}
$$
其中：
- $H$ 为观测矩阵
- $(H^T)^{-1}$ 表示观测矩阵转置的逆
- $\sigma_r$, $\sigma_q$ 分别为观测噪声和过程噪声的标准差
设$\{Q_1, Q_2, \cdots, Q_m\}$是属于$\{Q\}$的一组样本，$\{R_1, R_2, \cdots, R_n\}$是属于$\{R\}$的一组样本，由于过程噪声$Q$与观测噪声$R$都满足高斯分布则可知如下卡方分布：
$$
\sum_{i=1}^{n_q} \left( \frac{Q_i - \overline{Q}}{\sigma_q} \right)^2 \sim \chi^2(n_q - 1) \quad \text{(2-21)}
$$
$$
\sum_{i=1}^{n_r} \left( \frac{R_i - \overline{R}}{\sigma_r} \right)^2 \sim \chi^2(n_r - 1) \quad \text{(2-22)}
$$
对两式作变形可得$F$分布：
$$
\frac{\chi^{2}(n_{q})/(n_{q}-1)}{\chi^{2}(n_{r})/(n_{r}-1)} \sim F(n_{q}-1,n_{r}-1) \quad \text{(2-23)}
$$
观测噪声$Q$和过程噪声$R$比值$\sigma_{r}/\sigma_{q}$的区间估计满足：
$$
\frac{S_{q}^{*2}\sigma_{r}^{2}}{S_{r}^{*2}\sigma_{q}^{2}} \sim F(n_{q}-1,n_{r}-1)
$$
其中：
$$
S_{q}^{*2} = \frac{1}{n_{q}-1}\sum_{i=1}^{n_{q}}(Q_{i}-\overline{Q})^{2} \quad \text{(2-24)}
$$
$$
S_{r}^{*2} = \frac{1}{n_{r}-1}\sum_{i=1}^{n_{r}}(R_{i}-\overline{R})^{2} \quad \text{(2-25)}
$$
对于置信度为$1-\alpha$的情况：
$$
P\left\{F_{1-\alpha/2}(n_q-1,n_r-1) \leq \frac{S_{q}^{*2}\sigma_{r}^{2}}{S_{r}^{*2}\sigma_{q}^{2}} \leq F_{\alpha/2}(n_q-1,n_r-1)\right\}=1-\alpha \quad \text{(2-26)}
$$
于是可以得到：
$$
P\left\{F_{1-\alpha/2}(n_q-1,n_r-1)\frac{S_{r}^{*2}}{S_{q}^{*2}} \leq \frac{\sigma_{r}^{2}}{\sigma_{q}^{2}} \leq F_{\alpha/2}(n_q-1,n_r-1)\frac{S_{r}^{*2}}{S_{q}^{*2}}\right\}=1-\alpha \quad \text{(2-27)}
$$
我们采用绝对误差来进行精度分析，设$\xi$为绝对误差上限，即：
$$
\text{MSE}(\hat{x} - x) \leq \xi
$$
则有：
$$
\xi = \left( \frac{1}{c + m\theta_{min}} - \frac{1}{c + m\theta_{max}} \right) E\left( x_k' - x_k \right)
$$
$$
= \frac{m\left( \theta_{max} - \theta_{min} \right)}{(c + m\theta_{min}) \left( c + m\theta_{max} \right)} E\left( x_k' - x_k \right) \quad(2-28)
$$ $$
当$cm=1$时，可得： 则极值为
$$ $$
= \frac{(\theta_{max} - \theta_{min}) E \left( x_k' - x_k \right)}{(c^2 + \theta_{min}) (c^2 + \theta_{max})} K_{\max}=\frac{1}{c + m\,\theta_{\min}^2},\quad
K_{\min}=\frac{1}{c + m\,\theta_{\max}^2}.
\quad(2-29)
$$ $$
其中 $\theta_{min} = \left( F_{1-\alpha/2}(n_q - 1, n_r - 1) \frac{S_r^*}{S_q^*} \right)^{1/2}$，$\theta_{max} = \left( F_{\alpha/2}(n_q - 1, n_r - 1) \frac{S_r^*}{S_q^*} \right)^{1/2}$ 通过历史数据计算预测误差的均值：
$$
E(x_k' - x_k) \approx \frac{1}{M} \sum_{m=1}^{M} (x_k^{l(m)} - x_k^{(m)})\\
$$
定义误差上界
$$
\xi
=\bigl(K_{\max}-K_{\min}\bigr)\;E\bigl(x_k'-x_k\bigr)
=\Bigl(\tfrac1{c+m\,\theta_{\min}^2}-\tfrac1{c+m\,\theta_{\max}^2}\Bigr)
\,E(x_k'-x_k).
$$
若令 $c\,m=1$，可写成
$$
\xi
=\frac{(\theta_{\max}-\theta_{\min})\,E(x_k'-x_k)}
{(c^2+\theta_{\min})(c^2+\theta_{\max})}.
$$
---
根据上述推导，在获得预测模型的过程噪声与观测噪声后，可以根据区间估计的方法进行误差上界预估。 量化噪声方差估计的不确定性，进而评估卡尔曼滤波器增益的可能波动，并据此给出滤波误差的上界.

2
自学/Docker指南.md
View File

@ -120,7 +120,7 @@ docker image prune
​ -p <宿主机端口>:<容器端口> : 将容器内部的端口映射到宿主机，**使外部可以访问容器提供的服务，如果不写的话，只有容器内部网络能访问它**比如mysql，如果写''-p 3307:3306',那么可以用navicat连接localhost:3307访问这个数据库。 ​ -p <宿主机端口>:<容器端口> : 将容器内部的端口映射到宿主机，**使外部可以访问容器提供的服务，如果不写的话，只有容器内部网络能访问它**比如mysql，如果写''-p 3307:3306',那么可以用navicat连接localhost:3307访问这个数据库。
​ --restart <策略> :设置容器的重启策略，如 `no`（默认不重启）、`on-failure`（失败时重启）、`always`（总是重启）或 `unless-stopped`(最重要！docker服务重启时，它也跟着重启)。 ​ --restart <策略> :设置容器的重启策略，如 `no`（默认不重启）、`on-failure`（失败时重启）、`always`（总是重启）或 `unless-stopped`(最重要！docker服务重启时，它也跟着重启，但它不会读取最新的compose文件，只会恢复中断前容器内元数据)。
​ -v <宿主机目录>:<容器目录>` 或 `--volume ： 如 -v /host/data:/app/data ​ -v <宿主机目录>:<容器目录>` 或 `--volume ： 如 -v /host/data:/app/data

22
自学/JavaWeb——后端.md
View File

@ -1,5 +1,11 @@
# JavaWeb——后端 # JavaWeb——后端
## 好用的操作
右键文件/文件夹选择Copy Path/Reference，可以获得完整的包路径
## Java版本解决方案 ## Java版本解决方案
**单个Java文件运行：** **单个Java文件运行：**
@ -182,6 +188,8 @@ public class DeptController {
版本为2.7.3 版本为2.7.3
### 快速启动 ### 快速启动
1. 新建**spring initializr** project 1. 新建**spring initializr** project
@ -690,14 +698,14 @@ Component衍生注解
### 依赖注入 ### 依赖注入
1.Autowird注入 **1.Autowird注入**
```java ```java
@Autowired @Autowired
private PaymentClient paymentClient; // 字段直接加 @Autowired private PaymentClient paymentClient; // 字段直接加 @Autowired
``` ```
2.构造器注入（推荐） **2.构造器注入（推荐）**
1）手写构造器 1）手写构造器
@ -728,6 +736,8 @@ public class OrderService {
### 配置文件 ### 配置文件
#### 配置优先级 #### 配置优先级
@ -764,7 +774,7 @@ java -Dserver.port=9000 -jar XXXXX.jar --server.port=10010
#### **yml配置文件**(推荐！！!) #### yml配置文件(推荐！！!)
位置：`src/main/resources/application.yml` 位置：`src/main/resources/application.yml`
@ -805,7 +815,7 @@ private List<String> hobby;
#### **@ConfigurationProperties** #### @ConfigurationProperties
是用来**将外部配置（如 `application.properties` / `application.yml`）映射到一个 POJO** 上的。 是用来**将外部配置（如 `application.properties` / `application.yml`）映射到一个 POJO** 上的。
@ -927,7 +937,7 @@ public class CalculationService {
@Configuration // 配置类 @Configuration // 配置类
public class CommonConfig { public class CommonConfig {
// 定义第三方 Bean，并交给 IoC 容器管理 // 定义第三方 Bean，并交给 IoC 容器管理
@Bean // 返回值默认作为 Bean，Bean 名称默认为方法名 @Bean
public SAXReader reader(DeptService deptService) { public SAXReader reader(DeptService deptService) {
System.out.println(deptService); System.out.println(deptService);
return new SAXReader(); return new SAXReader();
@ -937,7 +947,7 @@ public class CommonConfig {
在应用启动时，Spring 会调用配置类中标注 `@Bean` 的方法，将方法**返回值注册**为容器中的 Bean 对象。 在应用启动时，Spring 会调用配置类中标注 `@Bean` 的方法，将方法**返回值注册**为容器中的 Bean 对象。
默认情况下，该 Bean 的名称就是**该方法的名字**。本例 Bean 名称默认就是 `"reader"`。 默认情况下，该 Bean 的名称就是**该方法的名字**。本例 Bean 名称默认就是 `"reader"`。Bean的类型就是返回值的类型，这里是`SAXReader`。

5
自学/Java笔记本.md
View File

@ -222,6 +222,7 @@ public void execute(OperationType type, Object entity) {
```java ```java
// 定义枚举类型 // 定义枚举类型
public enum DayOfWeek { public enum DayOfWeek {
//创建7个 DayOfWeek 类型的对象，分别传入构造参数chineseName和dayNumber
MONDAY("星期一", 1), MONDAY("星期一", 1),
TUESDAY("星期二", 2), TUESDAY("星期二", 2),
WEDNESDAY("星期三", 3), WEDNESDAY("星期三", 3),
@ -260,6 +261,10 @@ public class Main {
} }
``` ```
**枚举类你只需要使用，而不用创建对象**，类内部已经定义好了MONDAY、TUESDAY...对象。
#### Java传参方式 #### Java传参方式

12
自学/Mybatis&-Plus.md
View File

@ -538,7 +538,13 @@ public class User {
} }
``` ```
这个例子会，映射到数据库中的user_detail表，主键为id_dd，并且插入时采用数据库自增，相当于开启`useGeneratedKeys=true`，执行完 `insert(user)` 后，`user.getId()` 就会是数据库分配的主键值，否则默认获得null，但不影响数据表中的内容。 这个例子会，映射到数据库中的user_detail表，主键为id_dd，并且插入时采用数据库自增；能自动回写主键，相当于开启`useGeneratedKeys=true`，执行完 `insert(user)` 后，`user.getId()` 就会是数据库分配的主键值，否则默认获得null，但不影响数据表中的内容。
`type=dType.ASSIGN_ID` 表示用雪花算法生成密码，更加复杂，而不是简单的AUTO自增。它也能自动回写主键。
@ -1051,6 +1057,10 @@ public List<UserVO> queryUsers(UserQuery query){
} }
``` ```
`.eq(status != null, User::getStatus, status)`，使用`User::getStatus`方法引用并不直接把'Status'插入到 SQL，而是在运行时会被 MyBatis-Plus 解析成实体属性 `Status`”对应的数据库列是 `status`。推荐!!!
可以发现lambdaQuery方法中除了可以构建条件，还需要在链式编程的最后添加一个`list()`，这是在告诉MP我们的调用结果需要是一个list集合。这里不仅可以用`list()`，可选的方法有： 可以发现lambdaQuery方法中除了可以构建条件，还需要在链式编程的最后添加一个`list()`，这是在告诉MP我们的调用结果需要是一个list集合。这里不仅可以用`list()`，可选的方法有：
- `.one()`：最多1个结果 - `.one()`：最多1个结果

52
自学/力扣Hot 100题.md
View File

@ -291,18 +291,26 @@ public static List<String> splitBySpace(String s) {
6.**`reverse()`** 6.**`reverse()`**
将字符串反转。String未提供 将字符串反转。String未提供
**重要内容！！！！**
7.**`toString()`** 7.**`toString()`**
返回当前字符串缓冲区的内容，转换为 `String` 对象。 返回当前字符串缓冲区的内容，转换为 `String` 对象。
`sb.toString()`会创建并返回一个新的、独立的 `String` 对象，之后`setLength(0)`不会影响这个 `String` 对象 `sb.toString()`会创建并返回一个**新的、独立**的 `String` 对象，之后`setLength(0)`不会影响这个 `String` 对象
8.**`charAt(int index)`** 8.**`setLength(int newLength)`**
设置字符串的长度。 //sb.setLength(0); 用作清空字符串
9.**`charAt(int index)`**
返回指定位置的字符。 返回指定位置的字符。
9.**`length()`** 10.**`length()`**
返回当前字符串的长度。 返回当前字符串的长度。
10.**`setLength(int newLength)`**
设置字符串的长度。 //sb.setLength(0); 用作清空字符串
@ -726,6 +734,12 @@ list2.addAll(list1); //法一
List<Integer> list2 = new ArrayList<>(list1); //法二 List<Integer> list2 = new ArrayList<>(list1); //法二
``` ```
复制链表到数组：
推荐老实遍历+添加。java自带方法有点复杂。
清空(list set map queue map都有clear方法): 清空(list set map queue map都有clear方法):
```java ```java
@ -2253,6 +2267,34 @@ public int multipleKnapsack(int V, int[] weight, int[] value, int[] count) {
### 并查集
```java
for (int i = 0; i < 26; i++) {
parent[i] = i; //初始化
}
public void union(int[] parent, int index1, int index2) {
// 先分别找到 index1 和 index2 的根节点，再把 root(index1) 的父指针指向 root(index2)
parent[find(parent, index1)] = find(parent, index2);
}
//查找 index 元素所在集合的根节点（同时做路径压缩）
public int find(int[] parent, int index) {
// 当 parent[index] == index 时，说明已经是根节点
while (parent[index] != index) {
// 路径压缩：将当前节点直接挂到它父节点的父节点上
// 这样可以让树变得更扁平，后续查找更快
parent[index] = parent[parent[index]];
// 跳到上一级，继续判断是否到根
index = parent[index];
}
// 循环结束时，index 即为根节点下标
return index;
}
```
## ACM风格输入输出 ## ACM风格输入输出
```text ```text

48
自学/微服务.md
View File

@ -164,7 +164,7 @@ mysql是服务名，不能写localhost（或 `127.0.0.1`），它永远只会指
### Docker Compose问题 ### Docker Compose问题
如果你把某个服务从 `docker-compose.yml` 里删掉，然后再执行： 1）如果你把某个服务从 `docker-compose.yml` 里删掉，然后再执行：
```shell ```shell
docker compose down docker compose down
@ -188,6 +188,52 @@ docker rm <container_id_or_name>
2）端口占用问题
Error response from daemon: Ports are not available: exposing port TCP 0.0.0.0:5672 -> 0.0.0.0:0: listen tcp 0.0.0.0:5672: bind: An attempt was made to access a socket in a way forbidden by its access permissions.
先查看是否端口被占用：
```shell
netstat -aon | findstr 5672
```
如果没有被占用，那么就是windows的bug，在CMD使用管理员权限重启NAT网络服务即可
```shell
net stop winnat
net start winnat
```
3）ip地址问题
```yml
seata-server:
image: seataio/seata-server:1.5.2
container_name: seata-server
restart: unless-stopped
depends_on:
- mysql
- nacos
environment:
# 指定 Seata 注册中心和配置中心地址
- SEATA_IP=192.168.10.218 # IDEA 可以访问到的宿主机 IP
- SEATA_SERVICE_PORT=17099
- SEATA_CONFIG_TYPE=file
# 可视情况再加：SEATA_NACOS_SERVER_ADDR=nacos:8848
networks:
- hmall-net
ports:
- "17099:7099" # TC 服务端口
- "8099:8099" # 服务管理端口（Console）
volumes:
- ./seata:/seata-server/resources
```
SEATA_IP配置的是宿主机IP，你的电脑换了IP，如从教室到寝室，那这里的IP也要跟着变：ipconfig查看宿主机ip
## 认识微服务 ## 认识微服务

25
自学/智能协同云图库.md Normal file
View File

@ -0,0 +1,25 @@
# 智能协同云图库
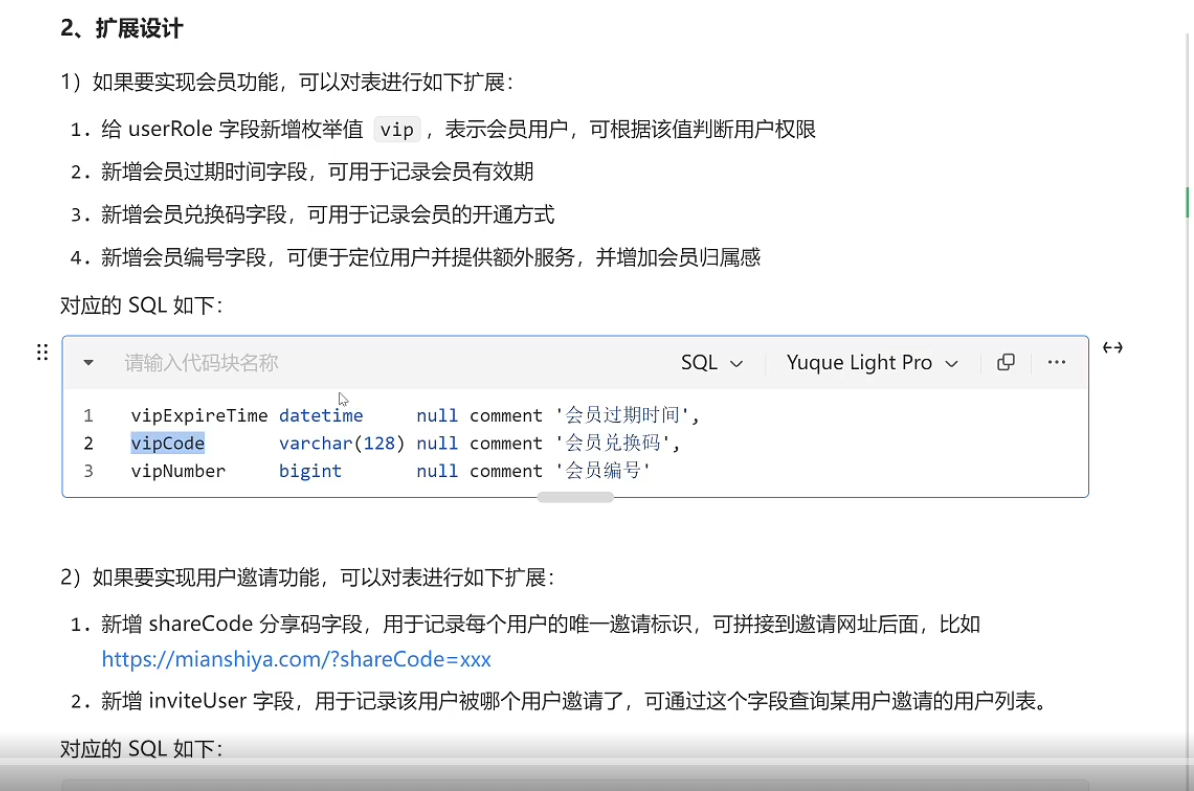
用户模块扩展功能：
![image-20250605171423657](https://pic.bitday.top/i/2025/06/05/scmgpj-0.png)
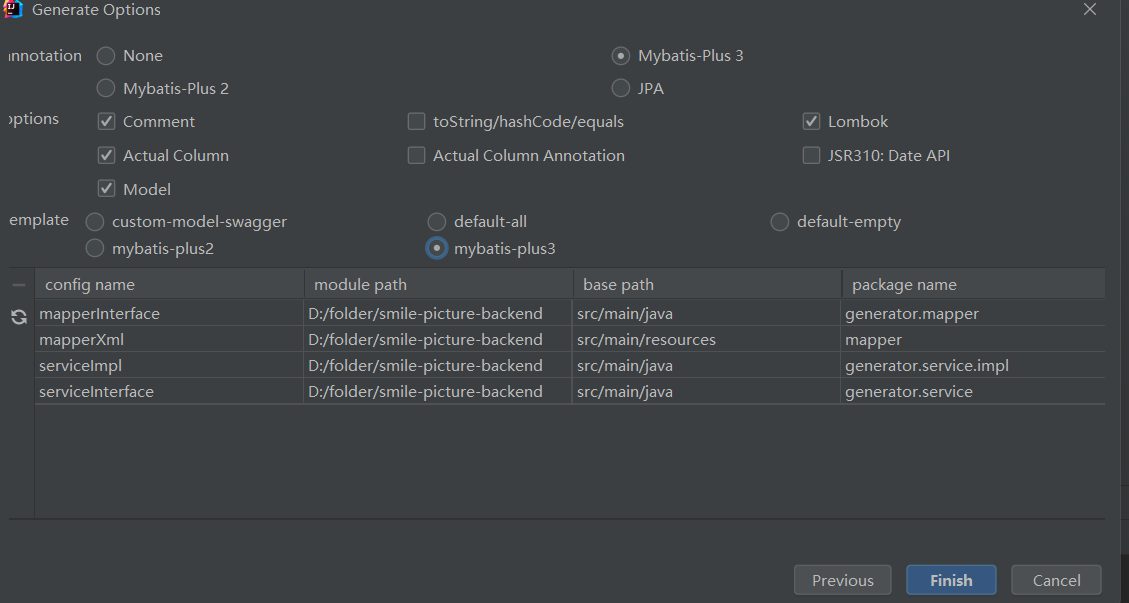
下载MybatisX插件，可以从数据表直接生成Bean、Mapper、Service，选项设置如下：
注意，勾选Actual Column生成的Bean和表中字段一模一样，取消勾选会进行驼峰转换，即user_name->userName
![image-20250605174225328](https://pic.bitday.top/i/2025/06/05/st9hiz-0.png)
![image-20250605174413935](https://pic.bitday.top/i/2025/06/05/sudrtc-0.png)
下载GenerateSerailVersionUID插件，可以右键->generate->生成序列ID：
```java
private static final long serialVersionUID = -1321880859645675653L;
```
![image-20250605181008973](https://pic.bitday.top/i/2025/06/05/txnduw-0.png)

368
自学/消息队列MQ.md
View File

@ -31,23 +31,26 @@
### 部署 ### 部署
```yml ```yml
mq: mq: #消息队列
image: rabbitmq:3.8-management image: rabbitmq:3.8-management
container_name: mq container_name: mq
restart: unless-stopped restart: unless-stopped
hostname: mq hostname: mq
environment: environment:
- TZ=Asia/Shanghai TZ: "Asia/Shanghai"
RABBITMQ_DEFAULT_USER: admin RABBITMQ_DEFAULT_USER: admin
RABBITMQ_DEFAULT_PASS: "admin" RABBITMQ_DEFAULT_PASS: "admin"
RABBITMQ_PLUGINS_DIR: "/plugins:/custom-plugins"
ports: ports:
- "15672:15672" - "15672:15672"
- "5672:5672" - "5672:5672"
volumes: volumes:
- ./mq-plugins:/custom-plugins - mq-plugins:/plugins
# 持久化数据卷，保存用户/队列/交换机等元数据
- ./mq-data:/var/lib/rabbitmq
networks: networks:
- hmall-net - hmall-net
volumes:
mq-plugins:
``` ```
http://localhost:15672/ 访问控制台 http://localhost:15672/ 访问控制台
@ -104,7 +107,7 @@ spring:
**消息发送：** **消息发送：**
然后在`publisher`服务中编写测试类`SpringAmqpTest`，并利用`RabbitTemplate`实现消息发送： 然后在`publisher`服务中编写测试类`SpringAmqpTest`，并利用**`RabbitTemplate`**实现消息发送：
```java ```java
@SpringBootTest @SpringBootTest
@ -203,19 +206,17 @@ BindingKey一般都是有一个或**多个单词**组成，多个单词之间以
### 基于注解声明交换机队列 ### 基于注解声明交换机、队列
以往我们都在 RabbitMQ 管理控制台手动创建队列和交换机，开发人员还得把所有配置整理一遍交给运维，既繁琐又容易出错。更好的做法是在应用启动时自动检测所需的队列和交换机，若不存在则直接创建。 以往我们都在 RabbitMQ 管理控制台手动创建队列和交换机，开发人员还得把所有配置整理一遍交给运维，既繁琐又容易出错。更好的做法是在应用启动时自动检测所需的队列和交换机，若不存在则直接创建。
**基于注解方式来声明** **基于注解方式来声明**
`durable="true"`：队列在 RabbitMQ 重启后依然存在。
`type` 默认交换机类型为ExchangeTypes.DIRECT `type` 默认交换机类型为ExchangeTypes.DIRECT
```java ```java
@RabbitListener(bindings = @QueueBinding( @RabbitListener(bindings = @QueueBinding(
value = @Queue(name = "direct.queue1",durable = "true"), value = @Queue(name = "direct.queue1"),
exchange = @Exchange(name = "hmall.direct", type = ExchangeTypes.DIRECT), exchange = @Exchange(name = "hmall.direct", type = ExchangeTypes.DIRECT),
key = {"red", "blue"} key = {"red", "blue"}
)) ))
@ -253,6 +254,8 @@ public void listenDirectQueue2(String msg){
使用JSON方式来做序列化和反序列化，替换掉默认方式。 使用JSON方式来做序列化和反序列化，替换掉默认方式。
更小或可压缩的消息体、易读、易调试
1）引入依赖 1）引入依赖
```XML ```XML
@ -276,3 +279,350 @@ public MessageConverter messageConverter(){
} }
``` ```
## MQ高级
我们要解决消息丢失问题，保证MQ的可靠性，就必须从3个方面入手：
- 确保生产者一定把消息发送到MQ
- 确保MQ不会将消息弄丢
- 确保消费者一定要处理消息
### 发送者的可靠性
#### **发送者重试**
修改发送者模块的`application.yaml`文件，添加下面的内容：
```YAML
spring:
rabbitmq:
connection-timeout: 1s # 设置MQ的连接超时时间
template:
retry:
enabled: true # 开启超时重试机制
initial-interval: 1000ms # 失败后的初始等待时间
multiplier: 1 # 失败后下次的等待时长倍数，下次等待时长 = initial-interval * multiplier
max-attempts: 3 # 最大重试次数
```
- *阻塞重试，一般不建议开启。*
#### **发送者确认**
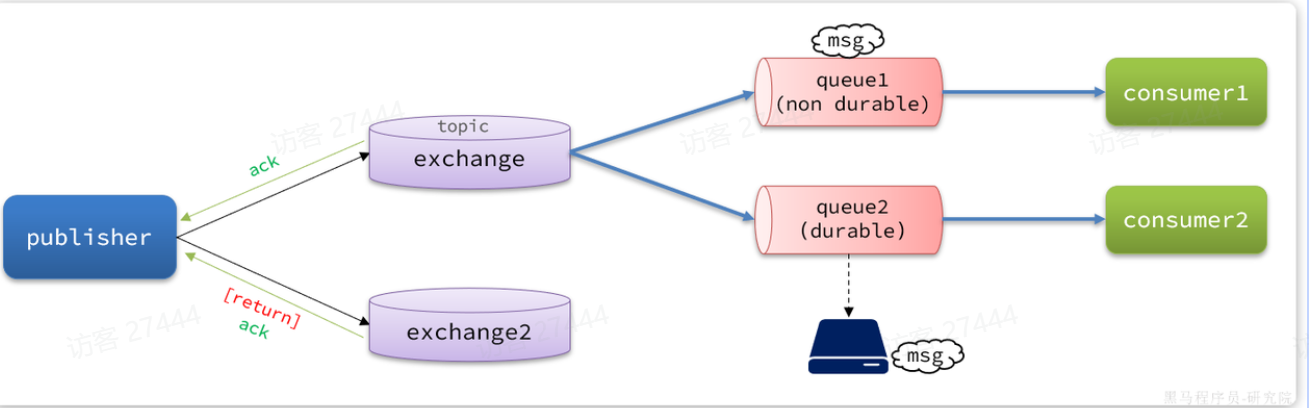
![image-20250529170017117](https://pic.bitday.top/i/2025/05/29/s49oln-0.png)
- 当消息投递到MQ，但是**路由失败**（没有队列绑定交换机、或者你routingKey设置错误等）时，通过**Publisher Return**返回异常信息，同时返回ack的确认信息，代表投递成功
- 临时消息投递到了MQ，并且入队成功，返回ACK，告知投递成功
- 持久消息投递到了MQ，并且入队完成持久化，返回ACK ，告知投递成功
- 其它情况都会返回NACK，告知投递失败
1.在发送者模块的`application.yaml`中添加配置：
```YAML
spring:
rabbitmq:
publisher-confirm-type: correlated # 开启publisher confirm机制，并设置confirm类型
publisher-returns: true # 开启publisher return机制
```
- `none`：关闭confirm机制
- `simple`：同步阻塞等待MQ的回执
- `correlated`：MQ异步回调返回回执
2.每个`RabbitTemplate`只能配置一个`ReturnCallback`，因此我们可以在**配置类**中统一设置。我们在publisher模块定义一个配置类：
```java
@Slf4j
@RequiredArgsConstructor
@Configuration
public class MqConfig {
private final RabbitTemplate rabbitTemplate;
@PostConstruct
public void init(){
rabbitTemplate.setReturnsCallback(new RabbitTemplate.ReturnsCallback() {
@Override
public void returnedMessage(ReturnedMessage returned) {
log.error("触发return callback,");
log.debug("exchange: {}", returned.getExchange());
log.debug("routingKey: {}", returned.getRoutingKey());
log.debug("message: {}", returned.getMessage());
log.debug("replyCode: {}", returned.getReplyCode());
log.debug("replyText: {}", returned.getReplyText());
}
});
}
}
```
3.定义ConfirmCallback
由于每个消息发送时的处理逻辑不一定相同，因此ConfirmCallback需要在每次发消息时定义。具体来说，是在调用RabbitTemplate中的convertAndSend方法时，多传递一个参数：
![image-20250529180404355](https://pic.bitday.top/i/2025/05/29/tu2fve-0.png)
这里的CorrelationData中包含两个核心的东西：
- `id`：消息的唯一标示，MQ对不同的消息的回执以此做判断，避免混淆
- `SettableListenableFuture`：回执结果的Future对象
```java
@Test
void testPublisherConfirm() {
// 1.创建CorrelationData
CorrelationData cd = new CorrelationData();
// 2.给Future添加ConfirmCallback
cd.getFuture().addCallback(new ListenableFutureCallback<CorrelationData.Confirm>() {
@Override
public void onFailure(Throwable ex) {
// 2.1.Future发生异常时的处理逻辑，基本不会触发
log.error("send message fail", ex);
}
@Override
public void onSuccess(CorrelationData.Confirm result) {
// 2.2.Future接收到回执的处理逻辑，参数中的result就是回执内容
if(result.isAck()){ // result.isAck()，boolean类型，true代表ack回执，false 代表 nack回执
log.debug("发送消息成功，收到 ack!");
}else{ // result.getReason()，String类型，返回nack时的异常描述
log.error("发送消息失败，收到 nack, reason : {}", result.getReason());
}
}
});
// 3.发送消息
rabbitTemplate.convertAndSend("hmall.direct", "q", "hello", cd);
}
```
**端到端投递保障**
- **ConfirmCallback** 只告诉你：消息“到”了 RabbitMQ 服务器吗？（ACK：到；NACK：没到）
- **ReturnsCallback** 只告诉你：到达服务器的消息，能“进”队列吗？（能进就不回；进不了就退）
两者都成功，才能确认：“这条消息真的安全地进了队列，等着消费者去拿。”
- *开启生产者确认比较消耗MQ性能，一般不建议开启。*
### MQ的可靠性
#### 数据持久化
为了保证数据的可靠性，必须配置数据持久化（从内存保存到磁盘上），包括：
- 交换机持久化（选Durable）
- 队列持久化（选Durable）
- 消息持久化（选Persistent）
控制台方式：
![image-20250530154302987](https://pic.bitday.top/i/2025/05/30/pipl8z-0.png)
![image-20250530154321546](https://pic.bitday.top/i/2025/05/30/pis74e-0.png)
这样重启后还能恢复。
代码方式，默认都是持久化的，不用变动。
### 消费者可靠性
#### 消费者确认机制
当消费者**处理消息结束**后，向RabbitMQ返回自己的处理状态，MQ做出相应反应...
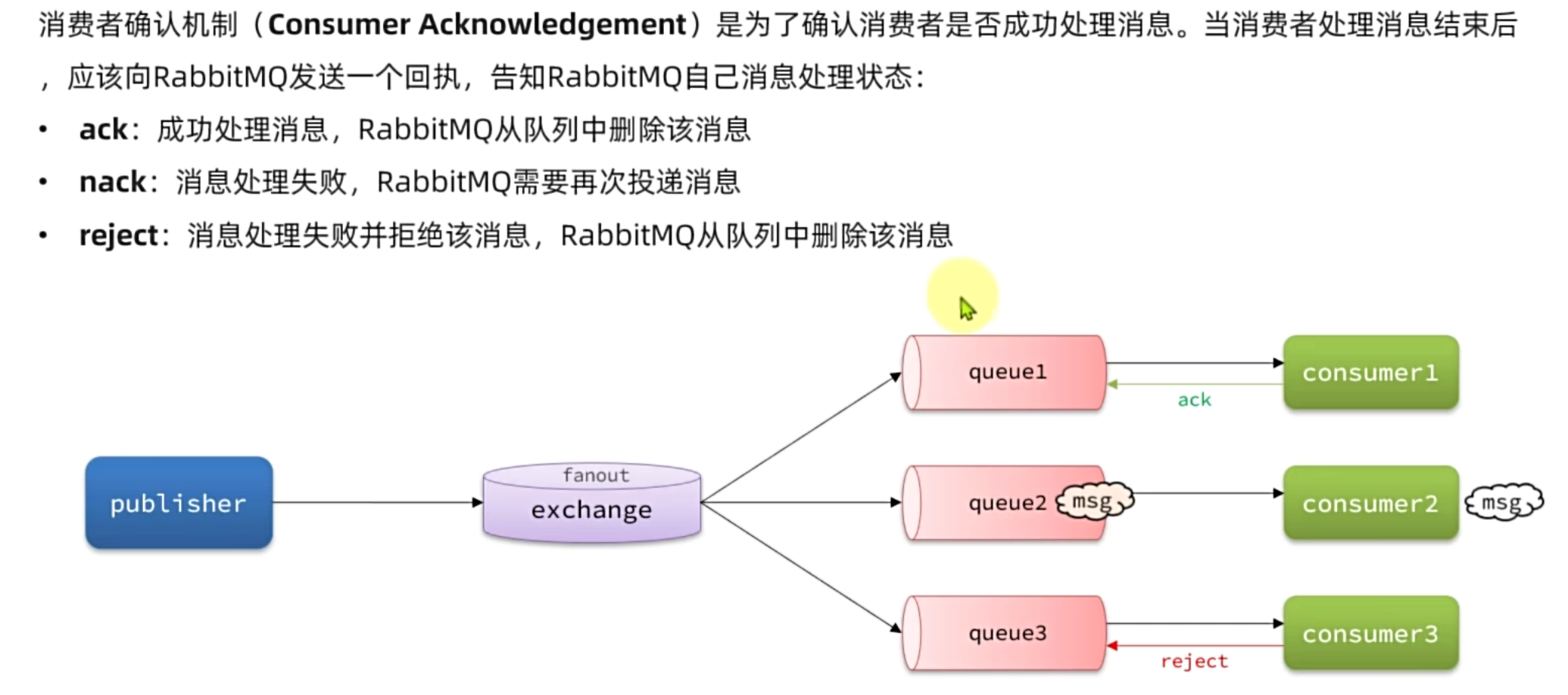
![image-20250530160814244](https://pic.bitday.top/i/2025/05/30/qlfwrn-0.png)
上述的NACK状态时，MQ会**不断向消费者重投**消息，直至被正确处理！！！
在消费者方，通过下面的配置可以修改消费者收到消息后的ACK处理方式：
none,收到消息就直接返回ack；
manual，手动实现ack；
**auto**，自动档，业务异常返回nack， 消息处理异常返回reject，其他ack （默认也是这个模式）
```yaml
spring:
rabbitmq:
listener:
simple:
acknowledge-mode: auto
```
#### 消费者重试
- 类似发送者的重试机制，在消费者出现异常时利用**本地重试**，而不是无限制的requeue到mq队列。
- 重试达到最大次数后，、会返回reject，消息会被丢弃
修改consumer服务的application.yml文件，添加内容：
```YAML
spring:
rabbitmq:
listener:
simple:
retry:
enabled: true # 开启消费者失败重试
initial-interval: 1000ms # 初识的失败等待时长为1秒
multiplier: 1 # 失败的等待时长倍数，下次等待时长 = multiplier * last-interval
max-attempts: 3 # 最大重试次数
stateless: true # true无状态；false有状态。如果业务中包含事务，这里改为false
```
**Stateless（无状态重试）**：所有的重试都在**同一个事务上下文**里进行，直到重试次数用尽后才会把异常抛回容器并最终回滚或提交事务。
**Stateful（有状态重试）**：每次重试都会被当成一次**独立**的消息交付，Spring 会为每次尝试开启新的事务，失败时立即回滚并重新投递，下次重试又是一个干净的事务环境。这对事务性操作(@Transactional)来说，能保证“第 N 次重试失败就回滚第 N 次的事务”，避免把所有尝试都裹在一笔大事务里
#### 失败处理策略
前面默认的达到最大重试次数后，消息会被丢弃，对于消息可靠性要求较高的业务场景下，显然不太合适了。
因此Spring允许我们自定义重试次数耗尽后的消息处理策略，这个策略是由`MessageRecovery`接口来定义的，它有3个不同实现：
- `RejectAndDontRequeueRecoverer`：重试耗尽后，直接`reject`，丢弃消息。默认就是这种方式
- `ImmediateRequeueMessageRecoverer`：重试耗尽后，返回`nack`，消息重新入队
- `RepublishMessageRecoverer`：重试耗尽后，将失败消息投递到指定的交换机
比较优雅的一种处理方案是`RepublishMessageRecoverer`，失败后将消息投递到一个指定的，专门存放异常消息的交换机->队列，后续由人工集中处理。
#### 业务幂等性
在程序开发中，幂等则是指同一个业务，执行一次或多次对业务状态的影响是一致的。如：
- 根据id删除数据
- 查询数据
- 新增数据
但数据的更新往往不是幂等的，如果重复执行可能造成不一样的后果。比如：
- 取消订单，恢复库存的业务。如果多次恢复就会出现库存重复增加的情况
- 退款业务。重复退款对商家而言会有经济损失。
**所以，我们要尽可能避免业务被重复执行：MQ消息的重复投递、页面卡顿时频繁刷新导致表单重复提交、服务间调用的重试**
法一：唯一ID
1. 每一条消息都生成一个唯一的id，与消息一起投递给消费者。
2. 消费者接收到消息后处理自己的业务，业务处理成功后将消息ID保存到数据库
3. 如果下次又收到相同消息，去数据库查询判断是否存在，存在则为重复消息放弃处理。
法一存在业务侵入，因为mq的消息ID与业务无关，现在却多了一张专门记录 ID 的表或结构
法二：业务判断，基于业务本身的逻辑或状态来判断是否是重复的请求或消息，不同的业务场景判断的思路也不一样。
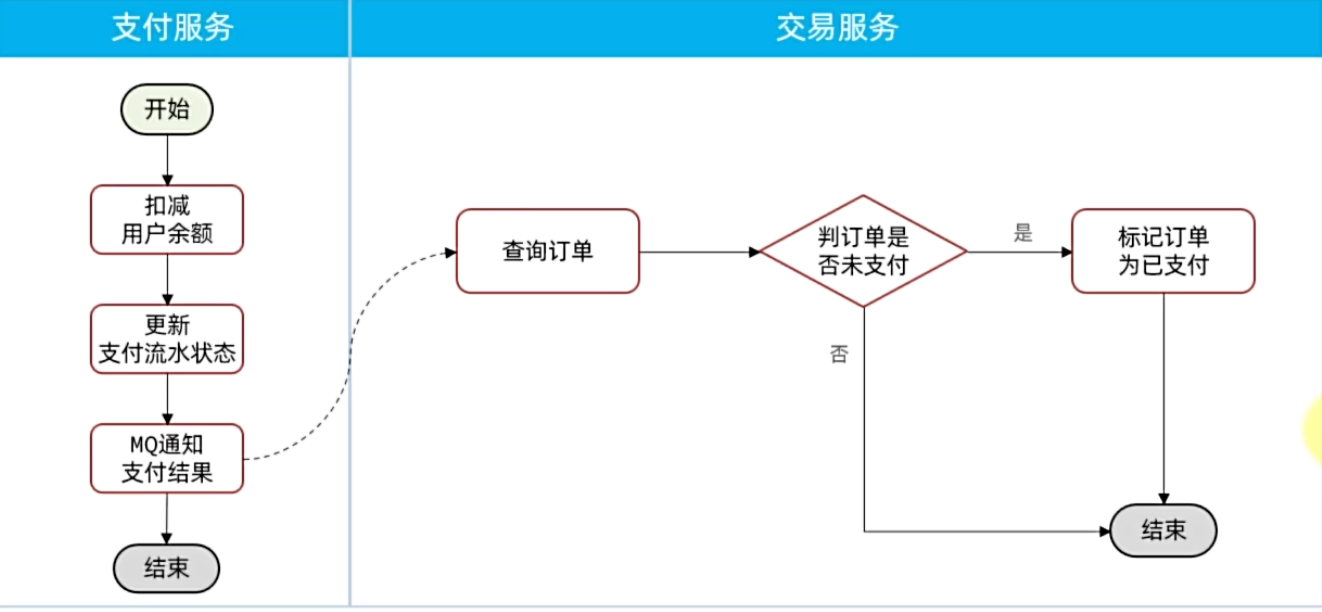
![image-20250603151010579](https://pic.bitday.top/i/2025/06/03/oz399u-0.png)
综上，支付服务与交易服务之间的订单状态一致性是如何保证的？
- 首先，支付服务会正在用户支付成功以后利用MQ消息通知交易服务，完成订单状态同步。
- 其次，为了保证MQ消息的可靠性，我们采用了生产者确认机制、消费者确认、消费者失败重试等策略，确保消息投递的可靠性
- 最后，我们还在交易服务设置了定时任务，定期查询订单支付状态。这样即便MQ通知失败，还可以利用定时任务作为兜底方案，确保订单支付状态的最终一致性。
### 延迟消息
对于超过一定时间未支付的订单，应该立刻取消订单并释放占用的库存。
例如，订单支付超时时间为30分钟，则我们应该在用户下单后的第30分钟检查订单支付状态，如果发现未支付，应该立刻取消订单，释放库存。
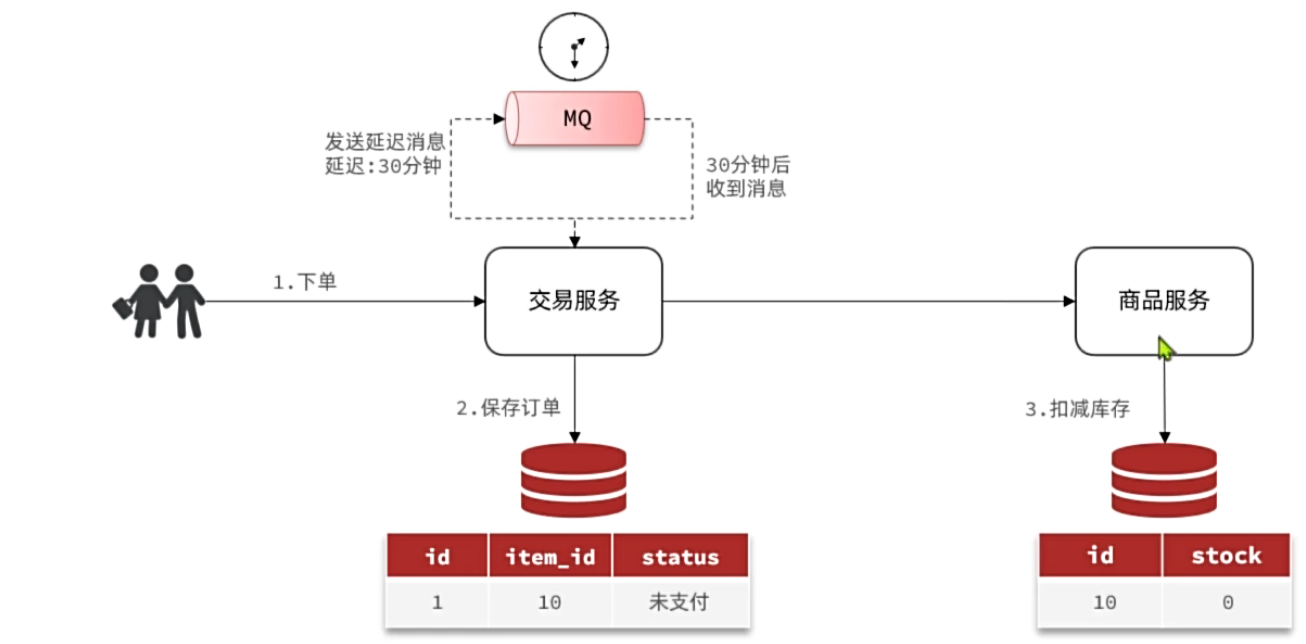
![image-20250603154136058](https://pic.bitday.top/i/2025/06/03/phnk4w-0.png)
#### 延迟消息插件
1.下载
[GitHub - rabbitmq/rabbitmq-delayed-message-exchange: Delayed Messaging for RabbitMQ](https://github.com/rabbitmq/rabbitmq-delayed-message-exchange)
2.上传插件，由于之前docker部署MQ挂载了数据卷
```shell
docker volume ls #查看所有数据卷
docker volume inspect hmall_all_mq-plugins #获取数据卷的目录
#"Mountpoint": "/var/lib/docker/volumes/hmall_all_mq-plugins/_data"
```
我们上传插件到该目录下。
3.安装插件
```shell
docker exec -it mq rabbitmq-plugins enable rabbitmq_delayed_message_exchange
```
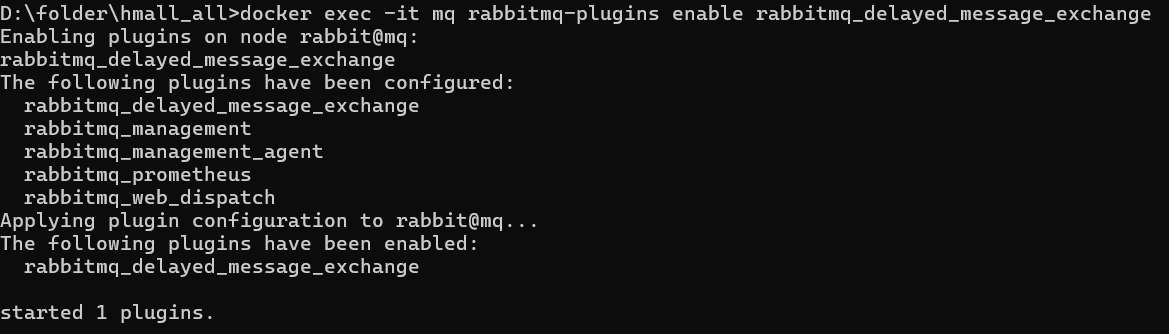
![image-20250603163744968](https://pic.bitday.top/i/2025/06/03/r2v3hh-0.png)
#### 声明延迟交换机
额外指定参数 `delayed = "true"`
```Java
@RabbitListener(bindings = @QueueBinding(
value = @Queue(name = "delay.queue", durable = "true"),
exchange = @Exchange(name = "delay.direct", delayed = "true"),
key = "delay"
))
public void listenDelayMessage(String msg){
log.info("接收到delay.queue的延迟消息：{}", msg);
}
```
#### 发送延迟消息
```Java
@Test
void testPublisherDelayMessage() {
// 1.创建消息
String message = "hello, delayed message";
// 2.发送消息，利用消息后置处理器添加消息头
rabbitTemplate.convertAndSend("delay.direct", "delay", message, new MessagePostProcessor() {
@Override
public Message postProcessMessage(Message message) throws AmqpException {
// 添加延迟消息属性
message.getMessageProperties().setDelay(5000);
return message;
}
});
}
```
#### 超时订单问题
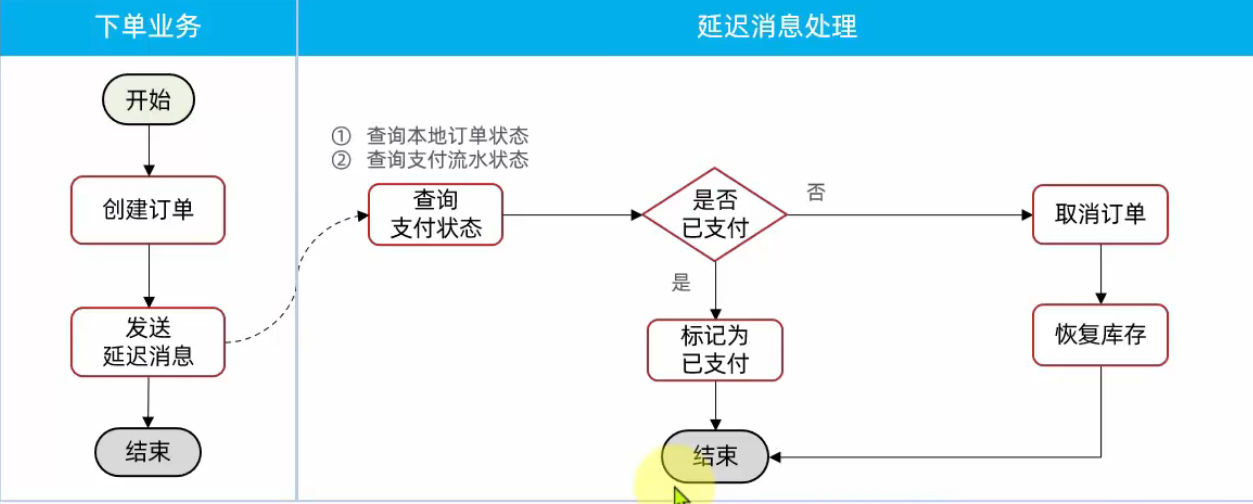
![image-20250603171922542](https://pic.bitday.top/i/2025/06/03/sfjqx5-0.png)
三种可能性：1.如果用户支付成功，但是消息通知失败（未传递给订单服务），那么会导致数据不一致情况，这时延迟消息到达后，它会先看本地订单状态，发现处于'待支付'状态，此时不确定是否是真的未支付，还是消息通知失败，需要再openfeign调用支付服务，查询支付流水状态，发现支付成功，那么就更新本地订单状态为'已支付'。
2.如果用户支付成功且消息通知成功，那么订单服务会更新订单状态为'已支付'，延迟消息到达时查询本地订单状态，确实'已支付'，直接return。
3.用户确实到时间了扔未支付，此时本地订单状态和远程的支付流水状态都是'待支付'，此时取消订单、恢复库存。

44
自学/苍穹外卖.md
View File

@ -95,7 +95,9 @@ postman: 接口测工具，模拟用户发起的各类HTTP请求，获取对应
1.构建和打包前端项目 1.构建和打包前端项目
```bash ```bash
npm run build npm install #安装依赖
npm run build #打包，但我TypeScript 检查报错
npm run pure-build #不检查类型打包
``` ```
2.将构建文件复制到指定目录 2.将构建文件复制到指定目录
@ -216,6 +218,25 @@ nginx.exe -s stop
#### **跨域问题产生方式：**
- 你在地址栏输 `http://localhost:8100/api/health`，这是浏览器直接导航到该 URL——浏览器会绕过 CORS 机制，直接向服务器发请求并渲染响应结果，这种场景不受 CORS 限制。
- 但如果你在一个在 `http://localhost:3000`（或任何不同端口）下运行的前端网页里，用 JavaScript 这样写：
```js
fetch('http://localhost:8100/api/health')
.then(res => res.json())
.then(data => console.log(data))
.catch(err => console.error(err));
```
会触发跨域
#### Nginx #### Nginx
**1.静态资源托管** **1.静态资源托管**
@ -253,6 +274,27 @@ server {
- 统一入口**解决跨域**问题（无需后端配置 CORS）。 - 统一入口**解决跨域**问题（无需后端配置 CORS）。
```java
@Configuration
public class CorsConfig implements WebMvcConfigurer {
@Override
public void addCorsMappings(CorsRegistry registry) {
// 覆盖所有请求
registry.addMapping("/**")
// 允许发送 Cookie
.allowCredentials(true)
// 放行哪些域名（必须用 patterns，否则 * 会和 allowCredentials 冲突）
.allowedOriginPatterns("*")
.allowedMethods("GET", "POST", "PUT", "DELETE", "OPTIONS")
.allowedHeaders("*")
.exposedHeaders("*");
}
}
```
**nginx 反向代理的配置方式：** **nginx 反向代理的配置方式：**
```nginx ```nginx