Commit on 2025/07/28 周一 21:28:40.93
This commit is contained in:
parent
3f0c608c84
commit
5d682e6b30
@ -2079,9 +2079,9 @@ public boolean canFillBackpack(int[] weights, int capacity) {
|
||||
dp[j] 表示从数组中选取若干个数,使得这些数的和正好为 j 的方法数。
|
||||
|
||||
状态转移:
|
||||
对于数组中的每个数字 numnumnum,从 dp 数组后向前(逆序)遍历,更新:
|
||||
对于数组中的每个数字 `num`,从 dp 数组后向前(逆序)遍历,更新:
|
||||
|
||||
dp[j]=dp[j]+dp[j−num]
|
||||
`dp[j]=dp[j]+dp[j−num]`
|
||||
|
||||
这里的意思是:
|
||||
|
||||
@ -2102,7 +2102,7 @@ dp[j]=dp[j]+dp[j−num]
|
||||
|
||||
#### 0/1背包(一)
|
||||
|
||||
描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品只能用一次**,求解将哪些物品装入背包里物品价值总和最大。
|
||||
描述:有n件物品和一个最多能背重量为 w 的背包。第 i 件物品的重量是 weight[i],得到的价值是 value[i] 。**每件物品只能用一次**,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/11/r292zm-0.png" alt="image-20250411163635562" style="zoom: 80%;" />
|
||||
|
||||
@ -2116,18 +2116,18 @@ dp[j]=dp[j]+dp[j−num]
|
||||
|
||||
**2. 确定递推公式**
|
||||
|
||||
考虑dp\[i][j],有两种情况:
|
||||
考虑 `dp[i][j]`,有两种情况:
|
||||
|
||||
- **不放物品i**:背包容量为j,里面不放物品i的最大价值是 dp\[i - 1][j]。
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为 j - weight[i],dp\[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp\[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
- **不放物品i**:背包容量为 `j` ,里面不放物品 `i` 的最大价值是 `dp[i - 1][j]`。
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为 `j - weight[i]`,`dp[i - 1][j - weight[i]]` 为背包容量为`j - weight[i]` 且不放物品i的最大价值,那么`dp[i - 1][j - weight[i]] + value[i]` (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
递归公式: `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
|
||||
|
||||
**3. dp数组如何初始化**
|
||||
|
||||
(1)首先从dp\[i][j]的定义出发,如果背包容量j为0的话,即dp\[i][0],无论是选取哪些物品,背包价值总和一定为0。
|
||||
(1)首先从 `dp[i][j]` 的定义出发,如果背包容量 `j` 为0的话,即 `dp[i][0]` ,无论是选取哪些物品,背包价值总和一定为0。
|
||||
|
||||
(2)由状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
(2)由状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 可以看出`i` 是由 `i-1` 推导出来,那么 `i` 为0的时候就一定要初始化。
|
||||
|
||||
此时就看存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
@ -2156,7 +2156,7 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
|
||||
**代码:**
|
||||
|
||||
```
|
||||
```java
|
||||
public int knapsack(int[] weight, int[] value, int capacity) {
|
||||
int n = weight.length; // 物品的总个数
|
||||
|
||||
@ -2202,11 +2202,11 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
|
||||
1.状态转移只依赖于之前的状态(例如上一行或上一个层次),而不是当前行中动态更新的状态。
|
||||
|
||||
- 例如在 0/1 背包问题中,二维 dp\[i][j] 只依赖于 dp\[i-1][j] 和 dp\[i-1][j - weight[i]]。
|
||||
- 例如在 0/1 背包问题中,二维 `dp[i][j]` 只依赖于 `dp[i-1][j]` 和 `dp[i-1][j - weight[i]]`。
|
||||
|
||||
2.存在确定的遍历顺序(例如逆序或正序)能够确保在更新一维 dp 时,所依赖的值不会被当前更新覆盖。
|
||||
|
||||
- **逆序遍历**:例如 0/1 背包问题,为了防止同一个物品被重复使用,需要对容量 j 从大到小遍历,确保 dp[j - weight] 的值还是上一轮(上一行)的。
|
||||
- **逆序遍历**:例如 0/1 背包问题,为了防止同一个物品被重复使用,需要对容量 j 从大到小遍历,确保 `dp[j - weight]` 的值还是上一轮(上一行)的。
|
||||
|
||||
- **正序遍历**:在一些问题中,如果状态更新不会导致当前状态被重复利用(例如完全背包问题),可以顺序遍历。
|
||||
|
||||
@ -2219,12 +2219,12 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
使用一维 dp 数组 `dp[j]` 表示「在当前考虑的物品下,背包容量为 j 时能够获得的最大价值」。
|
||||
|
||||
**2.确定递推公式**
|
||||
当考虑当前物品 i(重量为 weight[i],价值为 value[i])时,有两种选择:
|
||||
当考虑当前物品 `i` (重量为 `weight[i]`,价值为 `value[i]`)时,有两种选择:
|
||||
|
||||
- **不选当前物品 i:**
|
||||
此时的最大价值为 dp[j](即前面的状态没有变化)。
|
||||
此时的最大价值为 `dp[j]`(即前面的状态没有变化)。
|
||||
- **选当前物品 i:**
|
||||
当背包容量至少为 weight[i] 时,如果选择物品 i,剩余容量变为 j - weight[i],则最大价值为 dp[j - weight[i]] 加上 value[i]。
|
||||
当背包容量至少为 `weight[i]` 时,如果选择物品 `i` ,剩余容量变为 `j - weight[i]`,则最大价值为 `dp[j - weight[i]]` 加上 `value[i]`。
|
||||
|
||||
因此,状态转移方程为:
|
||||
$$
|
||||
@ -2234,7 +2234,7 @@ $$
|
||||
|
||||
`dp[0] = 0`,表示当背包容量为 0 时,能获得的最大价值自然为 0。
|
||||
|
||||
对于其他容量 dp[j],初始值也设为 0,dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。确保值不被初始值覆盖即可。
|
||||
对于其他容量 `dp[j]` ,初始值也设为 0,dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。确保值不被初始值覆盖即可。
|
||||
|
||||
**4.一维dp数组遍历顺序**
|
||||
|
||||
@ -2242,7 +2242,7 @@ $$
|
||||
|
||||
内层遍历背包容量(**逆序遍历**): 遍历容量从 capacity 到当前物品的重量,进行状态更新。
|
||||
|
||||
- 逆序遍历的目的在于确保当前物品在更新过程中只会被使用一次,因为 dp[j - weight[i]] 代表的是上一轮(当前物品未使用前)的状态,不会被当前物品更新后的状态覆盖。
|
||||
- 逆序遍历的目的在于确保当前物品在更新过程中只会被使用一次,因为 `dp[j - weight[i]]` 代表的是上一轮(当前物品未使用前)的状态,不会被当前物品更新后的状态覆盖。
|
||||
|
||||
|
||||
|
||||
@ -2308,7 +2308,7 @@ dp\[i][j] 表示从下标为[0-i]的物品,每个物品可以取无限次,
|
||||
**2. 确定递推公式**
|
||||
|
||||
- **不放物品i**:背包容量为j,里面不放物品i的最大价值是dp\[i - 1][j]。
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为j - weight[i],dp\[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp\[i][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为`j - weight[i]`,`dp[i][j - weight[i]]` 为背包容量为`j - weight[i]`且不放物品i的最大价值,那么`dp[i][j - weight[i]] + value[i]` (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
递推公式: `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);`
|
||||
|
||||
@ -2318,17 +2318,18 @@ dp\[i][j] 表示从下标为[0-i]的物品,每个物品可以取无限次,
|
||||
|
||||
```java
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 不选物品 i,价值不变
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
// 如果当前背包容量 j 能放下物品 i,则考虑选取物品 i(完全背包内层循环正序或逆序都可以,但这里通常建议正序)
|
||||
if (j >= weight[i]) {
|
||||
// 注意:这里选取物品 i 后仍然可以继续选取物品 i,
|
||||
// 所以状态转移方程为 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
|
||||
dp[i][j] = Math.max(dp[i][j], dp[i][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 不选物品 i,价值不变
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
// 如果当前背包容量 j 能放下物品 i,则考虑选取物品 i(完全背包内层循环正序或逆序都可以,但这里通常建议正序)
|
||||
if (j >= weight[i]) {
|
||||
// 注意:这里选取物品 i 后仍然可以继续选取物品 i,
|
||||
// 所以状态转移方程为 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
|
||||
dp[i][j] = Math.max(dp[i][j], dp[i][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
**3. dp数组如何初始化**
|
||||
@ -2338,13 +2339,13 @@ for (int i = 1; i < n; i++) {
|
||||
|
||||
```java
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 当 j 小于第 0 个物品重量时,无法选取,所以价值为 0
|
||||
if (j < weight[0]) {
|
||||
dp[0][j] = 0;
|
||||
} else {
|
||||
// 完全背包允许多次使用物品 0,所以递归地累加
|
||||
dp[0][j] = dp[0][j - weight[0]] + value[0];
|
||||
}
|
||||
// 当 j 小于第 0 个物品重量时,无法选取,所以价值为 0
|
||||
if (j < weight[0]) {
|
||||
dp[0][j] = 0;
|
||||
} else {
|
||||
// 完全背包允许多次使用物品 0,所以递归地累加
|
||||
dp[0][j] = dp[0][j - weight[0]] + value[0];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -2362,12 +2363,32 @@ for (int j = 0; j <= capacity; j++) {
|
||||
|
||||
压缩成一维,即`dp[j] = max(dp[j], dp[j - weight[i]] + value[i])`
|
||||
|
||||
- 根据题型选择先遍历物品或者背包,**如果求组合数就是外层for循环遍历物品,内层for遍历背包**。**如果求排列数就是外层for遍历背包,内层for循环遍历物品**。
|
||||
**组合不强调元素之间的顺序,排列强调元素之间的顺序**。
|
||||
- 根据题型选择先遍历物品或者背包,
|
||||
**如果求组合数就是外层for循环遍历物品,内层for遍历背包**。
|
||||
**如果求排列数就是外层for遍历背包,内层for循环遍历物品**。
|
||||
**组合数**(顺序不同的序列视为相同)**排列数**(顺序不同的序列视为不同)排列数大于等于组合数!!!。
|
||||
- 内层循环正序,不要逆序!因为要利用已经更新的dp数组,允许同一物品重复使用!
|
||||
|
||||
注意,完全背包和0/1背包的一维dp形式的递推公式一样,但是遍历顺序不同!!
|
||||
|
||||
```java
|
||||
public int completeKnapsack(int[] weight, int[] value, int capacity) {
|
||||
int n = weight.length;
|
||||
// dp[j] 表示容量为 j 时的最大价值,初始化为 0
|
||||
int[] dp = new int[capacity + 1];
|
||||
|
||||
// 遍历每件物品
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 完全背包:正序遍历容量
|
||||
for (int j = weight[i]; j <= capacity; j++) {
|
||||
// 如果拿 i 号物品,更新 dp[j]
|
||||
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
return dp[capacity];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 多重背包
|
||||
|
||||
152
杂项/mermaid画图.md
Normal file
152
杂项/mermaid画图.md
Normal file
@ -0,0 +1,152 @@
|
||||
# mermaid画图
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
A[多智能体随机网络结构分析] --> B[多智能体协同学习与推理]
|
||||
|
||||
A --> A1["谱参数实时估算"]
|
||||
A1 --> A11["卡尔曼滤波"]
|
||||
A1 --> A12["矩阵扰动理论"]
|
||||
A1 --> A13["输出:谱参数"]
|
||||
A --> A2["网络拓扑重构"]
|
||||
A2 --> A21["低秩分解重构"]
|
||||
A2 --> A22["聚类量化"]
|
||||
A2 --> A23["输出:邻接矩阵、特征矩阵"]
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
B[多智能体协同学习与推理]
|
||||
B --> B1["联邦学习、强化学习"]
|
||||
B1 --> B11["谱驱动学习率调整"]
|
||||
B1 --> B12["自适应节点选择策略"]
|
||||
B --> B2["动态图神经网络"]
|
||||
B2 --> B21["动态图卷积设计"]
|
||||
B2 --> B22["一致性推理"]
|
||||
```
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
%% 颜色和样式定义
|
||||
classDef startEnd fill:#e6ffe6,stroke:#333,stroke-width:2px
|
||||
classDef operation fill:#fff,stroke:#000,stroke-width:1px
|
||||
classDef decision fill:#ffcccc,stroke:#000,stroke-width:1px
|
||||
classDef update fill:#ccffcc,stroke:#000,stroke-width:1px
|
||||
|
||||
%% 节点定义(严格按图片顺序)
|
||||
A([开始]):::startEnd
|
||||
B[交易信息\n外部订单号]:::operation
|
||||
C{判断是否为锁单订单}:::decision
|
||||
D[查询拼团组队信息]:::operation
|
||||
E[更新订单详情\n状态为交易完成]:::update
|
||||
F[更新拼团组队进度]:::update
|
||||
G{拼团组队完结\n目标量判断}:::decision
|
||||
H[写入回调任务表]:::operation
|
||||
I([结束]):::startEnd
|
||||
|
||||
%% 流程连接(完全还原图片走向)
|
||||
A --> B
|
||||
B --> C
|
||||
C -->|是| D
|
||||
D --> E
|
||||
E --> F
|
||||
F --> G
|
||||
G -->|是| H
|
||||
H --> I
|
||||
C -->|否| I
|
||||
G -->|否| I
|
||||
|
||||
%% 保持原图连接线样式
|
||||
linkStyle 0,1,2,3,4,5,6,7,8 stroke-width:1px
|
||||
```
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
A[用户发起退单请求] --> B{检查拼团状态}
|
||||
|
||||
B -->|拼团未完成| C1[场景1:拼团中退单]
|
||||
C1 --> D1{是否已支付?}
|
||||
D1 -->|未支付| E1[取消订单]
|
||||
E1 --> F1[更新订单状态为2]
|
||||
F1 --> G1[通知拼团失败]
|
||||
G1 --> H1[退单完成]
|
||||
D1 -->|已支付| I1[发起退款]
|
||||
I1 --> F1
|
||||
|
||||
B -->|拼团已完成| C2[场景2:完成后退单]
|
||||
C2 --> D2{是否超时限?}
|
||||
D2 -->|未超时| E2[发起退款]
|
||||
E2 --> F2[更新订单状态]
|
||||
F2 --> H1
|
||||
D2 -->|超时| G2[退单失败]
|
||||
|
||||
style A fill:#f9f,stroke:#333
|
||||
style B fill:#66f,stroke:#333
|
||||
style C1 fill:#fbb,stroke:#f66
|
||||
style C2 fill:#9f9,stroke:#090
|
||||
|
||||
```
|
||||
|
||||
```mermaid
|
||||
flowchart LR
|
||||
%% ===================== 左侧:模板模式块 =====================
|
||||
subgraph Template["设计模式 - 模板"]
|
||||
direction TB
|
||||
SM["StrategyMapper
|
||||
策略映射器"]
|
||||
SH["StrategyHandler
|
||||
策略处理器"]
|
||||
ASR["AbstractStrategyRouter<T, D, R>
|
||||
策略路由抽象类"]
|
||||
|
||||
SM -->|实现| ASR
|
||||
SH -->|实现| ASR
|
||||
end
|
||||
|
||||
%% ===================== 右侧:策略工厂与支持类 =====================
|
||||
DASFactory["DefaultActivityStrategyFactory
|
||||
默认的拼团活动策略工厂"]
|
||||
AGMS["AbstractGroupBuyMarketSupport
|
||||
功能服务支撑类"]
|
||||
|
||||
DASFactory --> AGMS
|
||||
AGMS -->|继承| ASR
|
||||
|
||||
%% ===================== 业务节点链路 =====================
|
||||
Root["RootNode
|
||||
根节点"]
|
||||
Switch["SwitchRoot
|
||||
开关节点"]
|
||||
Market["MarketNode
|
||||
营销节点"]
|
||||
End["EndNode
|
||||
结尾节点"]
|
||||
Other["其他节点"]
|
||||
|
||||
AGMS --> Root
|
||||
Root --> Switch
|
||||
Switch --> Market
|
||||
Market --> End
|
||||
Switch -.-> Other
|
||||
Other --> End
|
||||
|
||||
%% ===================== 样式(可选) =====================
|
||||
classDef green fill:#DFF4E3,stroke:#3B7A57,stroke-width:1px;
|
||||
classDef red fill:#E74C3C,color:#fff,stroke:#B03A2E;
|
||||
classDef purple fill:#7E60A2,color:#fff,stroke:#4B3B6B;
|
||||
classDef blue fill:#3DA9F5,color:#fff,stroke:#1B6AA5;
|
||||
|
||||
class SM,SH,Root,Switch,Market,End,Other green;
|
||||
class DASFactory red;
|
||||
class AGMS purple;
|
||||
class ASR blue;
|
||||
|
||||
style Template stroke-dasharray: 5 5;
|
||||
|
||||
```
|
||||
|
||||
@ -1,32 +0,0 @@
|
||||
# mermaid画图
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
A[多智能体随机网络结构分析] --> B[多智能体协同学习与推理]
|
||||
|
||||
A --> A1["谱参数实时估算"]
|
||||
A1 --> A11["卡尔曼滤波"]
|
||||
A1 --> A12["矩阵扰动理论"]
|
||||
A1 --> A13["输出:谱参数"]
|
||||
A --> A2["网络拓扑重构"]
|
||||
A2 --> A21["低秩分解重构"]
|
||||
A2 --> A22["聚类量化"]
|
||||
A2 --> A23["输出:邻接矩阵、特征矩阵"]
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
```mermaid
|
||||
graph TD
|
||||
B[多智能体协同学习与推理]
|
||||
B --> B1["联邦学习、强化学习"]
|
||||
B1 --> B11["谱驱动学习率调整"]
|
||||
B1 --> B12["自适应节点选择策略"]
|
||||
B --> B2["动态图神经网络"]
|
||||
B2 --> B21["动态图卷积设计"]
|
||||
B2 --> B22["一致性推理"]
|
||||
```
|
||||
|
||||
177
项目/拼团交易系统.md
177
项目/拼团交易系统.md
@ -115,8 +115,6 @@ crowd_tags_job 人群标签任务
|
||||
| create_time | 创建时间 |
|
||||
| update_time | 更新时间 |
|
||||
|
||||
|
||||
|
||||
- 拼团活动表:设定了拼团的成团规则,人群标签的使用可以限定哪些人可见,哪些人可参与。
|
||||
- 折扣配置表:拆分出拼团优惠到一个新的表进行多条配置。如果折扣还有更多的复杂规则,则可以配置新的折扣规则表进行处理。
|
||||
- 人群标签表:专门来做人群设计记录的,这3张表就是为了把符合规则的人群ID,也就是用户ID,全部跑任务到一个记录下进行使用。比如黑玫瑰人群、高净值人群、拼团履约率90%以上的人群等。
|
||||
@ -313,7 +311,7 @@ EndNode.apply() → 组装结果并返回 TrialBalanceEntity
|
||||
|
||||
## 拼团结算
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/07/15/p876v1-0.png" alt="d56fcfb9708eb0d99600c751808bb843" style="zoom:80%;" />
|
||||
|
||||
|
||||
|
||||
|
||||
@ -376,6 +374,51 @@ EndNode.apply() → 组装结果并返回 TrialBalanceEntity
|
||||
|
||||
|
||||
|
||||
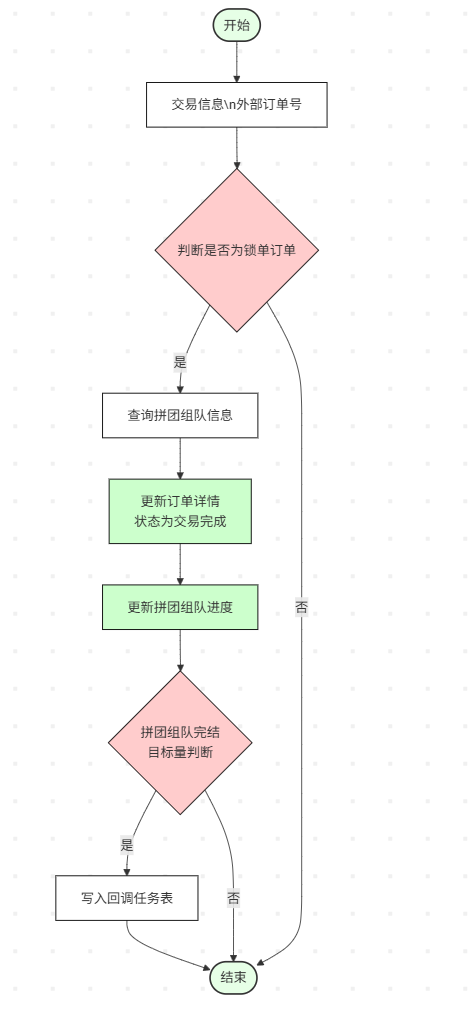
## 逆向工程:退单
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/07/25/hgggjo-0.png" alt="image-20250725105608390" style="zoom:67%;" />
|
||||
|
||||
逆向的流程,要分析用户是在哪个流程节点下进行中断行为。包括3个场景;
|
||||
|
||||
**已锁单、未支付**
|
||||
|
||||
- **用户行为**:完成锁单后未发起支付。
|
||||
- **结果**:订单超时自动关单。
|
||||
- 补偿
|
||||
- 若用户在临界时刻支付,则需执行“逆向退款”流程——退还支付金额并告知“优惠已过期,请重新参与”。
|
||||
- 否则该订单自动失效,释放拼团名额给后续用户。
|
||||
|
||||
**已锁单、已支付,但拼团未成团**
|
||||
|
||||
- **用户行为**:完成支付,组团人数不足暂未成团。
|
||||
|
||||
- 补偿策略
|
||||
|
||||
(可配置优先级):
|
||||
|
||||
1. **先退拼团,再退款,**
|
||||
2. **先退款,再退拼团**
|
||||
|
||||
- 具体执行哪种方式,可由拼团活动策略决定——“优先保障个人”或“优先保障成团”。
|
||||
|
||||
**已锁单、已支付,且拼团已成团**
|
||||
|
||||
- **用户行为**:支付成功,且组团人数已凑齐。
|
||||
- 补偿流程
|
||||
- 先退还用户支付金额;
|
||||
- 再撤销对应的拼团完成量。
|
||||
- **注意**:已成团订单视为“已完成含退单”,仍然成团、不再开放新用户参与,确保团队成团状态一致。
|
||||
|
||||
|
||||
|
||||
### 策略模板应用
|
||||
|
||||
根据订单状态和拼团状态动态选择退单策略。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 收获
|
||||
|
||||
### 实体对象
|
||||
@ -727,7 +770,7 @@ while 循环:
|
||||
|
||||
### 规则树流程
|
||||
|
||||
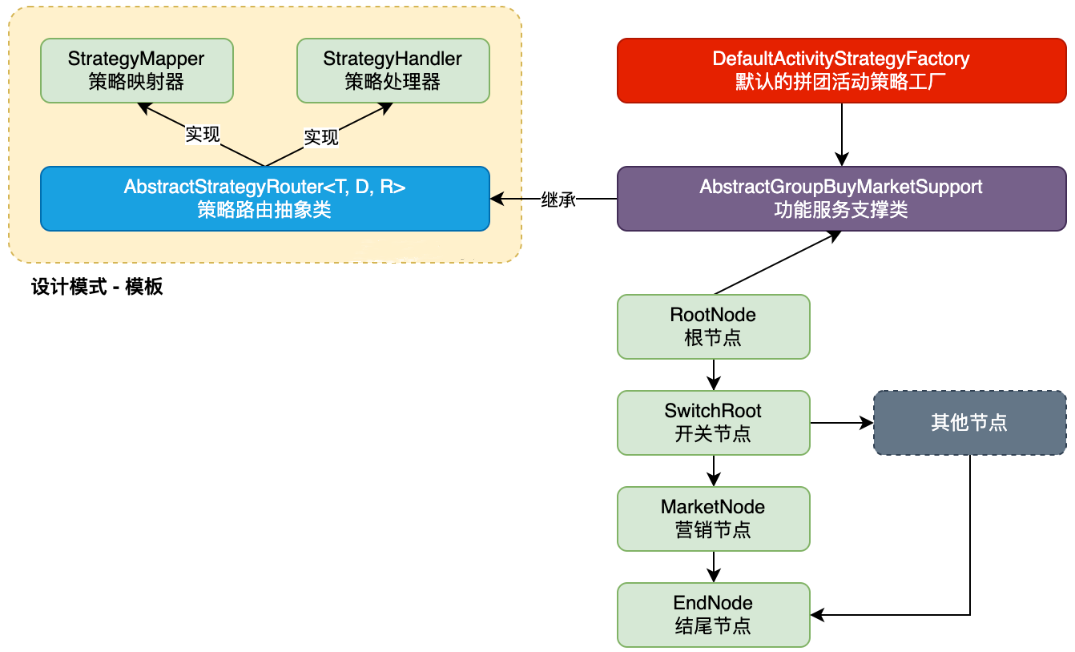
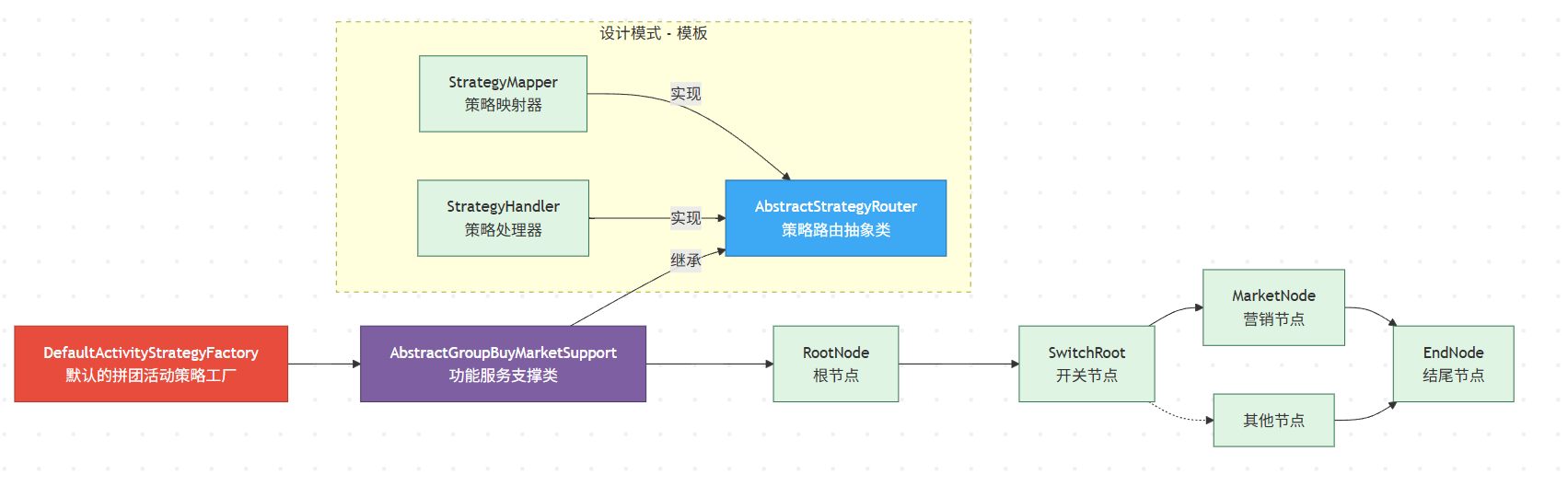
|
||||
!
|
||||
|
||||
**整体分层思路**
|
||||
|
||||
@ -814,10 +857,10 @@ private Map<String, IDiscountCalculateService> discountCalculateServiceMap;
|
||||
|
||||
**字段类型**:`Map<String, IDiscountCalculateService>`
|
||||
|
||||
- key—— Bean 的名字
|
||||
- key—— **Bean 的名字**
|
||||
- 默认是类名首字母小写 (`mjCalculateService`)
|
||||
- 或者你在实现类上显式写的 `@Service("MJ")`
|
||||
- **value** —— 那个实现类对应的实例
|
||||
- **value** —— 那个实现类对应的**实例**
|
||||
- **Spring 机制**:
|
||||
1. 启动时扫描所有实现 `IDiscountCalculateService` 的 Bean。
|
||||
2. 把它们按 “BeanName → Bean 实例” 的映射注入到这张 `Map` 里。
|
||||
@ -1624,3 +1667,125 @@ List<Product> list = getFromCacheOrDb(
|
||||
| 运维依赖 | **无**:不依赖外部组件 | **有**:需维护高可用的 Redis 集群,增加运维成本 |
|
||||
|
||||
目前本项目使用的是分布式限流,用Redisson
|
||||
|
||||
|
||||
|
||||
### 日志系统
|
||||
|
||||
#### 输出流向一览
|
||||
|
||||
输出到3个地方:控制台、本地文件、ELK日志(服务器上内存不足无法部署!)
|
||||
|
||||
| 日志级别 | 控制台 | 本地文件(异步) | Logstash (TCP) |
|
||||
| ----------- | ------ | ----------------------------- | -------------- |
|
||||
| TRACE/DEBUG | — | — | — |
|
||||
| INFO | ✔ | `log_info.log` | ✔ |
|
||||
| WARN | ✔ | `log_info.log``log_error.log` | ✔ |
|
||||
| ERROR/FATAL | ✔ | `log_info.log``log_error.log` | ✔ |
|
||||
|
||||
> 注意:实际写文件时,都是通过 ASYNC_FILE_INFO/ERROR 两个异步 Appender 执行,以免日志写盘阻塞业务线程。
|
||||
|
||||
#### ELK日志系统
|
||||
|
||||
本地文件每台机器都会在自己 `/data/log/...` 目录下滚动输出自己的日志,互相之间不会合并。
|
||||
|
||||
如果你希望跨多台服务器**统一管理**,就需要把日志推到中央端——ELK日志系统
|
||||
|
||||
ELK=Elasticsearch(存储&检索)+ Logstash(采集&处理)+ Kibana(可视化)
|
||||
|
||||
docker-compose.yml:
|
||||
|
||||
```yml
|
||||
version: '3'
|
||||
services:
|
||||
elasticsearch:
|
||||
image: elasticsearch:7.17.28
|
||||
ports: ['9201:9200','9300:9300']
|
||||
environment:
|
||||
- discovery.type=single-node
|
||||
- ES_JAVA_OPTS=-Xms512m -Xmx512m
|
||||
volumes:
|
||||
- ./data:/usr/share/elasticsearch/data
|
||||
logstash:
|
||||
image: logstash:7.17.28
|
||||
ports: ['4560:4560','9600:9600']
|
||||
volumes:
|
||||
- ./logstash/logstash.conf:/usr/share/logstash/pipeline/logstash.conf
|
||||
environment:
|
||||
- LS_JAVA_OPTS=-Xms1g -Xmx1g
|
||||
kibana:
|
||||
image: kibana:7.17.28
|
||||
ports: ['5601:5601']
|
||||
environment:
|
||||
- elasticsearch.hosts=http://elasticsearch:9200
|
||||
networks:
|
||||
default:
|
||||
driver: bridge
|
||||
|
||||
```
|
||||
|
||||
kibana配置:
|
||||
|
||||
```yml
|
||||
#
|
||||
# ** THIS IS AN AUTO-GENERATED FILE **
|
||||
#
|
||||
|
||||
# Default Kibana configuration for docker target
|
||||
server.host: "0"
|
||||
server.shutdownTimeout: "5s"
|
||||
elasticsearch.hosts: [ "http://elasticsearch:9200" ] # 记得修改ip
|
||||
monitoring.ui.container.elasticsearch.enabled: true
|
||||
i18n.locale: "zh-CN"
|
||||
```
|
||||
|
||||
logstash配置:
|
||||
|
||||
```conf
|
||||
input {
|
||||
tcp {
|
||||
mode => "server"
|
||||
host => "0.0.0.0"
|
||||
port => 4560
|
||||
codec => json_lines
|
||||
type => "info"
|
||||
}
|
||||
}
|
||||
filter {}
|
||||
output {
|
||||
elasticsearch {
|
||||
action => "index"
|
||||
hosts => "es:9200"
|
||||
index => "group-buy-market-log-%{+YYYY.MM.dd}"
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
自己的项目:
|
||||
|
||||
```java
|
||||
<!-- 上报日志;ELK -->
|
||||
<springProperty name="LOG_STASH_HOST" scope="context" source="logstash.host" defaultValue="127.0.0.1"/>
|
||||
|
||||
<!--输出到logstash的appender-->
|
||||
<appender name="LOGSTASH" class="net.logstash.logback.appender.LogstashTcpSocketAppender">
|
||||
<!--可以访问的logstash日志收集端口-->
|
||||
<destination>${LOG_STASH_HOST}:4560</destination>
|
||||
<encoder charset="UTF-8" class="net.logstash.logback.encoder.LogstashEncoder"/>
|
||||
</appender>
|
||||
```
|
||||
|
||||
```xml
|
||||
<dependency>
|
||||
<groupId>net.logstash.logback</groupId>
|
||||
<artifactId>logstash-logback-encoder</artifactId>
|
||||
<version>7.3</version>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
**使用**
|
||||
|
||||
检查索引:curl http://localhost:9201/_cat/indices?v3
|
||||
|
||||
打开 Kibana:浏览器访问 `http://localhost:5601`,新建 索引模式(如 `app-log-*`),即可在 Discover/Visualize 中查看与分析日志。
|
||||
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user