Commit on 2025/04/23 周三 11:37:25.96
This commit is contained in:
parent
1e65bba5d3
commit
65fc5aa440
3
科研/zy.md
Normal file
3
科研/zy.md
Normal file
@ -0,0 +1,3 @@
|
||||
如何确定kmeans的簇数?节点之间的流量,空间转为时间的图。
|
||||
|
||||
压缩感知 函数拟合 采样定理 傅里叶变换
|
||||
154
科研/卡尔曼滤波.md
154
科研/卡尔曼滤波.md
@ -100,7 +100,11 @@ $$
|
||||
|
||||
# 扩展卡尔曼滤波
|
||||
|
||||
扩展卡尔曼滤波(Extended Kalman Filter,简称 EKF)是一种针对非线性系统状态估计问题的滤波方法。传统的卡尔曼滤波要求系统的状态转移和观测模型都是线性的,而在实际问题中,很多系统往往存在非线性特性。EKF 的核心思想就是对非线性模型进行局部线性化,然后在此基础上应用卡尔曼滤波的递归估计方法。
|
||||
扩展卡尔曼滤波(Extended Kalman Filter,简称 EKF)是一种针对非线性系统状态估计问题的滤波方法。传统的卡尔曼滤波要求系统的状态转移和观测模型都是线性的,而在实际问题中,很多系统往往存在非线性特性。
|
||||
|
||||
EKF 的核心思想就是对非线性模型进行**局部线性化**,然后在线性化后的模型上**直接套用标准卡尔曼滤波(KF)的预测和更新公式**。
|
||||
|
||||
|
||||
|
||||
1. **非线性系统模型**
|
||||
假设系统的状态转移和观测模型为非线性的:
|
||||
@ -250,3 +254,151 @@ H = \begin{bmatrix}
|
||||
0 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
|
||||
# 无迹卡尔曼(UKF)
|
||||
|
||||
#### UKF 具体步骤(分步解析)
|
||||
|
||||
| 符号 | 含义 | 维度 |
|
||||
| ------------------------- | ------------------------------ | ------------------- |
|
||||
| $ \mathbf{x} $ | 系统状态向量 | $ n \times 1 $ |
|
||||
| $ P $ | 状态协方差矩阵 | $ n \times n $ |
|
||||
| $ \mathbf{z} $ | 观测向量 | $ m \times 1 $ |
|
||||
| $ f(\cdot) $ | 非线性状态转移函数 | - |
|
||||
| $ h(\cdot) $ | 非线性观测函数 | - |
|
||||
| $ Q $ | 过程噪声协方差 | $ n \times n $ |
|
||||
| $ R $ | 观测噪声协方差 | $ m \times m $ |
|
||||
| $ \mathcal{X} $ | Sigma点集合 | $ n \times (2n+1) $ |
|
||||
| $ W^{(m)} $ | 均值权重 | $ 1 \times (2n+1) $ |
|
||||
| $ W^{(c)} $ | 协方差权重 | $ 1 \times (2n+1) $ |
|
||||
| $ \alpha, \beta, \kappa $ | UKF调参参数(控制Sigma点分布) | 标量 |
|
||||
|
||||
**Step 1: 生成Sigma点(确定性采样)**
|
||||
|
||||
**目的**:根据当前状态均值和协方差,生成一组代表状态分布的采样点。
|
||||
**公式**:
|
||||
$$
|
||||
\begin{aligned}
|
||||
\mathcal{X}_0 &= \hat{\mathbf{x}}_{k-1|k-1} \\
|
||||
\mathcal{X}_i &= \hat{\mathbf{x}}_{k-1|k-1} + \left( \sqrt{(n+\lambda) P_{k-1|k-1}} \right)_i \quad (i=1,\dots,n) \\
|
||||
\mathcal{X}_{i+n} &= \hat{\mathbf{x}}_{k-1|k-1} - \left( \sqrt{(n+\lambda) P_{k-1|k-1}} \right)_i \quad (i=1,\dots,n)
|
||||
\end{aligned}
|
||||
$$
|
||||
**符号说明**:
|
||||
|
||||
- $ \sqrt{(n+\lambda) P} $:协方差矩阵的平方根(如Cholesky分解)。
|
||||
- $ \left( \sqrt{(n+\lambda) P} \right)_i $ 表示平方根矩阵的第 $ i $ 列。
|
||||
- $ \lambda = \alpha^2 (n + \kappa) - n $:缩放因子($ \alpha $控制分布范围,通常取1e-3;$ \kappa $通常取0)。
|
||||
- **为什么是 $ 2n+1 $ 个点**?1个中心点 + $ 2n $个对称点,覆盖状态空间的主要方向。
|
||||
|
||||
**示例:**
|
||||
|
||||
假设状态 $ \mathbf{x} = [x, y]^T $,$ n = 2 $,$ P = \begin{bmatrix} 4 & 0 \\ 0 & 1 \end{bmatrix} $,$ \lambda = 0 $:
|
||||
|
||||
1. **计算平方根矩阵**(Cholesky分解):
|
||||
$$
|
||||
\sqrt{(n+\lambda) P} = \sqrt{2} \cdot \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2.828 & 0 \\ 0 & 1.414 \end{bmatrix}
|
||||
$$
|
||||
|
||||
2. **生成 Sigma 点**:
|
||||
$$
|
||||
\begin{aligned}
|
||||
\mathcal{X}_0 &= \hat{\mathbf{x}} \\
|
||||
\mathcal{X}_1 &= \hat{\mathbf{x}} + [2.828, 0]^T = [\hat{x} + 2.828, \hat{y}] \\
|
||||
\mathcal{X}_2 &= \hat{\mathbf{x}} + [0, 1.414]^T = [\hat{x}, \hat{y} + 1.414] \\
|
||||
\mathcal{X}_3 &= \hat{\mathbf{x}} - [2.828, 0]^T = [\hat{x} - 2.828, \hat{y}] \\
|
||||
\mathcal{X}_4 &= \hat{\mathbf{x}} - [0, 1.414]^T = [\hat{x}, \hat{y} - 1.414] \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
**Step 2: 计算Sigma点权重**
|
||||
|
||||
**目的**:为每个Sigma点分配权重,用于后续计算均值和协方差。
|
||||
**公式**:
|
||||
$$
|
||||
\begin{aligned}
|
||||
W_0^{(m)} &= \frac{\lambda}{n + \lambda} \quad &\text{(中心点均值权重)} \\
|
||||
W_0^{(c)} &= \frac{\lambda}{n + \lambda} + (1 - \alpha^2 + \beta) \quad &\text{(中心点协方差权重)} \\
|
||||
W_i^{(m)} = W_i^{(c)} &= \frac{1}{2(n + \lambda)} \quad (i=1,\dots,2n) \quad &\text{(对称点权重)}
|
||||
\end{aligned}
|
||||
$$
|
||||
**符号说明**:
|
||||
|
||||
- $ \beta $:高阶矩调节参数(高斯分布时取2最优)。
|
||||
- **权重作用**:中心点通常权重较大,对称点权重均等。
|
||||
|
||||
---
|
||||
|
||||
**Step 3: 预测步骤(时间更新)**
|
||||
|
||||
**目的**:将Sigma点通过非线性状态方程传播,计算预测状态和协方差。
|
||||
**子步骤**:
|
||||
|
||||
1. **传播Sigma点**:
|
||||
$$
|
||||
\mathcal{X}_{i,k|k-1}^* = f(\mathcal{X}_{i,k-1}, \mathbf{u}_{k-1}), \quad i=0,1,...,2n
|
||||
$$
|
||||
(每个Sigma点独立通过 $ f(\cdot) $ 计算)
|
||||
|
||||
2. **计算预测均值和协方差**:
|
||||
$$
|
||||
\hat{\mathbf{x}}_{k|k-1} = \sum_{i=0}^{2n} W_i^{(m)} \mathcal{X}_{i,k|k-1}^*
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{k|k-1} = \sum_{i=0}^{2n} W_i^{(c)} \left( \mathcal{X}_{i,k|k-1}^* - \hat{\mathbf{x}}_{k|k-1} \right) \left( \mathcal{X}_{i,k|k-1}^* - \hat{\mathbf{x}}_{k|k-1} \right)^T + Q_k
|
||||
$$
|
||||
|
||||
**符号说明**:
|
||||
|
||||
- $\mathcal{X}_{k-1}$:上一时刻生成的Sigma点集合($2n+1$个点)
|
||||
- $\mathcal{X}_{k|k-1}^*$:通过状态方程传播后的Sigma点集合
|
||||
|
||||
- $ Q_k $:过程噪声(表示模型不确定性)。
|
||||
|
||||
---
|
||||
|
||||
**Step 4: 观测更新(测量更新)**
|
||||
|
||||
**目的**:将预测的Sigma点通过观测方程传播,计算卡尔曼增益并更新状态。
|
||||
**子步骤**:
|
||||
|
||||
1. **生成观测Sigma点**:
|
||||
$$
|
||||
\mathcal{Z}_{i,k|k-1} = h(\mathcal{X}_{i,k|k-1}^*), \quad i=0,...,2n
|
||||
$$
|
||||
|
||||
2. **计算观测预测统计量**:
|
||||
$$
|
||||
\hat{\mathbf{z}}_{k|k-1} = \sum_{i=0}^{2n} W_i^{(m)} \mathcal{Z}_{i,k|k-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{z_k z_k} = \sum_{i=0}^{2n} W_i^{(c)} \left( \mathcal{Z}_{i,k|k-1} - \hat{\mathbf{z}}_{k|k-1} \right) \left( \mathcal{Z}_{i,k|k-1} - \hat{\mathbf{z}}_{k|k-1} \right)^T + R_k
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{x_k z_k} = \sum_{i=0}^{2n} W_i^{(c)} \left( \mathcal{X}_{i,k|k-1}^* - \hat{\mathbf{x}}_{k|k-1} \right) \left( \mathcal{Z}_{i,k|k-1} - \hat{\mathbf{z}}_{k|k-1} \right)^T
|
||||
$$
|
||||
|
||||
**符号说明**:
|
||||
|
||||
- $ P_{z_k z_k} $:观测自协方差(含噪声 $ R_k $)。
|
||||
- $ P_{x_k z_k} $:状态-观测互协方差。
|
||||
|
||||
3. **计算卡尔曼增益和更新状态**:
|
||||
$$
|
||||
K_k = P_{x_k z_k} P_{z_k z_k}^{-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\hat{\mathbf{x}}_{k|k} = \hat{\mathbf{x}}_{k|k-1} + K_k (\mathbf{z}_k - \hat{\mathbf{z}}_{k|k-1})
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{k|k} = P_{k|k-1} - K_k P_{z_k z_k} K_k^T
|
||||
$$
|
||||
|
||||
|
||||
89
科研/数学基础.md
89
科研/数学基础.md
@ -556,6 +556,49 @@ w = L @ Z # 等价于 np.dot(L, Z)
|
||||
|
||||
|
||||
|
||||
## 概率密度函数
|
||||
|
||||
**定义**:
|
||||
概率密度函数是描述**连续型随机变量**在某个取值点附近的可能性"密度"的函数。注意:
|
||||
|
||||
- PDF在某一点的值**不是概率**,而是概率的"密度"。
|
||||
- 实际概率是通过对PDF在某个区间内**积分**得到的(比如 $P(a \leq X \leq b) = \int_a^b f(x)dx$)。
|
||||
- PDF的**全域积分**必须等于1(即所有可能性的总和为100%)。
|
||||
|
||||
**例子**:
|
||||
假设某人的每日通勤时间 $X$ 是一个连续随机变量,其PDF可能是一个钟形曲线(如正态分布)。PDF在 $x=30$ 分钟处的值 $f(30)$ 表示"30分钟附近"的概率密度,而 $P(25 \leq X \leq 35)=0.4$ 表示约有40%的概率通勤时间会落在这个区间。
|
||||
|
||||
|
||||
|
||||
## 指数分布
|
||||
|
||||
**定义**:
|
||||
指数分布是一种常见的**连续型概率分布**,通常用于描述"事件间隔时间"或"无记忆性"的过程。比如:
|
||||
|
||||
- 客服电话的间隔时间。
|
||||
- 灯泡的寿命。
|
||||
- 地震发生的间隔时间。
|
||||
|
||||
**概率密度函数(PDF)**:
|
||||
指数分布的PDF公式为:
|
||||
$$
|
||||
f(x) = \lambda e^{-\lambda x} \quad (x \geq 0)
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $\lambda$ 是**率参数**(单位时间内事件发生的平均次数)。
|
||||
- $1/\lambda$ 是事件的**平均间隔时间**。
|
||||
|
||||
**无记忆性**:已经等待了时间 $t$,再等待额外时间 $s$ 的概率与从头开始等待 $s$ 的概率相同(即 $P(X > t+s \mid X > t) = P(X > s)$)。
|
||||
|
||||
**例子**:
|
||||
假设某网站用户访问的间隔时间服从 $\lambda = 0.5$(平均每2分钟1次访问),则:
|
||||
|
||||
- PDF为 $f(x) = 0.5 e^{-0.5x}$。
|
||||
- 用户在接下来1分钟内访问的概率是 $P(0 \leq X \leq 1) = \int_0^1 0.5 e^{-0.5x} dx \approx 0.393$。
|
||||
|
||||
|
||||
|
||||
## 高斯分布
|
||||
|
||||
高斯分布的概率密度函数:
|
||||
@ -625,14 +668,14 @@ $$
|
||||
|
||||
### **拉普拉斯矩阵及其性质**
|
||||
|
||||
对于一个无向图 \(G = (V, E)\),其拉普拉斯矩阵 \(L\) 通常定义为
|
||||
对于一个无向图 $G = (V, E)$,其拉普拉斯矩阵 $L$ 通常定义为
|
||||
$$
|
||||
L = D - A,
|
||||
$$
|
||||
其中:
|
||||
|
||||
- \(D\) 是度矩阵,一个对角矩阵,其对角元 \($d_i$\) 为顶点 \(i\) 的度数;
|
||||
- \(A\) 是邻接矩阵,反映了图中各顶点之间的连接关系。
|
||||
- $D$是度矩阵,一个对角矩阵,其对角元 \($d_i$\) 为顶点 $i$ 的度数;
|
||||
- $A$是邻接矩阵,反映了图中各顶点之间的连接关系。
|
||||
|
||||
示例:
|
||||
考虑一个简单的无向图,该图包含三个顶点:1, 2, 3,以及两条边: - 边 (1, 2) - 边 (2, 3)
|
||||
@ -709,21 +752,21 @@ L\mathbf{1} = \begin{pmatrix}
|
||||
\end{pmatrix}.
|
||||
$$
|
||||
|
||||
这说明常数向量 \($\mathbf{1}$\) 是 \(L\) 的零空间中的一个向量,即零特征值对应的特征向量。
|
||||
这说明常数向量 $\mathbf{1}$ 是 $L$ 的零空间中的一个向量,即零特征值对应的特征向量。
|
||||
|
||||
**主要性质**
|
||||
|
||||
1. 对称性
|
||||
|
||||
由于对于无向图,邻接矩阵 \(A\) 是对称的,而度矩阵 \(D\) 本身也是对称的(因为它是对角矩阵),所以拉普拉斯矩阵 \(L\) 也是对称矩阵。
|
||||
由于对于无向图,邻接矩阵 \(A\) 是对称的,而度矩阵 \(D\) 本身也是对称的(因为它是对角矩阵),所以拉普拉斯矩阵 $L$ 也是对称矩阵。
|
||||
|
||||
2. 正半定性
|
||||
|
||||
对于任意实向量 \(x\),都有:
|
||||
对于任意实向量 $x$,都有:
|
||||
$$
|
||||
x^T L x = \sum_{(i,j) \in E} (x_i - x_j)^2 \ge 0.
|
||||
$$
|
||||
这说明 \(L\) 是正半定矩阵,即其所有特征值均非负。
|
||||
这说明 $L$ 是正半定矩阵,即其所有特征值均非负。
|
||||
|
||||
3. 零特征值与连通分量
|
||||
|
||||
@ -736,7 +779,7 @@ $$
|
||||
其中 $\mathbf{1} = (1, 1, \ldots, 1)^T$,因此 $0$ 一定是 $L$ 的一个特征值。
|
||||
因为拉普拉斯矩阵的定义为 $L = D - A$,其中每一行的元素之和为零,所以当向量所有分量都相等时,每一行的加权求和自然等于零。
|
||||
|
||||
- 更进一步,**零特征值的重数等于图的连通分量(独立的子图)个数**。也就是说,如果图 \(G\) 有 \(k\) 个连通分量,则 \(L\) 的零特征值重数为 \(k\)。
|
||||
- 更进一步,**零特征值的重数等于图的连通分量(独立的子图)个数**。也就是说,如果图 $G$ 有 $k$ 个连通分量,则 $L$ 的零特征值重数为 $k$ 。
|
||||
|
||||
**简单证明思路**
|
||||
|
||||
@ -744,7 +787,7 @@ $$
|
||||
|
||||
4. **谱分解及应用**
|
||||
|
||||
由于 \(L\) 是对称正半定矩阵,其可以进行谱分解:
|
||||
由于 $L$ 是对称正半定矩阵,其可以进行谱分解:
|
||||
$$
|
||||
L = U \Lambda U^T,
|
||||
$$
|
||||
@ -1174,8 +1217,34 @@ $$
|
||||
|
||||
- 归一化向量 ≈ 主特征向量
|
||||
|
||||
- 特征值估计:
|
||||
- 特征值估计(瑞利商(Rayleigh Quotient)):
|
||||
$$
|
||||
\lambda^{(k)} = \frac{(x^{(k)})^T A x^{(k)}}{(x^{(k)})^T x^{(k)}}
|
||||
$$
|
||||
|
||||
**瑞利商(Rayleigh Quotient)推导:**
|
||||
|
||||
假设 $x$ 是 $A$ 的一个近似特征向量(比如幂迭代法得到的 $x^{(k)}$),我们希望找到一个标量 $\lambda$ 使得 $A x \approx \lambda x$。
|
||||
|
||||
为了找到最优的 $\lambda$,可以最小化残差 $\| A x - \lambda x \|^2$:
|
||||
$$
|
||||
\| A x - \lambda x \|^2 = (A x - \lambda x)^T (A x - \lambda x)
|
||||
$$
|
||||
展开后:
|
||||
$$
|
||||
= x^T A^T A x - 2 \lambda x^T A x + \lambda^2 x^T x
|
||||
$$
|
||||
|
||||
对 $\lambda$ 求导并令导数为零:
|
||||
$$
|
||||
\frac{d}{d\lambda} \| A x - \lambda x \|^2 = -2 x^T A x + 2 \lambda x^T x = 0
|
||||
$$
|
||||
解得:
|
||||
$$
|
||||
\lambda = \frac{x^T A x}{x^T x}
|
||||
$$
|
||||
这就是 **瑞利商** 的表达式:
|
||||
$$
|
||||
\lambda^{(k)} = \frac{(x^{(k)})^T A x^{(k)}}{(x^{(k)})^T x^{(k)}}
|
||||
$$
|
||||
|
||||
|
||||
48
科研/线性代数.md
48
科研/线性代数.md
@ -828,6 +828,54 @@ $$
|
||||
|
||||
|
||||
|
||||
## 正定\正半定矩阵
|
||||
|
||||
1. **正定矩阵(PD)**
|
||||
$$
|
||||
A \text{ 正定} \iff \forall\, x \in \mathbb{R}^n \setminus \{0\}, \quad x^T A x > 0.
|
||||
$$
|
||||
|
||||
2. **正半定矩阵(PSD)**
|
||||
$$
|
||||
A \text{ 正半定} \iff \forall\, x \in \mathbb{R}^n, \quad x^T A x \ge 0.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
- **PD**:所有特征值都严格大于零。
|
||||
$\lambda_i(A)>0,\;i=1,\dots,n$。
|
||||
|
||||
- **PSD**:所有特征值都非负。
|
||||
$\lambda_i(A)\ge0,\;i=1,\dots,n$。
|
||||
|
||||
|
||||
|
||||
**拉普拉斯矩阵是正半定矩阵!**
|
||||
|
||||
对于任意实矩阵 $A$(大小为 $m\times n$),矩阵 $B = A^T A\quad(\text{大小为 }n\times n).$是半正定矩阵
|
||||
|
||||
- 显然
|
||||
$$
|
||||
B^T = (A^T A)^T = A^T (A^T)^T = A^T A = B,
|
||||
$$
|
||||
所以 $B$ 是对称矩阵。
|
||||
|
||||
- 对任意向量 $x\in\mathbb R^n$,有
|
||||
$$
|
||||
x^T B\,x = x^T (A^T A) x = (Ax)^T (Ax) = \|Ax\|^2 \;\ge\;0.
|
||||
$$
|
||||
因此 $B$ 总是 **正半定(PSD)** 的。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 对称非负矩阵分解
|
||||
|
||||
$$
|
||||
|
||||
35
科研/草稿.md
35
科研/草稿.md
@ -1 +1,34 @@
|
||||
压缩感知 函数拟合 采样定理 傅里叶变换
|
||||
您发现了符号不一致的问题!确实,这里需要统一符号表示。根据论文和您之前的笔记,正确的对应关系如下:
|
||||
|
||||
---
|
||||
|
||||
### **修正后的公式**
|
||||
1. **瑞利商计算**(对应论文式4-51):
|
||||
- 所有节点交换的是**本地滤波结果** $\hat{b}_{i,k|k}$(即UKF更新后的状态估计值),而非中间变量$b_i(k)$。
|
||||
- 正确的全局状态计算应为:
|
||||
$$
|
||||
y(k) = \frac{\sum_{i=1}^N x_i(k) \hat{b}_{i,k|k}}{\sum_{i=1}^N x_i^2(k)}
|
||||
$$
|
||||
- **物理意义**:$x_i(k)$是节点$i$的状态分量(用于正交化),$\hat{b}_{i,k|k}$是UKF更新的本地估计值。
|
||||
|
||||
2. **正交化**(对应论文式4-52):
|
||||
- 更新的是**状态分量** $x_i(k+1)$,其归一化分母应为所有节点的$\hat{b}_{i,k|k}$的2-范数:
|
||||
$$
|
||||
x_i(k+1) = \frac{\hat{b}_{i,k|k}}{\|\hat{b}(k)\|_2}, \quad \text{其中} \quad \|\hat{b}(k)\|_2 = \sqrt{\sum_{i=1}^N \hat{b}_{i,k|k}^2}
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### **符号一致性说明**
|
||||
- **$\hat{b}_{i,k|k}$**:节点$i$在时刻$k$的UKF后验估计值(即滤波结果)。
|
||||
- **$x_i(k)$**:节点$i$的状态分量(用于分布式正交化,与$\hat{b}_{i,k|k}$同步更新)。
|
||||
- **$b_i(k)$**:在论文中可能被用作中间变量(如式4-40的幂迭代状态),但最终滤波输出统一为$\hat{b}_{i,k|k}$。
|
||||
|
||||
---
|
||||
|
||||
### **修正后的流程**
|
||||
1. **UKF更新**:每个节点计算$\hat{b}_{i,k|k}$(原笔记Step 4输出)。
|
||||
2. **一致性协议**:节点交换$\hat{b}_{i,k|k}$,计算瑞利商$y(k)$。
|
||||
3. **正交化**:用$\hat{b}_{i,k|k}$更新$x_i(k+1)$,确保状态分量正交性。
|
||||
|
||||
这样既符合论文的分布式滤波逻辑,又保持了符号一致性。是否需要进一步解释某一步骤?
|
||||
635
科研/陈茂森论文.md
635
科研/陈茂森论文.md
@ -4,7 +4,7 @@
|
||||
|
||||
### 马尔科夫链与网络平均度推导
|
||||
|
||||
**1.马尔科夫链的基本概念**
|
||||
#### **1.马尔科夫链的基本概念**
|
||||
|
||||
马尔科夫链描述的是这样一种随机过程:系统在若干个可能的状态中变化,**下一时刻所处状态只依赖于当前状态**,而与过去的状态无关,这就是所谓的“无记忆性”或**马尔科夫性**。
|
||||
|
||||
@ -15,26 +15,37 @@ $$
|
||||
|
||||
假设你已经等待了 $s$ 分钟,那么再等待至少 $t$ 分钟的概率,和你一开始就等待至少 $t$ 分钟的概率完全相同。
|
||||
|
||||
|
||||
|
||||
在这个模型中,每条链路只有两个可能的状态:
|
||||
|
||||
- **状态0**:链路断开
|
||||
- **状态1**:链路连通
|
||||
|
||||
设在时刻 $t$ 时,某条链路处于连通状态的概率为 $p_1(t)$;由于只有两种状态,所以断开的概率就是
|
||||
在所有概率分布里,只有指数分布
|
||||
$$
|
||||
p_0(t)=1-p_1(t).
|
||||
P(T>t) = e^{-\lambda t}
|
||||
$$
|
||||
具有这种“无记忆性”特征:
|
||||
|
||||
$$
|
||||
P(T>s+t \mid T>s) = \frac{P(T>s+t)}{P(T>s)} = \frac{e^{-\lambda(s+t)}}{e^{-\lambda s}} = e^{-\lambda t} = P(T>t).
|
||||
$$
|
||||
|
||||
同时,我们假设链路从一个状态转移到另一个状态需要等待一段时间,这段**等待时间**通常服从**指数分布**(论文中通过 KS 检验确认)。这意味着,从0到1和从1到0有两个转移速率,我们记作:
|
||||
|
||||
- 从0到1的转移速率为 $\lambda_{01}$
|
||||
- 从1到0的转移速率为 $\lambda_{10}$
|
||||
#### **链路状态的马尔科夫模型**
|
||||
|
||||
这些速率表示单位时间内发生状态转换的可能性。
|
||||
考虑网络中每条链路的动态行为,其状态空间为:
|
||||
|
||||
**2.推导单条链路的连通概率**
|
||||
- **状态0**:链路断开
|
||||
- **状态1**:链路连通
|
||||
|
||||
**定义概率函数**:
|
||||
|
||||
- $p_1(t)$:时刻 $t$ 处于连通状态的概率
|
||||
- $p_0(t) = 1 - p_1(t)$:断开概率
|
||||
|
||||
同时,我们假设链路从一个状态转移到另一个状态需要等待一段时间,这段**等待时间**通常服从**指数分布**(论文中通过 KS 检验确认):
|
||||
|
||||
- 从断开(0)到连通(1)的等待时间 $T_{01} \sim \text{Exp}(\lambda_{01})$
|
||||
- 从连通(1)到断开(0)的等待时间 $T_{10} \sim \text{Exp}(\lambda_{10})$
|
||||
|
||||
其中,$\lambda_{01}$ 和 $\lambda_{10}$ 为转移速率,表示单位时间内事件(转移)发生的**平均次数**
|
||||
|
||||
#### **2.推导单条链路的连通概率**
|
||||
|
||||
根据连续时间马尔科夫链的理论,我们可以写出**状态转移的微分方程**。对于状态1(连通状态),概率 $p_1(t)$ 的变化率由两个部分组成:
|
||||
|
||||
@ -60,7 +71,7 @@ $$
|
||||
|
||||
这其实是一个一阶线性微分方程,其标准求解方法是求解其齐次解与非齐次解。
|
||||
|
||||
**3. 求解微分方程**
|
||||
#### **3. 求解微分方程**
|
||||
|
||||
整个微分方程的通解为:
|
||||
$$
|
||||
@ -81,7 +92,7 @@ $$
|
||||
|
||||
这就是单条链路的连通概率函数,描述了从任意初始条件出发,经过一段时间后,链路达到平衡状态的过程。
|
||||
|
||||
**4.推导网络平均度的变化函数**
|
||||
#### **4.推导网络平均度的变化函数**
|
||||
|
||||
在一个由 $N$ 个节点构成的网络中,每个节点都与其它节点进行通信(不考虑自环),因此每个节点最多有 $N-1$ 个邻居。对于任意一对节点 $i$ 和 $j$,它们之间链路连通的概率 $p_1(t)$(假设所有链路**独立且同分布**)。
|
||||
|
||||
@ -183,35 +194,577 @@ $$
|
||||
|
||||
### 系统稳定性分析
|
||||
|
||||
**建立系统状态方程与平衡点**
|
||||
|
||||
论文将随机移动网络的动态演化描述为一个一般的状态方程:
|
||||
#### 平衡点及误差坐标
|
||||
|
||||
论文第 2.1 节推导出,单条链路连通概率 $p_1(t)$ 满足
|
||||
$$
|
||||
\frac{dx}{dt} = f(x, t)
|
||||
\dot p_1(t)
|
||||
= -(\lambda_{01}+\lambda_{10})\,p_1(t) \;+\;\lambda_{01}.
|
||||
\tag{2‑18}
|
||||
$$
|
||||
其中,$x$ 是系统的 $n$ 维状态向量,$f(x, t)$ 是描述状态随时间变化的函数。
|
||||
|
||||
- **平衡点定义**: 当存在一个状态 $x_e$ 满足对任意 $t$,有
|
||||
$f(x_e, t) = 0$
|
||||
这时 $x_e$ 就是系统的平衡状态。如论文中特别关注的网络平均度 $x_d$,不再随时间变化。
|
||||
|
||||
**采用李雅普诺夫第二类方法**
|
||||
|
||||
由于本系统状态向量各分量间关系复杂,且无法求出状态矩阵的全部特征值,所以不能采用第一类方法。因此选择构造“李雅普诺夫函数”(第二类方法)来验证系统的稳定性。
|
||||
|
||||
**构造李雅普诺夫函数**
|
||||
网络有 $N$ 个节点,**平均度**
|
||||
$$
|
||||
V(x) = (x - x_e)^T P (x - x_e)
|
||||
d(t) = (N-1)\,p_1(t).
|
||||
$$
|
||||
其中 $P$ 是一个正定矩阵。由此保证:
|
||||
|
||||
- **正定性**: 对于除 $x = x_e$ 外的所有状态,$V(x) > 0$;且在平衡点 $x_e$ 处有 $V(x_e) = 0$。
|
||||
|
||||
**分析李雅普诺夫函数的时间导数**
|
||||
设平衡连通概率 $p_1^*$ 满足 $\dot p_1=0$,解得 **平衡点**
|
||||
$$
|
||||
\dot{V}(x) = \frac{\partial V(x)}{\partial x} \cdot f(x, t)
|
||||
p_1^* = \frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}},
|
||||
\quad
|
||||
d^* \;=\;(N-1)\,p_1^*.
|
||||
$$
|
||||
**平衡时 $\dot{V}(x) = 0$**: 当且仅当系统处于平衡状态 $x = x_e$ 时,有 $\dot{V}(x) = 0$。
|
||||
**定义误差(偏离平衡的量)**
|
||||
$$
|
||||
e(t)=d(t)-d^*.
|
||||
$$
|
||||
其中
|
||||
$$
|
||||
d(t)=(N-1)\,p_1(t),
|
||||
\qquad
|
||||
d^*=(N-1)\,p_1^*.
|
||||
$$
|
||||
将 $d$ 和 $d^*$ 代入
|
||||
$$
|
||||
e(t)
|
||||
=d(t)-d^*
|
||||
=(N-1)\,p_1(t)\;-\;(N-1)\,p_1^*
|
||||
=(N-1)\,\bigl[p_1(t)-p_1^*\bigr].
|
||||
$$
|
||||
解得
|
||||
$$
|
||||
p_1(t)-p_1^* \;=\;\frac{e(t)}{\,N-1\,}
|
||||
\quad\Longrightarrow\quad
|
||||
p_1(t)
|
||||
=\frac{e(t)}{\,N-1\,}+p_1^*.
|
||||
$$
|
||||
**误差求导**
|
||||
$$
|
||||
\dot e(t) = \frac{d}{dt}\bigl[(N-1)(p_1-p_1^*)\bigr]
|
||||
= (N-1)\,\dot p_1(t),
|
||||
$$
|
||||
得到
|
||||
$$
|
||||
\dot e
|
||||
=(N-1)\Bigl[-(\lambda_{01}+\lambda_{10})\Bigl(\tfrac{e}{N-1}+p_1^*\Bigr)
|
||||
+\lambda_{01}\Bigr].\\\dot e = -(\lambda_{01}+\lambda_{10})\,e.
|
||||
$$
|
||||
这就是把原来以 $p_1$ 为自变量的微分方程,转写成以 "偏离平衡量" $e$ 为自变量的形式
|
||||
|
||||
同时在平衡附近的非平衡状态下,由于选定的李雅普诺夫函数“能量”不会增加,从而得到$\dot{V}(x) ≤ 0$
|
||||
记常数
|
||||
$$
|
||||
c = \lambda_{01}+\lambda_{10} >0,
|
||||
$$
|
||||
则误差模型就是一维线性常微分方程:
|
||||
$$
|
||||
\dot e = -\,c\,e.
|
||||
$$
|
||||
|
||||
#### 构造李雅普诺夫函数
|
||||
|
||||
对一维系统 $\dot e=-ce$($c>0$),自然选取
|
||||
$$
|
||||
V(e)=e^2
|
||||
$$
|
||||
作为李雅普诺夫函数,理由是:
|
||||
|
||||
- $V(e)>0$ 当且仅当 $e\neq0$;
|
||||
- 平衡点 $e=0$ 时,$V(0)=0$。
|
||||
|
||||
#### 计算 $V$ 的时间导数
|
||||
|
||||
对 $V$ 关于时间求导:
|
||||
$$
|
||||
\dot V(e)
|
||||
= \frac{d}{dt}\bigl(e^2\bigr)
|
||||
= 2\,e\,\dot e
|
||||
= 2\,e\,\bigl(-c\,e\bigr)
|
||||
= -2c\,e^2.
|
||||
$$
|
||||
|
||||
因为 $c>0$ 且 $e^2\ge0$,所以
|
||||
$$
|
||||
\boxed{\dot V(e)\;=\;-2c\,e^2\;\le\;0.}
|
||||
$$
|
||||
|
||||
- 当 $e\neq0$ 时,$\dot V<0$;
|
||||
- 当 $e=0$ 时,$\dot V=0$。
|
||||
|
||||
这正是“半负定”(negative semi-definite)的定义。
|
||||
|
||||
#### 结论
|
||||
|
||||
李雅普诺夫第二类定理告诉我们:
|
||||
|
||||
> 若存在一个函数 $V(e)$ 在平衡点处为 0、在邻域内正定,且其导数 $\dot V(e)$ 在该邻域内为半负定,则平衡点 $e=0$(即 $d=d^*$)是**稳定**的。
|
||||
|
||||
由于我们已经构造了满足上述条件的 $V(e)=e^2$,并验证了 $\dot V(e)\le0$,故平衡态 $d=d^*$ 是 **李雅普诺夫意义下稳定** 的。
|
||||
|
||||
|
||||
|
||||
## 网络特征谱参数的估算
|
||||
|
||||
### 基于奇异值分解改进幂迭代估算(集中式)
|
||||
|
||||
**输入**:矩阵 $B = A^T A$,目标特征值数量 $k$,收敛阈值 $\delta$
|
||||
**输出**:前 $k$ 个特征值 $\lambda_1' \geq \lambda_2' \geq \dots \geq \lambda_k'$ 及对应特征向量 $u_1', u_2', \dots, u_k'$
|
||||
|
||||
#### 1. 初始化
|
||||
|
||||
1. 随机生成初始非零向量 $v^{(0)}$,归一化:
|
||||
$$
|
||||
v^{(0)} \gets \frac{v^{(0)}}{\|v^{(0)}\|_2}
|
||||
$$
|
||||
|
||||
2. 设置已求得的特征值数量 $n \gets 0$,剩余矩阵 $B_{\text{res}} \gets B$
|
||||
|
||||
#### 2. 迭代求前k个特征值与特征向量
|
||||
|
||||
**While** $n < k$:
|
||||
|
||||
1. **幂迭代求当前最大特征值与特征向量**
|
||||
|
||||
- 初始化向量 $v^{(0)}$(若 $n=0$,用随机向量;否则用与已求特征向量正交的向量)
|
||||
|
||||
- **Repeat**:
|
||||
a. 计算 $v^{(t+1)} \gets B_{\text{res}} v^{(t)}$
|
||||
b. 归一化:
|
||||
$$
|
||||
v^{(t+1)}\gets \frac{v^{(t+1)}}{\|v^{(t+1)}\|_2}
|
||||
$$
|
||||
c. 计算 Rayleigh 商:
|
||||
$$
|
||||
y^{(t)} = \frac{(v^{(t)})^T B_{\text{res}} v^{(t)}}{(v^{(t)})^T v^{(t)}}
|
||||
$$
|
||||
|
||||
|
||||
d. **Until** $|y^{(t)} - y^{(t-1)}| < \delta$(收敛)
|
||||
|
||||
- 记录当前特征值与特征向量:
|
||||
$$
|
||||
\lambda_{n+1}' \gets y^{(t)}, \quad u_{n+1}' \gets v^{(t)}
|
||||
$$
|
||||
|
||||
2. **收缩矩阵以移除已求特征分量**
|
||||
每次收缩操作将已求得的特征值从矩阵中“移除”,使得剩余矩阵的谱(特征值集合)中次大特征值“升级”为最大特征值。
|
||||
|
||||
- 更新剩余矩阵:
|
||||
$$
|
||||
B_{\text{res}} \gets B_{\text{res}} - \lambda_{n+1}' u_{n+1}' (u_{n+1}')^T
|
||||
$$
|
||||
|
||||
- 确保 $B_{\text{res}}$ 的对称性(数值修正)
|
||||
|
||||
3. **增量计数**
|
||||
|
||||
- $n \gets n + 1$
|
||||
|
||||
|
||||
|
||||
### 主要符号表
|
||||
|
||||
| 符号 | 类型 | 含义 | 存储/计算位置 |
|
||||
| --------------- | -------- | ----------------------------------------------- | --------------- |
|
||||
| $n$ | 下标 | 当前计算的奇异值序号(从0开始) | 全局共识 |
|
||||
| $K$ | 常量 | 需要计算的前$K$大奇异值总数 | 预设参数 |
|
||||
| $j,k$ | 下标 | 节点编号($j$表示当前节点) | 本地存储 |
|
||||
| $𝒩_j$ | 集合 | 节点$j$的邻居节点集合 | 本地拓扑信息 |
|
||||
| $a_{jk}$ | 矩阵元素 | 邻接矩阵$A$中节点$j$与$k$的连接权值 | 节点$j$本地存储 |
|
||||
| $v_{n,j}^{(t)}$ | 向量分量 | 第$n$个右奇异向量在节点$j$的分量(第$t$次迭代) | 节点$j$存储 |
|
||||
| $u_{n,j}$ | 向量分量 | 第$n$个左奇异向量在节点$j$的分量 | 节点$j$计算存储 |
|
||||
| $\sigma_n$ | 标量 | 第$n$个奇异值 | 全局共识存储 |
|
||||
| $\delta$ | 标量 | 收敛阈值 | 预设参数 |
|
||||
|
||||
|
||||
|
||||
### 分布式幂迭代求前$K$大奇异对
|
||||
|
||||
**While** $n < K$:
|
||||
|
||||
1. **初始化**:
|
||||
|
||||
- 若 $n = 0$:
|
||||
|
||||
- 各节点$j$随机初始化 $v_{0,j}^{(0)} \sim \mathcal{N}(0,1)$
|
||||
|
||||
- 若 $n > 0$:
|
||||
|
||||
- **分布式Gram-Schmidt正交化**:
|
||||
$$
|
||||
v_{n,j}^{(0)} \gets v_{n,j}^{(0)} - \sum_{m=0}^{n-1} \underbrace{\text{Consensus}\left(\sum_k v_{m,k} v_{n,k}^{(0)}\right)}_{\text{全局内积}\langle v_m, v_n^{(0)} \rangle} v_{m,j}
|
||||
$$
|
||||
|
||||
- **分布式归一化**:
|
||||
$$
|
||||
v_{n,j}^{(0)} \gets \frac{v_{n,j}^{(0)}}{\sqrt{\text{Consensus}\left(\sum_k (v_{n,k}^{(0)})^2\right)}}
|
||||
$$
|
||||
|
||||
2. **迭代计算**:
|
||||
|
||||
- **Repeat**:
|
||||
a. **第一轮通信(计算$z=Av$)**:
|
||||
$$
|
||||
z_j^{(t)} = \sum_{k \in 𝒩_j} a_{jk} v_{n,k}^{(t)} \quad \text{(邻居交换$v_{n,k}^{(t)}$)}
|
||||
$$
|
||||
b. **第二轮通信(计算$y=A^T z$)**:
|
||||
$$
|
||||
y_j^{(t+1)} = \sum_{k \in 𝒩_j} a_{kj} z_k^{(t)} \quad \text{(邻居交换$z_k^{(t)}$)}
|
||||
$$
|
||||
c. **隐式收缩($n>0$时)**:
|
||||
$$
|
||||
y_j^{(t+1)} \gets y_j^{(t+1)} - \sum_{m=0}^{n-1} \sigma_m^2 v_{m,j} \cdot \underbrace{\text{Consensus}\left(\sum_k v_{m,k} y_k^{(t+1)}\right)}_{\text{投影系数计算}}
|
||||
$$
|
||||
d. **归一化**:
|
||||
$$
|
||||
v_{n,j}^{(t+1)} = \frac{y_j^{(t+1)}}{\sqrt{\text{Consensus}\left(\sum_k (y_k^{(t+1)})^2\right)}}
|
||||
$$
|
||||
e. **计算Rayleigh商**:
|
||||
$$
|
||||
\lambda^{(t)} = \text{Consensus}\left(\sum_k v_{n,k}^{(t)} y_k^{(t+1)}\right)
|
||||
$$
|
||||
f. **终止条件**:
|
||||
$$
|
||||
\text{If } \frac{|\lambda^{(t)} - \lambda^{(t-1)}|}{|\lambda^{(t)}|} < \delta \text{ then break}
|
||||
$$
|
||||
|
||||
3. **保存结果**:
|
||||
$$
|
||||
\sigma_n = \sqrt{\lambda^{(\text{final})}}, \quad v_{n,j} = v_{n,j}^{(\text{final})}
|
||||
$$
|
||||
|
||||
- 所有节点同步 $n \gets n + 1$
|
||||
|
||||
|
||||
|
||||
### 分布式计算左奇异向量$u_{n,j}$
|
||||
|
||||
对于邻接矩阵 $A \in \mathbb{R}^{N \times N}$,其奇异值分解为:
|
||||
$$
|
||||
A = U \Sigma V^T
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $U$ 的列向量 $\{u_n\}$ 是左奇异向量
|
||||
- $V$ 的列向量 $\{v_n\}$ 是右奇异向量
|
||||
- $\Sigma$ 是对角矩阵,元素 $\sigma_n$ 为奇异值
|
||||
|
||||
**左奇异向量的定义关系**:
|
||||
$$
|
||||
A v_n = \sigma_n u_n \quad \Rightarrow \quad u_n = \frac{1}{\sigma_n} A v_n
|
||||
$$
|
||||
展开为分量形式(对第 $j$ 个分量):
|
||||
$$
|
||||
u_{n,j} = \frac{1}{\sigma_n} \sum_{k=1}^N a_{jk} v_{n,k}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
**输入**:$\sigma_n$, $v_{n,j}$(来自幂迭代最终结果)
|
||||
|
||||
**For** $n = 0$ to $K-1$:
|
||||
|
||||
1. **本地计算**:
|
||||
$$
|
||||
u_{n,j} = \frac{1}{\sigma_n} \sum_{k \in 𝒩_j} a_{jk} v_{n,k} \quad \text{(需邻居节点发送$v_{n,k}$)}
|
||||
$$
|
||||
|
||||
2. **正交归一化**:
|
||||
|
||||
- **For** $m = 0$ to $n-1$:
|
||||
$$
|
||||
u_{n,j} \gets u_{n,j} - \text{Consensus}\left(\sum_k u_{m,k} u_{n,k}\right) \cdot u_{m,j}
|
||||
$$
|
||||
|
||||
- **归一化**:
|
||||
$$
|
||||
u_{n,j} \gets \frac{u_{n,j}}{\sqrt{\text{Consensus}\left(\sum_k u_{n,k}^2\right)}}
|
||||
$$
|
||||
|
||||
### 分布式重构邻接矩阵$A$
|
||||
|
||||
**输入**:$\sigma_n$, $u_{n,j}$, $v_{n,k}$
|
||||
|
||||
**For** 每个节点$j$并行执行:
|
||||
|
||||
1. **对每个邻居$k \in 𝒩_j$**:
|
||||
|
||||
- 请求节点$k$发送$v_{n,k}$($n=0,...,K-1$)
|
||||
|
||||
- 计算:
|
||||
$$
|
||||
a_{jk} = \sum_{n=0}^{K-1} \sigma_n u_{n,j} v_{n,k}
|
||||
$$
|
||||
|
||||
2. **非邻居元素**:
|
||||
$$
|
||||
a_{jk} = 0 \quad \text{for} \quad k \notin 𝒩_j
|
||||
$$
|
||||
|
||||
|
||||
|
||||
## 非稳态下动态特征参数的估算
|
||||
|
||||
### 一致性控制策略
|
||||
|
||||
1. **异步更新模型**
|
||||
|
||||
- 节点仅在离散时刻 $t_k^i$ 接收邻居信息,更新自身状态 $x_i(t)$。
|
||||
- 各节点的状态更新时刻是独立的
|
||||
|
||||
2. **延时处理**
|
||||
|
||||
- 若检测到延时,节点选择**最新收到的邻居状态**替代旧值(避免使用过期数据)。
|
||||
|
||||
3. **一致性协议设计**
|
||||
|
||||
- 无时延系统
|
||||
$$
|
||||
\dot{x}_i = \sum_{j \in N(t_k^i, i)} a_{ij}(t_k^i) \left( x_j(t_k^i) - x_i(t) \right)
|
||||
$$
|
||||
|
||||
| 参数 | 含义 |
|
||||
| --------------- | ------------------------------------------------------------ |
|
||||
| $\dot{x}_i$ | 节点 $i$ 的状态变化率(导数),表示 $x_i$ 随时间的变化速度。 |
|
||||
| $x_i(t)$ | 节点 $i$ 在时刻 $t$ 的**本地状态值**(如特征估计、传感器数据等)。 |
|
||||
| $x_j(t_k^i)$ | 节点 $i$ 在 $t_k^i$ 时刻收到的邻居节点 $j$ 的状态值。 |
|
||||
| $N(t_k^i, i)$ | 节点 $i$ 在 $t_k^i$ 时刻的**邻居集合**(可直接通信的节点)。 |
|
||||
| $a_{ij}(t_k^i)$ | **权重因子**,控制邻居 $j$ 对节点 $i$ 的影响权重,满足 $\sum_j a_{ij} = 1$。 |
|
||||
|
||||
- 有时延系统
|
||||
$$
|
||||
\dot{x}_i = \sum_{j \in N(t_k^i, i)} a_{ij}(t_k^i) \left( x_j(t_k^i - \tau_{ij}^k) - x_i(t) \right)
|
||||
$$
|
||||
|
||||
| 参数 | 含义 |
|
||||
| --------------------- | ------------------------------------------------------------ |
|
||||
| $\tau_{ij}^k$ | 节点 $j$ 到 $i$ 在时刻 $t_k^i$ 的**信息传输延时**。 |
|
||||
| $t_k^i - \tau_{ij}^k$ | 节点 $i$ 实际使用的邻居状态 $x_j$ 的**有效时刻**(扣除延时)。 |
|
||||
|
||||
- 权重$\alpha_{ij}$
|
||||
$$
|
||||
\text{有有效邻居时 } a_{ij}(t) = \begin{cases}
|
||||
\frac{\alpha_{ij}(t_k^i)}{\sum_{s \in N(t_k^i, i)} \alpha_{is}(t_k^i)}, & \text{若 } j \in N(t_k^i, i) \\
|
||||
0, & \text{若 } j \notin N(t_k^i, i)
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$$
|
||||
\text{无有效邻居时 } a_{ij}(t) = \begin{cases}
|
||||
1, & \text{若 } j = i \\
|
||||
0, & \text{若 } j \neq i
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
4. **通信拓扑定义**
|
||||
|
||||
- 引入 **$G^0(t)$**:实际成功通信的瞬时拓扑(非理想链路 $G(t)$),强调**有效信息传递**而非物理连通性。
|
||||
|
||||
|
||||
|
||||
### 收敛性分析
|
||||
|
||||
动态网络的收敛条件:
|
||||
|
||||
- 在节点移动导致的**异步通信**和**随机延时**下,只要网络拓扑满足**有限时间内的联合连通性**(即时间窗口内信息能传递到全网),所有节点的状态 *$x_i$* 最终会收敛到同一全局值。 (平均代数连通度 > 0 == 动态网络拓扑的平均拉普拉斯矩阵的第二小特征值>0 )
|
||||
|
||||
- **无需时刻连通**:允许瞬时断连,但长期需保证信息能通过动态链路传递。
|
||||
|
||||
|
||||
|
||||
### 基于 UKF 的滤波估算
|
||||
|
||||
| | KF | EKF | UKF |
|
||||
| -------------- | -------- | ---------- | ---------- |
|
||||
| **线性要求** | 严格线性 | 弱非线性 | 强非线性 |
|
||||
| **可微要求** | - | 必须可微 | 不要求 |
|
||||
| **计算复杂度** | 低 | 中 | 中 |
|
||||
| **适用场景** | 线性系统 | 平滑非线性 | 剧烈非线性 |
|
||||
|
||||
**本文基于UKF:**
|
||||
|
||||
- 采用**确定性采样(Sigma点)**直接近似非线性分布
|
||||
- 完全规避对 *f*(*x*) 和 *h*(*x*) 的求导需求
|
||||
- 保持高斯系统假设
|
||||
- 允许函数不连续/不可微
|
||||
- 适应拓扑突变等非线性情况
|
||||
|
||||
|
||||
|
||||
### UKF 具体步骤
|
||||
|
||||
#### **符号说明**
|
||||
|
||||
- **$i$**: 节点索引,$N$ 为总节点数
|
||||
- **$x_i(k)$**: 节点 $i$ 在时刻 $k$ 的状态分量 (特征向量$x$)
|
||||
- **$b_i(k)$**: 节点 $i$ 的本地状态估计值 ($A^TAx$)
|
||||
- **$a_{ij}$**: 邻接矩阵元素(链路权重)
|
||||
- **$Q_k, R_k$**: 过程噪声与观测噪声协方差
|
||||
- **$\mathcal{X}_{i,j}$**: 节点 $i$ 的第 $j$ 个 Sigma 点
|
||||
- **$W_j^{(m)}, W_j^{(c)}$**: Sigma 点权重(均值和协方差)
|
||||
|
||||
#### **Step 1: 分布式初始化**
|
||||
|
||||
1. **节点状态初始化**:
|
||||
- 每个节点 $i$ 随机生成初始状态分量 $x_i(0)$。
|
||||
- 本地状态估计 $b_i(0)$ 初始化为 $x_i(0)$。
|
||||
|
||||
---
|
||||
|
||||
#### **Step 2: 生成 Sigma 点(确定性采样)**
|
||||
|
||||
**在每个节点本地执行**:
|
||||
|
||||
1. **计算 Sigma 点**:
|
||||
$$
|
||||
\begin{aligned}
|
||||
\mathcal{X}_{i,0} &= \hat{b}_{i,k-1} \\
|
||||
\mathcal{X}_{i,j} &= \hat{b}_{i,k-1} + \left( \sqrt{(n+\lambda) P_{i,k-1}} \right)_j \quad (j=1,\dots,n) \\
|
||||
\mathcal{X}_{i,j+n} &= \hat{b}_{i,k-1} - \left( \sqrt{(n+\lambda) P_{i,k-1}} \right)_j \quad (j=1,\dots,n)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
- **$\lambda = \alpha^2 (n + \kappa) - n$**(缩放因子,$\alpha$ 控制分布范围,$\kappa$ 通常取 0)
|
||||
- **$\sqrt{(n+\lambda) P}$** 为协方差矩阵的平方根(如 Cholesky 分解)
|
||||
|
||||
2. **计算 Sigma 点权重**:
|
||||
$$
|
||||
\begin{aligned}
|
||||
W_0^{(m)} &= \frac{\lambda}{n + \lambda} \quad &\text{(中心点均值权重)} \\
|
||||
W_0^{(c)} &= \frac{\lambda}{n + \lambda} + (1 - \alpha^2 + \beta) \quad &\text{(中心点协方差权重)} \\
|
||||
W_j^{(m)} = W_j^{(c)} &= \frac{1}{2(n + \lambda)} \quad (j=1,\dots,2n) \quad &\text{(对称点权重)}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
- **$\beta$** 为高阶矩调节参数(高斯分布时取 2 最优)
|
||||
|
||||
---
|
||||
|
||||
#### **Step 3: 预测步骤(时间更新)**
|
||||
|
||||
1. **传播 Sigma 点**:
|
||||
$$
|
||||
\mathcal{X}_{i,j,k|k-1}^* = f(\mathcal{X}_{i,j,k-1}) + q_k \quad (j=0,\dots,2n)
|
||||
$$
|
||||
|
||||
- **$f(\cdot)$** 为非线性状态转移函数
|
||||
- **$q_k$** 为过程噪声 ,反映网络拓扑动态变化(如节点移动导致的链路扰动)。
|
||||
|
||||
2. **计算预测均值和协方差**:
|
||||
$$
|
||||
\hat{b}_{i,k|k-1} = \sum_{j=0}^{2n} W_j^{(m)} \mathcal{X}_{i,j,k|k-1}^*
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{i,k|k-1} = \sum_{j=0}^{2n} W_j^{(c)} \left( \mathcal{X}_{i,j,k|k-1}^* - \hat{b}_{i,k|k-1} \right) \left( \mathcal{X}_{i,j,k|k-1}^* - \hat{b}_{i,k|k-1} \right)^T + Q_k
|
||||
$$
|
||||
|
||||
- **$Q_k$** 为过程噪声协方差
|
||||
|
||||
---
|
||||
|
||||
#### **Step 4: 分布式观测生成**
|
||||
|
||||
1. **邻居状态融合**:
|
||||
|
||||
- 节点 $i$ 从邻居 $j$ 获取状态 $x_j(k)$,生成观测值:
|
||||
$$
|
||||
b_i^H(k) = \sum_{j=1}^N a_{ji} b_{0,j}(k) + r_k, \quad b_{0,j}(k) = \sum_{j=1}^N a_{ij} x_j(k)
|
||||
$$
|
||||
|
||||
- **$r_k$** 为观测噪声 ,来自分布式通信中的信息传输误差(如延时、丢包)
|
||||
|
||||
---
|
||||
|
||||
#### **Step 5: 观测更新(测量更新)**
|
||||
|
||||
1. **观测 Sigma 点**:
|
||||
$$
|
||||
\mathcal{Z}_{i,j,k|k-1} = h(\mathcal{X}_{i,j,k|k-1}^*) + r_k \quad (j=0,\dots,2n)
|
||||
$$
|
||||
|
||||
- **$h(\cdot)$** 为非线性观测函数
|
||||
|
||||
2. **计算观测统计量**:
|
||||
$$
|
||||
\hat{z}_{i,k|k-1} = \sum_{j=0}^{2n} W_j^{(m)} \mathcal{Z}_{i,j,k|k-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{i,zz} = \sum_{j=0}^{2n} W_j^{(c)} \left( \mathcal{Z}_{i,j,k|k-1} - \hat{z}_{i,k|k-1} \right) \left( \mathcal{Z}_{i,j,k|k-1} - \hat{z}_{i,k|k-1} \right)^T + R_k
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{i,xz} = \sum_{j=0}^{2n} W_j^{(c)} \left( \mathcal{X}_{i,j,k|k-1}^* - \hat{b}_{i,k|k-1} \right) \left( \mathcal{Z}_{i,j,k|k-1} - \hat{z}_{i,k|k-1} \right)^T
|
||||
$$
|
||||
|
||||
- **$R_k$** 为观测噪声协方差
|
||||
|
||||
3. **计算卡尔曼增益并更新状态**:
|
||||
$$
|
||||
K_{i,k} = P_{i,xz} P_{i,zz}^{-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\hat{b}_{i,k|k} = \hat{b}_{i,k|k-1} + K_{i,k} \left( b_i^H(k) - \hat{z}_{i,k|k-1} \right)
|
||||
$$
|
||||
|
||||
$$
|
||||
P_{i,k|k} = P_{i,k|k-1} - K_{i,k} P_{i,zz} K_{i,k}^T
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
#### **Step 6: 全局一致性计算**
|
||||
|
||||
1. **瑞利商计算**:
|
||||
|
||||
- 所有节点通过一致性协议交换 $\hat{b}_{i,k|k}$,计算全局状态:
|
||||
$$
|
||||
y(k) = \frac{\sum_{i=1}^N x_i(k) \hat{b}_{i,k|k}}{\sum_{i=1}^N x_i^2(k)}
|
||||
$$
|
||||
|
||||
2. **正交化**:
|
||||
|
||||
- 更新本地状态分量:
|
||||
$$
|
||||
x_i(k+1) = \frac{\hat{b}_{i,k|k}}{\|\hat{b}(k)\|_2}
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
#### **Step 7: 收敛判断**
|
||||
|
||||
- 若 $y(k)$ 收敛,输出 $\sigma = \sqrt{y(k)}$;否则返回 **Step 2**。
|
||||
|
||||
|
||||
|
||||
## 稳态下动态特征参数的估算
|
||||
|
||||
稳态下,网络拓扑变化趋于平稳,奇异值的**理论曲线不再随时间变化**(实际值因噪声围绕理论值波动)。此时采用**集中式多观测值卡尔曼滤波**
|
||||
|
||||
### 多观测值滤波算法
|
||||
|
||||
- **核心思想**:利用相邻奇异值的**有序性约束**($\sigma_{n-1} \leq \sigma_n \leq \sigma_{n+1}$),构造双观测值作为上下界,限制估计范围。
|
||||
|
||||
- **观测值生成**:
|
||||
对第$n$大奇异值$\sigma_n$,其观测值$y_n$由相邻奇异值线性组合:
|
||||
$$
|
||||
y_n = C_1 \sigma_{n-1} + C_2 \sigma_{n+1}
|
||||
$$
|
||||
|
||||
- **系数$C_1, C_2$**:根据$\sigma_{n-1}$和$\sigma_{n+1}$的权重动态调整(如距离比例)。
|
||||
- **物理意义**:将$\sigma_{n-1}$和$\sigma_{n+1}$作为$\sigma_n$的**下界和上界**,避免单观测值因噪声导致的估计偏离。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
疑问:
|
||||
|
||||
第三章的目的是什么?先分解再重构的意义在?
|
||||
|
||||
状态转移函数和观测函数怎么来?UKF每次预测单奇异值,如何同时预测K个呢?
|
||||
|
||||
|
||||
|
||||
卡尔曼滤波 观测值怎么来?是否需要拟合历史数据生成观测值?还是根据第三章分布式幂迭代求真实的特征值?
|
||||
|
||||
458
自学/Redis.md
458
自学/Redis.md
@ -1,34 +1,116 @@
|
||||
# Redis
|
||||
|
||||
## Redis基本定义
|
||||
|
||||
Redis是一个基于**内存**的key-value结构数据库。Redis 是互联网技术领域使用最为广泛的**存储中间件**。
|
||||
|
||||
Redis是用C语言开发的一个开源的高性能键值对(key-value)数据库,官方提供的数据是可以达到100000+的QPS(每秒内查询次数)。它存储的value类型比较丰富,也被称为结构化的**NoSql数据库**(非关系型)。
|
||||
Redis是用C语言开发的一个开源的**高性能键值对(key-value)数据库**,官方提供的数据是可以达到100000+的QPS(每秒内查询次数)。它存储的value类型比较丰富,也被称为结构化的**NoSql数据库**(非关系型)。
|
||||
|
||||
**主要特点:**
|
||||
**典型场景**:
|
||||
|
||||
- 基于内存存储,读写性能高
|
||||
- 适合存储热点数据(热点商品、资讯、新闻)
|
||||
- 企业应用广泛
|
||||
- 热点数据缓存(商品/资讯/秒杀)
|
||||
- 会话管理(Session)
|
||||
- 排行榜/计数器
|
||||
- 消息队列(Stream)
|
||||
|
||||
**服务启动/停止:**
|
||||
**NoSQL数据库**:
|
||||
|
||||
- 键值型(Redis)
|
||||
|
||||
- 文档型(MongoDB)
|
||||
- 列存储(HBase)
|
||||
- 图数据库(Neo4j)
|
||||
|
||||
|
||||
|
||||
## 下载与使用
|
||||
|
||||
Redis安装包分为windows版和Linux版:
|
||||
|
||||
- Windows版下载地址:https://github.com/microsoftarchive/redis/releases
|
||||
- Linux版下载地址: https://download.redis.io/releases/
|
||||
|
||||
| **角色** | **作用** | **典型示例** |
|
||||
| :--------------: | :----------------------------------------------------------: | :----------------------------------: |
|
||||
| **Redis 服务端** | 数据存储的核心,负责接收/执行命令、管理内存、持久化数据等。需先启动服务端才能使用。 | `redis-server`(默认监听 6379 端口) |
|
||||
| **Redis 客户端** | 连接服务端并发送命令(如 `GET/SET`),获取返回结果。可以是命令行工具或代码库。 | `redis-cli`、Java 的 Jedis 库 |
|
||||
|
||||
|
||||
|
||||
**windows下服务启动/停止:**
|
||||
|
||||
启动:
|
||||
|
||||
```bash
|
||||
redis-server.exe redis.windows.conf
|
||||
```
|
||||
|
||||
|
||||
|
||||
这种方式关闭命令行后Redis服务又停止了!
|
||||
|
||||
解决方法:**安装为 Windows 服务**
|
||||
|
||||
```
|
||||
redis-server --service-install redis.windows.conf --service-name Redis
|
||||
redis-server --service-start
|
||||
```
|
||||
|
||||
停止:
|
||||
|
||||
```bash
|
||||
ctrl+c
|
||||
```
|
||||
|
||||
|
||||
|
||||
**客户端连接:**
|
||||
|
||||
redis-cli.exe (本地)
|
||||
直接运行 `redis-cli.exe` 时,它会尝试连接 **本机(127.0.0.1)的 Redis 服务端**,并使用默认端口 **6379**。
|
||||
等价于手动指定参数:
|
||||
|
||||
```bash
|
||||
redis-cli -h 127.0.0.1 -p 6379
|
||||
```
|
||||
|
||||
指定连接:
|
||||
|
||||
```bash
|
||||
redis-cli -h <IP> -p <端口> -a <密码>
|
||||
redis-cli -h 192.168.1.100 -p 6379 -a yourpassword
|
||||
```
|
||||
|
||||
退出连接:exit
|
||||
|
||||
|
||||
|
||||
**修改Redis配置文件**
|
||||
|
||||
设置Redis服务密码,修改redis.windows.conf(windows) redis.conf(linux)
|
||||
|
||||
```bash
|
||||
requirepass 123456
|
||||
```
|
||||
|
||||
修改redis服务端口
|
||||
|
||||
```bash
|
||||
port 6379
|
||||
```
|
||||
|
||||
|
||||
|
||||
**Redis客户端图形工具**
|
||||
|
||||
默认提供的客户端连接工具界面不太友好,可以使用Another Redis Desktop Manager.exe ,类似Navicat连mysql。
|
||||
|
||||
redis-cli.exe -h localhost -p 6379 -a 123456 (指定连接)
|
||||
|
||||
exit
|
||||
|
||||
## Redis数据类型
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7ckos-2.png" alt="image-20221130190150749" style="zoom:50%;" />
|
||||
|
||||
**解释说明:**
|
||||
Redis存储的是key-value结构的数据,其中key是字符串类型,value有5种常用的数据类型:
|
||||
|
||||
- 字符串(string):普通字符串,Redis中最简单的数据类型
|
||||
- 哈希(hash):也叫散列,类似于Java中的HashMap结构。(套娃)
|
||||
@ -40,6 +122,35 @@ exit
|
||||
|
||||
## Redis常用命令
|
||||
|
||||
### 通用命令
|
||||
|
||||
Redis的通用命令是不分数据类型的,都可以使用的命令:
|
||||
|
||||
- KEYS pattern **查找**所有符合给定模式( pattern)的 key
|
||||
|
||||
- **`pattern`**:匹配模式,支持通配符:
|
||||
|
||||
- `*`:匹配任意多个字符(包括空字符)
|
||||
- `?`:匹配单个字符
|
||||
- `[abc]`:匹配 `a`、`b` 或 `c` 中的任意一个字符
|
||||
- `[a-z]`:匹配 `a` 到 `z` 之间的任意一个字符
|
||||
|
||||
- ```bash
|
||||
KEYS user:* #可以返回 形如 "user:1" "user:2" 的 key
|
||||
```
|
||||
|
||||
- ```bash
|
||||
KEYS * #查找所有key
|
||||
```
|
||||
|
||||
- EXISTS key 检查给定 key 是否存在
|
||||
|
||||
- TYPE key 返回 key 所储存的值的类型
|
||||
|
||||
- DEL key 该命令用于在 key 存在是删除 key
|
||||
|
||||
|
||||
|
||||
### 字符串
|
||||
|
||||
Redis 中字符串类型常用命令:
|
||||
@ -47,7 +158,9 @@ Redis 中字符串类型常用命令:
|
||||
- **SET** key value 设置指定key的值
|
||||
- **GET** key 获取指定key的值
|
||||
- **SETEX** key seconds value 设置指定key的值,并将 key 的过期时间设为 seconds 秒(验证码)
|
||||
- **SETNX** key value 只有在 key 不存在时设置 key 的值
|
||||
- **SETNX** key value 只有在 key不存在时设置 key 的值
|
||||
|
||||
|
||||
|
||||
### 哈希操作
|
||||
|
||||
@ -61,31 +174,59 @@ Redis hash 是一个string类型的 field 和 value 的映射表,hash特别适
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7cyeg-2.png" alt="image-20221130193121969" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
### 列表操作
|
||||
|
||||
Redis 列表是简单的字符串列表,按照插入顺序排序,常用命令:
|
||||
Redis 列表是简单的**字符串列表**,按照插入顺序排序,常用命令:
|
||||
|
||||
- **LPUSH** key value1 将一个值插入到列表头部
|
||||
|
||||
- **RPUSH** key value1 [value2] 将一个或多个值插入到列表尾部
|
||||
|
||||
- ```bash
|
||||
RPUSH mylist "world" "redis" "rpush" #多个值插入
|
||||
```
|
||||
|
||||
- **LRANGE** key start stop 获取列表指定范围内的元素(这里L代表List 不是Left)
|
||||
|
||||
- ```bash
|
||||
LRANGE mylist 0 -1 #获取整个列表
|
||||
```
|
||||
|
||||
- **LPUSH** key value1 [value2] 将一个或多个值插入到列表头部
|
||||
- **LRANGE** key start stop 获取列表指定范围内的元素
|
||||
- **RPOP** key 移除并获取列表最后一个元素
|
||||
- **LLEN** key 获取列表长度
|
||||
|
||||
- **RPOP** key 移除并获取列表最后一个元素
|
||||
|
||||
- **BRPOP** key1 [key2 ] timeout 移出并获取列表的最后一个元素, 如果列表没有元素会阻塞列表直到等待超 时或发现可弹出元素为止
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7cqgp-2.png" alt="image-20221130193332666" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
### 集合操作
|
||||
|
||||
Redis set 是string类型的无序集合。集合成员是唯一的,这就意味着集合中不能出现重复的数据,常用命令:
|
||||
Redis set 是**string类型的无序集合**。集合成员是唯一的,这就意味着集合中不能出现重复的数据,常用命令:
|
||||
|
||||
- **SADD** key member1 [member2] 向集合添加一个或多个成员
|
||||
|
||||
```bash
|
||||
# 添加单个成员
|
||||
SADD fruits "apple"
|
||||
|
||||
# 添加多个成员(自动去重)
|
||||
SADD fruits "banana" "orange" "apple" # "apple" 已存在,不会重复添加
|
||||
```
|
||||
- **SMEMBERS** key 返回集合中的所有成员
|
||||
- **SCARD** key 获取集合的成员数
|
||||
- **SCARD** key 获取集合的成员数(基数**Cardinality**)
|
||||
- **SINTER** key1 [key2] 返回给定所有集合的交集
|
||||
- **SUNION** key1 [key2] 返回所有给定集合的并集
|
||||
- **SREM** key member1 [member2] 移除集合中一个或多个成员
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7d7ff-2.png" alt="image-20221130193532735" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
### 有序集合
|
||||
|
||||
Redis有序集合是string类型元素的集合,且不允许有重复成员。每个元素都会关联一个double类型的分数。常用命令:
|
||||
@ -99,11 +240,282 @@ Redis有序集合是string类型元素的集合,且不允许有重复成员。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7c9il-2.png" alt="image-20221130193951036" style="zoom:67%;" />
|
||||
|
||||
### 通用命令
|
||||
|
||||
Redis的通用命令是不分数据类型的,都可以使用的命令:
|
||||
|
||||
- KEYS pattern 查找所有符合给定模式( pattern)的 key
|
||||
- EXISTS key 检查给定 key 是否存在
|
||||
- TYPE key 返回 key 所储存的值的类型
|
||||
- DEL key 该命令用于在 key 存在是删除 key
|
||||
## Java中操作Redis
|
||||
|
||||
Spring Data Redis 是 Spring 的一部分,提供了在 Spring 应用中通过简单的配置就可以访问 Redis 服务,就如同我们使用JDBC操作MySQL数据库一样。
|
||||
|
||||
网址:https://spring.io/projects/spring-data-redis
|
||||
|
||||
### 环境搭建
|
||||
|
||||
进入到sky-server模块
|
||||
|
||||
**1). 导入Spring Data Redis的maven坐标(已完成)**
|
||||
|
||||
```java
|
||||
<dependency>
|
||||
<groupId>org.springframework.boot</groupId>
|
||||
<artifactId>spring-boot-starter-data-redis</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
**2). 配置Redis数据源**
|
||||
|
||||
在application-dev.yml中添加
|
||||
|
||||
```java
|
||||
sky:
|
||||
redis:
|
||||
host: localhost
|
||||
port: 6379
|
||||
password: 123456
|
||||
database: 10
|
||||
```
|
||||
|
||||
**解释说明:**
|
||||
|
||||
database:指定使用Redis的哪个数据库,Redis服务启动后默认有16个数据库,编号分别是从0到15。
|
||||
|
||||
可以通过修改Redis配置文件来指定数据库的数量。
|
||||
|
||||
在application.yml中添加读取application-dev.yml中的相关Redis配置
|
||||
|
||||
```java
|
||||
spring:
|
||||
profiles:
|
||||
active: dev
|
||||
redis:
|
||||
host: ${sky.redis.host}
|
||||
port: ${sky.redis.port}
|
||||
password: ${sky.redis.password}
|
||||
database: ${sky.redis.database}
|
||||
```
|
||||
|
||||
**3). 编写配置类,创建RedisTemplate对象**
|
||||
|
||||
```java
|
||||
@Configuration
|
||||
@Slf4j
|
||||
public class RedisConfiguration {
|
||||
@Bean
|
||||
public RedisTemplate redisTemplate(RedisConnectionFactory redisConnectionFactory){
|
||||
log.info("开始创建redis模板对象...");
|
||||
RedisTemplate redisTemplate = new RedisTemplate();
|
||||
//设置redis的连接工厂对象
|
||||
redisTemplate.setConnectionFactory(redisConnectionFactory);
|
||||
//设置redis key的序列化器
|
||||
redisTemplate.setKeySerializer(new StringRedisSerializer());
|
||||
return redisTemplate;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**解释说明:**
|
||||
|
||||
当前配置类不是必须的,因为 Spring Boot 框架会自动装配 RedisTemplate 对象,但是默认的key序列化器为
|
||||
|
||||
`JdkSerializationRedisSerializer`,存到 Redis 里会是二进制格式,这里把 key 的序列化器指定为 `StringRedisSerializer`,就会把所有的 key 都以 UTF‑8 字符串形式写入 Redis,方便观测和调试
|
||||
|
||||
|
||||
|
||||
### 功能测试
|
||||
|
||||
**通过RedisTemplate对象操作Redis**,注意要Another Redis Desktop中刷新一下数据库,才能看到数据。
|
||||
|
||||
**字符串测试**
|
||||
|
||||
```java
|
||||
@DataRedisTest
|
||||
@Import(com.sky.config.RedisConfiguration.class)
|
||||
public class SpringDataRedisTest {
|
||||
@Autowired
|
||||
private RedisTemplate redisTemplate;
|
||||
@Test
|
||||
public void testRedisTemplate(){
|
||||
System.out.println(redisTemplate);
|
||||
}
|
||||
@Test
|
||||
public void testString(){
|
||||
// SET city "北京"
|
||||
redisTemplate.opsForValue().set("city", "北京");
|
||||
|
||||
// GET city
|
||||
String city = (String) redisTemplate.opsForValue().get("city");
|
||||
System.out.println(city);
|
||||
|
||||
// SETEX code 180 "1234" (3 分钟 = 180 秒)
|
||||
redisTemplate.opsForValue().set("code", "1234", 3, TimeUnit.MINUTES);
|
||||
|
||||
// SETNX lock "1"
|
||||
redisTemplate.opsForValue().setIfAbsent("lock", "1");
|
||||
|
||||
// (由于上一步 lock 已存在,这里相当于不执行)
|
||||
// SETNX lock "2"
|
||||
redisTemplate.opsForValue().setIfAbsent("lock", "2");
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**哈希测试**
|
||||
|
||||
```java
|
||||
@Test
|
||||
public void testHash(){
|
||||
HashOperations hashOperations = redisTemplate.opsForHash();
|
||||
|
||||
// HSET 100 "name" "tom"
|
||||
hashOperations.put("100", "name", "tom");
|
||||
|
||||
// HSET 100 "age" "20"
|
||||
hashOperations.put("100", "age", "20");
|
||||
|
||||
// HGET 100 "name"
|
||||
String name = (String) hashOperations.get("100", "name");
|
||||
System.out.println(name);
|
||||
|
||||
// HKEYS 100
|
||||
Set keys = hashOperations.keys("100");
|
||||
System.out.println(keys);
|
||||
|
||||
// HVALS 100
|
||||
List values = hashOperations.values("100");
|
||||
System.out.println(values);
|
||||
|
||||
// HDEL 100 "age"
|
||||
hashOperations.delete("100", "age");
|
||||
}
|
||||
```
|
||||
|
||||
get获得的是Object类型,keys获得的是set类型,values获得的是List
|
||||
|
||||
|
||||
|
||||
**3). 操作列表类型数据**
|
||||
|
||||
```java
|
||||
@Test
|
||||
public void testList(){
|
||||
ListOperations listOperations = redisTemplate.opsForList();
|
||||
|
||||
// LPUSH mylist "a" "b" "c"
|
||||
listOperations.leftPushAll("mylist", "a", "b", "c");
|
||||
|
||||
// LPUSH mylist "d"
|
||||
listOperations.leftPush("mylist", "d");
|
||||
|
||||
// LRANGE mylist 0 -1
|
||||
List mylist = listOperations.range("mylist", 0, -1);
|
||||
System.out.println(mylist);
|
||||
|
||||
// RPOP mylist
|
||||
listOperations.rightPop("mylist");
|
||||
|
||||
// LLEN mylist
|
||||
Long size = listOperations.size("mylist");
|
||||
System.out.println(size);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**4). 操作集合类型数据**
|
||||
|
||||
```java
|
||||
@Test
|
||||
public void testSet(){
|
||||
SetOperations setOperations = redisTemplate.opsForSet();
|
||||
|
||||
// SADD set1 "a" "b" "c" "d"
|
||||
setOperations.add("set1", "a", "b", "c", "d");
|
||||
|
||||
// SADD set2 "a" "b" "x" "y"
|
||||
setOperations.add("set2", "a", "b", "x", "y");
|
||||
|
||||
// SMEMBERS set1
|
||||
Set members = setOperations.members("set1");
|
||||
System.out.println(members);
|
||||
|
||||
// SCARD set1
|
||||
Long size = setOperations.size("set1");
|
||||
System.out.println(size);
|
||||
|
||||
// SINTER set1 set2
|
||||
Set intersect = setOperations.intersect("set1", "set2");
|
||||
System.out.println(intersect);
|
||||
|
||||
// SUNION set1 set2
|
||||
Set union = setOperations.union("set1", "set2");
|
||||
System.out.println(union);
|
||||
|
||||
// SREM set1 "a" "b"
|
||||
setOperations.remove("set1", "a", "b");
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**5). 操作有序集合类型数据**
|
||||
|
||||
```java
|
||||
@Test
|
||||
public void testZset(){
|
||||
ZSetOperations zSetOperations = redisTemplate.opsForZSet();
|
||||
|
||||
// ZADD zset1 10 "a"
|
||||
zSetOperations.add("zset1", "a", 10);
|
||||
|
||||
// ZADD zset1 12 "b"
|
||||
zSetOperations.add("zset1", "b", 12);
|
||||
|
||||
// ZADD zset1 9 "c"
|
||||
zSetOperations.add("zset1", "c", 9);
|
||||
|
||||
// ZRANGE zset1 0 -1
|
||||
Set zset1 = zSetOperations.range("zset1", 0, -1);
|
||||
System.out.println(zset1);
|
||||
|
||||
// ZINCRBY zset1 10 "c"
|
||||
zSetOperations.incrementScore("zset1", "c", 10);
|
||||
|
||||
// ZREM zset1 "a" "b"
|
||||
zSetOperations.remove("zset1", "a", "b");
|
||||
}
|
||||
```
|
||||
|
||||
**6). 通用命令操作**
|
||||
|
||||
- `*` 匹配零个或多个字符。
|
||||
- `?` 匹配任何单个字符。
|
||||
- `[abc]` 匹配方括号内的任一字符(本例中为 'a'、'b' 或 'c')。
|
||||
- `[^abc]` 或 `[!abc]` 匹配任何不在方括号中的单个字符。
|
||||
|
||||
```java
|
||||
@Test
|
||||
public void testCommon(){
|
||||
// KEYS *
|
||||
Set keys = redisTemplate.keys("*");
|
||||
System.out.println(keys);
|
||||
|
||||
// EXISTS name
|
||||
Boolean existsName = redisTemplate.hasKey("name");
|
||||
System.out.println("name exists? " + existsName);
|
||||
|
||||
// EXISTS set1
|
||||
Boolean existsSet1 = redisTemplate.hasKey("set1");
|
||||
System.out.println("set1 exists? " + existsSet1);
|
||||
|
||||
for (Object key : keys) {
|
||||
// TYPE <key>
|
||||
DataType type = redisTemplate.type(key);
|
||||
System.out.println(key + " -> " + type.name());
|
||||
}
|
||||
|
||||
// DEL mylist
|
||||
redisTemplate.delete("mylist");
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -108,7 +108,7 @@ String sortedStr = new String(charArray);
|
||||
|
||||
- `charAt(int index)` 方法返回指定索引处的 `char` 值。
|
||||
- `char` 是基本数据类型,占用 2 个字节,表示一个 Unicode 字符。
|
||||
- HashSet<Character> set = new HashSet<Character>();
|
||||
- `HashSet<Character> set = new HashSet<Character>();`
|
||||
|
||||
取子串:
|
||||
|
||||
|
||||
410
自学/微信小程序.md
Normal file
410
自学/微信小程序.md
Normal file
@ -0,0 +1,410 @@
|
||||
# 微信小程序
|
||||
|
||||
转载自黑马程序员。
|
||||
|
||||
## 微信小程序开发
|
||||
|
||||
### 介绍
|
||||
|
||||
小程序是一种新的开放能力,开发者可以快速地开发一个小程序。可以在微信内被便捷地获取和传播,同时具有出色的使用体验。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3lwd-0.png" alt="image-20221203204712437" style="zoom:50%;" />
|
||||
|
||||
**官方网址:**https://mp.weixin.qq.com/cgi-bin/wx?token=&lang=zh_CN
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3tif-0.png" alt="image-20221203205305487" style="zoom:50%;" />
|
||||
|
||||
小程序主要运行微信内部,可通过上述网站来整体了解微信小程序的开发。
|
||||
|
||||
**首先,**在进行小程序开发时,需要先去注册一个小程序,在注册的时候,它实际上又分成了不同的注册的主体。我们可以以个人的身份来注册一个小程序,当然,也可以以企业政府、媒体或者其他组织的方式来注册小程序。那么,不同的主体注册小程序,最终开放的权限也是不一样的。比如以个人身份来注册小程序,是无法开通支付权限的。若要提供支付功能,必须是企业、政府或者其它组织等。所以,不同的主体注册小程序后,可开发的功能是不一样的。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4ecz-0.png" alt="image-20221203210640473" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**然后,**微信小程序我们提供的一些开发的支持,实际上微信的官方是提供了一系列的工具来帮助开发者快速的接入
|
||||
并且完成小程序的开发,提供了完善的开发文档,并且专门提供了一个开发者工具,还提供了相应的设计指南,同时也提供了一些小程序体验DEMO,可以快速的体验小程序实现的功能。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4dy6-0.png" alt="image-20221203211226920" style="zoom:50%;" />
|
||||
|
||||
**最后,**开发完一个小程序要上线,也给我们提供了详细地接入流程。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg47yt-0.png" alt="image-20221203211535565" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
### 准备工作
|
||||
|
||||
开发微信小程序之前需要做如下准备工作:
|
||||
|
||||
- 注册小程序
|
||||
- 完善小程序信息
|
||||
- 下载开发者工具
|
||||
|
||||
**1). 注册小程序**
|
||||
|
||||
注册地址:https://mp.weixin.qq.com/wxopen/waregister?action=step1
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3qwt-0.png" alt="image-20221203212348111" style="zoom: 50%;" />
|
||||
|
||||
|
||||
|
||||
**2). 完善小程序信息**
|
||||
|
||||
登录小程序后台:https://mp.weixin.qq.com/
|
||||
|
||||
两种登录方式选其一即可
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg49qm-0.png" alt="image-20221203212454040" style="zoom:50%;" /> <img src="https://pic.bitday.top/i/2025/04/22/sktai8-0.png" alt="image-20221203212508081" style="zoom:50%;" />
|
||||
|
||||
完善小程序信息、小程序类目
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4bya-0.png" alt="image-20221203212615981" style="zoom:50%;" />
|
||||
|
||||
查看小程序的 AppID与AppSecret
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4xtx-0.png" alt="image-20221203212702993" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**3). 下载开发者工具**
|
||||
|
||||
资料中已提供,无需下载,熟悉下载步骤即可。
|
||||
|
||||
下载地址: https://developers.weixin.qq.com/miniprogram/dev/devtools/stable.html
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4tyl-0.png" alt="image-20221203212836364" style="zoom:50%;" />
|
||||
|
||||
扫描登录开发者工具
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg4tm8-0.png" alt="image-20221203212954956" style="zoom:50%;" />
|
||||
|
||||
创建小程序项目
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sm2eiy-0.png" alt="image-20221203213042020" style="zoom:67%;" />
|
||||
|
||||
熟悉开发者工具布局
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sm8s16-0.png" alt="image-20221203213108317" style="zoom:67%;" />
|
||||
|
||||
设置不校验合法域名
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/smlisf-0.png" alt="image-20221203213212370" style="zoom:67%;" />
|
||||
|
||||
**注:**开发阶段,小程序发出请求到后端的Tomcat服务器,若不勾选,请求发送失败。
|
||||
|
||||
|
||||
|
||||
### 入门案例
|
||||
|
||||
实际上,小程序的开发本质上属于前端开发,主要使用JavaScript开发,咱们现在的定位主要还是在后端,所以,对于小程序开发简单了解即可。
|
||||
|
||||
#### 小程序目录结构
|
||||
|
||||
小程序包含一个描述整体程序的 app 和多个描述各自页面的 page。一个小程序主体部分由三个文件组成,必须放在项目的根目录,如下:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/smppmq-0.png" alt="image-20221203220557676" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
**文件说明:**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/smtcpa-0.png" alt="image-20221203220635867" style="zoom:67%;" />
|
||||
|
||||
**app.js:**必须存在,主要存放小程序的逻辑代码
|
||||
|
||||
**app.json:**必须存在,小程序配置文件,主要存放小程序的公共配置
|
||||
|
||||
**app.wxss:** 非必须存在,主要存放小程序公共样式表,类似于前端的CSS样式
|
||||
|
||||
对小程序主体三个文件了解后,其实一个小程序又有多个页面。比如说,有商品浏览页面、购物车的页面、订单支付的页面、商品的详情页面等等。那这些页面会放在哪呢?
|
||||
会存放在pages目录。
|
||||
|
||||
每个小程序页面主要由四个文件组成:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg395d-0.png" alt="image-20221203220826893" style="zoom:50%;" />
|
||||
|
||||
**文件说明:**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3hq4-0.png" alt="image-20221203220839187" style="zoom:50%;" />
|
||||
|
||||
**js文件:**必须存在,存放页面业务逻辑代码,编写的js代码。
|
||||
|
||||
**wxml文件:**必须存在,存放页面结构,主要是做页面布局,页面效果展示的,类似于HTML页面。
|
||||
|
||||
**json文件:**非必须,存放页面相关的配置。
|
||||
|
||||
**wxss文件:**非必须,存放页面样式表,相当于CSS文件。
|
||||
|
||||
|
||||
|
||||
#### 编写和编译小程序
|
||||
|
||||
**1). 编写**
|
||||
|
||||
进入到index.wxml,编写页面布局
|
||||
|
||||
```xml
|
||||
<view class="container">
|
||||
<view>{{msg}}</view>
|
||||
<view>
|
||||
<button type="default" bindtap="getUserInfo">获取用户信息</button>
|
||||
<image style="width: 100px;height: 100px;" src="{{avatarUrl}}"></image>
|
||||
{{nickName}}
|
||||
</view>
|
||||
<view>
|
||||
<button type="primary" bindtap="wxlogin">微信登录</button>
|
||||
授权码:{{code}}
|
||||
</view>
|
||||
<view>
|
||||
<button type="warn" bindtap="sendRequest">发送请求</button>
|
||||
响应结果:{{result}}
|
||||
</view>
|
||||
</view>
|
||||
```
|
||||
|
||||
进入到index.js,编写业务逻辑代码
|
||||
|
||||
```javascript
|
||||
Page({
|
||||
data:{
|
||||
msg:'hello world',
|
||||
avatarUrl:'',
|
||||
nickName:'',
|
||||
code:'',
|
||||
result:''
|
||||
},
|
||||
getUserInfo:function(){
|
||||
wx.getUserProfile({
|
||||
desc: '获取用户信息',
|
||||
success:(res) => {
|
||||
console.log(res)
|
||||
this.setData({
|
||||
avatarUrl:res.userInfo.avatarUrl,
|
||||
nickName:res.userInfo.nickName
|
||||
})
|
||||
}
|
||||
})
|
||||
},
|
||||
wxlogin:function(){
|
||||
wx.login({
|
||||
success: (res) => {
|
||||
console.log("授权码:"+res.code)
|
||||
this.setData({
|
||||
code:res.code
|
||||
})
|
||||
}
|
||||
})
|
||||
},
|
||||
sendRequest:function(){
|
||||
wx.request({
|
||||
url: 'http://localhost:8080/user/shop/status',
|
||||
method:'GET',
|
||||
success:(res) => {
|
||||
console.log("响应结果:" + res.data.data)
|
||||
this.setData({
|
||||
result:res.data.data
|
||||
})
|
||||
}
|
||||
})
|
||||
}})
|
||||
```
|
||||
|
||||
|
||||
|
||||
**2). 编译**
|
||||
|
||||
点击编译按钮
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3fzg-0.png" alt="image-20221204181233015" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**3). 运行效果**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3efk-0.png" alt="image-20221204181606927" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
点击**获取用户信息**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3g33-0.png" alt="image-20221204182056440" style="zoom: 67%;" />
|
||||
|
||||
|
||||
|
||||
点击**微信登录**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3d01-0.png" alt="image-20221204182238762" style="zoom: 67%;" />
|
||||
|
||||
|
||||
|
||||
点击**发送请求**
|
||||
|
||||
因为请求http://localhost:8080/user/shop/status,先要启动后台项目。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3e6m-0.png" alt="image-20221204192519728" style="zoom: 67%;" />
|
||||
|
||||
**注:**设置不校验合法域名,若不勾选,请求发送失败。
|
||||
|
||||
|
||||
|
||||
#### 发布小程序
|
||||
|
||||
小程序的代码都已经开发完毕,要将小程序发布上线,让所有的用户都能使用到这个小程序。
|
||||
|
||||
点击上传按钮:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3edv-0.png" alt="image-20221204225355015" style="zoom:50%;" />
|
||||
|
||||
指定版本号:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3dl2-0.png" alt="image-20221204225502698" style="zoom:50%;" />
|
||||
|
||||
上传成功:
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3d7x-0.png" alt="image-20221204225557820" style="zoom:50%;" />
|
||||
|
||||
把代码上传到微信服务器就表示小程序已经发布了吗?
|
||||
**其实并不是。**当前小程序版本只是一个开发版本。
|
||||
|
||||
进到微信公众平台,打开版本管理页面。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3dk6-0.png" alt="image-20221204230231476" style="zoom:50%;" />
|
||||
|
||||
需提交审核,变成审核版本,审核通过后,进行发布,变成线上版本。
|
||||
|
||||
一旦成为线上版本,这就说明小程序就已经发布上线了,微信用户就可以在微信里面去搜索和使用这个小程序了。
|
||||
|
||||
|
||||
|
||||
## 微信登录
|
||||
|
||||
### 导入小程序代码
|
||||
|
||||
开发微信小程序,本质上是属于前端的开发,我们的重点其实还是后端代码开发。所以,小程序的代码已经提供好了,直接导入到微信开发者工具当中,直接来使用就可以了。
|
||||
|
||||
**1). 找到资料**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3hhg-0.png" alt="image-20221204205429798" style="zoom: 67%;" />
|
||||
|
||||
|
||||
|
||||
**2). 导入代码**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3bgu-0.png" alt="image-20221204205631809" style="zoom:50%;" />
|
||||
|
||||
AppID:使用自己的AppID
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3gdx-0.png" alt="image-20221204210011364" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**3). 查看项目结构**
|
||||
|
||||
主体的文件:app.js app.json app.wxss
|
||||
项目的页面比较多,主要存放在pages目录。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3bvh-0.png" alt="image-20221204210739195" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**4). 修改配置**
|
||||
|
||||
因为小程序要请求后端服务,需要修改为自己后端服务的ip地址和端口号(默认不需要修改)
|
||||
|
||||
common-->vendor.js-->搜索(ctrl+f)-->baseUri
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3ech-0.png" alt="image-20221204211239035" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
### 微信登录流程
|
||||
|
||||
微信登录:https://developers.weixin.qq.com/miniprogram/dev/framework/open-ability/login.html
|
||||
|
||||
**流程图:**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3du1-0.png" alt="image-20221204211800753" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**步骤分析:**
|
||||
|
||||
1. 小程序端,调用wx.login()获取code,就是授权码。
|
||||
2. 小程序端,调用wx.request()发送请求并携带code,请求开发者服务器(自己编写的后端服务)。
|
||||
3. 开发者服务端,通过HttpClient向微信接口服务发送请求,并携带appId+appsecret+code三个参数。
|
||||
4. 开发者服务端,接收微信接口服务返回的数据,session_key+opendId等。opendId是微信用户的唯一标识。
|
||||
5. 开发者服务端,自定义登录态,生成令牌(token)和openid等数据返回给小程序端,方便后绪请求身份校验。
|
||||
6. 小程序端,收到自定义登录态,存储storage。
|
||||
7. 小程序端,后绪通过wx.request()发起业务请求时,携带token。
|
||||
8. 开发者服务端,收到请求后,通过携带的token,解析当前登录用户的id。
|
||||
9. 开发者服务端,身份校验通过后,继续相关的业务逻辑处理,最终返回业务数据。
|
||||
|
||||
|
||||
|
||||
接下来,我们使用Postman进行测试。
|
||||
|
||||
**说明:**
|
||||
|
||||
1. 调用 [wx.login()](https://developers.weixin.qq.com/miniprogram/dev/api/open-api/login/wx.login.html) 获取 **临时登录凭证code** ,并回传到开发者服务器。
|
||||
2. 调用 [auth.code2Session](https://developers.weixin.qq.com/miniprogram/dev/api-backend/open-api/login/auth.code2Session.html) 接口,换取 **用户唯一标识 OpenID** 、 用户在微信开放平台帐号下的**唯一标识UnionID**(若当前小程序已绑定到微信开放平台帐号) 和 **会话密钥 session_key**。
|
||||
3. code是临时的,同一个用户,同一个小程序中,使用不同的code,可以获得唯一的openid!
|
||||
|
||||
之后开发者服务器可以根据用户标识来生成自定义登录态,用于后续业务逻辑中前后端交互时识别用户身份。
|
||||
|
||||
**实现步骤:**
|
||||
|
||||
**1). 获取授权码**
|
||||
|
||||
点击确定按钮,获取授权码,每个授权码只能使用一次,每次测试,需重新获取。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3nkv-0.png" alt="image-20221204222008130" style="zoom: 67%;" />
|
||||
|
||||
|
||||
|
||||
**2). 明确请求接口**
|
||||
|
||||
请求方式、请求路径、请求参数
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3j9x-0.png" alt="image-20221204222434054" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**3). 发送请求**
|
||||
|
||||
获取session_key和openid
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3mlq-0.png" alt="image-20221204223956568" style="zoom:50%;" />
|
||||
|
||||
若出现code been used错误提示,说明授权码已被使用过,请重新获取
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/sg3pj1-0.png" alt="image-20221204224130409" style="zoom:50%;" />
|
||||
|
||||
### 需求分析和设计
|
||||
|
||||
#### 产品原型
|
||||
|
||||
用户进入到小程序的时候,微信授权登录之后才能点餐。需要获取当前微信用户的相关信息,比如昵称、头像等,这样才能够进入到小程序进行下单操作。是基于微信登录来实现小程序的登录功能,没有采用传统账户密码登录的方式。若第一次使用小程序来点餐,就是一个新用户,需要把这个新的用户保存到数据库当中完成自动注册。
|
||||
|
||||
**登录功能原型图:**
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/swrbf2-0.png" alt="image-20221205173711304" style="zoom:50%;" />
|
||||
|
||||
|
||||
|
||||
**业务规则:**
|
||||
|
||||
- 基于微信登录实现小程序的登录功能
|
||||
- 如果是新用户需要自动完成注册
|
||||
|
||||
|
||||
|
||||
#### 接口设计
|
||||
|
||||
通过微信登录的流程,如果要完成微信登录的话,最终就要获得微信用户的openid。在小程序端获取授权码后,向后端服务发送请求,并携带授权码,这样后端服务在收到授权码后,就可以去请求微信接口服务。最终,后端向小程序返回openid和token等数据。
|
||||
|
||||
基于上述的登录流程,就可以设计出该接口的**请求参数**和**返回数据**。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/22/swrcfp-0.png" alt="image-20221205175429394" style="zoom:50%;" /> <img src="D:/folder/study/黑马程序员/苍穹外卖/讲义/讲义/day06/assets/image-20221205175441256.png" alt="image-20221205175441256" style="zoom:50%;" />
|
||||
|
||||
**说明:**请求路径/user/user/login,第一个user代表用户端,第二个user代表用户模块。
|
||||
278
自学/苍穹外卖.md
278
自学/苍穹外卖.md
@ -1176,7 +1176,7 @@ Controller 层和 Service 层的方法命名可根据不同业务场景进行区
|
||||
Mapper 执行动态 SQL,将已填充的字段写入数据库
|
||||
```
|
||||
|
||||
3). 在 需要统一填充的Mapper 的方法上加入 AutoFill 注解
|
||||
3). 在 需要统一填充的**Mapper 的方法上**加入 AutoFill 注解
|
||||
|
||||
|
||||
|
||||
@ -1184,268 +1184,6 @@ Mapper 执行动态 SQL,将已填充的字段写入数据库
|
||||
|
||||
|
||||
|
||||
## Java中操作Redis
|
||||
|
||||
### 环境搭建
|
||||
|
||||
进入到sky-server模块
|
||||
|
||||
**1). 导入Spring Data Redis的maven坐标(已完成)**
|
||||
|
||||
```java
|
||||
<dependency>
|
||||
<groupId>org.springframework.boot</groupId>
|
||||
<artifactId>spring-boot-starter-data-redis</artifactId>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
**2). 配置Redis数据源**
|
||||
|
||||
在application-dev.yml中添加
|
||||
|
||||
```java
|
||||
sky:
|
||||
redis:
|
||||
host: localhost
|
||||
port: 6379
|
||||
password: 123456
|
||||
database: 10
|
||||
```
|
||||
|
||||
**解释说明:**
|
||||
|
||||
database:指定使用Redis的哪个数据库,Redis服务启动后默认有16个数据库,编号分别是从0到15。
|
||||
|
||||
可以通过修改Redis配置文件来指定数据库的数量。
|
||||
|
||||
在application.yml中添加读取application-dev.yml中的相关Redis配置
|
||||
|
||||
```java
|
||||
spring:
|
||||
profiles:
|
||||
active: dev
|
||||
redis:
|
||||
host: ${sky.redis.host}
|
||||
port: ${sky.redis.port}
|
||||
password: ${sky.redis.password}
|
||||
database: ${sky.redis.database}
|
||||
```
|
||||
|
||||
**3). 编写配置类,创建RedisTemplate对象**
|
||||
|
||||
```java
|
||||
package com.sky.config;
|
||||
|
||||
import lombok.extern.slf4j.Slf4j;
|
||||
import org.springframework.context.annotation.Bean;
|
||||
import org.springframework.context.annotation.Configuration;
|
||||
import org.springframework.data.redis.connection.RedisConnectionFactory;
|
||||
import org.springframework.data.redis.core.RedisTemplate;
|
||||
import org.springframework.data.redis.serializer.StringRedisSerializer;
|
||||
|
||||
@Configuration
|
||||
@Slf4j
|
||||
public class RedisConfiguration {
|
||||
|
||||
@Bean
|
||||
public RedisTemplate redisTemplate(RedisConnectionFactory redisConnectionFactory){
|
||||
log.info("开始创建redis模板对象...");
|
||||
RedisTemplate redisTemplate = new RedisTemplate();
|
||||
//设置redis的连接工厂对象 连接工厂负责创建与 Redis 服务器的连接
|
||||
redisTemplate.setConnectionFactory(redisConnectionFactory);
|
||||
//设置redis key的序列化器 这意味着所有通过这个RedisTemplate实例存储的键都将被转换为字符串格式存储在Redis中
|
||||
redisTemplate.setKeySerializer(new StringRedisSerializer());
|
||||
return redisTemplate;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**解释说明:**
|
||||
|
||||
当前配置类不是必须的,因为 Spring Boot 框架会自动装配 RedisTemplate 对象,但是默认的key序列化器为
|
||||
|
||||
JdkSerializationRedisSerializer,**导致我们存到Redis中后的数据和原始数据有差别,故设置为**
|
||||
|
||||
**StringRedisSerializer序列化器**。
|
||||
|
||||
|
||||
|
||||
### 功能测试
|
||||
|
||||
**通过RedisTemplate对象操作Redis**
|
||||
|
||||
在test下新建测试类
|
||||
|
||||
**字符串测试**
|
||||
|
||||
```java
|
||||
@SpringBootTest
|
||||
public class SpringDataRedisTest {
|
||||
@Autowired
|
||||
private RedisTemplate redisTemplate;
|
||||
@Test
|
||||
public void testRedisTemplate(){
|
||||
System.out.println(redisTemplate);
|
||||
}
|
||||
@Test
|
||||
public void testString(){
|
||||
//set get setex setnx
|
||||
redisTemplate.opsForValue().set("city","北京");
|
||||
String city= (String) redisTemplate.opsForValue().get("city");
|
||||
System.out.println(city);
|
||||
redisTemplate.opsForValue().set("code","1234",3, TimeUnit.MINUTES); //设置code的值为1234,过期时间3min
|
||||
redisTemplate.opsForValue().setIfAbsent("lock","1"); //如果不存在该key则创建
|
||||
redisTemplate.opsForValue().setIfAbsent("lock","2");
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**哈希测试**
|
||||
|
||||
```java
|
||||
/**
|
||||
* 操作哈希类型的数据
|
||||
*/
|
||||
@Test
|
||||
public void testHash(){
|
||||
//hset hget hdel hkeys hvals
|
||||
HashOperations hashOperations = redisTemplate.opsForHash();
|
||||
|
||||
hashOperations.put("100","name","tom");
|
||||
hashOperations.put("100","age","20");
|
||||
|
||||
String name = (String) hashOperations.get("100", "name");
|
||||
System.out.println(name);
|
||||
|
||||
Set keys = hashOperations.keys("100");
|
||||
System.out.println(keys);
|
||||
|
||||
List values = hashOperations.values("100");
|
||||
System.out.println(values);
|
||||
|
||||
hashOperations.delete("100","age");
|
||||
}
|
||||
```
|
||||
|
||||
**get获得的是Object类型,keys获得的是set类型,values获得的是List**
|
||||
|
||||
|
||||
|
||||
**3). 操作列表类型数据**
|
||||
|
||||
```java
|
||||
/**
|
||||
* 操作列表类型的数据
|
||||
*/
|
||||
@Test
|
||||
public void testList(){
|
||||
//lpush lrange rpop llen
|
||||
ListOperations listOperations = redisTemplate.opsForList();
|
||||
|
||||
listOperations.leftPushAll("mylist","a","b","c");
|
||||
listOperations.leftPush("mylist","d");
|
||||
|
||||
List mylist = listOperations.range("mylist", 0, -1);
|
||||
System.out.println(mylist);
|
||||
|
||||
listOperations.rightPop("mylist");
|
||||
|
||||
Long size = listOperations.size("mylist");
|
||||
System.out.println(size);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**4). 操作集合类型数据**
|
||||
|
||||
```java
|
||||
/**
|
||||
* 操作集合类型的数据
|
||||
*/
|
||||
@Test
|
||||
public void testSet(){
|
||||
//sadd smembers scard sinter sunion srem
|
||||
SetOperations setOperations = redisTemplate.opsForSet();
|
||||
|
||||
setOperations.add("set1","a","b","c","d");
|
||||
setOperations.add("set2","a","b","x","y");
|
||||
|
||||
Set members = setOperations.members("set1");
|
||||
System.out.println(members);
|
||||
|
||||
Long size = setOperations.size("set1");
|
||||
System.out.println(size);
|
||||
|
||||
Set intersect = setOperations.intersect("set1", "set2");
|
||||
System.out.println(intersect);
|
||||
|
||||
Set union = setOperations.union("set1", "set2");
|
||||
System.out.println(union);
|
||||
|
||||
setOperations.remove("set1","a","b");
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**5). 操作有序集合类型数据**
|
||||
|
||||
```java
|
||||
/**
|
||||
* 操作有序集合类型的数据
|
||||
*/
|
||||
@Test
|
||||
public void testZset(){
|
||||
//zadd zrange zincrby zrem
|
||||
ZSetOperations zSetOperations = redisTemplate.opsForZSet();
|
||||
|
||||
zSetOperations.add("zset1","a",10);
|
||||
zSetOperations.add("zset1","b",12);
|
||||
zSetOperations.add("zset1","c",9);
|
||||
|
||||
Set zset1 = zSetOperations.range("zset1", 0, -1);
|
||||
System.out.println(zset1);
|
||||
|
||||
zSetOperations.incrementScore("zset1","c",10);
|
||||
|
||||
zSetOperations.remove("zset1","a","b");
|
||||
}
|
||||
```
|
||||
|
||||
**6). 通用命令操作**
|
||||
|
||||
|
||||
|
||||
- `*` 匹配零个或多个字符。
|
||||
- `?` 匹配任何单个字符。
|
||||
- `[abc]` 匹配方括号内的任一字符(本例中为 'a'、'b' 或 'c')。
|
||||
- `[^abc]` 或 `[!abc]` 匹配任何不在方括号中的单个字符。
|
||||
|
||||
```java
|
||||
/**
|
||||
* 通用命令操作
|
||||
*/
|
||||
@Test
|
||||
public void testCommon(){
|
||||
//keys exists type del
|
||||
Set keys = redisTemplate.keys("*");
|
||||
System.out.println(keys);
|
||||
|
||||
Boolean name = redisTemplate.hasKey("name");
|
||||
Boolean set1 = redisTemplate.hasKey("set1");
|
||||
|
||||
for (Object key : keys) {
|
||||
DataType type = redisTemplate.type(key);
|
||||
System.out.println(type.name());
|
||||
}
|
||||
|
||||
redisTemplate.delete("mylist");
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
## HttpClient
|
||||
|
||||
**HttpClient作用:**
|
||||
@ -1550,7 +1288,19 @@ public class HttpClientTest {
|
||||
|
||||
## 微信小程序
|
||||
|
||||
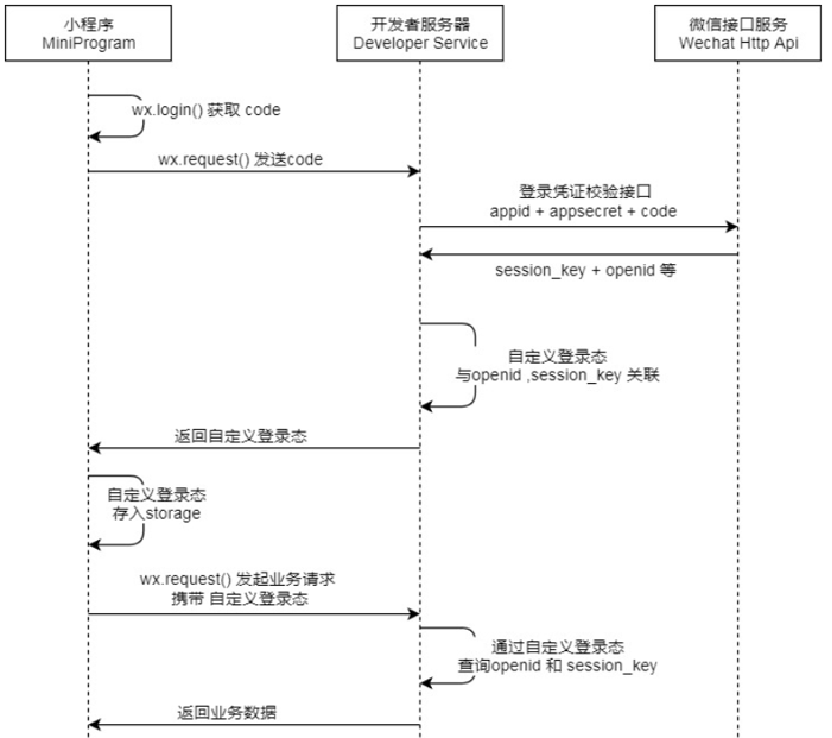
|
||||
<img src="https://pic.bitday.top/i/2025/03/19/u7y804-2.png" alt="image-20221204211800753" style="zoom:80%;" />
|
||||
|
||||
**步骤分析:**
|
||||
|
||||
1. 小程序端,调用wx.login()获取code,就是授权码。
|
||||
2. 小程序端,调用wx.request()发送请求并携带code,请求开发者服务器(自己编写的后端服务)。
|
||||
3. 开发者服务端,通过HttpClient向微信接口服务发送请求,并携带appId+appsecret+code三个参数。
|
||||
4. 开发者服务端,接收微信接口服务返回的数据,session_key+opendId等。opendId是微信用户的唯一标识。
|
||||
5. 开发者服务端,自定义登录态,生成令牌(token)和openid等数据返回给小程序端,方便后绪请求身份校验。
|
||||
6. 小程序端,收到自定义登录态,存储storage。
|
||||
7. 小程序端,后绪通过wx.request()发起业务请求时,携带token。
|
||||
8. 开发者服务端,收到请求后,通过携带的token,解析当前登录用户的id(无需获取openai,因为token中存了userid可以确认用户身份)。
|
||||
9. 开发者服务端,身份校验通过后,继续相关的业务逻辑处理,最终返回业务数据。
|
||||
|
||||
|
||||
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user