zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Commit on 2025/05/09 周五 21:39:37.74

Browse Source
This commit is contained in:
zhangsan 2025-05-09 21:39:37 +08:00
parent 7b566c5e8e
commit 6c517faa49
12 changed files with 1069 additions and 407 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

314
科研/ZY网络重构分析.md Normal file
View File

@ -0,0 +1,314 @@
如何确定kmeans的簇数？节点之间的流量，空间转为时间的图。
压缩感知 函数拟合 采样定理 傅里叶变换
## **谱分解**与网络重构
实对称矩阵性质：
对于任意 $n \times n$ 的实对称矩阵 $A$：
1. **秩可以小于 $n$**（即存在零特征值，矩阵不可逆）。
2. 但仍然有 $n$ 个线性无关的特征向量（即可对角化）。
一个实对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的**对称矩阵** $A$，
**完整谱分解**可以表示为：
$$
A = Q \Lambda Q^T \\
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T
$$
$Q$是$n \times n$的正交矩阵，每一列是一个特征向量；$\Lambda$是$n \times n$的对角矩阵，对角线元素是特征值$\lambda_i$ ，其余为0。
其中，$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值，$x_i$ 是对应的特征向量。
**事实上，如果矩阵 $A$ 的秩为 $r$ ,就只需要用前 $r$ 个特征值和特征向量就可以精确重构出。因为零特征值对矩阵重构不提供任何贡献。**
**截断的谱分解**（取前 r 个特征值和特征向量）
如果我们只保留前 $r$ 个最大的（或最重要的）特征值和对应的特征向量，那么：
- **特征向量矩阵 $U_r$**：取 $U$ 的前 $r$ 列，维度为 $n \times r$。
- **特征值矩阵 $\Lambda_r$**：取 $\Lambda$ 的前 $r \times r$ 子矩阵（即前 $r$ 个对角线元素），维度为 $r \times r$。
因此，截断后的近似分解为：
$$
A \approx U_r \Lambda_r U_r^T\\
A \approx \sum_{i=1}^{r} \lambda_i x_i x_i^T
$$
**推导过程**
1. **特征值和特征向量的定义**
对于一个对称矩阵 $A$，其特征值和特征向量满足：
$$
A x_i = \lambda_i x_i
$$
其中，$\lambda_i$ 是特征值，$x_i$ 是对应的特征向量。
2. **谱分解**
将这些特征向量组成一个正交矩阵 $Q$
$A = Q \Lambda Q^T$
$$
Q = \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix},
$$
$$
Q \Lambda = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix}.
$$
$$
Q \Lambda Q^T = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_n^T \end{bmatrix}.
$$
$$
Q \Lambda Q^T = \lambda_1 x_1 x_1^T + \lambda_2 x_2 x_2^T + \cdots + \lambda_n x_n x_n^T.
$$
可以写为
$$
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
$$
3. **网络重构**
在随机网络中，网络的邻接矩阵 $A$ 通常是对称的。利用预测算法得到的谱参数 $\{\lambda_i, x_i\}$ 后，就可以用以下公式重构网络矩阵：
$$
A(G) = \sum_{i=1}^{n} \lambda_i x_i x_i^T
$$
## 网络重构分析
### 基于扰动理论的特征向量估算方法
设原矩阵为 $A$，扰动后矩阵为 $A+\zeta C$（扰动矩阵 $\zeta C$，$\zeta$是小参数），令其第 $i$ 个特征值、特征向量分别为 $\lambda_i,x_i$ 和 $\tilde\lambda_i,\tilde x_i$。
**特征向量的一阶扰动公式：**
$$
\Delta x_i
=\tilde x_i - x_i
\;\approx\;
\zeta \sum_{k\neq i}
\frac{x_k^T\,C\,x_i}{\lambda_i - \lambda_k}\;x_k,
$$
- **输出**：对应第 $i$ 个特征向量修正量 $\Delta x_i$。
**特征值的一阶扰动公式：**
$$
\Delta\lambda_i = \tilde\lambda_i - \lambda_i \;\approx\;\zeta\,x_i^T\,C\,x_i
$$
**关键假设：**当扰动较小（ $\zeta\ll1$） 且各模态近似正交均匀时，常作进一步近似
$$
x_k^T\,C\,x_i \;\approx\; x_i^T\,C\,x_i \;
$$
正交： $\{x_k\}$ 本身是正交基，这是任何对称矩阵特征向量天然具有的属性。
均匀：我们把 $C$ 看作“**不偏向任何特定模态**”的随机小扰动——换句话说，投影到任何两个方向 $(x_i,x_k)$ 上的耦合强度 $x_k^T\,C\,x_i\quad\text{和}\quad x_i^T\,C\,x_i$ 在数值量级上应当差不多，因此可以互相近似。
因此，将所有的 $x_k^T C x_i$ 替换为 $x_i^T C x_i$：
$$
\Delta x_i \approx \zeta \sum_{k\neq i} \frac{x_i^T C x_i}{\lambda_i - \lambda_k} x_k = \zeta (x_i^T C x_i) \sum_{k\neq i} \frac{1}{\lambda_i - \lambda_k} x_k = \sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
$$
$$
\Delta x_i \approx\sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
$$
问题：
1. **当前时刻的邻接矩阵**
$$
A^{(1)}\in\mathbb R^{n\times n},\qquad
A^{(1)}\,x_i^{(1)}=\lambda_i^{(1)}\,x_i^{(1)},\quad \|x_i^{(1)}\|=1.
$$
2. **下一时刻的邻接矩阵**
$$
A^{(2)}\in\mathbb R^{n\times n},
$$
**已知**它的第 $i$ 个特征值 $\lambda_i^{(2)}$（卡尔曼滤波得来）. **求**当前时刻的特征向量 $x_i^{(2)}$。
**下一时刻**第 $i$ 个特征向量的预测为
$$
\boxed{
x_i^{(2)}
\;=\;
x_i^{(1)}+\Delta x_i
\;\approx\;
x_i^{(1)}
+\sum_{k\neq i}
\frac{\lambda_i^{(2)}-\lambda_i^{(1)}}
{\lambda_i^{(1)}-\lambda_k^{(1)}}\;
x_k^{(1)}.
}
$$
通过该估算方法可以依次求出下一时刻的所有特征向量。
### 矩阵符号说明
- 原始（真实）邻接矩阵：
$$
A = \sum_{m=1}^n \lambda_m\,x_m x_m^T,
\quad \lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n\;
$$
- 滤波估计得到的矩阵及谱分解：
$$
\widetilde A = \sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
\quad \widetilde\lambda_1\ge\cdots\ge\widetilde\lambda_n\;
$$
- 只取前 $r$ 项重构 ：
$$
A_r \;=\;\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
$$
- 对 $A_r$ 进行K-means聚类，得到 $A_{final}$
目标是让 $A_{final}$ = $A$
### **0/1矩阵**
其中 $\widetilde{\lambda}_i$ 和 $\widetilde{x}_i$ 分别为通过预测得到矩阵 $\widetilde A$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差，直接进行矩阵重构会使得重构误差较大。 对于这个问题，文献提出一种 0/1 矩阵近似恢复算法。
$$
a_{ij} =
\begin{cases}
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
0, & \text{else}
\end{cases}
$$
只要我们的估计值与真实值之间差距**小于 0.5**，就能保证阈值处理以后准确地恢复原边信息。
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
真实矩阵 $A$ 与预测矩阵 $\widetilde{A} $ 之间的差为
$$
A - \widetilde{A}=\sum_{m=1}^n \lambda_m\,x_m x_m^T-\sum_{m=1}^n \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T
$$
若假设特征向量扰动可忽略，即$\widetilde x_m\approx x_m$ ，扰动可简化为（这里可能有问题，特征向量的扰动也要计算）
$$
A - \widetilde{A} = \sum_{m=1}^n \Delta \lambda_m \widetilde{x}_m \widetilde{x}_m^T.
$$
对于任意元素 $(i, j)$ 上有
$$
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^n \Delta \lambda_m (\widetilde{x}_m \widetilde{x}_m^T)_{ij} \right| < \frac{1}{2}
$$
于一个归一化的特征向量 $\widetilde{x}_m$，其外积矩阵 $\widetilde{x}_m \widetilde{x}_m^T$ 的元素理论上满足
$$
|(\widetilde{x}_m \widetilde{x}_m^T)_{ij}| \leq 1.
$$
经过分析推导可以得出发生特征扰动时，网络精准重构条件为：
$$
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
$$
$$
\Delta {\lambda} < \frac{1}{2n}
$$
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比，网络中节点数量越多，实现精准重构的要求也就越高。
如果在**高层次**（特征值滤波）的误差累积超过了一定阈值，就有可能在**低层次**（邻接矩阵元素）中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5，就可以保证0-1矩阵的精确重构。
### **非0/1矩阵**
#### **全局误差度量**
对估计矩阵 $\widetilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类，得到中心 $\{c_k\}_{k=1}^K$。
- **簇内平均偏差**：
$$
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
$$
- **全局允许误差**：
$$
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
$$
#### 带权重构需控制两类误差：
1. **截断谱分解误差**$\epsilon$：
$$
\epsilon
= \bigl\|\widetilde A - A_r\bigr\|_F
= \Bigl\|\sum_{m=r+1}^n \widetilde\lambda_m\,\widetilde x_m \widetilde x_m^T\Bigr\|_F.
$$
---
2. **滤波误差**$\eta$：
**来源**：滤波器在谱域对真实特征值/向量的估计偏差，包括
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
- 特征向量：矩阵扰动得来
$$
A - \widetilde A=\sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
$$
$$
\eta \approx \Bigl\|\sum_{m=1}^n \Delta\lambda_m\,\widetilde x_m\widetilde x_m^T\Bigr\|_F
$$
#### **最终约束条件**：
$$
\boxed{
\underbrace{\eta}_{\text{滤波误差}}
\;+\;
\underbrace{\epsilon}_{\text{谱分解截断误差}}
\;\le\;
\underbrace{\delta_{\max}}_{\text{聚类量化容限}}
}
$$
量化的间隔是不是就和分布有关，有无其他影响因素。
通信原理，采样量化。
压缩感知的话量化分隔不是均匀的。
假设都是破松分布

45
科研/zy.md
View File

@ -4,6 +4,49 @@
流量单位时间内的流量
gat有没有问题 比如初始训练好的w和a 后面新加入节点 这个w和a不变会不会导致问题？ 我现在能实时重构出邻接矩阵a和特征矩阵 是否有帮助？ 是否也能替换与邻居节点的通信 因为卡尔曼能重构，知道邻居节点的特征？
若有中心服务器，可以保存全局0/1邻接矩阵A+带权邻接矩阵+特征矩阵H，周围节点通信一次即可获取全局信息
无中心服务器，每个节点可以获取0/1邻接矩阵A+带权邻接矩阵
实时重构出邻接矩阵a和权重矩阵 是否有帮助？ 带权邻接矩阵-》特征矩阵？ TGAT或EvolveGCN进行推理？
带权邻接矩阵仅作为边特征，特征矩阵？
社交网络中邻居关系，节点特征是不断变化的，可以利用TGAT或EvolveGCN进行预测，那么就要用已有训练集。但是不适合仿真使用，仿真是基于节点移动模型的。
关键假设：假设历史真实数据已知 可以拟合 二次函数 当作当前的测量值 因为我们要做实时估计 可能来不及获取实时值 但可以拟合过去的
或者直接谱分解上一个时刻重构的矩阵，得到特征值和特征向量序列 加上随机扰动作为观测输入
证明特征值稳定性： 网络平均度+高飞证明+gpt+实验。
需要解决的问题：确定Kmeans簇数、选取的特征值特征向量的维数。
先研究0-1矩阵
我现在有一个真实对称矩阵A，只有0-1元素，我对它的特征值和特征向量进行估计，可以得到n个特征值和特征向量，重构出 $\widetilde{A}$，但是我只选择了前r个特征值和特征向量进行谱分解重构，可以得到A_r，最后我对A_r使用kmeans量化的方法，得到A_final簇数为2，怎么进行误差分析，确定我这里的r,使得我最终得到的A_final可以满足精确重构A的要求。 这里可以假定得到n个特征值和特征向量这里的误差为\eta
特征值误差分析（方差）直接看李振河的，滤波误差看郭款
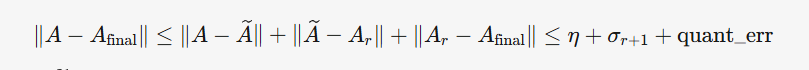
![image-20250509130405739](https://pic.bitday.top/i/2025/05/09/lkf38j-0.png)
$A-\tilde A$这里是滤波误差，是否包括特征值误差和**特征向量误差**？

341
科研/动态图神经网络.md
View File

@ -129,6 +129,7 @@ $$
Z_t = \text{Summarize}(H_t^{(l)}, d')
$$
将会舍弃部分节点
**实现方式**（论文方案）：
@ -150,17 +151,25 @@ $$
假设：
- 有3个节点（$n=3$），嵌入维度 $d=2$，选Top-2个节点（$d'=2$）。
- 节点嵌入：
$$ H_t^{(l)} = \begin{bmatrix} 1 & 0.5 \\ 0.3 & 2 \\ -1 & 1 \end{bmatrix}, \quad p = [1, 0] $$
$$
H_t^{(l)} = \begin{bmatrix} 1 & 0.5 \\ 0.3 & 2 \\ -1 & 1 \end{bmatrix}, \quad p = [1, 0]
$$
（$p$ 只关注嵌入的第一维，比如“用户发帖数量”）
1. **计算分数**：
$$ y_t = H_t^{(l)} p = [1 \cdot 1 + 0.5 \cdot 0, \ 0.3 \cdot 1 + 2 \cdot 0, \ -1 \cdot 1 + 1 \cdot 0] = [1, 0.3, -1] $$
$$
y_t = H_t^{(l)} p = [1 \cdot 1 + 0.5 \cdot 0, \ 0.3 \cdot 1 + 2 \cdot 0, \ -1 \cdot 1 + 1 \cdot 0] = [1, 0.3, -1]
$$
Top-2节点是第1、第2个节点（分数1和0.3）。
2. **加权聚合**：
$$ Z_t = \begin{bmatrix} [1, 0.5] \circ \tanh(1) \\ [0.3, 2] \circ \tanh(0.3) \end{bmatrix} = \begin{bmatrix} 0.76 & 0.38 \\ 0.09 & 0.58 \end{bmatrix} $$
2. **加权聚合**：
$$
Z_t = \begin{bmatrix} [1, 0.5] \circ \tanh(1) \\ [0.3, 2] \circ \tanh(0.3) \end{bmatrix} = \begin{bmatrix} 0.76 & 0.38 \\ 0.09 & 0.58 \end{bmatrix}
$$
（假设 $\tanh(1) \approx 0.76$, $\tanh(0.3) \approx 0.29$）
3. **输出**：$Z_t$ 是 $2 \times 2$ 矩阵，可以直接喂给GRU。
@ -171,7 +180,7 @@ $$
W_t^{(l)} = \text{GRU}(Z_t^T, W_{t-1}^{(l)})
$$
标准GRU，输入隐藏输出都是向量，这里都是矩阵！
标准GRU的输入、隐藏、输出都是向量，但这里都是矩阵！
当前时间步的输入：$Z_t^T$
@ -230,20 +239,20 @@ $$
1. **权重共享**：
- 所有时间步共享同一 GRU 的参数（$W_*, U_*, B_*$），确保模型尺寸不随时间增长。
2. **层独立性**：
- 每一层 GCN 的权重矩阵独立演化（不同层有各自的 GRU）。
- 每一层 GCN 的权重矩阵独立演化（不同层有各自的 GRU）。
3. **特征与结构的协同**：
- 节点嵌入 $H_t^{(l)}$ 既包含特征信息，也隐含历史结构信息（通过多层 GCN 传播），因此 GRU 能间接感知结构变化。
#### 6. 所需提前训练的权重
| **参数类型** | **符号** | **维度** | **作用** |
| ---------------- | --------------- | --------------------------- | ----------------------------- |
| GCN 初始权重 | $W_0^{(l)}$ | $\mathbb{R}^{d \times d'}$ | 初始时刻各层 GCN 的初始参数 |
| GRU 输入变换矩阵 | $W_Z, W_R, W_H$ | $\mathbb{R}^{d \times d'}$ | 将输入 $Z_t^T$ 映射到门控 |
| GRU 隐藏变换矩阵 | $U_Z, U_R, U_H$ | $\mathbb{R}^{d' \times d'}$ | 将 $W_{t-1}^{(l)}$ 映射到门控 |
| GRU 偏置项 | $B_Z, B_R, B_H$ | $\mathbb{R}^{d'}$ | 门控和候选状态的偏置 |
| Summarize 参数 | $p$ | $\mathbb{R}^d$ | 动态选择重要节点 |
| 任务相关参数 | 例如 MLP 权重 | 任务相关 | 链接预测、节点分类等输出层 |
| **参数类型** | **符号** | **维度** | **作用** |
| ---------------- | --------------- | --------------------------- | ------------------------------- |
| GCN 初始权重 | $W_0^{(l)}$ | $\mathbb{R}^{d \times d'}$ | 初始时刻各层 GCN 的初始参数 |
| GRU 输入变换矩阵 | $W_Z, W_R, W_H$ | $\mathbb{R}^{d \times d'}$ | 将输入 $Z_t^T$ 映射到门控 |
| GRU 隐藏变换矩阵 | $U_Z, U_R, U_H$ | $\mathbb{R}^{d' \times d'}$ | 将 $W_{t-1}^{(l)}$ 映射到门控 |
| GRU 偏置项 | $B_Z, B_R, B_H$ | $\mathbb{R}^{d'}$ | 门控和候选状态的偏置 |
| Summarize 参数 | $p$ | $\mathbb{R}^d$ | 对特征进行打分，不同层$p$不一样 |
| 任务相关参数 | 例如 MLP 权重 | 任务相关 | 链接预测、节点分类等输出层 |
@ -305,4 +314,302 @@ $H_t^{(l+1)} = \sigma(\widehat{A}_t H_t^{(l)} W_t^{(l)})$
## TGAT
## TGAT
### Bochner定理
Bochner定理为TGAT的**连续时间编码**提供了理论基础，使其能够将任意时间差映射为可学习的向量表示，从而在动态图中有效捕捉时序依赖。这一方法超越了传统离散编码的局限性，是TGAT的核心创新之一。
#### 时间编码的构造
**（1）Bochner 定理的数学形式**
根据Bochner定理，任意正定时间核函数 $ f(\Delta t) $ 可表示为：
$$
f(\Delta t) = \mathbb{E}_{\omega \sim \mu} \left[ e^{i \omega \Delta t} \right],
$$
其中 $e^{i \omega \Delta t} = \cos(\omega \Delta t) + i \sin(\omega \Delta t)$ 是复指数函数。
**（2）蒙特卡洛近似 & 实值化**
由于直接计算期望复杂，TGAT 用蒙特卡洛采样近似：
1. 从分布 $\mu$ 中采样 $k$ 个频率 $\omega_1, \omega_2, \ldots, \omega_k$。
2. 用这些频率构造实值编码（取复指数的实部和虚部，即 $\cos$ 和 $\sin$）：
$$
\phi(\Delta t) = \sqrt{\frac{1}{k}} \left[ \cos(\omega_1 \Delta t), \sin(\omega_1 \Delta t), \ldots, \cos(\omega_k \Delta t), \sin(\omega_k \Delta t) \right].
$$
这里 $k$ 是采样频率的数量，决定了编码的维度 $d=2k$（每组 $\cos + \sin$ 占 2 维）。
#### 例子
假设将时间$t$编码为一个2维向量（实际论文中维度更高，比如100维）。
时间编码函数为：
$$
\Phi_d(t) = \sqrt{\frac{1}{d}} \left[ \cos(\omega_1 t), \sin(\omega_1 t), \cos(\omega_2 t), \sin(\omega_2 t), \ldots \right]
$$
其中：
- $d$是维度（这里$d=2$，即2维向量）。
- $\omega_1, \omega_2, \ldots$ 是从某个分布$p(\omega)$中随机采样的频率参数（可以理解为“时间刻度”）。
1. **随机初始化频率**：
假设我们随机设定两个频率：
- $\omega_1 = 0.5$
- $\omega_2 = 1.0$
2. **编码时间点**：
- 对时间$t=2$，计算：
$$
\Phi_2(2) = \sqrt{\frac{1}{2}} \left[ \cos(0.5 \cdot 2), \sin(0.5 \cdot 2) \right] = \sqrt{0.5} \left[ \cos(1.0), \sin(1.0) \right] \approx [0.54, 0.84]
$$
- 对时间$t=5$，计算：
$$
\Phi_2(5) = \sqrt{0.5} \left[ \cos(2.5), \sin(2.5) \right] \approx [-0.35, 0.94]
$$
3. **时间差异的体现**：
- 两个时间点$t=2$和$t=5$的编码向量不同，且它们的点积（相似度）会反映时间跨度$|5-2|=3$：
$$
\Phi_2(2) \cdot \Phi_2(5) \approx 0.54 \cdot (-0.35) + 0.84 \cdot 0.94 \approx 0.59
$$
- 如果$t=2$和$t=4$的编码点积更大，说明$\Delta t=2$比$\Delta t=3$的交互更相关。
#### **为什么这样设计？**
- **谐波基函数**：`cos(ωt)`和`sin(ωt)`是周期性函数，能捕捉时间的周期性模式（比如白天/夜晚的周期性行为，但不会强制引入周期性）。
- **内积反映时间差**：通过Bochner定理，两个时间编码的内积`Φ(t₁)·Φ(t₂)`近似于一个时间核函数`𝒦(t₁-t₂)`，时间差越小，内积越大（相似性越高）。
- **可学习性**：频率参数`{ωᵢ}`可以通过训练优化（例如让模型自动学习“短期交互”和“长期交互”的不同时间尺度）。
### 工作原理
#### 1.时间约束的邻居集合
**时间约束**：对于目标节点 $v_0$ 在时间 $t$，其邻居 $\mathcal{N}(v_0; t)$ 仅包含与 $v_0$ **在时间 $t$ 之前发生过交互的节点**（即 $t_i < t$）。
$$
\mathcal{N}(v_0; t) = \{ v_i \mid \exists (v_0, v_i, t_i) \in \mathcal{E}, t_i < t \}
$$
实际实现中，TGAT通过以下两种策略避免邻居集合无限膨胀：
（1）**固定时间窗口（Sliding Time Window）**
- 仅保留目标时间 $t$ 的最近 $\Delta T$ 时间内的交互节点（例如过去7天的邻居）。
- **数学表达**：
$$
\mathcal{N}(v_0; t) = \{ v_i \mid (v_0, v_i, t_i) \in \mathcal{E}, t - \Delta T \leq t_i < t \}
$$
（2）**邻居采样（Neighborhood Sampling）**
- 即使在一个时间窗口内，如果邻居数量过多（例如社交网络中的活跃用户），TGAT会随机采样固定数量的邻居（如最多20个）。
- 随机采样可行是因为**时间编码**和**注意力权重**会自动学习为近期交互分配更高权重。
#### 2.时间编码的邻居特征矩阵
$$
Z(t) = \left[ \tilde{h}_0^{(l-1)}(t) \| \Phi_{d_T}(0), \tilde{h}_1^{(l-1)}(t_1) \| \Phi_{d_T}(t-t_1), \ldots \right]^\top
$$
**输入**：
- 目标节点 $v_0$ 在时间 $t$ 的上一层特征：$\tilde{h}_0^{(l-1)}(t)$。
- 邻居节点 $v_i$ 在历史时间 $t_i$ 的特征：$\tilde{h}_1^{(l-1)}(t_1), \tilde{h}_2^{(l-1)}(t_2), \ldots$。
- 时间编码函数 $\Phi_{d_T}$：将时间差 $t-t_i$ 映射为向量
#### 3.注意力权重计算
通过Query-Key-Value机制计算邻居权重：
$$
\alpha_i = \text{softmax} \left( \frac{(q(t)^\top K_i(t))}{\sqrt{d_h}} \right), \quad q(t) = [Z(t)]_0 W_Q, \quad K_i(t) = [Z(t)]_i W_K
$$
- $q(t)$：目标节点的Query。
- $K_i(t)$：邻居节点的Key。
- **动态性**：权重 $\alpha_i$ 依赖当前时间 $t$ 和邻居交互时间 $t_i$。
#### 4.多头注意力聚合
$$
h(t) = \text{Attn}(q(t), K(t), V(t)) = \sum_{i=1}^N \alpha_i V_i(t), \quad V_i(t) = [Z(t)]_i W_V
$$
$V_i(t)$：邻居节点的Value，含时间编码的特征。
#### 5.节点嵌入更新
$$
\tilde{h}_0^{(l)}(t) = \text{FFN}(h(t) \| x_0)
$$
- $h(t)$：聚合后的邻居表示。
- $x_0$：目标节点的原始特征。
- **FFN**（Feed-Forward Network）：进一步融合时空信息。
**动态推理**：对任意新时间 $t$，只需输入当前邻接关系和节点特征，通过前向传播计算嵌入。
总结：每个节点，动态融合节点自身及其邻居在不同时间点的嵌入，其中这些嵌入都显式编码了时间信息。
不同层之间的嵌入维度可以不同，但同一层内所有时间步的嵌入维度必须保持一致。
每个节点运行的模型一样的。实时性。
节点是否需要交互（是否需要全局信息） //
不知道全局信息(只知道邻居) 训练出来的模型是否一样？（能否协同。）
#### **举例**
假设目标节点 $v_0$ 在时间 $t=10$ 需要聚合历史邻居，其中：
$t=10$时$v_0$的特征：$\tilde{h}_0(t=10)=[0.1, 0.2, 0.3, 0.4, 0.5]$
- 在时间 $t_1=8$，$v_0$ 与邻居 $\{v_{1}, v_{2}\}$ 交互。
- $v_1$ 的特征：$\tilde{h}_1(t=8) = [0.6, 0.7, 0.8, 0.9, 1.0]$
- $v_2$ 的特征：$\tilde{h}_2(t=8) = [0.2, 0.3, 0.4, 0.5, 0.6]$
- 在时间 $t_2=5$，$v_0$ 与邻居 $\{v_{3}\}$ 交互。
- $v_3$ 的特征：$\tilde{h}_3(t=5) = [1.1, 1.2, 1.3, 1.4, 1.5]$
**时间编码**（$d_T=2$, $\omega_1=1$）：
- $\Phi_{d_T}(10-8=2) = [\cos(2), \sin(2)] \approx [-0.42, 0.91]$
- $\Phi_{d_T}(10-5=5) = [\cos(5), \sin(5)] \approx [0.28, -0.96]$
- $\Phi_{d_T}(0) = [1, 0]$
**将每个邻居的特征与对应时间编码拼接：**
$$
Z(10) = \begin{bmatrix}
\tilde{h}_0(10) \| \Phi_{d_T}(0) \\
\tilde{h}_1(8) \| \Phi_{d_T}(2) \\
\tilde{h}_2(8) \| \Phi_{d_T}(2) \\
\tilde{h}_3(5) \| \Phi_{d_T}(5)
\end{bmatrix} = \begin{bmatrix}
0.1, 0.2, 0.3, 0.4, 0.5, 1, 0 \\
0.6, 0.7, 0.8, 0.9, 1.0, -0.42, 0.91 \\
0.2, 0.3, 0.4, 0.5, 0.6, -0.42, 0.91 \\
1.1, 1.2, 1.3, 1.4, 1.5, 0.28, -0.96
\end{bmatrix}_{4 \times 7}
$$
**注意力权重计算:**
**1.投影矩阵参数**（简化示例，设 $d_h = 3$,真实情况由训-练得来）：
$$
W_Q = W_K = \begin{bmatrix}
0.1 & 0.2 & 0.3 \\
0.4 & 0.5 & 0.6 \\
0.7 & 0.8 & 0.9 \\
1.0 & 1.1 & 1.2 \\
1.3 & 1.4 & 1.5 \\
0.2 & 0.3 & 0.4 \\
0.5 & 0.6 & 0.7
\end{bmatrix}_{7 \times 3}, \quad
W_V = \begin{bmatrix}
0.3 & 0.4 & 0.5 \\
0.6 & 0.7 & 0.8 \\
0.9 & 1.0 & 1.1 \\
1.2 & 1.3 & 1.4 \\
1.5 & 1.6 & 1.7 \\
0.1 & 0.2 & 0.3 \\
0.4 & 0.5 & 0.6
\end{bmatrix}_{7 \times 3}
$$
**2.计算 Query/Key/Value**：
- **Query**（目标节点 $v_0$）：
$$
q(10) = [Z(10)]_0 W_Q = [0.1, 0.2, 0.3, 0.4, 0.5, 1, 0] \cdot W_Q = [2.38, 2.76, 3.14]
$$
- **Keys**（邻居节点）：
$$
K(10) = [Z(10)]_{1:3} W_K = \begin{bmatrix}
0.6 & 0.7 & 0.8 & 0.9 & 1.0 & -0.42 & 0.91 \\
0.2 & 0.3 & 0.4 & 0.5 & 0.6 & -0.42 & 0.91 \\
1.1 & 1.2 & 1.3 & 1.4 & 1.5 & 0.28 & -0.96
\end{bmatrix} \cdot W_K = \begin{bmatrix}
3.22 & 3.68 & 4.14 \\
1.82 & 2.18 & 2.54 \\
4.18 & 4.64 & 5.10
\end{bmatrix}
$$
- **Values**（邻居节点）：
$$
V(10) = [Z(10)]_{1:3} W_V = \begin{bmatrix}
3.52 & 3.92 & 4.32 \\
2.12 & 2.42 & 2.72 \\
4.48 & 4.88 & 5.28
\end{bmatrix}
$$
**3.计算注意力权重**
- 计算未归一化分数（缩放因子 $\sqrt{d_h} = \sqrt{3} \approx 1.732$）：
$$
\text{scores} = \frac{q(10) K(10)^\top}{\sqrt{3}} = \frac{[2.38, 2.76, 3.14] \cdot \begin{bmatrix}3.22 & 1.82 & 4.18 \\ 3.68 & 2.18 & 4.64 \\ 4.14 & 2.54 & 5.10\end{bmatrix}}{1.732}\approx [18.46, 10.56, 21.40]
$$
- Softmax 归一化：
$$
\alpha = \text{softmax}([18.46, 10.56, 21.40]) = [2.4 \times 10^{-2}, 1.6 \times 10^{-5}, 0.976]
$$
**4.聚合邻居信息**
$$
h(10) = \sum_{i=1}^3 \alpha_i V_i = 0.024 \cdot \begin{bmatrix}3.52 \\ 3.92 \\ 4.32\end{bmatrix} + 1.6 \times 10^{-5} \cdot \begin{bmatrix}2.12 \\ 2.42 \\ 2.72\end{bmatrix} + 0.976 \cdot \begin{bmatrix}4.48 \\ 4.88 \\ 5.28\end{bmatrix}\approx [4.48, 4.88, 5.28]
$$
**5.节点嵌入更新**
**1.拼接操作**
$$
z=[h(10) \| x_0] = [4.48, 4.88, 5.28, 0.1, 0.2, 0.3, 0.4, 0.5]
$$
**2. FFN参数设置**
FFN 包含两层：
$$
\tilde{h}_0^{(l)}(10)=\text{FFN}(z) = \text{ReLU}(z W_0 + b_0) W_1 + b_1
$$
### 需提前训练的参数
| **参数名称** | **符号** | **维度** | **作用** | **来源模块** |
| -------------------- | ---------------------------- | ------------------------ | ------------------------------------------------------ | ----------------------------- |
| **时间编码频率参数** | $\omega_1, \ldots, \omega_d$ | $d \times 1$ | 控制时间编码的基频率，用于生成 $\Phi_{d_T}(t)$。 | 功能性时间编码（Bochner定理） |
| **Query投影矩阵** | $W_Q$ | $(d + d_T) \times d_h$ | 将目标节点特征和时间编码映射为Query向量。 | 自注意力机制 |
| **Key投影矩阵** | $W_K$ | $(d + d_T) \times d_h$ | 将邻居节点特征和时间编码映射为Key向量。 | 自注意力机制 |
| **Value投影矩阵** | $W_V$ | $(d + d_T) \times d_h$ | 将邻居节点特征和时间编码映射为Value向量。 | 自注意力机制 |
| **FFN第一层权重** | $W_0^{(l)}$ | $(d_h + d_0) \times d_f$ | 前馈网络的第一层线性变换，融合邻居聚合特征和原始特征。 | 前馈网络（FFN） |
| **FFN第一层偏置** | $b_0^{(l)}$ | $d_f \times 1$ | 第一层的偏置项。 | 前馈网络（FFN） |
| **FFN第二层权重** | $W_1^{(l)}$ | $d_f \times d$ | 前馈网络的第二层线性变换，生成最终节点表示。 | 前馈网络（FFN） |
| **FFN第二层偏置** | $b_1^{(l)}$ | $d \times 1$ | 第二层的偏置项。 | 前馈网络（FFN） |

2
科研/图神经网络.md
View File

@ -268,6 +268,8 @@ $$
## GAT
以下例子只汇聚了一阶邻居信息！
图注意力网络（GAT）中最核心的运算：**图注意力层**。它的基本思想是：
1. **线性变换**：先对每个节点的特征 $\mathbf{h}_i$ 乘上一个可学习的权重矩阵 $W$，得到变换后的特征 $W \mathbf{h}_i$。

56
科研/数学基础.md
View File

@ -1132,62 +1132,6 @@ $$
## **谱分解**与网络重构
一个对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的**对称矩阵** $A$，其谱分解可以表示为：
$$
A = Q \Lambda Q^T \\
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T
$$
其中，$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值，$x_i$ 是对应的特征向量。
**推导过程**
1. **特征值和特征向量的定义**
对于一个对称矩阵 $A$，其特征值和特征向量满足：
$$
A x_i = \lambda_i x_i
$$
其中，$\lambda_i$ 是特征值，$x_i$ 是对应的特征向量。
2. **谱分解**
将这些特征向量组成一个正交矩阵 $Q$
$A = Q \Lambda Q^T$
$$
Q = \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix},
$$
$$
Q \Lambda = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix}.
$$
$$
Q \Lambda Q^T = \begin{bmatrix} \lambda_1 x_1 & \lambda_2 x_2 & \cdots & \lambda_n x_n \end{bmatrix} \begin{bmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_n^T \end{bmatrix}.
$$
$$
Q \Lambda Q^T = \lambda_1 x_1 x_1^T + \lambda_2 x_2 x_2^T + \cdots + \lambda_n x_n x_n^T.
$$
可以写为
$$
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
$$
3. **网络重构**
在随机网络中，网络的邻接矩阵 $A$ 通常是对称的。利用预测算法得到的谱参数 $\{\lambda_i, x_i\}$ 后，就可以用以下公式重构网络矩阵：
$$
A(G) = \sum_{i=1}^{n} \lambda_i x_i x_i^T
$$
## 幂迭代
幂迭代方法是一种常用的数值迭代算法，主要用于计算矩阵的**主特征值**（即具有最大模长的特征值）及其对应的**特征向量**。

63
科研/草稿.md
View File

@ -1,58 +1,35 @@
### **Bochner定理（Bochner's Theorem）简介**
Bochner定理是**调和分析（Harmonic Analysis）**中的一个重要定理，由数学家Salomon Bochner提出。它描述了**连续正定函数（positive definite functions）**与**非负有限测度（non-negative finite measures）**之间的对偶关系，在信号处理、概率论和机器学习（如核方法、时间编码）中有广泛应用。
以下是修改后的 Markdown 格式内容，公式用 `$` 或 `$$` 包裹：
---
### **1. 数学定义与公式**
Bochner定理的核心内容是：
> **一个连续函数 $ f: \mathbb{R}^d \to \mathbb{C} $ 是正定的（positive definite），当且仅当它是某个非负有限测度 $ \mu $ 的傅里叶变换。**
2. **截断的谱分解（取前 $r$ 个特征值和特征向量）**
数学表达式为：
$$
f(\mathbf{t}) = \int_{\mathbb{R}^d} e^{i \boldsymbol{\omega}^\top \mathbf{t}} \, \mathrm{d}\mu(\boldsymbol{\omega}),
$$
其中：
- $ \mathbf{t} \in \mathbb{R}^d $ 是输入向量（如时间差、空间坐标等）。
- $ \boldsymbol{\omega} $ 是频率域变量，$ \mu(\boldsymbol{\omega}) $ 是频域上的非负测度（可理解为能量分布）。
- $ e^{i \boldsymbol{\omega}^\top \mathbf{t}} $ 是复指数函数（傅里叶基）。
如果我们只保留前 $r$ 个最大的（或最重要的）特征值和对应的特征向量，那么：
#### **关键点**
- **正定函数**：满足对任意 $ n $ 个点 $ \mathbf{t}_1, \ldots, \mathbf{t}_n $，矩阵 $ [f(\mathbf{t}_i - \mathbf{t}_j)]_{i,j} $ 是半正定（positive semi-definite）的。
- **测度 $ \mu $**：代表频域的权重分布，可通过采样或优化学习得到。
- **特征向量矩阵 $U_r$**：取 $U$ 的前 $r$ 列，维度为 $n \times r$。
- **特征值矩阵 $\Lambda_r$**：取 $\Lambda$ 的前 $r \times r$ 子矩阵（即前 $r$ 个对角线元素），维度为 $r \times r$。
因此，截断后的近似分解为：
$$A \approx U_r \Lambda_r U_r^T$$
---
### **2. 在TGAT论文中的应用**
TGAT论文利用Bochner定理设计**功能性时间编码（Functional Time Encoding）**，将时间差 $ \Delta t $ 映射为向量表示。具体步骤：
### 修改说明：
1. 行内公式用 `$...$` 包裹（如 `$r$`, `$n \times r$`）。
2. 独立公式用 `$$...$$` 包裹（如最后的近似分解公式）。
3. 保留原文的列表结构和强调标记（`**`）。
4. 统一了中文标点（如冒号使用全角 `：`）。
#### **（1）时间编码的构造**
根据Bochner定理，任意正定时间核函数 $ f(\Delta t) $ 可表示为：
$$
f(\Delta t) = \mathbb{E}_{\omega \sim \mu} \left[ e^{i \omega \Delta t} \right],
$$
其中 $ \mu $ 是频率 $ \omega $ 的分布。通过蒙特卡洛采样近似：
$$
f(\Delta t) \approx \frac{1}{k} \sum_{j=1}^k e^{i \omega_j \Delta t}, \quad \omega_j \sim \mu.
$$
#### **（2）实值化处理**
由于神经网络需实数输入，取实部并拆分为正弦和余弦函数：
$$
\phi(\Delta t) = \sqrt{\frac{1}{k}} \left[ \cos(\omega_1 \Delta t), \sin(\omega_1 \Delta t), \ldots, \cos(\omega_k \Delta t), \sin(\omega_k \Delta t) \right].
$$
这构成了TGAT中时间差 $ \Delta t $ 的编码向量。
#### **优势**
- **理论保障**：Bochner定理确保时间编码的数学合理性（正定性保持拓扑结构）。
- **灵活性**：通过调整 $ \mu $ 可适应不同时间尺度模式。
以下是修改后的 Markdown 格式内容，公式用 `$$` 包裹：
---
### **3. 与其他方法的对比**
- **传统位置编码（如Transformer的PE）**：仅适用于离散序列，无法泛化到任意时间差。
- **Bochner编码**：适用于连续时间域，且能通过学习 $ \mu $ 优化时间敏感性。
$$A(G) = \sum_{i=1}^n \lambda_i x_i x_i^T$$
---
### **总结**
Bochner定理为TGAT的**连续时间编码**提供了理论基础，使其能够将任意时间差映射为可学习的向量表示，从而在动态图中有效捕捉时序依赖。这一方法超越了传统离散编码的局限性，是TGAT的核心创新之一。
### 说明：
1. 这是一个独立的数学公式，因此使用 `$$...$$` 包裹实现居中显示
2. 保持了原公式的所有数学符号和结构
3. 如果需要在行内使用，可以改为 `$...$` 包裹

34
科研/郭款论文.md
View File

@ -525,15 +525,16 @@ $$
2. 不断“旋转” $B$（乘以酉矩阵 $Q$）并对负值做截断，从而让最终的 $U$ 既接近 $B$ 又满足非负性。
这相当于把一部分“逼近”工作用特征分解先做了，然后只用旋转矩阵 $Q$ 来调整局部负值，再配合 $\max(0,\cdot)$ 截断满足非负约束。
**矩阵分解的重构算法步骤为：**
1. **输入**
- 预测特征向量矩阵 $X$
- 特征值矩阵 $\Lambda$
**矩阵重构算法步骤为：**
1. **输入** 由卡尔曼滤波预测得来！
- 预测特征向量矩阵 $X \in \mathbb{R}^{n \times r}$
- 特征值矩阵 $\Lambda \in \mathbb{R}^{r \times r}$
2. **初始化**
$$
B = X \Lambda^{\frac{1}{2}}, \quad Q = I, \quad U = \text{rand}(n, r)
B = X \Lambda^{\frac{1}{2}}, \quad Q = I, \quad U = max(0,B) ，\varepsilon
$$
3. **交替更新 $U$, $Q$**
@ -555,16 +556,15 @@ $$
$$
A' = U U^T
$$
并通过后续 FCM 算法进行聚类
7. **输出嵌入矩阵**
7. **输出精确重构矩阵**
对$A'$中各元素通过后续 FCM 算法进行聚类量化。
假设我们有一个 $2 \times 2$ 对称非负矩阵
**例：假设我们有一个 $2 \times 2$ 对称非负矩阵**
$$
A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}.
$$
@ -719,9 +719,19 @@ $V$ 和 $H$ 是 $r \times r$。
$\mathcal{O}(r^3)$
(3)重构A
$A \approx U U^T.$
$\mathcal{O}(n^2 r)$
(3) 由于通常 $n \gg r$，$\mathcal{O}(n r^2)$ 是主导项，故总复杂度（其中 $T$ 为迭代次数）
$$
T \cdot \mathcal{O}(nr^2)
{O}(n^2 r+Tn r^2)
$$

76
科研/颜佳佳论文.md
View File

@ -2,80 +2,6 @@
## 多智能体随机网络结构的实时精确估算
### 基于扰动理论的特征向量估算方法
设原矩阵为 $A$，扰动后矩阵为 $A+\zeta C$（扰动矩阵 $\zeta C$，$\zeta$是小参数），令其第 $i$ 个特征值、特征向量分别为 $\lambda_i,x_i$ 和 $\tilde\lambda_i,\tilde x_i$。
**特征向量的一阶扰动公式：**
$$
\Delta x_i
=\tilde x_i - x_i
\;\approx\;
\zeta \sum_{k\neq i}
\frac{x_k^T\,C\,x_i}{\lambda_i - \lambda_k}\;x_k,
$$
- **输出**：对应第 $i$ 个特征向量修正量 $\Delta x_i$。
**特征值的一阶扰动公式：**
$$
\Delta\lambda_i = \tilde\lambda_i - \lambda_i \;\approx\;\zeta\,x_i^T\,C\,x_i
$$
**关键假设：**当扰动较小（ $\zeta\ll1$） 且各模态近似正交均匀时，常作进一步近似
$$
x_k^T\,C\,x_i \;\approx\; x_i^T\,C\,x_i \;
$$
正交： $\{x_k\}$ 本身是正交基，这是任何对称矩阵特征向量天然具有的属性。
均匀：我们把 $C$ 看作“**不偏向任何特定模态**”的随机小扰动——换句话说，投影到任何两个方向 $(x_i,x_k)$ 上的耦合强度 $x_k^T\,C\,x_i\quad\text{和}\quad x_i^T\,C\,x_i$ 在数值量级上应当差不多，因此可以互相近似。
因此，将所有的 $x_k^T C x_i$ 替换为 $x_i^T C x_i$：
$$
\Delta x_i \approx \zeta \sum_{k\neq i} \frac{x_i^T C x_i}{\lambda_i - \lambda_k} x_k = \zeta (x_i^T C x_i) \sum_{k\neq i} \frac{1}{\lambda_i - \lambda_k} x_k = \sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
$$
$$
\Delta x_i \approx\sum_{k\neq i} \frac{\Delta \lambda_i}{\lambda_i - \lambda_k} x_k \tag{*}
$$
问题：
1. **当前时刻的邻接矩阵**
$$
A^{(1)}\in\mathbb R^{n\times n},\qquad
A^{(1)}\,x_i^{(1)}=\lambda_i^{(1)}\,x_i^{(1)},\quad \|x_i^{(1)}\|=1.
$$
2. **下一时刻的邻接矩阵**
$$
A^{(2)}\in\mathbb R^{n\times n},
$$
**已知**它的第 $i$ 个特征值 $\lambda_i^{(2)}$（卡尔曼滤波得来）. **求**当前时刻的特征向量 $x_i^{(2)}$。
**下一时刻**第 $i$ 个特征向量的预测为
$$
\boxed{
x_i^{(2)}
\;=\;
x_i^{(1)}+\Delta x_i
\;\approx\;
x_i^{(1)}
+\sum_{k\neq i}
\frac{\lambda_i^{(2)}-\lambda_i^{(1)}}
{\lambda_i^{(1)}-\lambda_k^{(1)}}\;
x_k^{(1)}.
}
$$
通过该估算方法可以依次求出下一时刻的所有特征向量。
### 多智能体随机网络特征值滤波建模
#### **1. 状态转移模型**
@ -93,8 +19,6 @@ $$
#### **2. 测量模型**
$v_k$
观测到的特征值向量 $z_k$ 为：
$$
z_k = \lambda_k + v_k

136
科研/高飞论文.md
View File

@ -228,142 +228,6 @@ $$
## 网络重构分析
### **0/1矩阵**
这里以n个特征值特征向量重构为例！
假设网络中有 $n$ 个节点，则矩阵 $A(G)$ 的维度为 $n \times n$，预测得到特征值和特征向量后，可以根据矩阵谱分解理论进行逆向重构网络邻接矩阵，表示如下：
$$
A(G) = \sum_{i=1}^n \hat{\lambda}_i \hat{x}_i \hat{x}_i^T
$$
其中 $\hat{\lambda}_i$ 和 $\hat{x}_i$ 分别为通过预测得到矩阵 $A(G)$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差，直接进行矩阵重构会使得重构误差较大。 对于这个问题，文献提出一种 0/1 矩阵近似恢复算法。
$$
a_{ij} =
\begin{cases}
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
0, & \text{else}
\end{cases}
$$
只要我们的估计值与真实值之间差距**小于 0.5**，就能保证阈值处理以后准确地恢复原边信息。
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
真实矩阵 $A(G)$ 与预测矩阵 $\hat{A}(G) $ 之间的差为
$$
A(G) - \hat{A}(G) = \sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
$$
对于任意元素 $(i, j)$ 上有
$$
\left| \sum_{m=1}^n \Delta \lambda_m (\hat{x}_m \hat{x}_m^T)_{ij} \right| = |a_{ij} - \hat{a}_{ij}| < \frac{1}{2}
$$
于一个归一化的特征向量 $\hat{x}_m$，其外积矩阵 $\hat{x}_m \hat{x}_m^T$ 的元素理论上满足
$$
|(\hat{x}_m \hat{x}_m^T)_{ij}| \leq 1.
$$
经过分析推导可以得出发生特征扰动时，网络精准重构条件为：
$$
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
$$
$$
\Delta {\lambda} < \frac{1}{2n}
$$
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比，网络中节点数量越多，实现精准重构的要求也就越高。
如果在**高层次**（特征值滤波）的误差累积超过了一定阈值，就有可能在**低层次**（邻接矩阵元素）中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5，就可以保证0-1矩阵的精确重构。
### **非0/1矩阵**
- 原始（真）加权邻接矩阵：
$$
A = \sum_{m=1}^n \lambda_m\,x_m x_m^T,
\quad \lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n,\;
x_m^T x_k=\delta_{mk}.
$$
- 估计得到的矩阵及谱分解：
$$
\widetilde A = \sum_{m=1}^n \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
\quad \widetilde\lambda_1\ge\cdots\ge\widetilde\lambda_n,\;
\widetilde x_m^T\widetilde x_k=\delta_{mk}.
$$
- 最终只取前 $r$ 项重构 ：
$$
A_r \;=\;\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
$$
#### **全局误差度量**
对估计矩阵 $\widetilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类，得到中心 $\{c_k\}_{k=1}^K$。
- **簇内平均偏差**：
$$
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
$$
- **全局允许误差**：
$$
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
$$
#### 带权重构需控制两类误差：
1. **谱分解截断误差**$\epsilon$：
$$
\epsilon
= \bigl\|\widetilde A - A_r\bigr\|_F
= \Bigl\|\sum_{m=r+1}^n \widetilde\lambda_m\,\widetilde x_m \widetilde x_m^T\Bigr\|_F.
$$
---
2. **滤波误差**$\eta$：
**来源**：滤波器在谱域对真实特征值/向量的估计偏差，包括
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
- 特征向量：矩阵扰动得来，不知道该不该算
$$
A - \widetilde A=\sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
$$
$$
\eta \approx \Bigl\|\sum_{m=1}^n \Delta\lambda_m\,\widetilde x_m\widetilde x_m^T\Bigr\|_F
$$
#### **最终约束条件**：
$$
\boxed{
\underbrace{\eta}_{\text{滤波误差}}
\;+\;
\underbrace{\epsilon}_{\text{谱分解截断误差}}
\;\le\;
\underbrace{\delta_{\max}}_{\text{聚类量化容限}}
}
$$
## 基于时空特征的节点位置预测
在本模型中，整个预测流程分为两大模块：

4
自学/Java笔记本.md
View File

@ -2003,11 +2003,11 @@ public class AnnotationTest4 {
public void save(EmployeeDTO employeeDTO) {
Employee employee = new Employee();
//对象属性拷贝
BeanUtils.copyProperties(employeeDTO, employee);
BeanUtils.copyProperties(employeeDTO, employee,"id");
}
```
employeeDTO的内容拷贝给employee
employeeDTO的内容拷贝给employee,跳过字段为"id"的属性。

87
自学/力扣Hot 100题.md
View File

@ -163,7 +163,7 @@ public class RandomDemo {
排序：
**排序：**
需要String先转为char [] 数组，排序好之后再转为String类型！！
@ -173,26 +173,35 @@ Arrays.sort(charArray);
String sortedStr = new String(charArray);
```
**iter遍历**,也要先转为char[]数组
```java
int[]cnt=new int[26];
for (Character c : s.toCharArray()) {
cnt[c-'a']++;
}
```
取字符：
**取字符：**
- `charAt(int index)` 方法返回指定索引处的 `char` 值。
- `char` 是基本数据类型，占用 2 个字节，表示一个 Unicode 字符。
- `HashSet<Character> set = new HashSet<Character>();`
取子串：
**取子串：**
- `substring(int beginIndex, int endIndex)` 方法返回从 `beginIndex` 到 `endIndex - 1` 的子字符串。
- 返回的是 `String` 类型，即使子字符串只有一个字符。
去除开头结尾空字符：
**去除开头结尾空字符：**
- `trim()`
分割字符串：
**分割字符串：**
**`split()`** 方法，可以用来分割字符串，并返回一个字符串数组。参数是正则表达式。
`split()` 方法，可以用来分割字符串，并返回一个字符串数组。参数是正则表达式。
```java
String str = "apple, banana, orange grape";
@ -200,6 +209,34 @@ String[] fruits = str.split(",\\s*"); // 按逗号后可能存在的空格分
// apple banana orange grape
```
仅用stringbuilder+substring:
```java
public static List<String> splitBySpace(String s) {
List<String> words = new ArrayList<>();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c != ' ') {
// 累积字母
sb.append(c);
} else {
// 遇到空格：如果 sb 里有内容，则构成一个单词
if (sb.length() > 0) {
words.add(sb.toString());
sb.setLength(0); // 清空，准备下一个单词
}
// 如果连续多个空格，则这里会跳过 sb.length()==0 的情况
}
}
// 循环结束后，sb 里可能还剩最后一个单词
if (sb.length() > 0) {
words.add(sb.toString());
}
return words;
}
```
### StringBuilder
@ -232,6 +269,7 @@ String[] fruits = str.split(",\\s*"); // 按逗号后可能存在的空格分
7.**`toString()`**
返回当前字符串缓冲区的内容，转换为 `String` 对象。
`sb.toString()`会创建并返回一个新的、独立的 `String` 对象，之后`setLength(0)`不会影响这个 `String` 对象
8.**`charAt(int index)`**
返回指定位置的字符。
@ -291,7 +329,7 @@ public class HashMapExample {
}
```
如何在创建的时候初始化？“双括号”初始化
**如何在创建的时候初始化？“双括号”初始化**
```
Map<Integer, Character> map = new HashMap<>() {{
@ -301,7 +339,7 @@ Map<Integer, Character> map = new HashMap<>() {{
}};
```
记录二维数组中某元素是否被访问过，推荐使用：
**记录二维数组中某元素是否被访问过，推荐使用：**
```java
int m = grid.length;
@ -314,6 +352,22 @@ visited[i][j] = true;
而非创建自定义Pair二元组作为键用Map记录。
**统计每个字母出现的次数：**
```java
int[] cnt = new int[26];
for (char c : magazine.toCharArray()) {
cnt[c - 'a']++;
}
```
**修改键值对中的键值：**
```java
Map<Character, Integer> counts = new HashMap<>();
counts.put(ch, counts.getOrDefault(ch, 0) + 1);
```
### HashSet
@ -359,6 +413,23 @@ visited[i][j] = true;
```java
public void isHappy() {
Set<Integer> set1 = new HashSet<>(List.of(1,2,3));
Set<Integer> set2 = new HashSet<>(List.of(2,3,1));
Set<Integer> set3 = new HashSet<>(List.of(3,2,1));
Set<Set<Integer>> sset = new HashSet<>();
sset.add(set1);
sset.add(set2);
sset.add(set3);
}
```
这里最终sset的size为1
### PriorityQueue
- 基于优先堆（最小堆或最大堆）实现，元素按优先级排序。

318
自学/苍穹外卖.md
View File

@ -1618,6 +1618,35 @@ cpolar.exe http 8080
### 百度地址解析
优化用户下单功能，加入校验逻辑，如果用户的收货地址距离商家门店超出配送范围（配送范围为5公里内），则下单失败。
思路：
​ 1. 基于百度地图开放平台实现（https://lbsyun.baidu.com/）
​ 2. 注册账号--->创建应用获取AK(服务端应用)--->调用接口
3. 相关接口
https://lbsyun.baidu.com/index.php?title=webapi/guide/webservice-geocoding
https://lbsyun.baidu.com/index.php?title=webapi/directionlite-v1
4. 商家门店地址可以配置在配置文件中，例如：
~~~yaml
sky:
shop:
address: 湖北省武汉市洪山区武汉理工大学
baidu:
ak: ${sky.baidu.ak}
~~~
## Spring Task
**Spring Task** 是Spring框架提供的任务调度工具，可以按照约定的时间自动执行某个代码逻辑。
@ -1626,7 +1655,7 @@ cpolar.exe http 8080
**作用：**定时自动执行某段Java代码
### 1.2 cron表达式
### cron表达式
**cron表达式**其实就是一个字符串，通过cron表达式可以**定义任务触发的时间**
@ -1634,29 +1663,71 @@ cpolar.exe http 8080
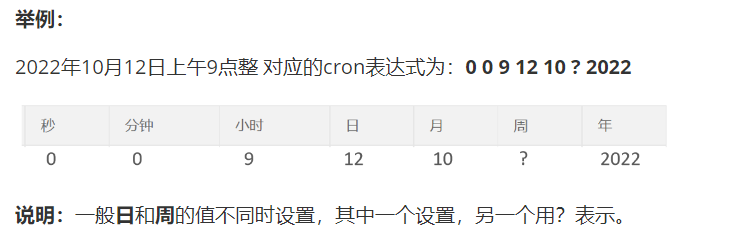
每个域的含义分别为：秒、分钟、小时、日、月、周、年(可选)
![image-20240807141614724](https://pic.bitday.top/i/2025/03/19/u7yh97-2.png)
<img src="https://pic.bitday.top/i/2025/03/19/u7yh97-2.png" alt="image-20240807141614724" style="zoom: 67%;" />
cron表达式在线生成器：https://cron.qqe2.com/
**通配符：**
\* 表示所有值；
? 表示未说明的值，即不关心它为何值；
\- 表示一个指定的范围；
, 表示附加一个可能值；
/ 符号前表示开始时间，符号后表示每次递增的值；
**cron表达式案例：**
*/5 * * * * ? 每隔5秒执行一次
0 0 5-15 * * ? 每天5-15点整点触发
0 0/3 * * * ? 每三分钟触发一次
0 0-5 14 * * ? 在每天下午2点到下午2:05期间的每1分钟触发
0 10/5 14 * * ? 在每天下午2点10分到下午2:55期间的每5分钟触发
0 0/30 9-17 * * ? 朝九晚五工作时间内每半小时
0 0 10,14,16 * * ? 每天上午10点，下午2点，4点
### 1.3 入门案例
**cron表达式在线生成器**：https://cron.qqe2.com/
#### 1.3.1 Spring Task使用步骤
现在可以直接GPT生成！
1). 导入maven坐标 spring-context（已存在）
### 入门案例
#### Spring Task使用步骤
1). 导入maven坐标 spring-context（Spring Boot Starter已包含）
<img src="https://pic.bitday.top/i/2025/03/19/u805dw-2.png" alt="image-20221218193251182" style="zoom:50%;" />
2). 启动类添加注解 @EnableScheduling 开启任务调度
3). 自定义定时任务类
3). 自定义定时任务类,然后只要在方法上标注 @Scheduled(cron = xxx)
```java
@Slf4j
@Component
public class MyTask {
//定时任务 每隔5秒触发一次
@Scheduled(cron = "0/5 * * * * ?")
public void executed(){
log.info("定時任務開始執行:{}",new Date());
}
}
```
### 2.订单状态定时处理
#### 2.1 需求分析
### 订单状态定时处理
用户下单后可能存在的情况：
@ -1670,51 +1741,6 @@ cron表达式在线生成器：https://cron.qqe2.com/
```java
@Component
@Slf4j
public class OrderTask {
/**
* 处理下单之后未15分组内支付的超时订单
*/
@Autowired
private OrderMapper orderMapper;
@Scheduled(cron = "0 * * * * ? ")
public void processTimeoutOrder(){
log.info("定时处理支付超时订单：{}", LocalDateTime.now());
LocalDateTime time = LocalDateTime.now().plusMinutes(-15);
// select * from orders where status = 1 and order_time < 当前时间-15分钟
List<Orders> ordersList = orderMapper.getByStatusAndOrdertimeLT(Orders.PENDING_PAYMENT, time);
if(ordersList != null && ordersList.size() > 0){
ordersList.forEach(order -> {
order.setStatus(Orders.CANCELLED);
order.setCancelReason("支付超时，自动取消");
order.setCancelTime(LocalDateTime.now());
orderMapper.update(order);
});
}
}
@Scheduled(cron = "0 0 1 * * ?")
public void processDeliveryOrder() {
log.info("处理派送中订单：{}", new Date());
// select * from orders where status = 4 and order_time < 当前时间-1小时
LocalDateTime time = LocalDateTime.now().plusMinutes(-60);
List<Orders> ordersList = orderMapper.getByStatusAndOrdertimeLT(Orders.DELIVERY_IN_PROGRESS, time);
if (ordersList != null && ordersList.size() > 0) {
ordersList.forEach(order -> {
order.setStatus(Orders.COMPLETED);
orderMapper.update(order);
});
}
}
}
```
## Websocket
WebSocket 是基于 TCP 的一种新的**网络协议**。它实现了浏览器与服务器全双工通信——浏览器和服务器只需要完成一次握手，两者之间就可以创建**持久性**的连接， 并进行**双向**数据传输。
@ -1727,22 +1753,149 @@ WebSocket 是基于 TCP 的一种新的**网络协议**。它实现了浏览器
- WebSocket支持**双向**通信
- HTTP和WebSocket底层都是TCP连接
**工作流程：**
1.握手（Handshake）
- 客户端发起一个特殊的 HTTP 请求（带有 `Upgrade: websocket` 和 `Connection: Upgrade` 头）
- 服务端如果支持 WebSocket，则返回 HTTP 101 Switching Protocols，双方在同一个 TCP 连接上切换到 WebSocket 协议
2.数据帧交换
- 握手成功后，客户端和服务端可以互相推送（push）“数据帧”（Frame），不再有 HTTP 的请求／响应模型
3.关闭连接
- 任一端发送关闭控制帧（Close Frame），对方确认后关闭 TCP 连接
<img src="https://pic.bitday.top/i/2025/05/08/m3qkmg-0.png" alt="image-20221222184352573" style="zoom:67%;" />
**WebSocket应用场景：**
视频弹幕、实时聊天、体育实况更新、股票基金实时更新报价
### 入门案例
**实现步骤：**
1). 直接使用websocket.html页面作为WebSocket客户端
```text
http://localhost:8080/ws/12345
```
最主要的是建立websocket连接！
2). 导入WebSocket的maven坐标
```xml
<dependency>
<groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-starter-websocket</artifactId>
</dependency>
```
3). 导入WebSocket服务端组件WebSocketServer，用于和客户端通信（比较固定，建立连接、接收消息、关闭连接、发送消息）
```java
/**
* WebSocket服务
*/
@Component
@ServerEndpoint("/ws/{sid}")
public class WebSocketServer {
//存放会话对象
private static Map<String, Session> sessionMap = new HashMap();
/**
* 连接建立成功调用的方法
*/
@OnOpen
public void onOpen(Session session, @PathParam("sid") String sid) {
System.out.println("客户端：" + sid + "建立连接");
sessionMap.put(sid, session);
}
/**
* 收到客户端消息后调用的方法
*
* @param message 客户端发送过来的消息
*/
@OnMessage
public void onMessage(String message, @PathParam("sid") String sid) {
System.out.println("收到来自客户端：" + sid + "的信息:" + message);
}
/**
* 连接关闭调用的方法
*
* @param sid
*/
@OnClose
public void onClose(@PathParam("sid") String sid) {
System.out.println("连接断开:" + sid);
sessionMap.remove(sid);
}
/**
* 群发
*
* @param message
*/
public void sendToAllClient(String message) {
Collection<Session> sessions = sessionMap.values();
for (Session session : sessions) {
try {
//服务器向客户端发送消息
session.getBasicRemote().sendText(message);
} catch (Exception e) {
e.printStackTrace();
}
}
}
}
```
4). 导入配置类WebSocketConfiguration，注册WebSocket的服务端组件
它通过Spring的 `ServerEndpointExporter` 将使用 `@ServerEndpoint` 注解的类自动注册为WebSocket端点。这样，当应用程序启动时，所有带有 `@ServerEndpoint` 注解的类就会被Spring容器自动扫描并注册为WebSocket服务器端点，使得它们能够接受和处理WebSocket连接。
```java
/**
* WebSocket配置类，用于注册WebSocket的Bean
*/
@Configuration
public class WebSocketConfiguration {
@Bean
public ServerEndpointExporter serverEndpointExporter() {
return new ServerEndpointExporter();
}
}
```
作用：找到`@ServerEndpoint` 的类并注册到容器中。
5). 导入定时任务类WebSocketTask，定时向客户端推送数据
```java
@Component
public class WebSocketTask {
@Autowired
private WebSocketServer webSocketServer;
/**
* 通过WebSocket每隔5秒向客户端发送消息
*/
@Scheduled(cron = "0/5 * * * * ?")
public void sendMessageToClient() {
webSocketServer.sendToAllClient("这是来自服务端的消息：" + DateTimeFormatter.ofPattern("HH:mm:ss").format(LocalDateTime.now()));
}
}
```
这里可以改为来单提醒、催单提醒。
### 来单提醒
@ -1756,4 +1909,57 @@ WebSocket 是基于 TCP 的一种新的**网络协议**。它实现了浏览器
- type 为消息类型，1为来单提醒 2为客户催单
- orderId 为订单id
- content 为消息内容
## 数据展示与处理
### 数据展示
Apache ECharts 是一款基于 Javascript 的数据可视化图表库，提供直观，生动，可交互，可个性化定制的数据可视化图表。
官网地址：https://echarts.apache.org/zh/index.html
例：营业额统计
<img src="https://pic.bitday.top/i/2025/05/08/qxl46n-0.png" alt="image-20230101160812029" style="zoom:67%;" />
具体返回数据一般由前端来决定，前端展示图表，折线图对应数据是什么格式，是有固定的要求的。所以说，后端需要去适应前端，它需要什么格式的数据，后端就返回什么格式的数据。
### 导出数据到Excel
#### Apache POI
我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作。一般情况下，POI 都是用于操作 Excel 文件。
**Apache POI的maven坐标**
```xml
<dependency>
<groupId>org.apache.poi</groupId>
<artifactId>poi</artifactId>
<version>3.16</version>
</dependency>
<dependency>
<groupId>org.apache.poi</groupId>
<artifactId>poi-ooxml</artifactId>
<version>3.16</version>
</dependency>
```
**实现步骤：**
1). 设计Excel模板文件！
2). 查询近30天的运营数据
3). 将查询到的运营数据写入模板文件
```java
row = sheet.getRow(7 + i); //获取行
row.getCell(1).setCellValue(date.toString()); //获取该行的某列，并设值。
```
4). 通过输出流将Excel文件下载到客户端浏览器
<img src="https://pic.bitday.top/i/2025/05/08/r1mrz8-0.png" alt="image-20230131152610559" style="zoom:67%;" />