zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Commit on 2025/07/12 周六 17:58:58.13

Browse Source
This commit is contained in:
zhangsan 2025-07-12 17:58:58 +08:00
parent 109b75d54b
commit 759551ffa0
15 changed files with 1114 additions and 608 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

48
后端学习/JavaWeb——后端.md
View File

@ -789,8 +789,6 @@ java -Dserver.port=9000 -jar XXXXX.jar --server.port=10010
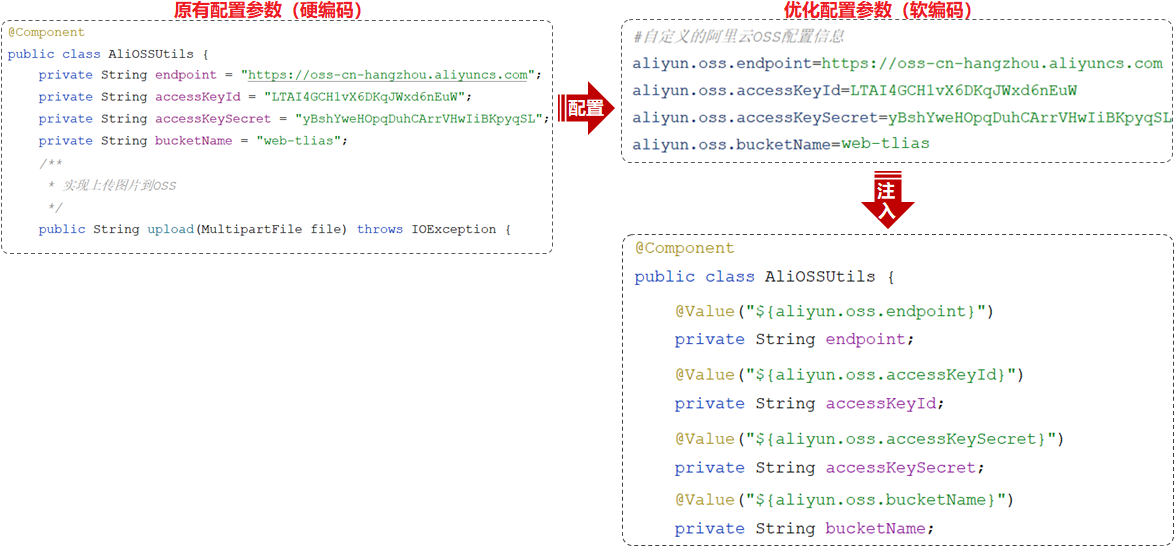
![image-20230102173905913](https://pic.bitday.top/i/2025/03/19/u6osck-2.png) ![image-20230102173905913](https://pic.bitday.top/i/2025/03/19/u6osck-2.png)
`@Value("${aliyun.oss.endpoint}")`
#### yml配置文件(推荐！！!) #### yml配置文件(推荐！！!)
@ -836,7 +834,7 @@ private List<String> hobby;
#### @ConfigurationProperties #### @ConfigurationProperties
是用来**将外部配置（如 `application.properties` / `application.yml`）映射到一个 POJO** 上的。 是用来**将外部配置（如 `application.yml`）映射到一个 POJO** 上的。
在 **Spring Boot** 中，根据 **驼峰命名转换**规则，自动将 `YAML` 配置文件中的 **键名**（例如 `user-token-name` `user_token_name`）映射到 **Java 类中的属性**（例如 `userTokenName`）。 在 **Spring Boot** 中，根据 **驼峰命名转换**规则，自动将 `YAML` 配置文件中的 **键名**（例如 `user-token-name` `user_token_name`）映射到 **Java 类中的属性**（例如 `userTokenName`）。
@ -866,7 +864,7 @@ Spring提供的简化方式套路：
4. (可选)引入依赖pom.xml （自动生成配置元数据，让 IDE **能识别并补全**你在 `application.properties/yml` 中的自定义配置项，提高开发体验，不加不影响运行！） 4. (可选)引入依赖pom.xml （自动生成配置元数据，让 IDE **能识别并补全**你在 `application.properties/yml` 中的自定义配置项，提高开发体验，不加不影响运行！）
```java ```xml
<dependency> <dependency>
<groupId>org.springframework.boot</groupId> <groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-configuration-processor</artifactId> <artifactId>spring-boot-configuration-processor</artifactId>
@ -875,6 +873,48 @@ Spring提供的简化方式套路：
#### 隐私数据配置
通常设置一个 `application-local.yml` 存放隐私数据，且加入 `.gitignore` ，表示仅存储在本地；然后`application.yml` 通过占位符引入该文件，eg:
application.yml
```yml
# 主配置文件，导入本地隐私文件，并通过占位符引用
spring:
config:
# Spring Boot 2.4+ 推荐用 import
import: optional:classpath:/application-local.yml
myapp:
datasource:
url: jdbc:mysql://localhost:3306/pay_mall
# 下面两个会从 application-local.yml 里拿
username: ${datasource.username}
password: ${datasource.password}
```
application-local.yml
```yml
# 本地专属配置，激活时才会加载
datasource:
username: root
password: 123456
```
这里有个松散绑定的原则，对于 `${datasource.username}` 这里匹配有效：
`userName username user-name user_name ` 这四个是等价的
底层做法是：
1. 全部字符转小写 → `username`
2. 去掉分隔符（`-`、`_`、`.`、空格） → `username`
3. 再匹配到 Java Bean 里的驼峰字段 `userName`（或直接 `username`，视你写的字段而定）
### Bean 的获取和管理 ### Bean 的获取和管理

508
后端学习/Java笔记本.md
View File

@ -353,264 +353,6 @@ for (MyObject obj : originalList) {
LocalDateTime.now()，获取当前时间 LocalDateTime.now()，获取当前时间
#### 访问修饰符
**public（公共的）**：
使用public修饰的成员可以被任何其他类访问，无论这些类是否属于同一个包。
例如，如果一个类的成员被声明为public，那么其他类可以通过该类的对象直接访问该成员。
**protected（受保护的）**：
使用protected修饰的成员可以被**同一个包**中的其他类访问，也可以被**不同包中的子类**访问。
与包访问级别相比，protected修饰符提供了更广泛的访问权限。
**default (no modifier)（默认的，即包访问级别）**：
如果没有指定任何访问修饰符，则默认情况下成员具有包访问权限。
在同一个包中的其他类可以访问默认访问级别的成员，但是在不同包中的类不能访问。
**private**（私有的）：
使用private修饰的成员只能在声明它们的**类内部**访问，其他任何类都不能访问这些成员。
这种访问级别提供了最高的封装性和安全性。
如果您在另一个类中实例化了包含私有成员的类，那么您无法直接访问该类的私有成员。但是，您可以通过**公共方法**来间接地访问和操作私有成员。
则每个实例都有自己的一份拷贝，只有当变量被声明为 static 时，变量才是类级别的，会被所有实例共享。
```java
// 文件：com/example/PrivateExample.java
package com.example;
public class PrivateExample {
private int privateVar = 30;
// 公共方法，用于访问私有成员
public int getPrivateVar() {
return privateVar;
}
}
```
修饰符不仅可以用来修饰成员变量和方法，也可以用来**修饰类**。顶级类只能使用 `public` 或默认（即不写任何修饰符，称为包访问权限）。内部类可以使用所有访问修饰符（`public`、`protected`、`private` 和默认），这使得你可以更灵活地控制嵌套类的访问范围。
```java
public class OuterClass {
// 内部类使用private，只能在OuterClass内部访问
private class InnerPrivateClass {
// ...
}
// 内部类使用protected，同包以及其他包中的子类可以访问
protected class InnerProtectedClass {
// ...
}
// 内部类使用默认访问权限，只在同包中可见
class InnerDefaultClass {
// ...
}
// 内部类使用public，任何地方都可访问（但访问时需要通过OuterClass对象）
public class InnerPublicClass {
// ...
}
}
```
#### 四种内部类
下面是四种内部类（成员内部类、局部内部类、静态内部类和匿名内部类）的示例代码，展示了如何用每一种方式来实现`Runnable`的`run()`方法并创建线程。
**1) 成员内部类**
定义位置：成员内部类定义在外部类的**成员位置**。
访问权限：可以无限制地访问外部类的所有成员，**包括私有成员**。
实例化方式：需要先创建外部类的实例，然后才能创建内部类的实例。
修改限制：不能有静态字段和静态方法（除非声明为常量`final static`）。**成员内部类属于外部类的一个实例，不能独立存在于类级别上。**
用途：适用于内部类与外部类关系密切，需要频繁访问外部类成员的情况。
```java
public class OuterClass {
class InnerClass implements Runnable {
// static int count = 0; // 编译错误
public static final int CONSTANT = 100; // 正确：可以定义常量
public void run() {
System.out.println("成员内部类中的线程正在运行...");
}
}
public void startThread() {
InnerClass inner = new InnerClass();
Thread thread = new Thread(inner);
thread.start();
}
public static void main(String[] args) {
OuterClass outer = new OuterClass();
outer.startThread();
}
}
```
**2.局部内部类**
定义位置：局部内部类定义在**一个方法或任何块内**（如：if语句、循环语句内）。
访问权限：只能访问**所在方法**的`final`或事实上的`final`（即不被后续修改的）局部变量和外部类的成员变量（同成员内部类）。
实例化方式：只能在定义它们的块中创建实例。
修改限制：同样不能有静态字段和方法。
用途：适用于只在方法或代码块中使用的类，有助于将实现细节隐藏在方法内部。
```java
public class OuterClass {
public void startThread() {
class LocalInnerClass implements Runnable {
public void run() {
System.out.println("局部内部类中的线程正在运行...");
}
}
LocalInnerClass localInner = new LocalInnerClass();
Thread thread = new Thread(localInner);
thread.start();
}
public static void main(String[] args) {
OuterClass outer = new OuterClass();
outer.startThread();
}
}
```
**3.静态内部类**
定义位置：定义在外部类内部，但使用`static`修饰。
访问权限：只能直接访问外部类的静态成员，访问非静态成员需要通过外部类实例。
实例化方式：**可以直接创建，不需要外部类的实例**。
修改限制：可以有自己的静态成员。
用途：适合当内部类工作不依赖外部类实例时使用，常用于实现与外部类关系不那么密切的帮助类。
```java
public class OuterClass {
// 外部类的静态成员
private static int staticVar = 10;
// 外部类的实例成员
private int instanceVar = 20;
// 静态内部类
public static class StaticInnerClass {
public void display() {
// 可以直接访问外部类的静态成员
System.out.println("staticVar: " + staticVar);
// 下面这行代码会报错，因为不能直接访问外部类的实例成员
// System.out.println("instanceVar: " + instanceVar);
// 如果确实需要访问实例成员，可以通过创建外部类的对象来访问
OuterClass outer = new OuterClass();
System.out.println("通过外部类实例访问 instanceVar: " + outer.instanceVar);
}
}
public static void main(String[] args) {
// 直接创建静态内部类的实例，不需要外部类实例
OuterClass.StaticInnerClass inner = new OuterClass.StaticInnerClass();
inner.display();
}
}
```
**4.匿名内部类**
**在定义的同时直接实例化**，而不需要显式地声明一个子类的名称。
定义位置：在需要使用它的地方立即**定义**和**实例化**。
访问权限：类似局部内部类，只能访问`final`或事实上的`final`局部变量。
实例化方式：在定义时就实例化，不能显式地命名构造器。
修改限制：不能有任何静态成员。
用途：适用于创建一次性使用的实例，通常用于**接口或抽象类**的实现。但**匿名内部类**并不限于接口或抽象类，只要是**非 `final` 的普通类**，都有机会通过匿名内部类来“现场”创建一个**它的子类实例**。
​
```java
abstract class Animal {
public abstract void makeSound();
}
public class Main {
public static void main(String[] args) {
// 匿名内部类：临时创建一个 Animal 的子类并实例化
Animal dog = new Animal() { // 注意这里的 new Animal() { ... }
@Override
public void makeSound() {
System.out.println("汪汪汪！");
}
};
dog.makeSound(); // 输出：汪汪汪！
}
}
```
如何理解？可以对比**普通子类（显式定义）**，即显示定义了**Dog**来继承Animal
```java
// 抽象类或接口
abstract class Animal {
public abstract void makeSound();
}
// 显式定义一个具名的子类
class Dog extends Animal {
@Override
public void makeSound() {
System.out.println("汪汪汪！");
}
}
public class Main {
public static void main(String[] args) {
// 实例化具名的子类
Animal dog = new Dog();
dog.makeSound(); // 输出：汪汪汪！
}
}
```
#### Lambda表达式 #### Lambda表达式
@ -1028,6 +770,74 @@ public class Dog {
#### 访问修饰符
**public（公共的）**：
使用public修饰的成员可以被任何其他类访问，无论这些类是否属于同一个包。
例如，如果一个类的成员被声明为public，那么其他类可以通过该类的对象直接访问该成员。
**protected（受保护的）**：
使用protected修饰的成员可以被**同一个包**中的其他类访问，也可以被**不同包中的子类**访问。
与包访问级别相比，protected修饰符提供了更广泛的访问权限。
**default (no modifier)（默认的，即包访问级别）**：
如果没有指定任何访问修饰符，则**默认情况下成员具有包访问权限**。
在同一个包中的其他类可以访问默认访问级别的成员，但是在不同包中的类不能访问。
**private**（私有的）：
使用private修饰的成员只能在声明它们的**类内部**访问，其他任何类（子类也不行！）都不能访问这些成员。
这种访问级别提供了最高的封装性和安全性。
如果您在另一个类中实例化了包含私有成员的类，那么您无法直接访问该类的私有成员。但是，您可以通过**公共方法**来间接地访问和操作私有成员。
```java
public class PrivateExample {
private int privateVar = 30;
// 公共方法，用于访问私有成员
public int getPrivateVar() {
return privateVar;
}
}
```
则每个实例都有自己的一份拷贝，只有当变量被声明为 static 时，变量才是类级别的，会被所有实例共享。
修饰符不仅可以用来修饰成员变量和方法，也可以用来**修饰类**。顶级类只能使用 `public` 或默认（即不写任何修饰符，称为包访问权限）。内部类可以使用所有访问修饰符（`public`、`protected`、`private` 和默认），这使得你可以更灵活地控制嵌套类的访问范围。
```java
public class OuterClass {
// 内部类使用private，只能在OuterClass内部访问
private class InnerPrivateClass {
// ...
}
// 内部类使用protected，同包以及其他包中的子类可以访问
protected class InnerProtectedClass {
// ...
}
// 内部类使用默认访问权限，只在同包中可见
class InnerDefaultClass {
// ...
}
// 内部类使用public，任何地方都可访问（但访问时需要通过OuterClass对象）
public class InnerPublicClass {
// ...
}
}
```
#### **JAVA**三大特性 #### **JAVA**三大特性
**封装** **封装**
@ -1274,6 +1084,188 @@ public class Main {
#### 四种内部类
下面是四种内部类（成员内部类、局部内部类、静态内部类和匿名内部类）的示例代码，展示了如何用每一种方式来实现`Runnable`的`run()`方法并创建线程。
**1) 成员内部类**
定义位置：成员内部类定义在外部类的**成员位置**。
访问权限：可以无限制地访问外部类的所有成员，**包括私有成员**。
实例化方式：需要先创建外部类的实例，然后才能创建内部类的实例。
修改限制：不能有静态字段和静态方法（除非声明为常量`final static`）。**成员内部类属于外部类的一个实例，不能独立存在于类级别上。**
用途：适用于内部类与外部类关系密切，需要频繁访问外部类成员的情况。
```java
public class OuterClass {
class InnerClass implements Runnable {
// static int count = 0; // 编译错误
public static final int CONSTANT = 100; // 正确：可以定义常量
public void run() {
System.out.println("成员内部类中的线程正在运行...");
}
}
public void startThread() {
InnerClass inner = new InnerClass();
Thread thread = new Thread(inner);
thread.start();
}
public static void main(String[] args) {
OuterClass outer = new OuterClass();
outer.startThread();
}
}
```
**2.局部内部类**
定义位置：局部内部类定义在**一个方法或任何块内**（如：if语句、循环语句内）。
访问权限：只能访问**所在方法**的`final`或事实上的`final`（即不被后续修改的）局部变量和外部类的成员变量（同成员内部类）。
实例化方式：只能在定义它们的块中创建实例。
修改限制：同样不能有静态字段和方法。
用途：适用于只在方法或代码块中使用的类，有助于将实现细节隐藏在方法内部。
```java
public class OuterClass {
public void startThread() {
class LocalInnerClass implements Runnable {
public void run() {
System.out.println("局部内部类中的线程正在运行...");
}
}
LocalInnerClass localInner = new LocalInnerClass();
Thread thread = new Thread(localInner);
thread.start();
}
public static void main(String[] args) {
OuterClass outer = new OuterClass();
outer.startThread();
}
}
```
**3.静态内部类**
定义位置：定义在外部类内部，但使用`static`修饰。
访问权限：只能直接访问外部类的静态成员，访问非静态成员需要通过外部类实例。
实例化方式：**可以直接创建，不需要外部类的实例**。
修改限制：可以有自己的静态成员。
用途：适合当内部类工作不依赖外部类实例时使用，常用于实现与外部类关系不那么密切的帮助类。
```java
public class OuterClass {
// 外部类的静态成员
private static int staticVar = 10;
// 外部类的实例成员
private int instanceVar = 20;
// 静态内部类
public static class StaticInnerClass {
public void display() {
// 可以直接访问外部类的静态成员
System.out.println("staticVar: " + staticVar);
// 下面这行代码会报错，因为不能直接访问外部类的实例成员
// System.out.println("instanceVar: " + instanceVar);
// 如果确实需要访问实例成员，可以通过创建外部类的对象来访问
OuterClass outer = new OuterClass();
System.out.println("通过外部类实例访问 instanceVar: " + outer.instanceVar);
}
}
public static void main(String[] args) {
// 直接创建静态内部类的实例，不需要外部类实例
OuterClass.StaticInnerClass inner = new OuterClass.StaticInnerClass();
inner.display();
}
}
```
**4.匿名内部类**
**在定义的同时直接实例化**，而不需要显式地声明一个子类的名称。
定义位置：在需要使用它的地方立即**定义**和**实例化**。
访问权限：类似局部内部类，只能访问`final`或事实上的`final`局部变量。
实例化方式：在定义时就实例化，不能显式地命名构造器。
修改限制：不能有任何静态成员。
用途：适用于创建一次性使用的实例，通常用于**接口或抽象类**的实现。但**匿名内部类**并不限于接口或抽象类，只要是**非 `final` 的普通类**，都有机会通过匿名内部类来“现场”创建一个**它的子类实例**。
​
```java
abstract class Animal {
public abstract void makeSound();
}
public class Main {
public static void main(String[] args) {
// 匿名内部类：临时创建一个 Animal 的子类并实例化
Animal dog = new Animal() { // 注意这里的 new Animal() { ... }
@Override
public void makeSound() {
System.out.println("汪汪汪！");
}
};
dog.makeSound(); // 输出：汪汪汪！
}
}
```
如何理解？可以对比**普通子类（显式定义）**，即显示定义了**Dog**来继承Animal
```java
// 抽象类或接口
abstract class Animal {
public abstract void makeSound();
}
// 显式定义一个具名的子类
class Dog extends Animal {
@Override
public void makeSound() {
System.out.println("汪汪汪！");
}
}
public class Main {
public static void main(String[] args) {
// 实例化具名的子类
Animal dog = new Dog();
dog.makeSound(); // 输出：汪汪汪！
}
}
```
### 容器 ### 容器

112
后端学习/Mybatis&-Plus.md
View File

@ -95,22 +95,7 @@ SQL注入：由于没有对用户输入进行充分检查，而SQL又是拼接
- ${...} - ${...}
- 拼接SQL。直接将参数拼接在SQL语句中，**存在SQL注入问题** - 拼接SQL。直接将参数拼接在SQL语句中，**存在SQL注入问题**
- 使用时机：如果对表名、列表进行动态设置时使用 - 使用时机：如果对**表名、列表**进行动态设置时使用
### 日志输出
只建议开发环境使用：在Mybatis当中我们可以借助日志，查看到sql语句的执行、执行传递的参数以及执行结果
1. 打开application.properties文件
2. 开启mybatis的日志，并指定输出到控制台
```java
#指定mybatis输出日志的位置, 输出控制台
mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
```
@ -125,7 +110,7 @@ mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
**大驼峰命名（UpperCamelCase）**： **大驼峰命名（UpperCamelCase）**：
- 每个单词的首字母都大写，通常用于类名或类型名。 - 每个单词的**首字母都大写**，通常用于类名或类型名。
- **例子**：`MyClass`, `EmployeeData`, `OrderDetails` - **例子**：`MyClass`, `EmployeeData`, `OrderDetails`
@ -155,25 +140,9 @@ mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
### 推荐的完整配置：
```yaml
mybatis:
#mapper配置文件
mapper-locations: classpath:mapper/*.xml
type-aliases-package: com.sky.entity
configuration:
#开启驼峰命名
map-underscore-to-camel-case: true
```
`type-aliases-package: com.sky.entity`把 `com.sky.entity` 包下的所有类都当作别名注册，XML 里就可以直接写 `<resultType="Dish">` 而不用写全限定名。可以多添加几个包，用逗号隔开。
### 增删改 ### 增删改
- **增删改通用！：返回值为int时，表示影响的记录数，一般不需要可以设置为void！** **增删改通用！：返回值为int时，表示影响的记录数，一般不需要可以设置为void！**
**作用于单个字段** **作用于单个字段**
@ -278,7 +247,7 @@ resultType属性，指的是查询返回的单条记录所封装的类型(查询
parameterType属性（可选，MyBatis 会根据接口方法的入参类型（比如 `Dish` 或 `DishPageQueryDTO`）自动推断），POJO作为入参，需要使用全类名或是`type‑aliases‑package: com.sky.entity` 下注册的别名。 parameterType属性（可选，MyBatis 会根据接口方法的入参类型（比如 `Dish` 或 `DishPageQueryDTO`）自动推断），POJO作为入参，需要使用全类名或是`type‑aliases‑package: com.sky.entity` 下注册的别名。
``` ```xml
<insert id="insert" useGeneratedKeys="true" keyProperty="id"> <insert id="insert" useGeneratedKeys="true" keyProperty="id">
<select id="pageQuery" resultType="com.sky.vo.DishVO"> <select id="pageQuery" resultType="com.sky.vo.DishVO">
<select id="list" resultType="com.sky.entity.Dish" parameterType="com.sky.entity.Dish"> <select id="list" resultType="com.sky.entity.Dish" parameterType="com.sky.entity.Dish">
@ -307,24 +276,55 @@ parameterType属性（可选，MyBatis 会根据接口方法的入参类型（
3. 编写查询语句 3. 编写查询语句
```xml ```xml
<select id="list" resultType="edu.whut.pojo.Emp"> <select id="findByName"
select * from emp parameterType="String"
where name like concat('%',#{name},'%') resultType="edu.whut.pojo.Emp">
and gender = #{gender} SELECT
and entrydate between #{begin} and #{end} id, name, gender, entrydate, update_time
order by update_time desc FROM emp
WHERE name = #{name}
</select> </select>
``` ```
**`id="list"`**：指定查询方法的名称，应该与 Mapper 接口中的方法名称一致。 **`id="list"`**：指定查询方法的名称，应该与 Mapper 接口中的方法名称一致。
**`resultType="edu.whut.pojo.Emp"`**：`resultType` 只在 **查询操作** 中需要指定。指定查询结果映射的对象类型，这里是 `Emp` 类。 **`resultType="edu.whut.pojo.Emp"`**：`resultType` 只在 **查询操作** 中需要指定。指定查询结果映射的对象类型，这里是 `Emp` 类。
这里有bug！！！ ### 推荐的完整配置
`concat('%',#{name},'%')`这里应该用`<where>` `<if>`标签对name是否为`NULL`或`''`进行判断 ```yaml
mybatis:
#mapper配置文件
mapper-locations: classpath:mapper/*.xml
type-aliases-package: com.sky.entity
configuration:
#开启驼峰命名
map-underscore-to-camel-case: true
log-impl: org.apache.ibatis.logging.stdout.StdOutImpl
```
`type-aliases-package: com.sky.entity`把 `com.sky.entity` 包下的所有类都当作别名注册，XML 里就可以直接写 `<resultType="Dish">` 而不用写全限定名。可以多添加几个包，用逗号隔开。
`log-impl:org.apache.ibatis.logging.stdout.StdOutImpl`只建议开发环境使用：在Mybatis当中我们可以借助日志，查看到sql语句的执行、执行传递的参数以及执行结果
`map-underscore-to-camel-case: true` 如果都是简单字段，开启之后XML 中**不用写** `<resultMap>`：
```xml
<resultMap id="dataMap" type="edu.whut.infrastructure.dao.po.PayOrder">
<id column="id" property="id"/>
<result column="user_id" property="userId"/>
<result column="product_id" property="productId"/>
<result column="product_name" property="productName"/>
</resultMap>
```
@ -363,6 +363,26 @@ parameterType属性（可选，MyBatis 会根据接口方法的入参类型（
**不加判空条件时**
- 如果 `name == null`，大多数数据库里 `CONCAT('%', NULL, '%')` 会返回 `NULL`，于是条件变成了 `WHERE name LIKE NULL`
- 如果 `name == ""`（空串），`CONCAT('%','', '%')` 得到 `"%%"`，`name LIKE '%%'` 对所有非null `name` 都成立，相当于“不过滤”这段条件。
**加了判空 `<if>` 之后**
```xml
<where>
<if test="name != null and name != ''">
AND name LIKE CONCAT('%', #{name}, '%')
</if>
<!-- 其它条件类似 -->
</where>
```
当 `name` 为 `null` 或 `""` 时，这段 `<if>` 块**不会**被拼到最终的 SQL 里，等价于**忽略**了 `name` 这个过滤条件。
#### SQL-foreach #### SQL-foreach
Mapper 接口 Mapper 接口
@ -371,7 +391,7 @@ Mapper 接口
@Mapper @Mapper
public interface EmpMapper { public interface EmpMapper {
//批量删除 //批量删除
public void deleteByIds(List<Integer> ids); public void deleteByIds(@Param("ids") List<Integer> ids);
} }
``` ```

9
后端学习/力扣Hot 100题.md
View File

@ -906,9 +906,16 @@ int[] partialArray = Arrays.copyOfRange(source, 1, 4); //复制指定元素，
int double 数值默认初始化为0，boolean默认初始化为false int double 数值默认初始化为0，boolean默认初始化为false
``` ```java
//一维
int[] memo = new int[nums.length]; int[] memo = new int[nums.length];
Arrays.fill(memo, -1); Arrays.fill(memo, -1);
//二维
int[][] test=new int[2][2];
for (int[] ints : test) {
Arrays.fill(ints,1);
}
``` ```

162
杂项/linux服务器.md
View File

@ -1239,3 +1239,165 @@ services:
``` ```
## 内网穿透
### 使用服务提供商
网址：https://natapp.cn
**1.隧道查看**
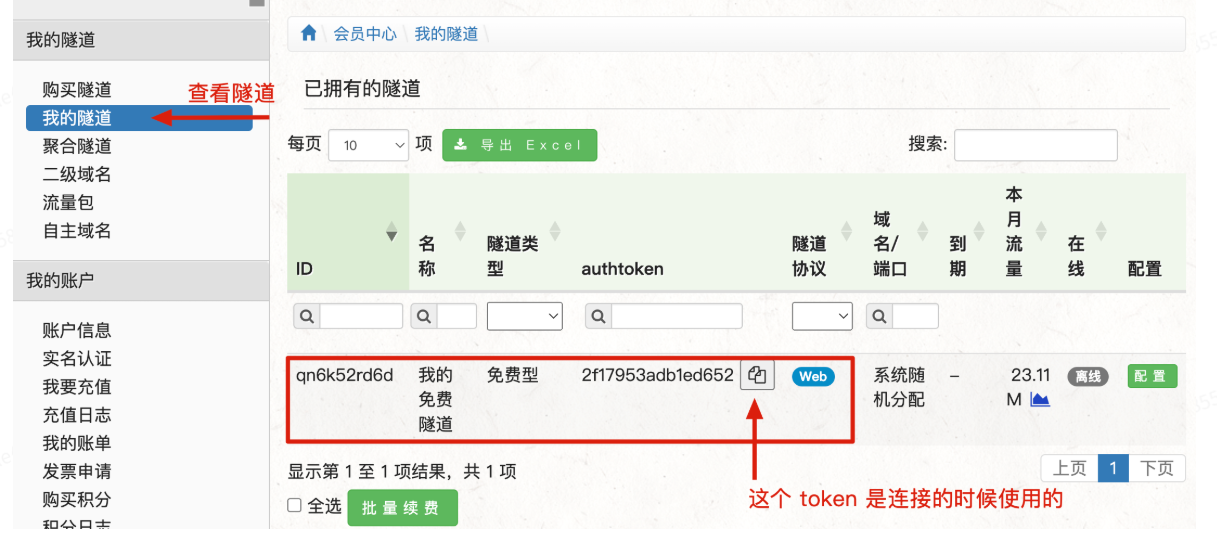
![image-20250711100420529](https://pic.bitday.top/i/2025/07/11/gluhqb-0.png)
**2.隧道配置**
配置映射关系：
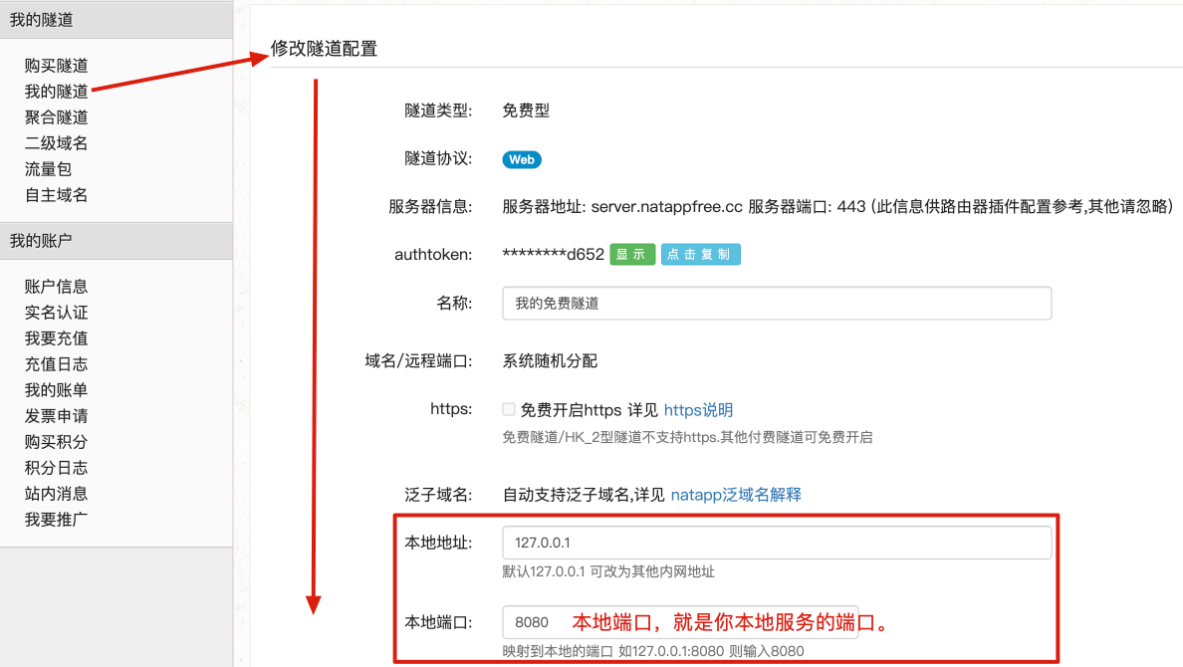
![image-20250711100440865](https://pic.bitday.top/i/2025/07/11/glx8n3-0.png)
**3.客户端下载与配置**
https://natapp.cn/#download ，参考官方文档，配置本地token，启动本地客户端。
## 自己搭建FRP
### 数据流转流程
**外部请求到达 frp-server**
- 你在 `frps.ini`（服务端配置）里为某个 proxy 分配了一个 `remote_port`（或 `custom_domains`）。
- 当外部用户（浏览器、移动端、其他服务）访问 `http://your.frps.ip:remote_port/...` 时，流量首先打到你部署在公网的 **frp-server** 上。
**frp-server 转发到 frp-client**
- frp-server 维护着一个与每个 frp-client 的**长连接**（control connection）。
- 收到外部连接后，frp-server 会基于这个 control 通道告诉对应的 frp-client：
> “有一个新连接，请你去拿 `proxy(name)` 对应的后端服务数据。”
- frp-server 不自己去连 Java 后端，它只是做信令和数据的“管道”管理。
**frp-client 建立到本地 Java 服务的连接**
- frp-client 收到信令后，内部根据 `proxies` 配置：
```toml
[[proxies]]
name = "my-java-app"
type = "tcp"
local_ip = "127.0.0.1"
local_port = 8080
remote_port= 18080
```
- 它会在容器或宿主机内部打开一个新的 TCP 连接，指向 `127.0.0.1:8080`（即你的 Java 服务）
### frp-server
frps.toml:
```toml
# https://github.com/fatedier/frp/blob/dev/conf/frps_full_example.toml
[common]
# 监听端口
bind_port = 7000
# 面板端口
dashboard_port = 7500
# 登录面板的账号密码（修改成自己的）
dashboard_user = admin
dashboard_pwd = admin
# token =
```
docker-compose:
```yml
version: '3.9'
services:
frps:
image: fatedier/frps:v0.60.0
hostname: frps
container_name: frps
volumes:
- "./config/frps.toml:/frps.toml"
command:
- "-c"
- "/frps.toml"
network_mode: "host"
```
### frp-client
frpc.toml:
```toml
# 服务端地址 https://github.com/fatedier/frp/blob/dev/conf/frpc_full_example.toml
serverAddr = "124.71.159.195"
# 服务端配置的bindPort
serverPort = 7000
# token =
[[proxies]]
# 代理应用名称，根据自己需要进行配置
name = "smile-dev-tech-01"
# 代理类型 有tcp\udp\stcp\p2p
type = "tcp"
# 客户端代理应用IP
localIP = "host.docker.internal"
# 客户端代理应用端口
localPort = 8234
# 服务端反向代理端口；提供给外部访问
remotePort = 8234
[[proxies]]
# 代理应用名称，根据自己需要进行配置
name = "smile-dev-tech-02"
# 代理类型 有tcp\udp\stcp\p2p
type = "tcp"
# 客户端代理应用IP
localIP = "host.docker.internal"
# 客户端代理应用端口
localPort = 9001
# 服务端反向代理端口；提供给外部访问
remotePort = 9001
```
docker-compose:
```yml
# 命令执行 docker-compose -f docker-compose.yml up -d
version: '3.9'
services:
frpc:
image: fatedier/frpc:v0.60.0
hostname: frpc
container_name: frpc
volumes:
- "./config/frpc.toml:/frpc.toml"
command:
- "-c"
- "/frpc.toml"
network_mode: "host"
```
frp-server必须部署在有公网ip的服务器，frp-client客户端有两种部署方式：
1.docker部署，如上
2.下载windows客户端https://github.com/fatedier/frp/releases/tag/v0.60.0
**注意：**如果java后端和client都部署在docker同一网络中，`frpc.toml` 中 `localIP = "localhost"`
如果client在docker容器，java在idea中启动，那么 `localIP = "host.docker.internal"`
如果client在windows下启动，java在idea中启动， `localIP = "localhost"`
总之，关键是让client和java互通；client和server互通比较容易！！！
公网ip:7500 可以查看面板。

75
科研/ZY网络重构分析.md
View File

@ -216,42 +216,67 @@ $$
设对称矩阵 设对称矩阵
$$ $$
A = \begin{bmatrix} 1 & 0 & 2 \\ 0 & -1 & 0 \\ 2 & 0 & 1 \end{bmatrix} A = \begin{bmatrix}
1 & 0 & 1 \\
0 & 0 & 0 \\
1 & 0 & -1
\end{bmatrix}
$$ $$
1. **特征分解** **特征分解**
- 特征值： - 特征值：
$$ \lambda_1 = 3, \quad \lambda_2 = -1, \quad \lambda_3 = 0 $$ $$ \lambda_1 = \sqrt{2}, \quad \lambda_2 = -\sqrt{2}, \quad \lambda_3 = 0 $$
- 特征向量矩阵： - 特征向量矩阵和特征值矩阵：
$$ $$
Q = \begin{bmatrix} Q = \begin{bmatrix}
\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1 + \sqrt{2}}{2} & \frac{1 - \sqrt{2}}{2} & 0 \\
0 & 1 & 0 \\ 0 & 0 & 1 \\
\frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \frac{1}{2} & \frac{1}{2} & 0
\end{bmatrix}, \quad
\Lambda = \begin{bmatrix}
\sqrt{2} & 0 & 0 \\
0 & -\sqrt{2} & 0 \\
0 & 0 & 0
\end{bmatrix} \end{bmatrix}
$$ $$
2. **构造SVD** **构造SVD**
- 步骤： 步骤：
1. 按 $|\lambda_i|$ 降序排列：$3, 1, 0$（取绝对值后排序）。 1. 按 $|\lambda_i|$ 降序排列：$\sigma_1 = \sqrt{2}, \sigma_2 = \sqrt{2}, \sigma_3 = 0$（取绝对值后排序）。
2. 奇异值矩阵： 2. 奇异值矩阵：
$$ \Sigma = \text{diag}(3, 1, 0) $$ $$\Sigma = \mathrm{diag}\bigl(\sqrt{2},\,\sqrt{2},\,0\bigr).$$
3. 符号调整矩阵： 3. 符号调整矩阵：
$$ S = \text{diag}(1, -1, 1) \quad (\lambda_3=0 \text{ 的符号可任选}) $$ $$
4. 左奇异向量矩阵： S = \mathrm{diag}\bigl(\operatorname{sign}(\lambda_1),\,\operatorname{sign}(\lambda_2),\,\operatorname{sign}(\lambda_3)\bigr)
$$ U = Q S = \begin{bmatrix} = \mathrm{diag}(+1,\,-1,\,+1),
\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ $$
0 & -1 & 0 \\ 4. 左奇异向量矩阵：
\frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} $$
\end{bmatrix} $$ U = Q\,S
5. 右奇异向量矩阵： = \begin{bmatrix}
$$ V = Q $$ \frac{1+\sqrt{2}}{2}\cdot1 & \frac{1-\sqrt{2}}{2}\cdot(-1) & 0\cdot1 \\
0\cdot1 & 0\cdot(-1) & 1\cdot1 \\
- **验证**： \tfrac12\cdot1 & \tfrac12\cdot(-1) & 0\cdot1
$$ U \Sigma V^\top = A $$ \end{bmatrix}
= \begin{bmatrix}
\dfrac{1+\sqrt{2}}{2} & \dfrac{\sqrt{2}-1}{2} & 0 \\
0 & 0 & 1 \\
\tfrac12 & -\tfrac12 & 0
\end{bmatrix}.
$$
5. 右奇异向量矩阵：
$$
V = Q.
$$
6. 验证
$$
A = U\,\Sigma\,V^\top
$$

16
科研/zy.md
View File

@ -8,18 +8,6 @@
实时重构出邻接矩阵a和权重矩阵 是否有帮助？ 带权邻接矩阵-》特征矩阵？ TGAT或EvolveGCN进行推理？
带权邻接矩阵仅作为边特征，特征矩阵？
社交网络中邻居关系，节点特征是不断变化的，可以利用TGAT或EvolveGCN进行预测，那么就要用已有训练集。但是不适合仿真使用，仿真是基于节点移动模型的。
关键假设：假设历史真实数据已知 可以拟合 二次函数 当作当前的测量值 因为我们要做实时估计 可能来不及获取实时值 但可以拟合过去的 关键假设：假设历史真实数据已知 可以拟合 二次函数 当作当前的测量值 因为我们要做实时估计 可能来不及获取实时值 但可以拟合过去的
或者直接谱分解上一个时刻重构的矩阵，得到特征值和特征向量序列 加上随机扰动作为观测输入 或者直接谱分解上一个时刻重构的矩阵，得到特征值和特征向量序列 加上随机扰动作为观测输入
@ -30,16 +18,12 @@
特征值误差分析（方差）直接看李振河的，滤波误差看郭款 特征值误差分析（方差）直接看李振河的，滤波误差看郭款
![image-20250624085529380](https://pic.bitday.top/i/2025/06/24/e57ix2-0.png) ![image-20250624085529380](https://pic.bitday.top/i/2025/06/24/e57ix2-0.png)

222
科研/小论文.md
View File

@ -4,9 +4,227 @@
2.卡尔曼滤波这边，Q、R不明确 / 真实若干时刻的测量值可以是真实值；但后面在线预测的时候仍然传的是真实值，事实上无法获取=》 考虑用三次指数平滑，对精确重构出来的矩阵谱分解，得到的特征值作为'真实值'，代入指数平滑算法中进行在线更新，执行单步计算。 2.卡尔曼滤波这边，Q、R不明确 / 真实若干时刻的测量值可以是真实值；但后面在线预测的时候仍然传的是真实值，事实上无法获取=》 考虑用三次指数平滑，对精确重构出来的矩阵谱分解，得到的特征值作为'真实值'，代入指数平滑算法中进行在线更新，执行单步计算。
3.所有特征值符号$\lambda$ 要改为奇异值 $σ$
4.这块有问题，没提高秩性，没说除了ER模型外的移动模型如RWP 4.这块有问题，没提高秩性，没说除了ER模型外的移动模型如RWP
![image-20250625093043478](https://pic.bitday.top/i/2025/06/25/fdxs6a-0.png) ![image-20250625093043478](https://pic.bitday.top/i/2025/06/25/fdxs6a-0.png)
## 指数平滑法
**指数平滑法（Single Exponential Smoothing）**
指数平滑法是一种对时间序列进行平滑和短期预测的简单方法。它假设近期的数据比更久之前的数据具有更大权重，并用一个平滑常数 $\alpha$（$0<\alpha\leq1$）来控制“记忆”长度。
- **平滑方程：**
$$
S_t = \alpha\,x_t + (1-\alpha)\,S_{t-1}
$$
- $x_t$：时刻 $t$ 的实际值
- $S_t$：时刻 $t$ 的平滑值（也可作为对 $x_{t+1}$ 的预测）
- $S_1$ 的初始值一般取 $x_1$
- **举例：**
假设一产品过去 5 期的销量为 $[100,\;105,\;102,\;108,\;110]$，取 $\alpha=0.3$，初始平滑值取 $S_1=x_1=100$：
1. $S_2=0.3\times105+0.7\times100=101.5$
2. $S_3=0.3\times102+0.7\times101.5=101.65$
3. $S_4=0.3\times108+0.7\times101.65\approx103.755$
4. $S_5=0.3\times110+0.7\times103.755\approx106.379$
因此，对第 6 期销量的预测就是 $S_5\approx106.38$。
**二次指数平滑法（Holt’s Linear Method）**
当序列存在趋势（Trend）时，单次平滑会落后。二次指数平滑（也称 Holt 线性方法）在单次平滑的基础上，额外对趋势项做平滑。
- **水平和趋势平滑方程：**
$$
\begin{cases}
L_t = \alpha\,x_t + (1-\alpha)(L_{t-1}+T_{t-1}), \\[6pt]
T_t = \beta\,(L_t - L_{t-1}) + (1-\beta)\,T_{t-1},
\end{cases}
$$
- $L_t$：水平（level）
- $T_t$：趋势（trend）
- $\alpha, \beta$：平滑常数，通常 $0.1$–$0.3$
- **预测公式：**
$$
\hat{x}_{t+m} = L_t + m\,T_t
$$
其中 $m$ 为预测步数。
- **举例：**
用同样的数据 $[100,105,102,108,110]$，取 $\alpha=0.3,\;\beta=0.2$，初始化：
- $L_1 = x_1 = 100$
- $T_1 = x_2 - x_1 = 5$
接下来计算：
1. $t=2$：
$$
L_2=0.3\times105+0.7\times(100+5)=0.3\times105+0.7\times105=105
$$
$$
T_2=0.2\times(105-100)+0.8\times5=0.2\times5+4=5
$$
2. $t=3$：
$$
L_3=0.3\times102+0.7\times(105+5)=0.3\times102+0.7\times110=106.4
$$
$$
T_3=0.2\times(106.4-105)+0.8\times5=0.2\times1.4+4=4.28
$$
3. $t=4$：
$$
L_4=0.3\times108+0.7\times(106.4+4.28)\approx0.3\times108+0.7\times110.68\approx110.276
$$
$$
T_4=0.2\times(110.276-106.4)+0.8\times4.28\approx0.2\times3.876+3.424\approx4.199
$$
4. $t=5$：
$$
L_5=0.3\times110+0.7\times(110.276+4.199)\approx0.3\times110+0.7\times114.475\approx112.133
$$
$$
T_5=0.2\times(112.133-110.276)+0.8\times4.199\approx0.2\times1.857+3.359\approx3.731
$$
**预测第 6 期** ($m=1$)：
$$
\hat{x}_6 = L_5 + 1\times T_5 \approx 112.133 + 3.731 = 115.864
$$
---
**小结**
- 单次指数平滑适用于无明显趋势的序列，简单易用。
- 二次指数平滑（Holt 方法）在水平外加趋势成分，适合带线性趋势的数据，并可向未来多步预测。
通过选择合适的平滑参数 $\alpha,\beta$ 并对初值进行合理设定，即可在实践中获得较好的短期预测效果。
**三次指数平滑法概述**
三次指数平滑法在二次（Holt）方法的基础上又加入了对季节成分的平滑，适用于同时存在趋势（Trend）和季节性（Seasonality）的时间序列。
**主要参数及符号**
- $m$：季节周期长度（例如季度数据 $m=4$，月度数据 $m=12$）。
- $\alpha, \beta, \gamma$：水平、趋势、季节三项的平滑系数，均在 $(0,1]$ 之间。
- $x_t$：时刻 $t$ 的实际值。
- $L_t$：时刻 $t$ 的水平（level）平滑值。
- $B_t$：时刻 $t$ 的趋势（trend）平滑值。
- $S_t$：时刻 $t$ 的季节（seasonal）成分平滑值。
- $\hat x_{t+h}$：时刻 $t+h$ 的 $h$ 步预测值。
**平滑与预测公式（加法模型）**
$$
\begin{aligned}
L_t &= \alpha\,(x_t - S_{t-m}) + (1-\alpha)\,(L_{t-1}+B_{t-1}),\\
B_t &= \beta\,(L_t - L_{t-1}) + (1-\beta)\,B_{t-1},\\
S_t &= \gamma\,(x_t - L_t) + (1-\gamma)\,S_{t-m},\\
\hat x_{t+h} &= L_t + h\,B_t + S_{t-m+h_m},\quad\text{其中 }h_m=((h-1)\bmod m)+1.
\end{aligned}
$$
- **加法模型** 适用于季节波动幅度与水平无关的情况；
- **乘法模型** 则把"$x_t - S_{t-m}$"改为"$x_t / S_{t-m}$"、"$S_t$"改为"$\gamma\,(x_t/L_t)+(1-\gamma)\,S_{t-m}$"并在预测中用乘法。
---
**计算示例**
假设我们有一个周期为 $m=4$ 的序列，前 8 期观测值：
$$
x = [110,\;130,\;150,\;95,\;120,\;140,\;160,\;100].
$$
取参数 $\alpha=0.5,\;\beta=0.3,\;\gamma=0.2$。
初始值按常见做法设定为：
- $L_0 = \frac{1}{m}\sum_{i=1}^m x_i = \tfrac{110+130+150+95}{4}=121.25$.
- 趋势初值
$$
B_0 = \frac{1}{m^2}\sum_{i=1}^m (x_{m+i}-x_i)
= \frac{(120-110)+(140-130)+(160-150)+(100-95)}{4\cdot4}
= \frac{35}{16} \approx 2.1875.
$$
- 季节初值 $S_i = x_i - L_0$，即
$[-11.25,\;8.75,\;28.75,\;-26.25]$ 对应 $i=1,2,3,4$。
下面我们演示第 5 期（$t=5$）的更新与对第 6 期的预测。
| $t$ | $x_t$ | 计算细节 | 结果 |
| -------------- | ----- | ---------------------------------------------------- | ----------------- |
| | | **已知初值** | |
| 0 | – | $L_0=121.25,\;B_0=2.1875$ | |
| 1–4 | – | $S_{1\ldots4}=[-11.25,\,8.75,\,28.75,\,-26.25]$ | |
| **5** | 120 | $L_5=0.5(120-(-11.25)) +0.5(121.25+2.1875)$ | $\approx127.3438$ |
| | | $B_5=0.3(127.3438-121.25)+0.7\cdot2.1875$ | $\approx3.3594$ |
| | | $S_5=0.2(120-127.3438)+0.8\cdot(-11.25)$ | $\approx-10.4688$ |
| **预测** $h=1$ | – | $\hat x_6 = L_5 + 1\cdot B_5 + S_{6-4}\;(=S_2=8.75)$ | $\approx139.45$ |
**解读：**
1. 期 5 时，剔除上周期季节影响后平滑得到新的水平 $L_5$；
2. 由水平变化量给出趋势 $B_5$；
3. 更新第 5 期的季节因子 $S_5$；
4. 期 6 的一步预测综合了最新水平、趋势和对应的季节因子，得 $\hat x_6\approx139.45$。
### 总结思考
- 如果你把预测值 $\hat x_{t+1}$ 当作"新观测"再去更新状态，然后再预测 $\hat x_{t+2}$，这种"预测—更新—预测"的迭代方式会让模型把自身的预测误差也当作输入，不断放大误差。
- 正确做法是——在时刻 $t$ 得到 $L_t,B_t,S_t$ 后，用上面的直接公式一次算出**所有未来** $\hat x_{t+1},\hat x_{t+2},\dots$，这样并不会"反馈"误差，也就没有累积放大的问题。
或者，根据精确重构出来的矩阵谱分解，得到的特征值作为'真实值'，进行在线更新，执行单步计算。

89
科研/草稿.md
View File

@ -1,57 +1,54 @@
Here's the reformatted version with Markdown + LaTeX, including explanations for the `*` symbol: **平滑（Smoothing）**
在时间序列分析中，“平滑”指的是用一种加权平均的方法，将原始序列中的随机波动（噪声）滤掉，突出其潜在的趋势和周期成分。指数平滑尤为典型：它对所有历史观测值 XtX_t 施加指数衰减的权重，使得离当前越近的数据权重越大、越远的数据权重越小，从而得到一条更为“平滑”的序列 StS_t。
--- - **单指数平滑（SES）**
**Input**: St=α Xt+(1−α) St−1,0<α<1 S_t = \alpha\,X_t + (1-\alpha)\,S_{t-1},\quad 0<\alpha<1
- Ordered singular value estimates
$$\tilde\sigma_1 \ge \tilde\sigma_2 \ge \cdots \ge \tilde\sigma_r,$$
- Budget
$$s \ge 0.$$
--- 其中，StS_t 是时刻 tt 的平滑值，α\alpha（平滑系数）控制新旧信息的权重比例。
### 1. Prefix Sum Array Initialization - **双指数平滑（Holt）**
$$S = [0] * (r+1)$$ 在 SES 的基础上，再引入一个“趋势分量” TtT_t：
> **Note**: The `*` symbol here is Python's list repetition operator, used to create a length $(r+1)$ array filled with zeros. In formal papers, this would typically be written as: {Lt=α Xt+(1−α)(Lt−1+Tt−1)Tt=β (Lt−Lt−1)+(1−β) Tt−1\begin{cases} L_t = \alpha\,X_t + (1-\alpha)(L_{t-1}+T_{t-1}) \\[6pt] T_t = \beta\,(L_t - L_{t-1}) + (1-\beta)\,T_{t-1} \end{cases}
> $$S_0 = S_1 = \cdots = S_r = 0$$
> or more concisely:
> $$S = \mathbf{0}_{r+1}.$$
### 2. Absolute Value Prefix Sum Computation 这里 LtL_t 是“平滑后的水平（level）”，TtT_t 是“平滑后的趋势（trend）”，β\beta 是趋势平滑系数。
For $\kappa=1,2,\dots,r$:
$$
S[\kappa] = S[\kappa-1] + \bigl|\tilde\sigma_\kappa\bigr|.
$$
### 3. Search Threshold Calculation - **三指数平滑（Holt–Winters）**
$$ 进一步加入季节性分量 StS_t：
\theta = S[r] - s.
$$
### 4. Binary Search on $S[0\ldots r]$ {Lt=α (Xt/St−m)+(1−α)(Lt−1+Tt−1)Tt=β (Lt−Lt−1)+(1−β) Tt−1St=γ (Xt/Lt)+(1−γ) St−m\begin{cases} L_t = \alpha\,(X_t/S_{t-m}) + (1-\alpha)(L_{t-1}+T_{t-1}) \\[4pt] T_t = \beta\,(L_t - L_{t-1}) + (1-\beta)\,T_{t-1} \\[4pt] S_t = \gamma\,(X_t/L_t) + (1-\gamma)\,S_{t-m} \end{cases}
Find the minimal $\kappa$ satisfying:
$$
S[\kappa] \ge \theta.
$$
**Pseudocode** (Python-style): 其中 mm 是季节周期长度，γ\gamma 是季节平滑系数。
```python
low, high = 0, r
while low < high:
mid = (low + high) // 2
if S[mid] < θ:
low = mid + 1
else:
high = mid
κ = low
```
--- ------
Key modifications: **预测逻辑**
1. Replaced all occurrences of $\tilde\lambda$ with $\tilde\sigma$ for consistency with SVD notation 指数平滑系列方法的核心假设是“未来的值可以用当前估计的水平、趋势、季节性分量线性组合”来近似。
2. Maintained proper LaTeX formatting with `$$` for display equations
3. Added clear section headers 1. **单指数平滑** 预测：
4. Preserved the Python-style pseudocode block
5. Included explanatory note about the `*` operator usage X^t+1=St \hat X_{t+1} = S_t
即，预测值等于最后一个时刻的平滑值。
2. **双指数平滑** 预测：
X^t+h=Lt+h Tt \hat X_{t+h} = L_t + h \, T_t
意味着：水平分量加上 hh 倍的趋势分量。
3. **三指数平滑** 预测：
X^t+h=(Lt+h Tt)×St+h−m⌊(h−1)/m⌋ \hat X_{t+h} = \bigl(L_t + h\,T_t\bigr)\times S_{t+h-m\lfloor (h-1)/m\rfloor}
即在双平滑的结果上，再乘以对应的季节系数。
整体来看，指数平滑的预测逻辑就是：
- **水平分量（Level）** 反映序列的基准水平；
- **趋势分量（Trend）** 反映序列的线性增长或下降趋势；
- **季节分量（Seasonality）** 反映序列的周期波动；
- 将它们按照简单的线性公式“拼装”起来，就得到对未来点的估计。
这种结构使得指数平滑既简单易算，又能灵活捕捉不同的时序特征。

25
论文/郭款论文.md
View File

@ -517,7 +517,7 @@ $$
#### 基于 SNMF 的网络嵌入 #### 基于 SNMF 的网络重构
文献[60]提出一种基于**简化特征分解**和**整体旋转**的近似方法(reduced Eigenvalue Decomposition，rEVD)： 文献[60]提出一种基于**简化特征分解**和**整体旋转**的近似方法(reduced Eigenvalue Decomposition，rEVD)：
@ -763,17 +763,22 @@ $$
**两种求对称非负矩阵分解的方法**
1. **纯梯度下降**
- 优点：实现原理简单，对任意大小/形状的矩阵都能做。
- 缺点：收敛速度有时较慢，且对初始值敏感。
2. **rEVD + 旋转截断** （示例方法）
- 优点：利用了特征分解，可以先一步把主要信息“压缩”进 $B$，后续只需解决“如何把负数修正掉”以及“如何微调逼近”。
- 缺点：需要先做特征分解，适合于对称矩阵或低秩场景。
### rSVD-旋转截断算法（$V_f/H_f$ 版）
| 步骤 | 公式 |
| -------------------- | ------------------------------------------------------------ |
| **1 输入** | 左奇异向量矩阵 $U_s \in \mathbb R^{n\times r}$<br>奇异值对角阵 $\Sigma \in \mathbb R^{r\times r}$ |
| **2 初始化** | $B = U_s\,\Sigma^{1/2}$<br>$Q = I_r$<br>$U = \max\!\bigl(0,B\bigr)$<br>设容差 $\varepsilon>0$ |
| **3 迭代：交替更新** | **3-a 更新 $U$** $U \leftarrow \max\bigl(0,\,B Q\bigr)$ <br>**3-b 更新 $Q$**<br>$\displaystyle F = U^{\mathsf T} B$<br>$\displaystyle F = V_f\,\Sigma_f\,H_f^{\mathsf T}$ ← SVD<br>$\displaystyle Q \leftarrow H_f\,V_f^{\mathsf T}$ |
| **4 停止条件** | 若 $\displaystyle \|\,U^{\mathsf T}(U - BQ)\|_F^{2} \le \varepsilon$ 则停止；否则回到 3 |
| **5 输出** | 重构矩阵 $\displaystyle A' = U\,U^{\mathsf T}$ |
$\kappa$
将原公式合并为一行，可写为：
$B \;\leftarrow\; U_s\,\Sigma^{1/2},\quad Q \;\leftarrow\; I_r,\quad U \;\leftarrow\;\max\bigl(0,\,B\bigr),\quad\varepsilon>0.$

191
论文/高飞论文.md
View File

@ -273,197 +273,6 @@ $$
## 指数平滑法
**指数平滑法（Single Exponential Smoothing）**
指数平滑法是一种对时间序列进行平滑和短期预测的简单方法。它假设近期的数据比更久之前的数据具有更大权重，并用一个平滑常数 $\alpha$（$0<\alpha\leq1$）来控制“记忆”长度。
- **平滑方程：**
$$
S_t = \alpha\,x_t + (1-\alpha)\,S_{t-1}
$$
- $x_t$：时刻 $t$ 的实际值
- $S_t$：时刻 $t$ 的平滑值（也可作为对 $x_{t+1}$ 的预测）
- $S_1$ 的初始值一般取 $x_1$
- **举例：**
假设一产品过去 5 期的销量为 $[100,\;105,\;102,\;108,\;110]$，取 $\alpha=0.3$，初始平滑值取 $S_1=x_1=100$：
1. $S_2=0.3\times105+0.7\times100=101.5$
2. $S_3=0.3\times102+0.7\times101.5=101.65$
3. $S_4=0.3\times108+0.7\times101.65\approx103.755$
4. $S_5=0.3\times110+0.7\times103.755\approx106.379$
因此，对第 6 期销量的预测就是 $S_5\approx106.38$。
**二次指数平滑法（Holt’s Linear Method）**
当序列存在趋势（Trend）时，单次平滑会落后。二次指数平滑（也称 Holt 线性方法）在单次平滑的基础上，额外对趋势项做平滑。
- **水平和趋势平滑方程：**
$$
\begin{cases}
L_t = \alpha\,x_t + (1-\alpha)(L_{t-1}+T_{t-1}), \\[6pt]
T_t = \beta\,(L_t - L_{t-1}) + (1-\beta)\,T_{t-1},
\end{cases}
$$
- $L_t$：水平（level）
- $T_t$：趋势（trend）
- $\alpha, \beta$：平滑常数，通常 $0.1$–$0.3$
- **预测公式：**
$$
\hat{x}_{t+m} = L_t + m\,T_t
$$
其中 $m$ 为预测步数。
- **举例：**
用同样的数据 $[100,105,102,108,110]$，取 $\alpha=0.3,\;\beta=0.2$，初始化：
- $L_1 = x_1 = 100$
- $T_1 = x_2 - x_1 = 5$
接下来计算：
1. $t=2$：
$$
L_2=0.3\times105+0.7\times(100+5)=0.3\times105+0.7\times105=105
$$
$$
T_2=0.2\times(105-100)+0.8\times5=0.2\times5+4=5
$$
2. $t=3$：
$$
L_3=0.3\times102+0.7\times(105+5)=0.3\times102+0.7\times110=106.4
$$
$$
T_3=0.2\times(106.4-105)+0.8\times5=0.2\times1.4+4=4.28
$$
3. $t=4$：
$$
L_4=0.3\times108+0.7\times(106.4+4.28)\approx0.3\times108+0.7\times110.68\approx110.276
$$
$$
T_4=0.2\times(110.276-106.4)+0.8\times4.28\approx0.2\times3.876+3.424\approx4.199
$$
4. $t=5$：
$$
L_5=0.3\times110+0.7\times(110.276+4.199)\approx0.3\times110+0.7\times114.475\approx112.133
$$
$$
T_5=0.2\times(112.133-110.276)+0.8\times4.199\approx0.2\times1.857+3.359\approx3.731
$$
**预测第 6 期** ($m=1$)：
$$
\hat{x}_6 = L_5 + 1\times T_5 \approx 112.133 + 3.731 = 115.864
$$
---
**小结**
- 单次指数平滑适用于无明显趋势的序列，简单易用。
- 二次指数平滑（Holt 方法）在水平外加趋势成分，适合带线性趋势的数据，并可向未来多步预测。
通过选择合适的平滑参数 $\alpha,\beta$ 并对初值进行合理设定，即可在实践中获得较好的短期预测效果。
**三次指数平滑法概述**
三次指数平滑法在二次（Holt）方法的基础上又加入了对季节成分的平滑，适用于同时存在趋势（Trend）和季节性（Seasonality）的时间序列。
**主要参数及符号**
- $m$：季节周期长度（例如季度数据 $m=4$，月度数据 $m=12$）。
- $\alpha, \beta, \gamma$：水平、趋势、季节三项的平滑系数，均在 $(0,1]$ 之间。
- $x_t$：时刻 $t$ 的实际值。
- $L_t$：时刻 $t$ 的水平（level）平滑值。
- $B_t$：时刻 $t$ 的趋势（trend）平滑值。
- $S_t$：时刻 $t$ 的季节（seasonal）成分平滑值。
- $\hat x_{t+h}$：时刻 $t+h$ 的 $h$ 步预测值。
**平滑与预测公式（加法模型）**
$$
\begin{aligned}
L_t &= \alpha\,(x_t - S_{t-m}) + (1-\alpha)\,(L_{t-1}+B_{t-1}),\\
B_t &= \beta\,(L_t - L_{t-1}) + (1-\beta)\,B_{t-1},\\
S_t &= \gamma\,(x_t - L_t) + (1-\gamma)\,S_{t-m},\\
\hat x_{t+h} &= L_t + h\,B_t + S_{t-m+h_m},\quad\text{其中 }h_m=((h-1)\bmod m)+1.
\end{aligned}
$$
- **加法模型** 适用于季节波动幅度与水平无关的情况；
- **乘法模型** 则把"$x_t - S_{t-m}$"改为"$x_t / S_{t-m}$"、"$S_t$"改为"$\gamma\,(x_t/L_t)+(1-\gamma)\,S_{t-m}$"并在预测中用乘法。
---
**计算示例**
假设我们有一个周期为 $m=4$ 的序列，前 8 期观测值：
$$
x = [110,\;130,\;150,\;95,\;120,\;140,\;160,\;100].
$$
取参数 $\alpha=0.5,\;\beta=0.3,\;\gamma=0.2$。
初始值按常见做法设定为：
- $L_0 = \frac{1}{m}\sum_{i=1}^m x_i = \tfrac{110+130+150+95}{4}=121.25$.
- 趋势初值
$$
B_0 = \frac{1}{m^2}\sum_{i=1}^m (x_{m+i}-x_i)
= \frac{(120-110)+(140-130)+(160-150)+(100-95)}{4\cdot4}
= \frac{35}{16} \approx 2.1875.
$$
- 季节初值 $S_i = x_i - L_0$，即
$[-11.25,\;8.75,\;28.75,\;-26.25]$ 对应 $i=1,2,3,4$。
下面我们演示第 5 期（$t=5$）的更新与对第 6 期的预测。
| $t$ | $x_t$ | 计算细节 | 结果 |
| -------------- | ----- | ---------------------------------------------------- | ----------------- |
| | | **已知初值** | |
| 0 | – | $L_0=121.25,\;B_0=2.1875$ | |
| 1–4 | – | $S_{1\ldots4}=[-11.25,\,8.75,\,28.75,\,-26.25]$ | |
| **5** | 120 | $L_5=0.5(120-(-11.25)) +0.5(121.25+2.1875)$ | $\approx127.3438$ |
| | | $B_5=0.3(127.3438-121.25)+0.7\cdot2.1875$ | $\approx3.3594$ |
| | | $S_5=0.2(120-127.3438)+0.8\cdot(-11.25)$ | $\approx-10.4688$ |
| **预测** $h=1$ | – | $\hat x_6 = L_5 + 1\cdot B_5 + S_{6-4}\;(=S_2=8.75)$ | $\approx139.45$ |
**解读：**
1. 期 5 时，剔除上周期季节影响后平滑得到新的水平 $L_5$；
2. 由水平变化量给出趋势 $B_5$；
3. 更新第 5 期的季节因子 $S_5$；
4. 期 6 的一步预测综合了最新水平、趋势和对应的季节因子，得 $\hat x_6\approx139.45$。
### 总结思考
- 如果你把预测值 $\hat x_{t+1}$ 当作"新观测"再去更新状态，然后再预测 $\hat x_{t+2}$，这种"预测—更新—预测"的迭代方式会让模型把自身的预测误差也当作输入，不断放大误差。
- 正确做法是——在时刻 $t$ 得到 $L_t,B_t,S_t$ 后，用上面的直接公式一次算出**所有未来** $\hat x_{t+1},\hat x_{t+2},\dots$，这样并不会"反馈"误差，也就没有累积放大的问题。
或者，根据精确重构出来的矩阵谱分解，得到的特征值作为'真实值'，进行在线更新，执行单步计算。
## 特征值精度预估 ## 特征值精度预估
### 1. 噪声随机变量与协方差 ### 1. 噪声随机变量与协方差

160
项目/拼团交易系统.md
View File

@ -940,7 +940,7 @@ public Object postProcessAfterInitialization(Object bean, String name) {
### HTTP客戶端框架 ### OkHttpClient
**引入依赖** **引入依赖**
@ -1020,3 +1020,161 @@ public Object postProcessAfterInitialization(Object bean, String name) {
- 避免在代码各处手动 `new OkHttpClient()`、重复配置。 - 避免在代码各处手动 `new OkHttpClient()`、重复配置。
### Retrofit
微信登录时，需要调用微信提供的接口做验证。
#### 快速入门
// 1. 定义 DTO
```java
public class User {
private String id;
private String name;
// … 省略 getters/setters …
}
```
// 2. 定义 Retrofit 接口
```java
public interface ApiService {
@GET("users/{id}")
Call<User> getUser(@Path("id") String id);
}
```
// 3. 配置 Retrofit 并注册为 Spring Bean
```java
@Configuration
public class RetrofitConfig {
private static final String BASE_URL = "https://api.example.com/";
@Bean
public Retrofit retrofit() {
return new Retrofit.Builder()
.baseUrl(BASE_URL) // 公共前缀
.addConverterFactory(JacksonConverterFactory.create()) // 自动 JSON ↔ DTO
.build();
}
@Bean
public ApiService apiService(Retrofit retrofit) {
// 动态生成 ApiService 实现
return retrofit.create(ApiService.class);
}
}
```
// 4. 在业务层注入并调用
```java
@Service
public class UserService {
private final ApiService apiService;
public UserService(ApiService apiService) {
this.apiService = apiService;
}
/**
* 同步方式获取用户信息
*/
public User getUserById(String userId) {
try {
Call<User> call = apiService.getUser(userId);
Response<User> resp = call.execute();
if (resp.isSuccessful()) {
return resp.body();
} else {
// 根据业务需要抛出异常或返回 null
throw new RuntimeException("请求失败，HTTP " + resp.code());
}
} catch (Exception e) {
throw new RuntimeException("调用用户服务出错", e);
}
}
/**
* 异步方式获取用户信息
*/
public void getUserAsync(String userId) {
apiService.getUser(userId).enqueue(new retrofit2.Callback<User>() {
@Override
public void onResponse(Call<User> call, Response<User> response) {
if (response.isSuccessful()) {
User user = response.body();
// TODO: 处理 user
}
}
@Override
public void onFailure(Call<User> call, Throwable t) {
// TODO: 处理异常
}
});
}
}
```
Retrofit 在运行时会生成这个接口的实现类，帮你完成：
- 拼 URL（把 `{id}` 换成具体值）
- 发起 GET 请求
- 拿到响应的 JSON 并自动反序列化成 `User` 对象
| 核心点 | Apache HttpClient | Retrofit |
| --------------- | ----------------------------------------- | ------------------------------------------------------------ |
| 编程模型 | 细粒度调用，手动构造 `HttpGet`/`HttpPost` | 注解驱动接口方法，声明式调用 |
| 请求定义 | 手动拼接 URL、参数 | 用 `@GET`/`@POST`、`@Path`、`@Query`、`@Body` 注解 |
| 序列化/反序列化 | 手动调用 `ObjectMapper`/`Gson` | 自动通过 `ConverterFactory`（Jackson/Gson 等） |
| 同步/异步 | 以同步为主，异步需自行管理线程和回调 | 同一个 `Call<T>` 即可 `execute()`（同步）或 `enqueue()`（异步） |
| 扩展性与拦截器 | 可配置拦截器，但需手动集成 | 底层基于 OkHttp，天然支持拦截器、连接池、缓存、重试和取消 |
### 微信扫码登录流程
![image-20250711192110034](https://pic.bitday.top/i/2025/07/11/vrgj6u-0.png)
**1.前端请求二维码凭证**
- 用户点击“扫码登录”，前端向后端发 `GET /api/v1/login/weixin_qrcode_ticket`。
- 后端获取 access_token
1.先尝试从本地缓存（如 Guava Cache）读取 `access_token`；
2.若无或已过期，则请求微信接口：
```ruby
GET https://api.weixin.qq.com/cgi-bin/token
?grant_type=client_credential
&appid={你的 AppID}
&secret={你的 AppSecret}
```
微信返回 `{ "access_token":"ACCESS_TOKEN_VALUE", "expires_in":7200 }`，后端缓存这个值（有效期约 2 小时）。
- 后端利用 `access_token` 创建二维码 ticket，返给前端。
**2.前端展示二维码**
- 前端根据 `ticket` 生成二维码链接：`https://mp.weixin.qq.com/cgi-bin/showqrcode?ticket={ticket}`
**3.微信回调后端**
- 用户确认扫描后，微信服务器向你预先配置的**回调 URL**（如 `POST /api/v1/weixin/portal/receive`）推送包含 `ticket` 和 `openid` 的消息。
- 后端：将 `ticket → openid` **存入缓存**（`openidToken.put(ticket, openid)`）；调用 `sendLoginTemplate(openid)` 给用户推送“登录成功”模板消息（手机公众号上推送，非网页）
**4.前端获知登录结果**
- **轮询方式**：生成二维码后，前端每隔几秒向后端发送 `ticket`来验证登录状态，后端**查缓存**来判断 `ticket` 对应用户是否成功登录。
- **推送方式**：前端通过 WebSocket/SSE 建立长连接，后端回调处理完成后直接往该连接推送登录成功及 JWT。

10
项目/智能协同云图库.md
View File

@ -157,6 +157,16 @@ private static final long serialVersionUID = -1321880859645675653L;
### 胡图工具类hutool ### 胡图工具类hutool
**引入依赖**
```xml
<dependency>
<groupId>cn.hutool</groupId>
<artifactId>hutool-all</artifactId>
<version>5.8.26</version>
</dependency>
```
`ObjUtil.isNotNull(Object obj)`，仅判断对象是否 **不为 `null`**，不关心对象内容是否为空，比如空字符串 `""`、空集合 `[]`、数字 `0` 等都算是“非 null”。 `ObjUtil.isNotNull(Object obj)`，仅判断对象是否 **不为 `null`**，不关心对象内容是否为空，比如空字符串 `""`、空集合 `[]`、数字 `0` 等都算是“非 null”。
`ObjUtil.isNotEmpty(Object obj)` 判断对象是否 **不为 null 且非“空”** `ObjUtil.isNotEmpty(Object obj)` 判断对象是否 **不为 null 且非“空”**

86
项目/苍穹外卖.md
View File

@ -376,6 +376,12 @@ APIFox 能够导入包括 YApi 格式在内的多种接口文档，同时支持
**与Idea集成**
安装plugin Apifox-helper，配置token，即可直接在controller层接口右键 "upload to Apifox"
#### Swagger #### Swagger
1. 使得前后端分离开发更加方便，有利于团队协作 1. 使得前后端分离开发更加方便，有利于团队协作
@ -525,11 +531,15 @@ public class EmployeeController {
</dependency> </dependency>
``` ```
**打包方式：** **打包方式（本地）：**
法一.直接对父工程执行mvn clean install
法二.分别先对子模块common和pojo执行install，再对server执行package
注意：直接对server打包会报错！！！
1.直接对父工程执行mvn clean install
2.分别对子模块common和pojo执行install，再对server执行package
因为Maven 在构建 `sky-server` 时，去你本地仓库或远程仓库寻找它依赖的两个 SNAPSHOT 包。 因为Maven 在构建 `sky-server` 时，去你本地仓库或远程仓库寻找它依赖的两个 SNAPSHOT 包。
@ -719,7 +729,40 @@ ENTRYPOINT ["java", "-jar", "app.jar"]
``` ```
2.maven构建依赖可能比较慢，需创建.mvn/settings.xml
**命令解析：**
```dockerfile
mvn dependency:go-offline -B 这一步只做依赖预取，也就是把所有在父 POM、子模块 POM、以及插件里声明的第三方库都下载到本地仓库（~/.m2/repository）
```
```dockerfile
真正的编译+构建打包步骤：
RUN mvn -f whut-take-out-backend/pom.xml clean package \
-pl sky-server -am \
-DskipTests -B
-f whut-take-out-backend/pom.xml 指定使用哪个 POM 作为构建入口（父工程）。
clean: 把上一次构建残留的 target/ 目录删掉，保证从零开始构建
package：执行到 package 阶段 生成 JAR/WAR
-pl sky-server (--projects) 只针对 sky-server 模块执行后续构建。
-am (--also-make) 如果 sky-server 依赖了多模块工程里的其他子模块（如 common、pojo），就会先把它们编译好，确保 sky-server 拿到最新的本地模块依赖。
-DskipTests
跳过单元测试，加快构建速度。
-B
批处理模式（无交互），适合 Docker 构建。
```
2.maven构建依赖可能比较慢，需创建.mvn/settings.xml （这个提速非常多！务必添加）
```xml ```xml
<settings xmlns="http://maven.apache.org/SETTINGS/1.1.0" <settings xmlns="http://maven.apache.org/SETTINGS/1.1.0"
@ -743,6 +786,29 @@ ENTRYPOINT ["java", "-jar", "app.jar"]
### 踩坑总结
Maven 默认会用 `artifactId-version`来命名,eg：
```xml
<artifactId>group-buying-sys</artifactId>
<version>1.0-SNAPSHOT</version>
```
`group-buying-sys-app-1.0-SNAPSHOT.jar`
如果server模块中的pom中指定了finalName，那么打包出来的文件将命名为finalName中指定的名称，如 `example-app.jar`
```xml
<build>
<finalName>example-app</finalName>
</build>
```
这个问题导致docker-compose构建镜像时一直报错：`Error: Unable to access jarfile app.jar`
## 前端部署 ## 前端部署
直接部署开发完毕的前端代码，准备： 直接部署开发完毕的前端代码，准备：
@ -1582,7 +1648,7 @@ Mapper 执行动态 SQL，将已填充的字段写入数据库
- 创建Http请求对象 - 创建Http请求对象
- 调用HttpClient的execute方法发送请求 - 调用HttpClient的execute方法发送请求
**测试用例** ### 快速入门
```java ```java
@SpringBootTest @SpringBootTest
@ -1651,6 +1717,10 @@ public class HttpClientTest {
} }
``` ```
使用时将`GET POST`方法单独封装到`HttpClient`工具类中，Service层中直接使用工具类，传入需要的请求体即可。
## 微信小程序 ## 微信小程序
@ -1662,11 +1732,11 @@ public class HttpClientTest {
1. 小程序端，调用wx.login()获取code，就是授权码。 1. 小程序端，调用wx.login()获取code，就是授权码。
2. 小程序端，调用wx.request()发送请求并携带code，请求开发者服务器(自己编写的后端服务)。 2. 小程序端，调用wx.request()发送请求并携带code，请求开发者服务器(自己编写的后端服务)。
3. 开发者服务端，通过HttpClient向微信接口服务发送请求，并携带appId+appsecret+code三个参数。 3. 开发者服务端，通过HttpClient向微信接口服务发送请求，并携带appId+appsecret+code三个参数。
4. 开发者服务端，接收微信接口服务返回的数据，session_key+opendId等。opendId是微信用户的唯一标识。 4. 开发者服务端，接收微信接口服务返回的数据，session_key+opendId等。**opendId是微信用户的唯一标识**。
5. 开发者服务端，自定义登录态，生成令牌(token)和openid等数据返回给小程序端，方便后绪请求身份校验。 5. 开发者服务端，自定义登录态，生成令牌token和openid等数据返回给小程序端，方便后绪请求身份校验。
6. 小程序端，收到自定义登录态，存储storage。 6. 小程序端，收到自定义登录态，存储storage。
7. 小程序端，后绪通过wx.request()发起业务请求时，携带token。 7. 小程序端，后绪通过wx.request()发起业务请求时，携带token。
8. 开发者服务端，收到请求后，通过携带的token，解析当前登录用户的id（无需获取openai，因为token中存了userid可以确认用户身份）。 8. 开发者服务端，收到请求后，通过携带的token，解析当前登录用户的id（无需获取openid，因为token中存了userid可以确认用户身份）。
9. 开发者服务端，身份校验通过后，继续相关的业务逻辑处理，最终返回业务数据。 9. 开发者服务端，身份校验通过后，继续相关的业务逻辑处理，最终返回业务数据。

9
项目/草稿.md Normal file
View File

@ -0,0 +1,9 @@
核心比较如下：
| 核心点 | Apache HttpClient | Retrofit |
| --------------- | ----------------------------------------- | ------------------------------------------------------------ |
| 编程模型 | 细粒度调用，手动构造 `HttpGet`/`HttpPost` | 注解驱动接口方法，声明式调用 |
| 请求定义 | 手动拼接 URL、参数 | 用 `@GET`/`@POST`、`@Path`、`@Query`、`@Body` 注解 |
| 序列化/反序列化 | 手动调用 `ObjectMapper`/`Gson` | 自动通过 `ConverterFactory`（Jackson/Gson 等） |
| 同步/异步 | 以同步为主，异步需自行管理线程和回调 | 同一个 `Call<T>` 即可 `execute()`（同步）或 `enqueue()`（异步） |
| 扩展性与拦截器 | 可配置拦截器，但需手动集成 | 底层基于 OkHttp，天然支持拦截器、连接池、缓存、重试和取消 |