Commit on 2025/03/29 周六 11:33:34.72
This commit is contained in:
parent
34e53e1a72
commit
75d8cb67a1
167
科研/KAN.md
Normal file
167
科研/KAN.md
Normal file
@ -0,0 +1,167 @@
|
||||
## KAN
|
||||
|
||||
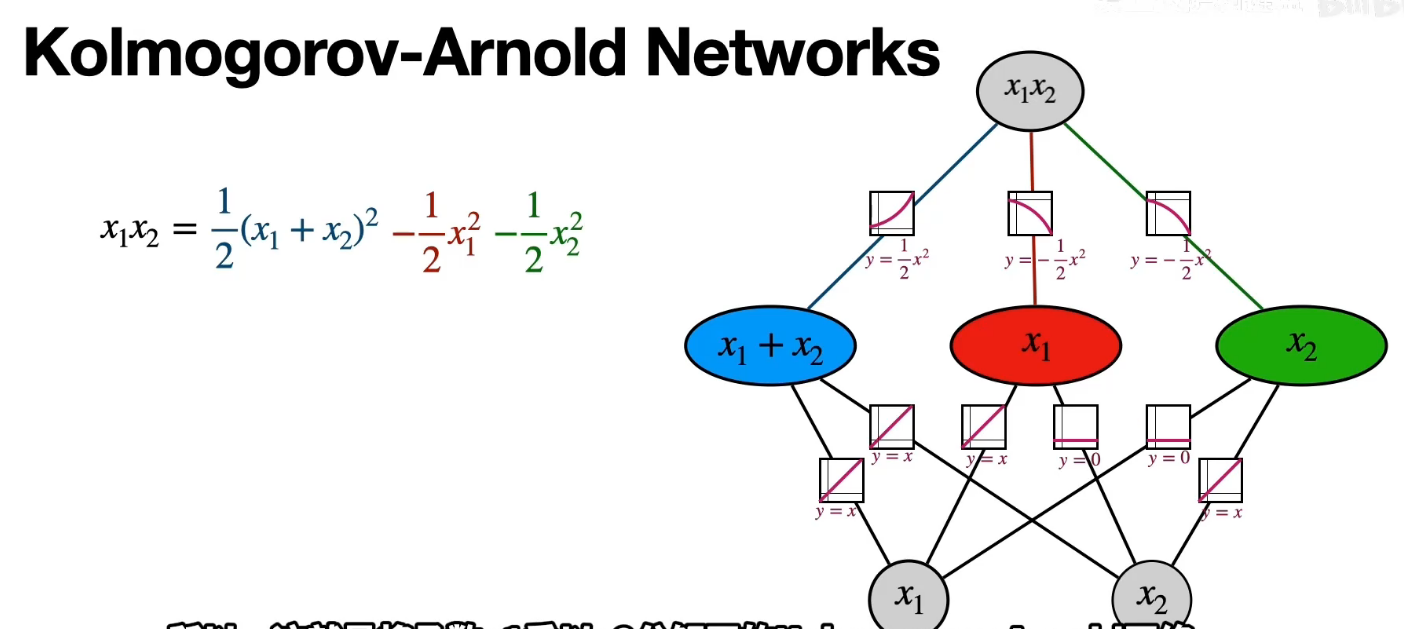
### Kolmogorov-Arnold表示定理
|
||||
|
||||
该定理表明,任何多元连续函数都可以表示为有限个单变量函数的组合。
|
||||
|
||||
对于任意一个定义在$[0,1]^n$上的**连续多元函数**:
|
||||
$$ f(x_1, x_2, \ldots, x_n), $$
|
||||
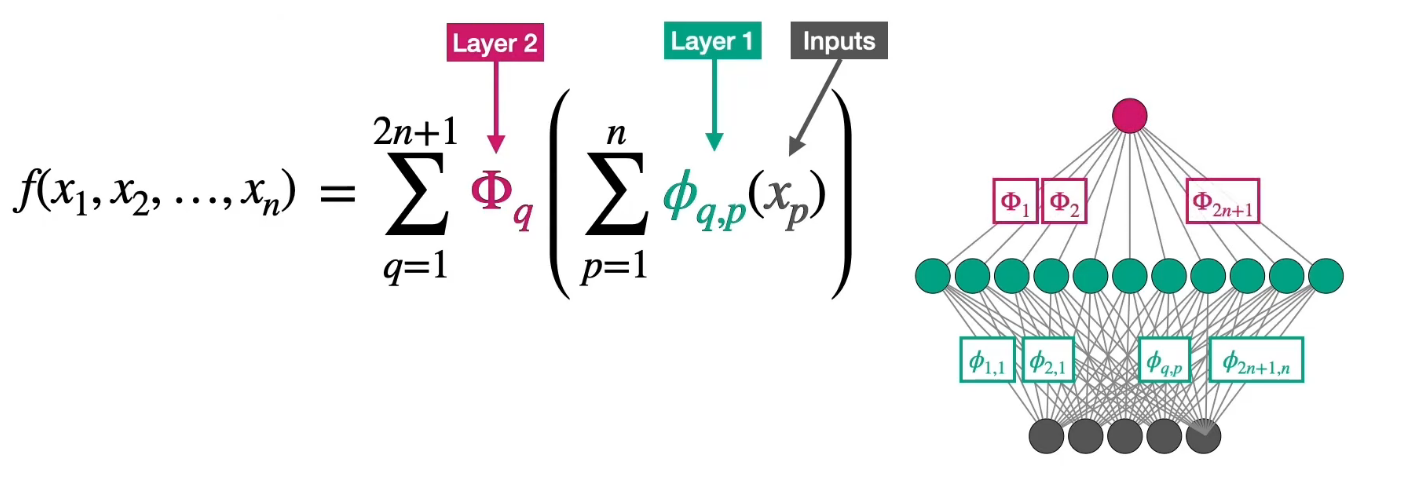
存在**单变量连续函数** $\phi_{q}$ 和 $\psi_{q,p}$(其中 $q = 1, 2, \ldots, 2n+1$,$p = 1, 2, \ldots, n$),使得:
|
||||
$$
|
||||
f(x_1, \ldots, x_n) = \sum_{q=1}^{2n+1} \phi_{q}\left( \sum_{p=1}^{n} \psi_{q,p}(x_p) \right).
|
||||
$$
|
||||
即,$f$可以表示为$2n+1$个“外层函数”$\phi_{q}$和$n \times (2n+1)$个“内层函数”$\psi_{q,p}$的组合。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
#### **和MLP的联系**
|
||||
|
||||
| **Kolmogorov-Arnold定理** | **神经网络(MLP)** |
|
||||
| -------------------------------- | ---------------------------------------------------- |
|
||||
| 外层函数 $\phi_q$ 的叠加 | 输出层的加权求和(线性组合) + 激活函数 |
|
||||
| 内层函数 $\psi_{q,p}$ 的线性组合 | 隐藏层的加权求和 + 非线性激活函数 |
|
||||
| 固定 $2n+1$ 个“隐藏单元” | 隐藏层神经元数量可以自由设计,依赖于网络的深度和宽度 |
|
||||
| 严格的数学构造(存在性证明) | 通过数据驱动的学习(基于梯度下降等方法)来优化参数 |
|
||||
|
||||
#### **和MLP的差异**
|
||||
|
||||
浅层结构(一个隐藏层)的数学表达与模型设计
|
||||
|
||||
| **模型** | **数学公式** | **模型设计** |
|
||||
| -------- | ------------------------------------------------------------ | ---------------------------------------------------------- |
|
||||
| **MLP** | $f(x) \approx \sum_{i=1}^{N} a_i \sigma(w_i \cdot x + b_i)$ | 线性变换后再跟非线性激活函数(RELU) |
|
||||
| **KAN** | $f(x) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right)$ | **可学习激活函数**(如样条)在边上,**求和操作**在神经元上 |
|
||||
|
||||
边上的可学习函数: $\phi_{q,p}(x_p)$(如B样条)
|
||||
|
||||
求和操作:$\sum_{p=1}^n \phi_{q,p}(x_p)$
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
深层结构的数学表达与模型设计
|
||||
|
||||
| **模型** | **数学公式** | **模型设计** |
|
||||
| -------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
|
||||
| **MLP** | $\text{MLP}(x) = (W_3 \circ \sigma_2 \circ W_2 \circ \sigma_1 \circ W_1)(x)$ | 交替的线性层($W_i$)和固定非线性激活函数($\sigma_i$)。 |
|
||||
| **KAN** | $\text{KAN}(x) = (\Phi_3 \circ \Phi_2 \circ \Phi_1)(x)$ | 每一层都是单变量函数的组合($\Phi_i$),每一层的激活函数都可以进行学习 |
|
||||
|
||||
|
||||
|
||||
### 传统MLP的缺陷
|
||||
|
||||
1. **梯度消失和梯度爆炸**:
|
||||
与其他传统的激活函数(如 Sigmoid 或 Tanh)一样,MLP 在进行反向传播时有时就会遇到梯度消失/爆炸的问题,尤其当网络层数过深时。当它非常小或为负大,网络会退化;连续乘积会使得梯度慢慢变为 0(梯度消失)或变得异常大(梯度爆炸),从而阻碍学习过程。
|
||||
2. **参数效率**:
|
||||
MLP 常使用全连接层,每层的每个神经元都与上一层的所有神经元相连。尤其是对于大规模输入来说,这不仅增加了计算和存储开销,也增加了过拟合的风险。效率不高也不够灵活。
|
||||
3. **处理高维数据能力有限**:MLP 没有利用数据的内在结构(例如图像中的局部空间相关性或文本数据的语义信息)。例如,在图像处理中,MLP 无法有效地利用像素之间的局部空间联系,这很典型在图像识别等任务上的性能不如卷积神经网络(CNN)。
|
||||
4. **长依赖问题**:
|
||||
虽然 MLP 理论上可以逼近任何函数,但在实际应用中,它们很难捕捉到序列中的长依赖关系(例如句子跨度很长)。这让人困惑:如何把前后序列的信息互相处理?而自注意力(如 transformer)在这类任务中表现更好。
|
||||
|
||||
但无论CNN/RNN/transformer怎么改进,都躲不掉MLP这个基础模型根上的硬伤,即线性组合+激活函数的模式。
|
||||
|
||||
|
||||
|
||||
### KAN网络
|
||||
|
||||
#### **主要贡献:**
|
||||
|
||||
过去的类似想法受限于原始的Kolmogorov-Arnold表示定理(两层网络,宽度为2n+12*n*+1),未能利用现代技术(如反向传播)进行训练。
|
||||
|
||||
KAN通过推广到**任意宽度和深度**的架构,解决了这一限制,同时通过实验验证了KAN在“AI + 科学”任务中的有效性,兼具**高精度**和**可解释性**。
|
||||
|
||||
|
||||
|
||||
#### **B样条(B-spline)**
|
||||
|
||||
是一种通过分段多项式函数的线性组合构造的光滑曲线,其核心思想是利用**局部基函数**(称为B样条基函数)来表示整个曲线。
|
||||
|
||||
形式上,一个B样条函数通常表示为基函数的线性组合:
|
||||
|
||||
$$
|
||||
S(t) = \sum_{i=0}^{n} c_i \cdot B_i(t)
|
||||
$$
|
||||
|
||||
其中:
|
||||
|
||||
- $B_i(t)$ 是 **B样条基函数**(basis functions);
|
||||
- $c_i$ 是 **控制点** 或系数(可以来自数据、拟合、插值等);
|
||||
- $S(t)$ 是最终的 **B样条曲线** 或函数。
|
||||
|
||||
每个基函数只在某个局部区间内非零,改变一个控制点只会影响曲线的局部形状。
|
||||
|
||||
**示例:基函数定义**
|
||||
|
||||
$B_0(t)$ - 支撑区间[0,1]
|
||||
$$
|
||||
B_0(t) =
|
||||
\begin{cases}
|
||||
1 - t, & 0 \leq t < 1,\\
|
||||
0, & \text{其他区间}.
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$B_1(t)$ - 支撑区间[0,2]
|
||||
$$
|
||||
B_1(t) =
|
||||
\begin{cases}
|
||||
t, & 0 \leq t < 1, \\
|
||||
2 - t, & 1 \leq t < 2, \\
|
||||
0, & \text{其他区间}.
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$B_2(t)$ - 支撑区间[1,3]
|
||||
$$
|
||||
B_2(t) =
|
||||
\begin{cases}
|
||||
t - 1, & 1 \leq t < 2, \\
|
||||
3 - t, & 2 \leq t < 3, \\
|
||||
0, & \text{其他区间}.
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$B_3(t)$ - 支撑区间[2,4]
|
||||
$$
|
||||
B_3(t) =
|
||||
\begin{cases}
|
||||
t - 2, & 2 \leq t < 3, \\
|
||||
4 - t, & 3 \leq t \leq 4, \\
|
||||
0, & \text{其他区间}.
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/03/27/ngzlqp-0.png" alt="image-20250327141925257" style="zoom:80%;" />
|
||||
|
||||
假设用该基函数对$f(t) = \sin\left(\dfrac{\pi t}{4}\right)$在[0,4]区间上拟合
|
||||
$$
|
||||
S(t) = 0 \cdot B_0(t) + 0.7071 \cdot B_1(t) + 1 \cdot B_2(t) + 0.7071 \cdot B_3(t)
|
||||
$$
|
||||
<img src="https://pic.bitday.top/i/2025/03/27/npyud0-0.png" alt="image-20250327143432551" style="zoom: 80%;" />
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
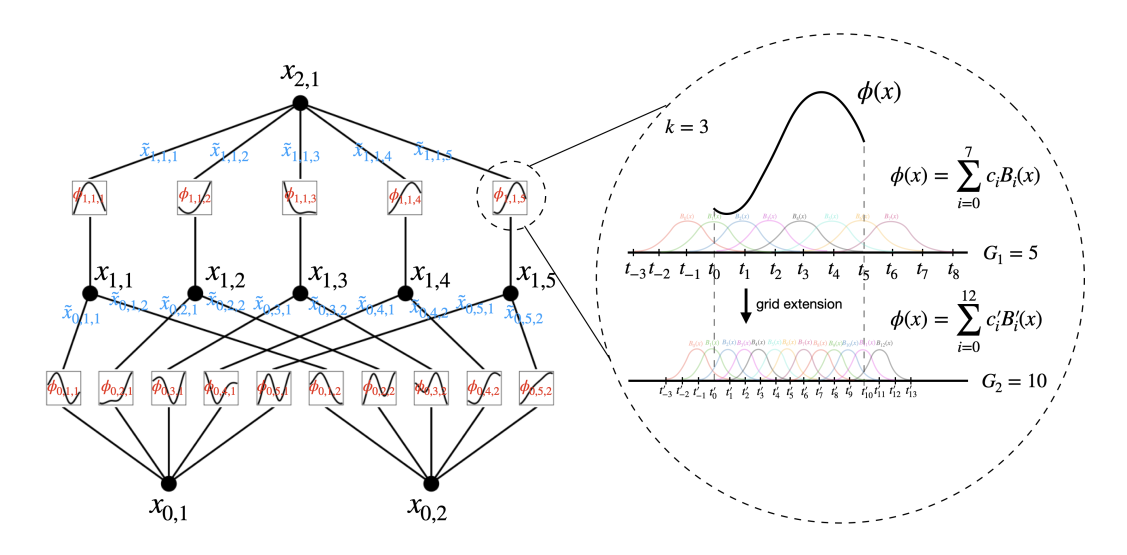
#### **网络结构:**
|
||||
|
||||
|
||||
|
||||
左图:
|
||||
|
||||
- 节点(如$x_{l,i}$)表示第$l$层第$i$个神经元的**输入值**
|
||||
- 边(如$\phi_{l,j,i}$)表示**可学习的激活函数**(权重)
|
||||
- 下一层节点的值计算:
|
||||
$$x_{l+1,j} = \sum_i \phi_{l,j,i}(x_{l,i})$$
|
||||
|
||||
右图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
26
科研/图神经网络.md
26
科研/图神经网络.md
@ -1,3 +1,5 @@
|
||||
李振河 陈茂森
|
||||
|
||||
# 图神经网络
|
||||
|
||||
图表示学习的本质是把节点映射成低维连续稠密的向量。这些向量通常被称为 **嵌入(Embedding)**,它们能够捕捉节点在图中的结构信息和属性信息,从而用于下游任务(如节点分类、链接预测、图分类等)。
|
||||
@ -16,11 +18,11 @@
|
||||
|
||||
这种做法面临重大问题,导致其**并不可行**:
|
||||
|
||||
1. **$O(|V|^2)$ 参数量** ,参数量庞大
|
||||
1. $O(|V|^2)$ 参数量 ,参数量庞大
|
||||
|
||||
2. **无法适应不同大小的图** ,需要固定输入维度
|
||||
2. 无法适应不同大小的图 ,需要固定输入维度
|
||||
|
||||
3. **对节点顺序敏感** ,节点编号顺序一变,输入就完全变样,但其实图的拓扑并没变(仅节点编号/排列方式不同)。
|
||||
3. 对节点顺序敏感 ,节点编号顺序一变,输入就完全变样,但其实图的拓扑并没变(仅节点编号/排列方式不同)。
|
||||
|
||||
```text
|
||||
A —— B
|
||||
@ -57,11 +59,11 @@
|
||||
|
||||
在**图神经网络**里,通常每个节点$v$ 都有一个**局部计算图**,用来表示该节点在聚合信息时所需的所有邻居(及邻居的邻居……)的依赖关系。
|
||||
|
||||
- 直观理解
|
||||
- 以节点 $v$ 为根;
|
||||
- 1-hop 邻居在第一层,2-hop 邻居在第二层……
|
||||
- 逐层展开直到一定深度(例如 k 层)。
|
||||
- 这样形成一棵“邻域树”或“展开图”,其中每个节点都需要从其子节点(邻居)获取特征进行聚合。
|
||||
直观理解
|
||||
- 以节点 $v$ 为根;
|
||||
- 1-hop 邻居在第一层,2-hop 邻居在第二层……
|
||||
- 逐层展开直到一定深度(例如 k 层)。
|
||||
- 这样形成一棵“邻域树”或“展开图”,其中每个节点都需要从其子节点(邻居)获取特征进行聚合。
|
||||
|
||||
|
||||
|
||||
@ -211,7 +213,7 @@ $$
|
||||
|
||||
## GCN
|
||||
|
||||
在 GNN 里,归一化(normalization)的核心目的就是 **平衡不同节点在信息传播(message‑passing)中的影响力**,避免「高连通度节点(high‑degree nodes)」主导了所有邻居的特征聚合。
|
||||
在 GCN 里,归一化(normalization)的核心目的就是 **平衡不同节点在信息传播(message‑passing)中的影响力**,避免「高连通度节点(high‑degree nodes)」主导了所有邻居的特征聚合。
|
||||
|
||||
$H' = \tilde D^{-1}\,\tilde A\,\tilde D^{-1}H$
|
||||
|
||||
@ -253,7 +255,7 @@ $$
|
||||
|
||||
|
||||
|
||||
**优化**
|
||||
**GraphSAGE优化**
|
||||
$$
|
||||
h_v^{(k+1)} = \sigma \Big(
|
||||
\mathbf{W}_{\text{self}}^{(k)} \cdot h_v^{(k)}
|
||||
@ -321,7 +323,7 @@ $$
|
||||
\mathbf{a} = \begin{bmatrix}1 \\ 1 \\ 1 \\ 1\end{bmatrix}.
|
||||
$$
|
||||
|
||||
- 激活函数使用 LeakyReLU(负斜率设为0.2,但本例中结果为正数,所以不变)。
|
||||
- 激活函数使用 LeakyReLU(负数斜率设为0.2,但本例中结果为正数,所以不变)。
|
||||
|
||||
---
|
||||
|
||||
@ -382,6 +384,8 @@ $$
|
||||
|
||||
**多头注意力(隐藏层时拼接)**
|
||||
|
||||
每个头都有自己的一组可学习参数,并独立计算注意力系数和输出特征。以捕捉邻居节点的多种不同关系或特征。
|
||||
|
||||
如果有 $K$ 个独立的注意力头,每个头输出 $\mathbf{h}_i'^{(k)}$,则拼接后的输出为:
|
||||
$$
|
||||
\mathbf{h}_i' =
|
||||
|
||||
260
科研/草稿.md
260
科研/草稿.md
@ -1,233 +1,41 @@
|
||||
---
|
||||
# B样条拟合示例:用正弦函数采样作为系数
|
||||
|
||||
## 该部分主要内容概述
|
||||
我选择的系数是通过在四个节点处对函数 $f(t) = \sin\left(\dfrac{\pi t}{4}\right)$ 进行采样得到的,对应的是四个基函数 $B_0(t), B_1(t), B_2(t), B_3(t)$,其"峰值"分别位于:
|
||||
|
||||
在这部分(论文 2.1 节 “Graph Attentional Layer”)中,作者提出了图注意力网络(GAT)中最核心的运算:**图注意力层**。它的基本思想是:
|
||||
- $B_0(t)$:在 $t = 0$ 处取值 1
|
||||
- $B_1(t)$:在 $t = 1$ 处取值 1
|
||||
- $B_2(t)$:在 $t = 2$ 处取值 1
|
||||
- $B_3(t)$:在 $t = 3$ 处取值 1
|
||||
|
||||
1. **线性变换**:先对每个节点的特征 $\mathbf{h}_i$ 乘上一个可学习的权重矩阵 $W$,得到变换后的特征 $W \mathbf{h}_i$。
|
||||
2. **自注意力机制**:通过一个可学习的函数 $a$,对节点 $i$ 和其邻居节点 $j$ 的特征进行计算,得到注意力系数 $e_{ij}$。这里会对邻居进行遮蔽(masked attention),即只计算图中有边连接的节点对。
|
||||
3. **归一化**:将注意力系数 $e_{ij}$ 通过 softmax 进行归一化,得到 $\alpha_{ij}$,表示节点 $j$ 对节点 $i$ 的重要性权重。
|
||||
4. **聚合**:最后利用注意力系数加权邻居节点的特征向量,并经过激活函数得到新的节点表示 $\mathbf{h}_i'$。
|
||||
5. **多头注意力**:为增强表示能力,可并行地执行多个独立的注意力头(multi-head attention),再将它们的结果进行拼接(或在最后一层进行平均),从而得到最终的节点表示。
|
||||
## 系数计算过程
|
||||
|
||||
该部分给出的公式主要包括注意力系数的计算、softmax 归一化、多头注意力的聚合方式等,下面逐一用 Markdown 数学公式的形式列出。
|
||||
用来拟合的四个系数是函数在基函数峰值位置的采样值:
|
||||
|
||||
$$
|
||||
\begin{align*}
|
||||
c_0 &= f(0) = \sin(0) = 0 \\
|
||||
c_1 &= f(1) = \sin\left(\frac{\pi}{4}\right) \approx 0.7071 \\
|
||||
c_2 &= f(2) = \sin\left(\frac{\pi}{2}\right) = 1 \\
|
||||
c_3 &= f(3) = \sin\left(\frac{3\pi}{4}\right) \approx 0.7071 \\
|
||||
\end{align*}
|
||||
$$
|
||||
|
||||
## 拟合曲线构造
|
||||
|
||||
最终的B样条拟合曲线是基函数的线性组合:
|
||||
|
||||
$$
|
||||
S(t) = 0 \cdot B_0(t) + 0.7071 \cdot B_1(t) + 1 \cdot B_2(t) + 0.7071 \cdot B_3(t)
|
||||
$$
|
||||
|
||||
## 可视化建议
|
||||
|
||||
需要展示以下内容吗?
|
||||
1. 原始函数 $f(t) = \sin(\pi t/4)$ 的曲线
|
||||
2. 四个采样点 $(0,0)$, $(1,0.7071)$, $(2,1)$, $(3,0.7071)$
|
||||
3. 每个基函数 $B_i(t)$ 及其对应的系数 $c_i$
|
||||
4. 最终合成的紫色B样条曲线 $S(t)$
|
||||
|
||||
---
|
||||
|
||||
## 公式列表(Markdown 格式)
|
||||
|
||||
> **注意**:以下公式与论文中编号对应(如 (1)、(2)、(3)、(4)、(5)、(6) 等)。
|
||||
|
||||
1. **注意力系数(未归一化)**
|
||||
$$
|
||||
e_{ij} = a\bigl(W\mathbf{h}_i,\; W\mathbf{h}_j\bigr)
|
||||
$$
|
||||
|
||||
2. **注意力系数的 softmax 归一化**
|
||||
$$
|
||||
\alpha_{ij} = \text{softmax}_j\bigl(e_{ij}\bigr)
|
||||
= \frac{\exp\bigl(e_{ij}\bigr)}{\sum_{k \in \mathcal{N}_i} \exp\bigl(e_{ik}\bigr)}
|
||||
$$
|
||||
|
||||
$\alpha_{ij}$表示节点 $i$ 对节点 $j$ 的注意力权重
|
||||
|
||||
3. **具体的注意力计算形式(以单层前馈网络 + LeakyReLU 为例)**
|
||||
|
||||
$$
|
||||
\alpha_{ij}
|
||||
= \frac{\exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_j\bigr]\bigr)\Bigr)}
|
||||
{\sum_{k\in \mathcal{N}_i} \exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_k\bigr]\bigr)\Bigr)}
|
||||
$$
|
||||
|
||||
其中,$\mathbf{a}$ 为可学习的参数向量,$\|$ 表示向量拼接(concatenation)。
|
||||
|
||||
4. **单头注意力聚合(得到新的节点特征)**
|
||||
$$
|
||||
\mathbf{h}_i' = \sigma\Bigl(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \,W \mathbf{h}_j\Bigr)
|
||||
$$
|
||||
|
||||
其中,$\sigma$ 表示非线性激活函数(如 ELU、ReLU 等),$\mathcal{N}_i$ 表示节点 $i$ 的邻居节点集合(可包含 $i$ 自身)。
|
||||
|
||||
5. **多头注意力(隐藏层时拼接)**
|
||||
如果有 $K$ 个独立的注意力头,每个头输出 $\mathbf{h}_i'^{(k)}$,则拼接后的输出为:
|
||||
$$
|
||||
\mathbf{h}_i' =
|
||||
\big\Vert_{k=1}^K
|
||||
\sigma\Bigl(\sum_{j \in \mathcal{N}_i} \alpha_{ij}^{(k)} \, W^{(k)} \mathbf{h}_j\Bigr)
|
||||
$$
|
||||
其中,$\big\Vert$ 表示向量拼接操作,$\alpha_{ij}^{(k)}$、$W^{(k)}$ 分别为第 $k$ 个注意力头对应的注意力系数和线性变换。
|
||||
|
||||
6. **多头注意力(输出层时平均)**
|
||||
在最终的输出层(例如分类层)通常会将多个头的结果做平均,而不是拼接:
|
||||
$$
|
||||
\mathbf{h}_i' =
|
||||
\sigma\Bigl(
|
||||
\frac{1}{K} \sum_{k=1}^K \sum_{j \in \mathcal{N}_i}
|
||||
\alpha_{ij}^{(k)} \, W^{(k)} \mathbf{h}_j
|
||||
\Bigr)
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
以上即是论文中 2.1 节(Graph Attentional Layer)出现的主要公式及其简要说明。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 2. **GAT 的聚合方式**
|
||||
|
||||
- **GAT** 使用了一种**自适应的、可学习的注意力机制**来聚合节点及其邻居的信息。
|
||||
- 具体来说,GAT 的聚合公式为:
|
||||
$$
|
||||
h_i^{(l+1)} = \sigma\left(\sum_{j \in \mathcal{N}(i) \cup \{i\}} \alpha_{ij} W h_j^{(l)}\right)
|
||||
$$
|
||||
其中:
|
||||
- $\alpha_{ij}$ 是节点 $i$ 和节点 $j$ 之间的**注意力系数**,通过以下方式计算:
|
||||
$$
|
||||
\alpha_{ij} = \frac{\exp(\text{LeakyReLU}(a^T [W h_i \| W h_j]))}{\sum_{k \in \mathcal{N}(i) \cup \{i\}} \exp(\text{LeakyReLU}(a^T [W h_i \| W h_k]))}
|
||||
$$
|
||||
- $a$ 是一个可学习的注意力向量。
|
||||
- $\|$ 表示特征拼接操作。
|
||||
- $W$ 是可学习的权重矩阵。
|
||||
- $\sigma$ 是非线性激活函数。
|
||||
|
||||
- **特点**:
|
||||
- GAT 的聚合权重是**动态的**,通过注意力机制学习得到。
|
||||
- 权重是非对称的,且可以捕捉节点之间的复杂关系。
|
||||
- 相当于对节点及其邻居进行了一种**加权信息传递**,权重由数据驱动。
|
||||
|
||||
---
|
||||
|
||||
### 3. **GCN 和 GAT 的对比**
|
||||
| 特性 | GCN | GAT |
|
||||
| ------------------ | ------------------------ | -------------------------- |
|
||||
| **聚合方式** | 固定的加权平均 | 自适应的注意力加权 |
|
||||
| **权重是否可学习** | 否(权重由节点度数决定) | 是(通过注意力机制学习) |
|
||||
| **权重是否对称** | 是 | 否 |
|
||||
| **表达能力** | 较弱(固定的聚合方式) | 较强(动态的聚合方式) |
|
||||
| **计算复杂度** | 较低 | 较高(需要计算注意力系数) |
|
||||
| **适用场景** | 简单的图结构任务 | 复杂的图结构任务 |
|
||||
|
||||
---
|
||||
|
||||
### 4. **直观理解**
|
||||
- **GCN**:
|
||||
- 类似于对邻居节点进行“民主投票”,每个邻居的权重是固定的(由度数决定)。
|
||||
- 适合处理节点度数分布均匀、关系相对简单的图。
|
||||
|
||||
- **GAT**:
|
||||
- 类似于对邻居节点进行“加权投票”,每个邻居的权重是动态学习的。
|
||||
- 适合处理节点度数分布不均匀、关系复杂的图。
|
||||
|
||||
---
|
||||
|
||||
### 5. **总结**
|
||||
- **GCN** 使用的是**固定的、归一化的加权平均**,权重由节点度数决定。
|
||||
- **GAT** 使用的是**自适应的、可学习的注意力权重**,权重通过数据驱动的方式学习得到。
|
||||
- GAT 的表达能力更强,但计算复杂度也更高;GCN 更简单高效,但表达能力相对较弱。
|
||||
|
||||
希望这个解释能帮助你更好地理解 GCN 和 GAT 的区别!如果还有疑问,欢迎继续讨论!
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们可以通过一个简单的例子来说明多头注意力拼接的计算过程。假设有两个注意力头($K=2$),且我们考虑一个节点 $i$ 以及它的两个邻居 $j=1$ 和 $j=2$。我们假设每个节点的输入特征 $\mathbf{h}_j$ 是一个二维向量,并且每个注意力头的线性变换 $W^{(k)}$ 将输入保持为二维(这里为了简化,取 $W^{(1)}$ 为单位矩阵,而 $W^{(2)}$ 为一个放大2倍的矩阵)。另外,我们假设各头对应的注意力权重(归一化后的)如下:
|
||||
|
||||
- **注意力头1:**
|
||||
- $\alpha_{i1}^{(1)} = 0.6$
|
||||
- $\alpha_{i2}^{(1)} = 0.4$
|
||||
|
||||
- **注意力头2:**
|
||||
- $\alpha_{i1}^{(2)} = 0.3$
|
||||
- $\alpha_{i2}^{(2)} = 0.7$
|
||||
|
||||
同时设定节点特征为:
|
||||
- $\mathbf{h}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$
|
||||
- $\mathbf{h}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$
|
||||
|
||||
下面按照每个注意力头计算节点 $i$ 的新特征,再进行拼接:
|
||||
|
||||
---
|
||||
|
||||
### 注意力头 1 的计算
|
||||
|
||||
- **线性变换:**
|
||||
$W^{(1)}$ 为单位矩阵,所以
|
||||
$$
|
||||
W^{(1)}\mathbf{h}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix},\quad W^{(1)}\mathbf{h}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
- **加权求和:**
|
||||
对邻居加权求和得到
|
||||
$$
|
||||
\sum_{j\in\mathcal{N}_i} \alpha_{ij}^{(1)} \, W^{(1)}\mathbf{h}_j
|
||||
= 0.6\begin{bmatrix} 1 \\ 0 \end{bmatrix} + 0.4\begin{bmatrix} 0 \\ 1 \end{bmatrix}
|
||||
= \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
- **非线性激活:**
|
||||
假设激活函数 $\sigma$ 是 ReLU,则
|
||||
$$
|
||||
\mathbf{h}_i'^{(1)} = \sigma\left(\begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix}\right)
|
||||
= \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### 注意力头 2 的计算
|
||||
|
||||
- **线性变换:**
|
||||
假设 $W^{(2)}$ 为将输入放大2倍的矩阵,即
|
||||
$$
|
||||
W^{(2)} = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}.
|
||||
$$
|
||||
则有
|
||||
$$
|
||||
W^{(2)}\mathbf{h}_1 = \begin{bmatrix} 2 \\ 0 \end{bmatrix},\quad W^{(2)}\mathbf{h}_2 = \begin{bmatrix} 0 \\ 2 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
- **加权求和:**
|
||||
使用注意力权重
|
||||
$$
|
||||
\sum_{j\in\mathcal{N}_i} \alpha_{ij}^{(2)} \, W^{(2)}\mathbf{h}_j
|
||||
= 0.3\begin{bmatrix} 2 \\ 0 \end{bmatrix} + 0.7\begin{bmatrix} 0 \\ 2 \end{bmatrix}
|
||||
= \begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
- **非线性激活:**
|
||||
同样使用 ReLU 激活
|
||||
$$
|
||||
\mathbf{h}_i'^{(2)} = \sigma\left(\begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}\right)
|
||||
= \begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### 拼接最终输出
|
||||
|
||||
将两个头的输出在特征维度上进行拼接,得到最终节点 $i$ 的新特征表示:
|
||||
$$
|
||||
\mathbf{h}_i' = \mathbf{h}_i'^{(1)} \,\Vert\, \mathbf{h}_i'^{(2)}
|
||||
= \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} \,\Vert\, \begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}
|
||||
= \begin{bmatrix} 0.6 \\ 0.4 \\ 0.6 \\ 1.4 \end{bmatrix}.
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
### 总结
|
||||
|
||||
- 每个注意力头独立计算:先用各自的线性变换 $W^{(k)}$ 对邻居节点特征进行转换,再用对应的注意力系数 $\alpha_{ij}^{(k)}$ 加权求和,最后经过非线性激活 $\sigma$ 得到输出 $\mathbf{h}_i'^{(k)}$。
|
||||
- 最后将所有 $K$ 个头的输出通过拼接操作合并成最终的节点特征表示 $\mathbf{h}_i'$。
|
||||
|
||||
这个例子展示了多头注意力机制如何通过多个独立的注意力头捕捉不同的子空间特征,最后将它们合并形成更丰富的表示。
|
||||
|
||||
|
||||
|
||||
这种构造方式展示了B样条的一个重要特性:**系数直接对应曲线在基函数峰值位置的值**(当基函数是标准归一化时)。
|
||||
|
||||
@ -34,10 +34,6 @@
|
||||
|
||||
|
||||
|
||||
# GNN
|
||||
|
||||
|
||||
|
||||
### 矢量量化
|
||||
|
||||
矢量量化的基本思想是将输入数据点视为多维向量,并将其映射到一个码本(codebook)中的最接近的码字。码本是预先确定的一组离散的向量,通常通过无监督学习方法(如**K-means**)从大量训练数据中得到。在矢量量化中,输入数据点与码本中的码字之间的距离度量通常使用**欧氏距离**。通过选择最接近的码字作为量化结果,可以用较少的码字表示输入数据,从而实现数据的压缩。同一个码字能够代表多个相似的多维向量,从而实现了**多对一的映射**。
|
||||
|
||||
@ -572,6 +572,8 @@ http://localhost:880/user/1/0
|
||||
|
||||
上述的这种传递请求参数的形式呢,我们称之为:路径参数。
|
||||
|
||||
注意,路径参数使用大括号 `{}` 定义
|
||||
|
||||
```java
|
||||
@RestController
|
||||
public class RequestController {
|
||||
@ -1129,6 +1131,8 @@ public class SpringbootWebConfig2Application {
|
||||
|
||||
**3.使用第三方依赖@EnableXxxx 注解**
|
||||
|
||||
如果第三方依赖没有提供自动配置支持,
|
||||
|
||||
常见方案是第三方依赖提供一个 `@EnableXxxx` 注解,这个注解内部封装了 `@Import`,通过它可以一次性导入多个配置或 Bean。
|
||||
|
||||
~~~java
|
||||
@ -1186,12 +1190,12 @@ public class SpringbootWebConfig2Application {
|
||||
}
|
||||
```
|
||||
|
||||
1. `@RequestBody`:这是一个**方法参数级别**的注解,用于告诉Spring框架将请求体的内容**解析为指定的Java对象**。
|
||||
1. `@RequestBody`:这是一个**方法参数级别**的注解,用于告诉Spring框架将请求体的内容解析为指定的**Java对象**。
|
||||
|
||||
2. `@RestController`:这是一个类级别的注解,它告诉Spring框架这个类是一个控制器(Controller),并且处理HTTP请求并返回响应数据。与 `@Controller` 注解相比,`@RestController` 注解还会自动将控制器方法返回的数据转换为 JSON 格式,并写入到HTTP响应中,得益于`@ResponseBody` 。
|
||||
`@RestController = @Controller + @ResponseBody`
|
||||
|
||||
4. `@PathVariable` 注解用于将路径变量 `{id}` 的值绑定到方法的参数 `id` 上。当请求的路径是 "/path/123" 时,`@PathVariable` 会将路径中的 "123" 值绑定到方法的参数 `id` 上,使得方法能够获取到这个值。在这个例子中,方法的参数 `id` 的值将会是整数值 123。
|
||||
4. `@PathVariable` 注解用于将路径参数 `{id}` 的值绑定到方法的参数 `id` 上。当请求的路径是 "/path/123" 时,`@PathVariable` 会将路径中的 "123" 值绑定到方法的参数 `id` 上。
|
||||
|
||||
```java
|
||||
public String pathParam(@PathVariable Integer id) {
|
||||
@ -1199,18 +1203,15 @@ public class SpringbootWebConfig2Application {
|
||||
return "OK";
|
||||
}
|
||||
|
||||
参数名与路径名不同
|
||||
//参数名与路径名不同
|
||||
@GetMapping("/{id}")
|
||||
public ResponseEntity<User> getUserById(@PathVariable("id") Long userId) {
|
||||
}
|
||||
public ResponseEntity<User> getUserById(@PathVariable("id") Long userId) {
|
||||
}
|
||||
```
|
||||
|
||||
5. `@RequestParam`,如果方法的参数名与请求参数名不同,需要在 `@RequestParam` 注解中指定请求参数的名字。
|
||||
|
||||
```java
|
||||
@RequestParam(defaultValue = "1" Integer page) //若page为null,可以设置page的默认值为1
|
||||
```
|
||||
|
||||
类似`@PathVariable`,可以指定参数名称。
|
||||
|
||||
```java
|
||||
@RequestMapping("/example")
|
||||
public String exampleMethod(@RequestParam String name, @RequestParam("age") int userAge) {
|
||||
@ -1220,20 +1221,20 @@ public class SpringbootWebConfig2Application {
|
||||
return "OK";
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
5. 控制反转与依赖注入:
|
||||
|
||||
`@Component` ,控制反转
|
||||
`@Component` ,`@Service`, `@Repository`控制反转
|
||||
|
||||
`@Autowired`,依赖注入
|
||||
`@Autowired`,`@Configuration` ,`@Bean`依赖注入
|
||||
|
||||
6. **数据库相关。**@Mapper注解:表示是mybatis中的Mapper接口
|
||||
|
||||
- 程序运行时:框架会自动生成接口的实现类对象(代理对象),并给交Spring的IOC容器管理
|
||||
程序运行时:框架会自动生成接口的实现类对象(代理对象),**并交给Spring的IOC容器管理**
|
||||
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
|
||||
7. @SpringBootTest:它会启动 Spring 应用程序上下文,并在测试期间模拟运行整个 Spring Boot 应用程序。这意味着你可以在集成测试中使用 Spring 的各种功能,例如**自动装配、依赖注入、配置加载**等。
|
||||
|
||||
|
||||
@ -162,12 +162,23 @@ IDEA快捷键:
|
||||
基本数据类型(Primitives)
|
||||
|
||||
- 传递方式:按值传递
|
||||
每次传递的是变量的值的副本,对该值的修改不会影响原变量。例如:`int`、`double`、`boolean` 等类型。
|
||||
每次传递的是变量的值的副本**,对该值的修改不会影响原变量**。例如:`int`、`double`、`boolean` 等类型。
|
||||
|
||||
引用类型(对象)
|
||||
|
||||
- 传递方式:对象引用的副本传递
|
||||
传递的是对象引用的一个副本,指向同一块内存区域。因此,方法内部通过该引用修改对象的状态,会影响到原对象。如数组、集合、String、以及其他所有对象类型。
|
||||
传递的是对象引用的一个副本,**指向同一块内存区域**。因此,方法内部通过该引用修改对象的状态,会影响到原对象。如数组、集合、String、以及其他所有对象类型。
|
||||
|
||||
注意
|
||||
|
||||
```java
|
||||
StringBuilder s = new StringBuilder();
|
||||
s.append("hello");
|
||||
String res = s.toString(); // res = "hello"
|
||||
|
||||
s.append(" world"); // s = "hello world"
|
||||
System.out.println(res); // 输出还是 "hello"
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
139
自学/力扣Hot 100题.md
139
自学/力扣Hot 100题.md
@ -91,8 +91,6 @@ String sortedStr = new String(charArray);
|
||||
|
||||
`StringBuffer` 是 Java 中用于操作可变字符串的类
|
||||
|
||||
**append**
|
||||
|
||||
```java
|
||||
public class StringBufferExample {
|
||||
public static void main(String[] args) {
|
||||
@ -124,6 +122,13 @@ public class StringBufferExample {
|
||||
}
|
||||
```
|
||||
|
||||
StringBuffer有库函数可以翻转,String未提供!
|
||||
|
||||
```java
|
||||
StringBuilder sb = new StringBuilder(s);
|
||||
String reversed = sb.reverse().toString();
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### `HashMap`
|
||||
@ -315,6 +320,26 @@ public class PriorityQueueExample {
|
||||
- 访问元素的时间复杂度为 O(1),在末尾插入和删除的时间复杂度为 O(1)。
|
||||
- 在指定位置插入和删除O(n) `add(int index, E element)` `remove(int index)`
|
||||
|
||||
复制链表(list set queue都有addAll方法,map是putAll):
|
||||
|
||||
```java
|
||||
List<Integer> list1 = new ArrayList<>();
|
||||
// 假设 list1 中已有数据
|
||||
List<Integer> list2 = new ArrayList<>();
|
||||
list2.addAll(list1); //法一
|
||||
List<Integer> list2 = new ArrayList<>(list1); //法二
|
||||
```
|
||||
|
||||
清空(list set map queue map都有clear方法):
|
||||
|
||||
```java
|
||||
List<Integer> list = new ArrayList<>();
|
||||
// 清空 list
|
||||
list.clear();
|
||||
```
|
||||
|
||||
|
||||
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.List;
|
||||
@ -712,49 +737,6 @@ public class ListSortExample {
|
||||
- 如果返回零,说明 `o1` 等于 `o2`。
|
||||
- 如果返回正数,说明 `o1` 排在 `o2`后面。
|
||||
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.Collections;
|
||||
import java.util.Comparator;
|
||||
import java.util.List;
|
||||
|
||||
class Person {
|
||||
String name;
|
||||
int age;
|
||||
|
||||
public Person(String name, int age) {
|
||||
this.name = name;
|
||||
this.age = age;
|
||||
}
|
||||
|
||||
@Override
|
||||
public String toString() {
|
||||
return name + " (" + age + ")";
|
||||
}
|
||||
}
|
||||
|
||||
public class ComparatorSortExample {
|
||||
public static void main(String[] args) {
|
||||
// 创建一个 Person 列表
|
||||
List<Person> people = new ArrayList<>();
|
||||
people.add(new Person("Alice", 25));
|
||||
people.add(new Person("Bob", 20));
|
||||
people.add(new Person("Charlie", 30));
|
||||
|
||||
// 使用 Comparator 按姓名排序
|
||||
Collections.sort(people, new Comparator<Person>() {
|
||||
@Override
|
||||
public int compare(Person p1, Person p2) {
|
||||
return p1.name.compareTo(p2.name); // 按姓名升序排序
|
||||
}
|
||||
});
|
||||
|
||||
// 输出排序后的列表
|
||||
System.out.println(people); // 输出 [Alice (25), Bob (20), Charlie (30)]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**自定义比较器排序二维数组** 用Lambda表达式实现`Comparator<int[]>接口`
|
||||
@ -785,8 +767,75 @@ public class IntervalSort {
|
||||
|
||||
|
||||
|
||||
对象排序,不用lambda方式
|
||||
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.Collections;
|
||||
import java.util.Comparator;
|
||||
import java.util.List;
|
||||
|
||||
class Person {
|
||||
String name;
|
||||
int age;
|
||||
|
||||
public Person(String name, int age) {
|
||||
this.name = name;
|
||||
this.age = age;
|
||||
}
|
||||
|
||||
@Override
|
||||
public String toString() {
|
||||
return name + " (" + age + ")";
|
||||
}
|
||||
}
|
||||
|
||||
public class ComparatorSortExample {
|
||||
public static void main(String[] args) {
|
||||
// 创建一个 Person 列表
|
||||
List<Person> people = new ArrayList<>();
|
||||
people.add(new Person("Alice", 25));
|
||||
people.add(new Person("Bob", 20));
|
||||
people.add(new Person("Charlie", 30));
|
||||
|
||||
// 使用 Comparator 按姓名排序,匿名内部类形式
|
||||
Collections.sort(people, new Comparator<Person>() {
|
||||
@Override
|
||||
public int compare(Person p1, Person p2) {
|
||||
return p1.name.compareTo(p2.name); // 按姓名升序排序
|
||||
}
|
||||
});
|
||||
|
||||
// 使用 Comparator 按姓名排序,使用 lambda 表达式
|
||||
//Collections.sort(people, (p1, p2) -> p1.name.compareTo(p2.name));
|
||||
|
||||
// 输出排序后的列表
|
||||
System.out.println(people); // 输出 [Alice (25), Bob (20), Charlie (30)]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 题型
|
||||
|
||||
常见术语:
|
||||
|
||||
子串(Substring):子字符串 是字符串中连续的 非空 字符序列
|
||||
|
||||
回文串(Palindrome):回文 串是向前和向后读都相同的字符串。
|
||||
|
||||
子序列((Subsequence)):可以通过删除原字符串中任意个字符(不改变剩余字符的相对顺序)得到的序列,不要求连续。例如 "abc" 的 "ac" 就是一个子序列。
|
||||
|
||||
前缀 (Prefix) :从字符串起始位置开始的连续字符序列,如 "leetcode" 的前缀 "lee"。
|
||||
|
||||
字母异位词 (Anagram):由相同字符组成但排列顺序不同的字符串。例如 "abc" 与 "cab" 就是异位词。
|
||||
|
||||
子集、幂集:数组的 子集 是从数组中选择一些元素(可能为空)。例如,对于集合 S = {1, 2},其幂集为:
|
||||
{ ∅, {1}, {2}, {1, 2} },子集有{1}
|
||||
|
||||
|
||||
|
||||
#### 哈希
|
||||
|
||||
**问题分析**:
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user