zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Commit on 2025/03/23 周日 16:39:22.08

Browse Source
This commit is contained in:
zhangsan 2025-03-23 16:39:22 +08:00
parent 6722fcea38
commit 7eaec483da
6 changed files with 1084 additions and 515 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

9
Java/git基本操作.md
View File

@ -356,12 +356,15 @@ git config --global credential.helper store //将凭据保存到磁盘上（明
**如果不小心commit了如何撤销？** **如果不小心commit了如何撤销？**
到项目根目录，git bash here 例：如果在添加`.gitignore`文件前不小心提交了`.idea`文件夹，到项目根目录，git bash here
```text ```text
git rm -r --cached 'dictory'/ git rm -r --cached -f .idea
git commit -m "Remove .idea from tracking"
``` ```
![](https://pic.bitday.top/i/2025/03/19/u68fal-2.png)在.gitignore文件进行添加 ![](https://pic.bitday.top/i/2025/03/19/u68fal-2.png)在.gitignore文件进行添加
**为什么`.gitignore`文件不放在`.git`文件夹中？** **为什么`.gitignore`文件不放在`.git`文件夹中？**
@ -371,8 +374,6 @@ git rm -r --cached 'dictory'/
### 撤销Git版本控制 ### 撤销Git版本控制
直接把项目文件夹中的.git文件夹删除即可(开启查看隐藏文件夹可看到) 直接把项目文件夹中的.git文件夹删除即可(开启查看隐藏文件夹可看到)

55
Java/linux服务器.md
View File

@ -989,21 +989,12 @@ rm -rf /root/data/docker_data/typecho # 完全删除映射到本地的数据
### 主题
Joe主题：https://github.com/HaoOuBa/Joe Joe主题：https://github.com/HaoOuBa/Joe
[Joe再续前缘主题 - 搭建本站同款网站 - 易航博客](https://blog.yihang.info/archives/18.html) [Joe再续前缘主题 - 搭建本站同款网站 - 易航博客](https://blog.yihang.info/archives/18.html)
markdown编辑器插件：https://xiamp.net/archives/aaeditor-is-another-typecho-editor-plugin.html
- 关闭'开启公式显示'，将公式渲染交给markdownParse
markdown解析器插件：[mrgeneralgoo/typecho-markdown: A markdown parse plugin for typecho.](https://github.com/mrgeneralgoo/typecho-markdown)
- 确保代码块\```后面紧跟着语言，如\```java，否则无法正确显示。
- 确保公式块$$是
修改文章详情页的上方信息： 修改文章详情页的上方信息：
`typecho/usr/themes/Joe/module/single/batten.php` `typecho/usr/themes/Joe/module/single/batten.php`
@ -1057,6 +1048,48 @@ if (!defined('__TYPECHO_ROOT_DIR__')) {
`typecho/usr/themes/Joe/assets/js/joe.single.js`原版： 显示弹窗，点叉后消失
```text
{
document.querySelector('.joe_detail__article').addEventListener('copy', () => {
autolog.log(`本文版权属于 ${Joe.options.title} 转载请标明出处！`, 'warn', false);
});
}
```
显示5秒后消失：
```
document.querySelector('.joe_detail__article').addEventListener('copy', () => {
// 显示 autolog 消息
autolog.log(`本文版权属于 ${Joe.options.title} 转载请标明出处！`, 'warn', false);
// 5 秒后删除该消息
setTimeout(() => {
const warnElem = document.querySelector('.autolog-warn');
if (warnElem) {
warnElem.remove(); // 或者使用 warnElem.style.display = 'none';
}
}, 5000);
});
```
### **markdown编辑与解析**
确保代码块\```后面紧跟着语言，如\```java，否则无法正确显示。
markdown编辑器插件：https://xiamp.net/archives/aaeditor-is-another-typecho-editor-plugin.html
- '开启公式显示！'
markdown解析器插件：[mrgeneralgoo/typecho-markdown: A markdown parse plugin for typecho.](https://github.com/mrgeneralgoo/typecho-markdown)
- 有bug，暂时废弃。
slug为页面缩略名，在新增文章时可以传入，默认是index数字。 slug为页面缩略名，在新增文章时可以传入，默认是index数字。
![image-20250320185818633](https://pic.bitday.top/i/2025/03/20/uqbaps-0.png) ![image-20250320185818633](https://pic.bitday.top/i/2025/03/20/uqbaps-0.png)

111
科研/图神经网络.md
View File

@ -285,7 +285,116 @@ $$
### GNN的优点： ## GAT
图注意力网络（GAT）中最核心的运算：**图注意力层**。它的基本思想是：
1. **线性变换**：先对每个节点的特征 $\mathbf{h}_i$ 乘上一个可学习的权重矩阵 $W$，得到变换后的特征 $W \mathbf{h}_i$。
2. **自注意力机制**：通过一个可学习的函数 $a$，对节点 $i$ 和其邻居节点 $j$ 的特征进行计算，得到注意力系数 $e_{ij}$。这里会对邻居进行遮蔽（masked attention），即只计算图中有边连接的节点对。
3. **归一化**：将注意力系数 $e_{ij}$ 通过 softmax 进行归一化，得到 $\alpha_{ij}$，表示节点 $j$ 对节点 $i$ 的重要性权重。
4. **聚合**：最后利用注意力系数加权邻居节点的特征向量，并经过激活函数得到新的节点表示 $\mathbf{h}_i'$。
5. **多头注意力**：为增强表示能力，可并行地执行多个独立的注意力头（multi-head attention），再将它们的结果进行拼接（或在最后一层进行平均），从而得到最终的节点表示。
### 注意力系数
1. **注意力系数（未归一化）**
$$
e_{ij} = a\bigl(W\mathbf{h}_i,\; W\mathbf{h}_j\bigr)
$$
2. **注意力系数的 softmax 归一化**
$$
\alpha_{ij} = \text{softmax}_j\bigl(e_{ij}\bigr)
= \frac{\exp\bigl(e_{ij}\bigr)}{\sum_{k \in \mathcal{N}_i} \exp\bigl(e_{ik}\bigr)}
$$
3. **具体的注意力计算形式（以单层前馈网络 + LeakyReLU 为例）**
$$
\alpha_{ij}
= \frac{\exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_j\bigr]\bigr)\Bigr)}
{\sum_{k\in \mathcal{N}_i} \exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_k\bigr]\bigr)\Bigr)}
$$
- 其中，$\mathbf{a}$ 为可学习的参数向量，$\|$ 表示向量拼接（concatenation）。
**示例假设：**
- **节点特征**：
假设每个节点的特征向量维度为 $F=2$。
$$
\mathbf{h}_i = \begin{bmatrix}1 \\ 0\end{bmatrix},\quad
\mathbf{h}_j = \begin{bmatrix}0 \\ 1\end{bmatrix},\quad
\mathbf{h}_k = \begin{bmatrix}1 \\ 1\end{bmatrix}.
$$
- **线性变换矩阵 $W$**：
为了简化，我们令 $W$ 为单位矩阵（即 $W\mathbf{h} = \mathbf{h}$）。
$$
W = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}.
$$
- **可学习向量 $\mathbf{a}$**：
假设 $\mathbf{a}$ 为 4 维向量，设
$$
\mathbf{a} = \begin{bmatrix}1 \\ 1 \\ 1 \\ 1\end{bmatrix}.
$$
- 激活函数使用 LeakyReLU（负斜率设为0.2，但本例中结果为正数，所以不变）。
---
**计算步骤：**
1. **计算 $W\mathbf{h}_i$、$W\mathbf{h}_j$ 和 $W\mathbf{h}_k$：**
$$
W\mathbf{h}_i = \begin{bmatrix}1 \\ 0\end{bmatrix},\quad
W\mathbf{h}_j = \begin{bmatrix}0 \\ 1\end{bmatrix}, \quad
W\mathbf{h}_k = \begin{bmatrix}1 \\ 1\end{bmatrix}
$$
2. **构造拼接向量并计算未归一化的注意力系数 $e_{ij}$ 和 $e_{ik}$：**
- 对于邻居 $j$：
$$
\bigl[W\mathbf{h}_i \,\|\, W\mathbf{h}_j\bigr] =
\begin{bmatrix}1 \\ 0 \\ 0 \\ 1\end{bmatrix}.
$$
内积计算：
$$
\mathbf{a}^\top \begin{bmatrix}1 \\ 0 \\ 0 \\ 1\end{bmatrix} = 1+0+0+1 = 2.
$$
经过 LeakyReLU（正数保持不变）：
$$
e_{ij} = 2.
$$
- 对于邻居 $k$,同理得到：
$$
e_{ik} = 3.
$$
3. **计算 softmax 得到归一化注意力系数 $\alpha_{ij}$：**
$$
\alpha_{ij} = \frac{\exp(2)}{\exp(2)+\exp(3)} = \frac{e^2}{e^2+e^3}\approx 0.269.
$$
同理：
$$
\alpha_{ik} = \frac{\exp(3)}{\exp(2)+\exp(3)} \approx 0.731.
$$
## GNN的优点：
**参数共享** **参数共享**

511
科研/数学基础.md
View File

@ -487,517 +487,40 @@ $$
## 拉普拉斯变换 ## 拉普拉斯变换
![image-20240413112801149](https://pic.bitday.top/i/2025/03/19/u8f2b5-2.png) ### 拉普拉斯变换的定义
## 矩阵运算 对于一个给定的时间域函数 \( f(t) \)，其拉普拉斯变换 \( F(s) \) 定义为：
### 特征值和特征向量
设矩阵：
$$
A = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}
$$
步骤 1：求特征值
构造特征方程：
$$
\det(A - \lambda I) = \det\begin{bmatrix} 2-\lambda & 1 \\ 0 & 3-\lambda \end{bmatrix} = (2-\lambda)(3-\lambda) - 0 = 0
$$
解得：
$$ $$
(2-\lambda)(3-\lambda) = 0 \quad \Longrightarrow \quad \lambda_1 = 2,\quad \lambda_2 = 3 F(s) = \int_{0}^{\infty} e^{-st}f(t) \, dt
$$ $$
步骤 2：求特征向量 这里的 \( s \) 是一个复数，通常写作 $ s = \sigma + j\omega $，其中 $\sigma$ 和 $ \omega $ 分别是实部和虚部。
- 对于 $\lambda_1 = 2$： ### 拉普拉斯变换的作用
解方程：
$$ - **简化微分方程**：拉普拉斯变换可以将微分方程转换为代数方程，从而简化求解过程。
(A - 2I)\mathbf{x} = \begin{bmatrix} 2-2 & 1 \\ 0 & 3-2 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_2 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} - **系统分析**：在控制理论中，拉普拉斯变换用来分析系统的稳定性和频率响应。
$$ - **信号处理**：在信号处理中，拉普拉斯变换帮助分析信号的频谱和系统的滤波特性。
从第一行 $x_2 = 0$。因此特征向量可以写成： ### 例子：单一指数函数的拉普拉斯变换
$$ 假设有一个函数 $f(t) = e^{-at} $（其中 \( a \) 是一个正常数），我们想计算它的拉普拉斯变换。根据拉普拉斯变换的定义：
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad (\text{任意非零常数倍})
$$
- 对于 $\lambda_2 = 3$：
解方程：
$$ $$
(A - 3I)\mathbf{x} = \begin{bmatrix} 2-3 & 1 \\ 0 & 3-3 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -x_1+x_2 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} F(s) = \int_{0}^{\infty} e^{-st}e^{-at} \, dt = \int_{0}^{\infty} e^{-(s+a)t} \, dt
$$
从第一行得 $-x_1 + x_2 = 0$ 或 $x_2 = x_1$。因此特征向量可以写成：
$$
\mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \quad (\text{任意非零常数倍})
$$
**设一个对角矩阵**：
$$
D = \begin{bmatrix} d_1 & 0 \\ 0 & d_2 \end{bmatrix}
$$
$$
\lambda_1 = d_1,\quad \lambda_2 = d_2
$$
对角矩阵的特征方程为：
$$
\det(D - \lambda I) = (d_1 - \lambda)(d_2 - \lambda) = 0
$$
因此特征值是：
$$ $$
\lambda_1 = d_1,\quad \lambda_2 = d_2
$$
- 对于 $\lambda_1 = d_1$，方程 $(D-d_1I)\mathbf{x}=\mathbf{0}$ 得到：
$$
\begin{bmatrix} 0 & 0 \\ 0 & d_2-d_1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ (d_2-d_1)x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
$$
若 $d_1 \neq d_2$，则必须有 $x_2=0$，而 $x_1$ 可任意取非零值，因此特征向量为：
$$
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}
$$
- 对于 $\lambda_2 = d_2$，类似地解得：
$$
\mathbf{v}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}
$$
### 矩阵乘法
**全连接神经网络**
![image-20250316145729703](https://pic.bitday.top/i/2025/03/19/u8fmco-2.png)
其中：
- $a^{(0)}$ 是输入向量，表示当前**层**的输入。
- $\mathbf{W}$ 是权重矩阵，表示输入向量到输出向量的线性变换。
- $b$ 是偏置向量，用于调整输出。
- $\sigma$ 是激活函数（如 ReLU、Sigmoid 等），用于引入非线性。
- **输入向量 $a^{(0)}$**：
$$
a^{(0)} = \begin{pmatrix}
a_0^{(0)} \\
a_1^{(0)} \\
\vdots \\
a_n^{(0)}
\end{pmatrix}
$$
这是一个 $n+1$ 维的列向量，表示输入特征。
- **权重矩阵 $\mathbf{W}$**：
$$
\mathbf{W} = \begin{pmatrix}
w_{0,0} & w_{0,1} & \cdots & w_{0,n} \\
w_{1,0} & w_{1,1} & \cdots & w_{1,n} \\
\vdots & \vdots & \ddots & \vdots \\
w_{k,0} & w_{k,1} & \cdots & w_{k,n} \\
\end{pmatrix}
$$
这是一个 $k \times (n+1)$ 的矩阵，其中 $k$ 是输出向量的维度，$n+1$ 是输入向量的维度。
- **偏置向量 $b$**：
$$
b = \begin{pmatrix}
b_0 \\
b_1 \\
\vdots \\
b_k
\end{pmatrix}
$$
这是一个 $k$ 维的列向量，用于调整输出。
1. 在传统的连续时间 RNN 写法里，常见的是
$$ 这个积分可以解为：
\sum_{j} W_{ij} \, \sigma(x_j),
$$
这代表对所有神经元 $j$ 的激活 $\sigma(x_j)$ 做加权求和，再求和到神经元 $i$。
如果拆开来看，每个输出分量也都含一个求和 $\sum_{j}$：
- 输出向量的第 1 个分量（记作第 1 行的结果）：
$$
(W_r x)_1 = 0.3 \cdot x_1 + (-0.5) \cdot x_2 = 0.3 \cdot 2 + (-0.5) \cdot 1 = 0.6 - 0.5 = 0.1.
$$
- 输出向量的第 2 个分量（第 2 行的结果）：
$$
(W_r x)_2 = 1.2 \cdot x_1 + 0.4 \cdot x_2 = 1.2 \cdot 2 + 0.4 \cdot 1 = 2.4 + 0.4 = 2.8.
$$
2. 在使用矩阵乘法时，你可以写成
$$
y = W_r \, \sigma(x),
$$
其中 $\sigma$ 表示对 $x$ 的各分量先做激活，接着用 $W_r$ 乘上去。这就是把“$\sum_j \dots$”用矩阵乘法隐藏了。
$$
\begin{pmatrix}
0.3 & -0.5\\
1.2 & \;\,0.4
\end{pmatrix}
\begin{pmatrix}
2\\
1
\end{pmatrix}
=
\begin{pmatrix}
0.3 \times 2 + (-0.5) \times 1\\[6pt]
1.2 \times 2 + 0.4 \times 1
\end{pmatrix}
=
\begin{pmatrix}
0.6 - 0.5\\
2.4 + 0.4
\end{pmatrix}
=
\begin{pmatrix}
0.1\\
2.8
\end{pmatrix}.
$$
### 奇异值
**定义**
对于一个 $m \times n$ 的矩阵 $A$，其奇异值是非负实数 $\sigma_1, \sigma_2, \ldots, \sigma_r$（$r = \min(m, n)$），满足存在正交矩阵 $U$ 和 $V$，使得：
$$
A = U \Sigma V^T
$$
其中，$\Sigma$ 是对角矩阵，对角线上的元素即为奇异值。
---
**主要特点**
1. **非负性**：奇异值总是非负的。
2. 对角矩阵的奇异值是对角线元素的**绝对值**。
3. **降序排列**：通常按从大到小排列，即 $\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_r \geq 0$。
4. **矩阵分解**：奇异值分解（SVD）将矩阵分解为三个矩阵的乘积，$U$ 和 $V$ 是正交矩阵，$\Sigma$ 是对角矩阵。
5. **应用广泛**：奇异值在数据降维、噪声过滤、图像压缩等领域有广泛应用。
---
**计算**
奇异值可以通过计算矩阵 $A^T A$ 或 $A A^T$ 的特征值的**平方根**得到。
**步骤 1：计算 $A^T A$**
首先，我们计算矩阵 $A$ 的转置 $A^T$：
$$
A^T = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix}
$$
然后，计算 $A^T A$：
$$
A^T A = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} = \begin{pmatrix} 9 & 0 \\ 0 & 16 \end{pmatrix}
$$
**步骤 2：计算 $A^T A$ 的特征值**
接下来，我们计算 $A^T A$ 的特征值。特征值 $\lambda$ 满足以下特征方程：
$$
\det(A^T A - \lambda I) = 0
$$
即：
$$
\det \begin{pmatrix} 9 - \lambda & 0 \\ 0 & 16 - \lambda \end{pmatrix} = (9 - \lambda)(16 - \lambda) = 0
$$
解这个方程，我们得到两个特征值：
$$
\lambda_1 = 16, \quad \lambda_2 = 9
$$
**步骤 3：计算奇异值**
奇异值是特征值的平方根，因此我们计算：
$$
\sigma_1 = \sqrt{\lambda_1} = \sqrt{16} = 4
$$
$$
\sigma_2 = \sqrt{\lambda_2} = \sqrt{9} = 3
$$
**结果**
矩阵 $A$ 的奇异值为 **4** 和 **3**。
### 矩阵的迹
**迹的定义**
对于一个 $n \times n$ 的矩阵 $B$，其迹（trace）定义为矩阵对角线元素之和：
$$
\text{tr}(B) = \sum_{i=1}^n B_{ii}
$$
**迹与特征值的关系**
对于一个 $n \times n$ 的矩阵 $B$，其迹等于其特征值之和。即：
$$
\text{tr}(B) = \sum_{i=1}^n \lambda_i
$$
其中 $\lambda_1, \lambda_2, \ldots, \lambda_n$ 是矩阵 $B$ 的特征值。
**应用到 $A^* A$**
对于矩阵 $A^* A$（如果 $A$ 是实矩阵，则 $A^* = A^T$），它是一个半正定矩阵，其特征值是非负实数。
$A^* A$ 的迹还与矩阵 $A$ 的 Frobenius 范数有直接关系。具体来说：
$$
\|A\|_F^2 = \text{tr}(A^* A)
$$
**迹的基本性质**
迹是一个线性运算，即对于任意标量 $c_1, c_2$ 和矩阵 $A, B$，有：
$$
\text{tr}(c_1 A + c_2 B) = c_1 \text{tr}(A) + c_2 \text{tr}(B)
$$
对于任意矩阵 $A, B, C$，迹满足循环置换性质：
$$
\text{tr}(ABC) = \text{tr}(CAB) = \text{tr}(BCA)
$$
注意：迹的循环置换性**不**意味着 $\text{tr}(ABC) = \text{tr}(BAC)$，除非矩阵 $A, B, C$ 满足某些特殊条件（如对称性）。
### 酉矩阵
酉矩阵是一种复矩阵，其满足下面的条件：对于一个 $n \times n$ 的复矩阵 $U$，如果有
$$
U^* U = U U^* = I,
$$
其中 $U^*$ 表示 $U$ 的共轭转置（先转置再取复共轭），而 $I$ 是 $n \times n$ 的单位矩阵，那么 $U$ 就被称为酉矩阵。简单来说，酉矩阵在复内积空间中保持内积不变，相当于在该空间中的“旋转”或“反射”。
如果矩阵的元素都是实数，那么 $U^*$ 就等于 $U^T$（转置），这时酉矩阵就退化为**正交矩阵**。
考虑二维旋转矩阵
$$
U = \begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}.
$$
当 $\theta$ 为任意实数时，这个矩阵满足
$$
U^T U = I,
$$
所以它是一个正交矩阵，同时也属于酉矩阵的范畴。
例如，当 $\theta = \frac{\pi}{4}$（45°）时，
$$
U = \begin{bmatrix}
\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}
\end{bmatrix}.
$$
### 对称非负矩阵分解
$$
A≈HH^T
$$
**1. 问题回顾**
给定一个**对称非负**矩阵 $A\in\mathbb{R}^{n\times n}$，我们希望找到一个**非负矩阵** $H\in\mathbb{R}^{n\times k}$ 使得
$$
A \approx HH^T.
$$
为此，我们可以**最小化目标函数(损失函数)**
$$
f(H)=\frac{1}{2}\|A-HH^T\|_F^2,
$$
其中 $\|\cdot\|_F$ 表示 Frobenius 范数，定义为矩阵所有元素的平方和的平方根。
$\| A - H H^T \|_F^2$ 表示矩阵 $A - H H^T$ 的所有元素的平方和。
**2. 梯度下降方法**
2.1 计算梯度
目标函数(损失函数)是
$$
f(H)=\frac{1}{2}\|A-HH^T\|_F^2.
$$
$$
\|M\|_F^2 = \operatorname{trace}(M^T M),
$$
因此，目标函数可以写成：
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^T\bigl(A-HH^T\bigr)\Bigr].
$$
注意到 $A$ 和$HH^T$ 都是对称矩阵，可以简化为：
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^2\Bigr].
$$
展开后得到
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[A^2 - 2AHH^T + (HH^T)^2\Bigr].
$$
其中 $\operatorname{trace}(A^2)$ 与 $H$ 无关，可以看作常数，不影响梯度计算。
**计算** $\nabla_H \operatorname{trace}(-2 A H H^T)$
$$
\nabla_H \operatorname{trace}(-2 A H H^T) = -4 A H
$$
**计算** $\nabla_H \operatorname{trace}((H H^T)^2)$
$$
\nabla_H \operatorname{trace}((H H^T)^2) = 4 H H^T H
$$
将两部分梯度合并：
$$
\nabla_H f(H) = \frac{1}{2}(4 H H^T H - 4 A H )= 2(H H^T H - A H)
$$
2.2 梯度下降更新
设学习率为 $\eta>0$，则梯度下降的**基本更新公式为**：
$$
H \leftarrow H - \eta\, \nabla_H f(H) = H - 2\eta\Bigl(HH^T H - A H\Bigr).
$$
由于我们要求 $H$ 中的元素保持非负，所以每次更新之后通常需要进行**投影**：
$$
H_{ij} \leftarrow \max\{0,\,H_{ij}\}.
$$
这种方法称为**投影梯度下降**，保证每一步更新后 $H$ 满足非负约束。
**3. 举例说明**
设对称非负矩阵：
$$
A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}, \quad k=1, \quad H \in \mathbb{R}^{2 \times 1}
$$
初始化 $H^{(0)} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$，学习率 $\eta = 0.01$。
**迭代步骤**：
1. **初始 \( H^{(0)} \):**
$$
H^{(0)} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}, \quad H^{(0)}(H^{(0)})^T = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}.
$$
目标函数值：
$$
f(H^{(0)}) = \frac{1}{2} \left( (2-1)^2 + 2(1-1)^2 + (2-1)^2 \right) = 1.
$$
2. **计算梯度：**
$$
HH^T H = \begin{bmatrix} 2 \\ 2 \end{bmatrix}, \quad AH = \begin{bmatrix} 3 \\ 3 \end{bmatrix},
$$
$$
\nabla_H f(H^{(0)}) = 2 \left( \begin{bmatrix} 2 \\ 2 \end{bmatrix} - \begin{bmatrix} 3 \\ 3 \end{bmatrix} \right) = \begin{bmatrix} -2 \\ -2 \end{bmatrix}.
$$
3. **更新 \( H \):**
$$
H^{(1)} = H^{(0)} - 2 \cdot 0.01 \cdot \begin{bmatrix} -2 \\ -2 \end{bmatrix} = \begin{bmatrix} 1.04 \\ 1.04 \end{bmatrix}.
$$
4. **更新后目标函数：**
$$
H^{(1)}(H^{(1)})^T = \begin{bmatrix} 1.0816 & 1.0816 \\ 1.0816 & 1.0816 \end{bmatrix},
$$
$$ $$
f(H^{(1)}) = \frac{1}{2} \left( (2-1.0816)^2 + 2(1-1.0816)^2 + (2-1.0816)^2 \right) \approx 0.8464. F(s) =
\begin{bmatrix}
\frac{e^{-(s+a)t}}{-(s+a)}
\end{bmatrix}_{0}^{\infty} = \frac{1}{s+a}
$$ $$
一次迭代后目标函数值从 $1.0$ 下降至 $0.8464$ 因为当 $ t \to \infty $ 时，$ e^{-(s+a)t} $ 趋向于 0，前提是 $ Re(s+a) > 0 $（即 $s $ 的实部加 $ a $ 必须是正的）。

723
科研/线性代数.md Normal file
View File

@ -0,0 +1,723 @@
## 线性代数
### 线性变换
每列代表一个基向量，行数代码这个基向量所张成空间的维度，二行三列表示二维空间的三个基向量。
- 二维标准基矩阵（单位矩阵）：
$$
\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | \\ \mathbf{i} & \mathbf{j} \\ | & | \end{bmatrix}
$$
- 三维标准基矩阵（单位矩阵）：
$$
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{i} & \mathbf{j} & \mathbf{k} \\ | & | & | \end{bmatrix}
$$
#### **矩阵乘向量**
在 3blue1brown 的“线性代数的本质”系列中，他把矩阵乘向量的运算解释为**线性组合**和**线性变换**的过程。具体来说：
- **计算方法**
给定一个 $ m \times n $ 的矩阵 $ A $ 和一个 $ n $ 维向量 $ \mathbf{x} = [x_1, x_2, \dots, x_n]^T $，矩阵与向量的乘积可以表示为：
$$
A\mathbf{x} = x_1 \mathbf{a}_1 + x_2 \mathbf{a}_2 + \cdots + x_n \mathbf{a}_n
$$
其中，$\mathbf{a}_i$ 表示 $ A $ 的第 $ i $ 列向量。也就是说，我们用向量 $\mathbf{x}$ 的各个分量作为权重，对矩阵的各列进行线性组合。
例如：矩阵 $ A $ 是一个二阶矩阵：
$$
A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
$$
向量 $ \mathbf{x} $ 是一个二维列向量：
$$
\mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix}
$$
可以将这个乘法看作是用 $ x $ 和 $ y $ 这两个数，分别对矩阵的两列向量进行加权：
$$
A\mathbf{x} = x \cdot \begin{bmatrix} a \\ c \end{bmatrix} + y \cdot \begin{bmatrix} b \\ d \end{bmatrix}
$$
也就是说，矩阵乘向量的结果，是“矩阵每一列”乘以“向量中对应的分量”，再把它们加起来。
- **背后的思想**
1. **分解为基向量的组合**：
任何向量都可以看作是标准基向量的线性组合。矩阵 $ A $ 在几何上代表了一个线性变换，而标准基向量在这个变换下会分别被映射到新的位置，也就是矩阵的各列。
2. **构造变换**：
当我们用 $\mathbf{x}$ 的分量对这些映射后的基向量加权求和时，就得到了 $ \mathbf{x} $ 在变换后的结果。这种方式不仅方便计算，而且直观地展示了线性变换如何“重塑”空间——每一列告诉我们基向量被如何移动，然后这些移动按比例组合出最终向量的位置。
#### **矩阵乘矩阵**
当你有两个矩阵 $ A $ 和 $ B $，矩阵乘法 $ AB $ 实际上代表的是：
> 先对向量应用 $ B $ 的线性变换，再应用 $ A $ 的线性变换。
也就是说：
$$
(AB)\vec{v} = A(B\vec{v})
$$
**3blue1brown 的直觉解释：**
矩阵 B：提供了新的**变换后基向量**
记住：矩阵的每一列，表示标准基向量 $ \mathbf{e}_1, \mathbf{e}_2 $ 在变换后的样子。
所以：
- $ B $ 是一个变换，它把空间“拉伸/旋转/压缩”成新的形状；
- $ A $ 接着又对这个已经变形的空间进行变换。
例：
$$
A = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}
$$
- $ B $ 的列是：
- $ \begin{bmatrix} 1 \\ 1 \end{bmatrix} $ → 第一个标准基向量变形后的位置
- $ \begin{bmatrix} -1 \\ 1 \end{bmatrix} $ → 第二个标准基向量变形后的位置
我们计算：
- $ A \cdot \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} $
- $ A \cdot \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix} $
所以：
$$
AB = \begin{bmatrix} 2 & -2 \\ 3 & 3 \end{bmatrix}
$$
这个新矩阵 $ AB $ 的列向量，表示标准基向量在经历了 **“先 B 再 A”** 的变换后，落在了哪里。
### 行列式
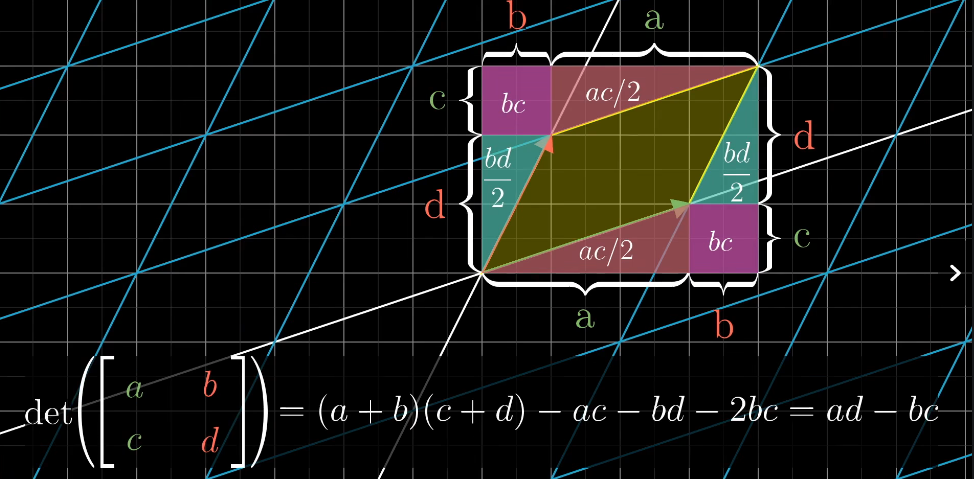
3blue1brown讲解行列式时，核心在于用几何直观来理解行列式的意义：
缩放比例！！！
**体积（或面积）的伸缩因子**
对于二维空间中的2×2矩阵，行列式的绝对值表示该矩阵作为线性变换时，对**单位正方形**施加变换后得到的平行四边形的面积。类似地，对于三维空间中的3×3矩阵，行列式的绝对值就是单位立方体变换后的平行六面体的体积。也就是说，行列式告诉我们这个变换如何“拉伸”或“压缩”空间。
**方向的指示（有向面积或体积）**
行列式不仅仅给出伸缩倍数，还通过正负号反映了变换是否保持了原来的方向（正）还是发生了翻转（负）。例如，在二维中，如果行列式为负，说明变换过程中存在翻转（类似镜像效果）。
**变换的可逆性**
当行列式为零时，说明该线性变换把空间**压缩到了低维**（例如二维变一条线，三维变成一个平面或线），这意味着信息在变换过程中丢失，变换不可逆。
![image-20250323104603200](https://pic.bitday.top/i/2025/03/23/j1llgr-0.png)
### 逆矩阵、列空间、零空间
#### **逆矩阵**
逆矩阵描述了一个矩阵所代表的线性变换的**“反过程”**。假设矩阵 $A$ 对空间做了某种变换（比如旋转、拉伸或压缩），那么 $A^{-1}$ 就是把这个变换“逆转”，把变换后的向量再映射回原来的位置。
前提是$A$ 是可逆的，即它对应的变换不会把空间压缩到更低的维度。
#### 秩
秩等于矩阵列向量（或行向量）**所生成的空间的维数**。例如，在二维中，如果一个 $2 \times 2$ 矩阵的秩是 2，说明这个变换把平面“充满”；如果秩为 1，则所有输出都落在一条直线上，说明变换“丢失”了一个维度。
#### 列空间
列空间是矩阵所有列向量的线性组合所构成的集合（也可以说所有可能的**输出向量**$A\mathbf{x}$所构成的集合）。 比如一个二维变换的列空间可能是整个平面，也可能只是一条直线，这取决于矩阵的秩。
#### 零空间
零空间（又称核、kernel）是所有在该矩阵作用（线性变换$A$）下变成零向量的**输入向量**的集合。
它展示了变换中哪些方向被“压缩”成了一个点（原点）。例如，在三维中，如果一个矩阵将所有向量沿某个方向压缩到零，那么这个方向构成了零空间。
零空间解释了$Ax=0$的解的集合，就是齐次的通解。如果满秩，零空间只有唯一解零向量。
#### 求解线性方程
设线性方程组写作
$$
A\mathbf{x} = \mathbf{b}
$$
这相当于在问：“有没有一个向量 $\mathbf{x}$ ，它经过矩阵 $A$ 的变换后，恰好落在 $\mathbf{b}$ 所在的位置？”
- 如果 $\mathbf{b}$ 落在 $A$ 的列空间内，那么就存在解。解可能是唯一的（当矩阵满秩时）或无穷多（当零空间非平凡时）。
- 如果 $\mathbf{b}$ 不在列空间内，则说明 $\mathbf{b}$ 不可能由 $A$ 的列向量线性组合得到，这时方程组无解。
- 唯一解对应于所有这些几何对象在一点相交；
- 无限多解对应于它们沿着某个方向重合；
- 无解则说明这些对象根本没有公共交点。
### 点积、哈达马积
**向量点积（Dot Product）**
3blue1brown认为，两个向量的点乘就是将其中一个向量转为线性变换。
假设有两个向量
$$
\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}.
$$
$$
\mathbf{v} \cdot \mathbf{w} =\begin{bmatrix} v_1 & v_2 \end{bmatrix}\begin{bmatrix} w_1 \\ w_2 \end{bmatrix}=v_1w_1 + v_2w_2..
$$
- **结果**：
点积的结果是一个**标量**（即一个数）。
- **几何意义**：
点积可以衡量两个向量的相似性，或者计算一个向量在另一个向量方向上的投影。
**哈达马积（Hadamard Product）**
- **定义**：
对于两个向量 $\mathbf{u} = [u_1, u_2, \dots, u_n]$ 和 $\mathbf{v} = [v_1, v_2, \dots, v_n]$，它们的哈达马积定义为：
$$
\mathbf{u} \circ \mathbf{v} = [u_1 v_1, u_2 v_2, \dots, u_n v_n].
$$
- **结果**：
哈达马积的结果是一个**向量**，其每个分量是对应位置的分量相乘。
- **几何意义**：
哈达马积通常用于逐元素操作，比如在神经网络中对两个向量进行逐元素相乘。
矩阵也有哈达马积！。
### 特征值和特征向量
设矩阵：
$$
A = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}
$$
步骤 1：求特征值
构造特征方程：
$$
\det(A - \lambda I) = \det\begin{bmatrix} 2-\lambda & 1 \\ 0 & 3-\lambda \end{bmatrix} = (2-\lambda)(3-\lambda) - 0 = 0
$$
解得：
$$
(2-\lambda)(3-\lambda) = 0 \quad \Longrightarrow \quad \lambda_1 = 2,\quad \lambda_2 = 3
$$
步骤 2：求特征向量
- 对于 $\lambda_1 = 2$：
解方程：
$$
(A - 2I)\mathbf{x} = \begin{bmatrix} 2-2 & 1 \\ 0 & 3-2 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_2 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
$$
从第一行 $x_2 = 0$。因此特征向量可以写成：
$$
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad (\text{任意非零常数倍})
$$
- 对于 $\lambda_2 = 3$：
解方程：
$$
(A - 3I)\mathbf{x} = \begin{bmatrix} 2-3 & 1 \\ 0 & 3-3 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -x_1+x_2 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
$$
从第一行得 $-x_1 + x_2 = 0$ 或 $x_2 = x_1$。因此特征向量可以写成：
$$
\mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \quad (\text{任意非零常数倍})
$$
**设一个对角矩阵**：
$$
D = \begin{bmatrix} d_1 & 0 \\ 0 & d_2 \end{bmatrix}
$$
$$
\lambda_1 = d_1,\quad \lambda_2 = d_2
$$
对角矩阵的特征方程为：
$$
\det(D - \lambda I) = (d_1 - \lambda)(d_2 - \lambda) = 0
$$
因此特征值是：
$$
\lambda_1 = d_1,\quad \lambda_2 = d_2
$$
- 对于 $\lambda_1 = d_1$，方程 $(D-d_1I)\mathbf{x}=\mathbf{0}$ 得到：
$$
\begin{bmatrix} 0 & 0 \\ 0 & d_2-d_1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ (d_2-d_1)x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
$$
若 $d_1 \neq d_2$，则必须有 $x_2=0$，而 $x_1$ 可任意取非零值，因此特征向量为：
$$
\mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}
$$
- 对于 $\lambda_2 = d_2$，类似地解得：
$$
\mathbf{v}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}
$$
### 矩阵乘法
**全连接神经网络**
![image-20250316145729703](https://pic.bitday.top/i/2025/03/23/j1lnso-0.png)
其中：
- $a^{(0)}$ 是输入向量，表示当前**层**的输入。
- $\mathbf{W}$ 是权重矩阵，表示输入向量到输出向量的线性变换。
- $b$ 是偏置向量，用于调整输出。
- $\sigma$ 是激活函数（如 ReLU、Sigmoid 等），用于引入非线性。
- **输入向量 $a^{(0)}$**：
$$
a^{(0)} = \begin{pmatrix}
a_0^{(0)} \\
a_1^{(0)} \\
\vdots \\
a_n^{(0)}
\end{pmatrix}
$$
这是一个 $n+1$ 维的列向量，表示输入特征。
- **权重矩阵 $\mathbf{W}$**：
$$
\mathbf{W} = \begin{pmatrix}
w_{0,0} & w_{0,1} & \cdots & w_{0,n} \\
w_{1,0} & w_{1,1} & \cdots & w_{1,n} \\
\vdots & \vdots & \ddots & \vdots \\
w_{k,0} & w_{k,1} & \cdots & w_{k,n} \\
\end{pmatrix}
$$
这是一个 $k \times (n+1)$ 的矩阵，其中 $k$ 是输出向量的维度，$n+1$ 是输入向量的维度。
- **偏置向量 $b$**：
$$
b = \begin{pmatrix}
b_0 \\
b_1 \\
\vdots \\
b_k
\end{pmatrix}
$$
这是一个 $k$ 维的列向量，用于调整输出。
1. 在传统的连续时间 RNN 写法里，常见的是
$$
\sum_{j} W_{ij} \, \sigma(x_j),
$$
这代表对所有神经元 $j$ 的激活 $\sigma(x_j)$ 做加权求和，再求和到神经元 $i$。
如果拆开来看，每个输出分量也都含一个求和 $\sum_{j}$：
- 输出向量的第 1 个分量（记作第 1 行的结果）：
$$
(W_r x)_1 = 0.3 \cdot x_1 + (-0.5) \cdot x_2 = 0.3 \cdot 2 + (-0.5) \cdot 1 = 0.6 - 0.5 = 0.1.
$$
- 输出向量的第 2 个分量（第 2 行的结果）：
$$
(W_r x)_2 = 1.2 \cdot x_1 + 0.4 \cdot x_2 = 1.2 \cdot 2 + 0.4 \cdot 1 = 2.4 + 0.4 = 2.8.
$$
2. 在使用矩阵乘法时，你可以写成
$$
y = W_r \, \sigma(x),
$$
其中 $\sigma$ 表示对 $x$ 的各分量先做激活，接着用 $W_r$ 乘上去。这就是把“$\sum_j \dots$”用矩阵乘法隐藏了。
$$
\begin{pmatrix}
0.3 & -0.5\\
1.2 & \;\,0.4
\end{pmatrix}
\begin{pmatrix}
2\\
1
\end{pmatrix}
=
\begin{pmatrix}
0.3 \times 2 + (-0.5) \times 1\\[6pt]
1.2 \times 2 + 0.4 \times 1
\end{pmatrix}
=
\begin{pmatrix}
0.6 - 0.5\\
2.4 + 0.4
\end{pmatrix}
=
\begin{pmatrix}
0.1\\
2.8
\end{pmatrix}.
$$
### 奇异值
**定义**
对于一个 $m \times n$ 的矩阵 $A$，其奇异值是非负实数 $\sigma_1, \sigma_2, \ldots, \sigma_r$（$r = \min(m, n)$），满足存在正交矩阵 $U$ 和 $V$，使得：
$$
A = U \Sigma V^T
$$
其中，$\Sigma$ 是对角矩阵，对角线上的元素即为奇异值。
---
**主要特点**
1. **非负性**：奇异值总是非负的。
2. 对角矩阵的奇异值是对角线元素的**绝对值**。
3. **降序排列**：通常按从大到小排列，即 $\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_r \geq 0$。
4. **矩阵分解**：奇异值分解（SVD）将矩阵分解为三个矩阵的乘积，$U$ 和 $V$ 是正交矩阵，$\Sigma$ 是对角矩阵。
5. **应用广泛**：奇异值在数据降维、噪声过滤、图像压缩等领域有广泛应用。
---
**计算**
奇异值可以通过计算矩阵 $A^T A$ 或 $A A^T$ 的特征值的**平方根**得到。
**步骤 1：计算 $A^T A$**
首先，我们计算矩阵 $A$ 的转置 $A^T$：
$$
A^T = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix}
$$
然后，计算 $A^T A$：
$$
A^T A = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} = \begin{pmatrix} 9 & 0 \\ 0 & 16 \end{pmatrix}
$$
**步骤 2：计算 $A^T A$ 的特征值**
接下来，我们计算 $A^T A$ 的特征值。特征值 $\lambda$ 满足以下特征方程：
$$
\det(A^T A - \lambda I) = 0
$$
即：
$$
\det \begin{pmatrix} 9 - \lambda & 0 \\ 0 & 16 - \lambda \end{pmatrix} = (9 - \lambda)(16 - \lambda) = 0
$$
解这个方程，我们得到两个特征值：
$$
\lambda_1 = 16, \quad \lambda_2 = 9
$$
**步骤 3：计算奇异值**
奇异值是特征值的平方根，因此我们计算：
$$
\sigma_1 = \sqrt{\lambda_1} = \sqrt{16} = 4
$$
$$
\sigma_2 = \sqrt{\lambda_2} = \sqrt{9} = 3
$$
**结果**
矩阵 $A$ 的奇异值为 **4** 和 **3**。
### 矩阵的迹
**迹的定义**
对于一个 $n \times n$ 的矩阵 $B$，其迹（trace）定义为矩阵对角线元素之和：
$$
\text{tr}(B) = \sum_{i=1}^n B_{ii}
$$
**迹与特征值的关系**
对于一个 $n \times n$ 的矩阵 $B$，其迹等于其特征值之和。即：
$$
\text{tr}(B) = \sum_{i=1}^n \lambda_i
$$
其中 $\lambda_1, \lambda_2, \ldots, \lambda_n$ 是矩阵 $B$ 的特征值。
**应用到 $A^* A$**
对于矩阵 $A^* A$（如果 $A$ 是实矩阵，则 $A^* = A^T$），它是一个半正定矩阵，其特征值是非负实数。
$A^* A$ 的迹还与矩阵 $A$ 的 Frobenius 范数有直接关系。具体来说：
$$
\|A\|_F^2 = \text{tr}(A^* A)
$$
**迹的基本性质**
迹是一个线性运算，即对于任意标量 $c_1, c_2$ 和矩阵 $A, B$，有：
$$
\text{tr}(c_1 A + c_2 B) = c_1 \text{tr}(A) + c_2 \text{tr}(B)
$$
对于任意矩阵 $A, B, C$，迹满足循环置换性质：
$$
\text{tr}(ABC) = \text{tr}(CAB) = \text{tr}(BCA)
$$
注意：迹的循环置换性**不**意味着 $\text{tr}(ABC) = \text{tr}(BAC)$，除非矩阵 $A, B, C$ 满足某些特殊条件（如对称性）。
### 酉矩阵
酉矩阵是一种复矩阵，其满足下面的条件：对于一个 $n \times n$ 的复矩阵 $U$，如果有
$$
U^* U = U U^* = I,
$$
其中 $U^*$ 表示 $U$ 的共轭转置（先转置再取复共轭），而 $I$ 是 $n \times n$ 的单位矩阵，那么 $U$ 就被称为酉矩阵。简单来说，酉矩阵在复内积空间中保持内积不变，相当于在该空间中的“旋转”或“反射”。
如果矩阵的元素都是实数，那么 $U^*$ 就等于 $U^T$（转置），这时酉矩阵就退化为**正交矩阵**。
考虑二维旋转矩阵
$$
U = \begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}.
$$
当 $\theta$ 为任意实数时，这个矩阵满足
$$
U^T U = I,
$$
所以它是一个正交矩阵，同时也属于酉矩阵的范畴。
例如，当 $\theta = \frac{\pi}{4}$（45°）时，
$$
U = \begin{bmatrix}
\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}
\end{bmatrix}.
$$
### 对称非负矩阵分解
$$
A≈HH^T
$$
**1. 问题回顾**
给定一个**对称非负**矩阵 $A\in\mathbb{R}^{n\times n}$，我们希望找到一个**非负矩阵** $H\in\mathbb{R}^{n\times k}$ 使得
$$
A \approx HH^T.
$$
为此，我们可以**最小化目标函数(损失函数)**
$$
f(H)=\frac{1}{2}\|A-HH^T\|_F^2,
$$
其中 $\|\cdot\|_F$ 表示 Frobenius 范数，定义为矩阵所有元素的平方和的平方根。
$\| A - H H^T \|_F^2$ 表示矩阵 $A - H H^T$ 的所有元素的平方和。
**2. 梯度下降方法**
2.1 计算梯度
目标函数(损失函数)是
$$
f(H)=\frac{1}{2}\|A-HH^T\|_F^2.
$$
$$
\|M\|_F^2 = \operatorname{trace}(M^T M),
$$
因此，目标函数可以写成：
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^T\bigl(A-HH^T\bigr)\Bigr].
$$
注意到 $A$ 和$HH^T$ 都是对称矩阵，可以简化为：
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^2\Bigr].
$$
展开后得到
$$
f(H)=\frac{1}{2}\operatorname{trace}\Bigl[A^2 - 2AHH^T + (HH^T)^2\Bigr].
$$
其中 $\operatorname{trace}(A^2)$ 与 $H$ 无关，可以看作常数，不影响梯度计算。
**计算** $\nabla_H \operatorname{trace}(-2 A H H^T)$
$$
\nabla_H \operatorname{trace}(-2 A H H^T) = -4 A H
$$
**计算** $\nabla_H \operatorname{trace}((H H^T)^2)$
$$
\nabla_H \operatorname{trace}((H H^T)^2) = 4 H H^T H
$$
将两部分梯度合并：
$$
\nabla_H f(H) = \frac{1}{2}(4 H H^T H - 4 A H )= 2(H H^T H - A H)
$$
2.2 梯度下降更新
设学习率为 $\eta>0$，则梯度下降的**基本更新公式为**：
$$
H \leftarrow H - \eta\, \nabla_H f(H) = H - 2\eta\Bigl(HH^T H - A H\Bigr).
$$
由于我们要求 $H$ 中的元素保持非负，所以每次更新之后通常需要进行**投影**：
$$
H_{ij} \leftarrow \max\{0,\,H_{ij}\}.
$$
这种方法称为**投影梯度下降**，保证每一步更新后 $H$ 满足非负约束。
**3. 举例说明**
设对称非负矩阵：
$$
A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}, \quad k=1, \quad H \in \mathbb{R}^{2 \times 1}
$$
初始化 $H^{(0)} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$，学习率 $\eta = 0.01$。
**迭代步骤**：
1. **初始 \( H^{(0)} \):**
$$
H^{(0)} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}, \quad H^{(0)}(H^{(0)})^T = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}.
$$
目标函数值：
$$
f(H^{(0)}) = \frac{1}{2} \left( (2-1)^2 + 2(1-1)^2 + (2-1)^2 \right) = 1.
$$
2. **计算梯度：**
$$
HH^T H = \begin{bmatrix} 2 \\ 2 \end{bmatrix}, \quad AH = \begin{bmatrix} 3 \\ 3 \end{bmatrix},
$$
$$
\nabla_H f(H^{(0)}) = 2 \left( \begin{bmatrix} 2 \\ 2 \end{bmatrix} - \begin{bmatrix} 3 \\ 3 \end{bmatrix} \right) = \begin{bmatrix} -2 \\ -2 \end{bmatrix}.
$$
3. **更新 \( H \):**
$$
H^{(1)} = H^{(0)} - 2 \cdot 0.01 \cdot \begin{bmatrix} -2 \\ -2 \end{bmatrix} = \begin{bmatrix} 1.04 \\ 1.04 \end{bmatrix}.
$$
4. **更新后目标函数：**
$$
H^{(1)}(H^{(1)})^T = \begin{bmatrix} 1.0816 & 1.0816 \\ 1.0816 & 1.0816 \end{bmatrix},
$$
$$
f(H^{(1)}) = \frac{1}{2} \left( (2-1.0816)^2 + 2(1-1.0816)^2 + (2-1.0816)^2 \right) \approx 0.8464.
$$
一次迭代后目标函数值从 $1.0$ 下降至 $0.8464$

190
科研/草稿.md
View File

@ -1,7 +1,187 @@
对于传统的 transductive GCN 模型来说，公式中的 $\tilde{A}$（包含自环的邻接矩阵）和 $\tilde{D}$（其对应的度矩阵）的大小通常是基于训练时整个图的结构，是固定的。 ---
## 该部分主要内容概述
在这部分（论文 2.1 节 “Graph Attentional Layer”）中，作者提出了图注意力网络（GAT）中最核心的运算：**图注意力层**。它的基本思想是：
1. **线性变换**：先对每个节点的特征 $\mathbf{h}_i$ 乘上一个可学习的权重矩阵 $W$，得到变换后的特征 $W \mathbf{h}_i$。
2. **自注意力机制**：通过一个可学习的函数 $a$，对节点 $i$ 和其邻居节点 $j$ 的特征进行计算，得到注意力系数 $e_{ij}$。这里会对邻居进行遮蔽（masked attention），即只计算图中有边连接的节点对。
3. **归一化**：将注意力系数 $e_{ij}$ 通过 softmax 进行归一化，得到 $\alpha_{ij}$，表示节点 $j$ 对节点 $i$ 的重要性权重。
4. **聚合**：最后利用注意力系数加权邻居节点的特征向量，并经过激活函数得到新的节点表示 $\mathbf{h}_i'$。
5. **多头注意力**：为增强表示能力，可并行地执行多个独立的注意力头（multi-head attention），再将它们的结果进行拼接（或在最后一层进行平均），从而得到最终的节点表示。
该部分给出的公式主要包括注意力系数的计算、softmax 归一化、多头注意力的聚合方式等，下面逐一用 Markdown 数学公式的形式列出。
---
## 公式列表（Markdown 格式）
> **注意**：以下公式与论文中编号对应（如 (1)、(2)、(3)、(4)、(5)、(6) 等）。
1. **注意力系数（未归一化）**
$$
e_{ij} = a\bigl(W\mathbf{h}_i,\; W\mathbf{h}_j\bigr)
$$
2. **注意力系数的 softmax 归一化**
$$
\alpha_{ij} = \text{softmax}_j\bigl(e_{ij}\bigr)
= \frac{\exp\bigl(e_{ij}\bigr)}{\sum_{k \in \mathcal{N}_i} \exp\bigl(e_{ik}\bigr)}
$$
​ $\alpha_{ij}$表示节点 $i$ 对节点 $j$ 的注意力权重
3. **具体的注意力计算形式（以单层前馈网络 + LeakyReLU 为例）**
$$
\alpha_{ij}
= \frac{\exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_j\bigr]\bigr)\Bigr)}
{\sum_{k\in \mathcal{N}_i} \exp\Bigl(\text{LeakyReLU}\bigl(\mathbf{a}^\top \bigl[\;W\mathbf{h}_i \,\|\, W\mathbf{h}_k\bigr]\bigr)\Bigr)}
$$
其中，$\mathbf{a}$ 为可学习的参数向量，$\|$ 表示向量拼接（concatenation）。
4. **单头注意力聚合（得到新的节点特征）**
$$
\mathbf{h}_i' = \sigma\Bigl(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \,W \mathbf{h}_j\Bigr)
$$
其中，$\sigma$ 表示非线性激活函数（如 ELU、ReLU 等），$\mathcal{N}_i$ 表示节点 $i$ 的邻居节点集合（可包含 $i$ 自身）。
5. **多头注意力（隐藏层时拼接）**
如果有 $K$ 个独立的注意力头，每个头输出 $\mathbf{h}_i'^{(k)}$，则拼接后的输出为：
$$
\mathbf{h}_i' =
\big\Vert_{k=1}^K
\sigma\Bigl(\sum_{j \in \mathcal{N}_i} \alpha_{ij}^{(k)} \, W^{(k)} \mathbf{h}_j\Bigr)
$$
其中，$\big\Vert$ 表示向量拼接操作，$\alpha_{ij}^{(k)}$、$W^{(k)}$ 分别为第 $k$ 个注意力头对应的注意力系数和线性变换。
6. **多头注意力（输出层时平均）**
在最终的输出层（例如分类层）通常会将多个头的结果做平均，而不是拼接：
$$
\mathbf{h}_i' =
\sigma\Bigl(
\frac{1}{K} \sum_{k=1}^K \sum_{j \in \mathcal{N}_i}
\alpha_{ij}^{(k)} \, W^{(k)} \mathbf{h}_j
\Bigr)
$$
---
以上即是论文中 2.1 节（Graph Attentional Layer）出现的主要公式及其简要说明。
### 2. **GAT 的聚合方式**
- **GAT** 使用了一种**自适应的、可学习的注意力机制**来聚合节点及其邻居的信息。
- 具体来说，GAT 的聚合公式为：
$$
h_i^{(l+1)} = \sigma\left(\sum_{j \in \mathcal{N}(i) \cup \{i\}} \alpha_{ij} W h_j^{(l)}\right)
$$
其中：
- $\alpha_{ij}$ 是节点 $i$ 和节点 $j$ 之间的**注意力系数**，通过以下方式计算：
$$
\alpha_{ij} = \frac{\exp(\text{LeakyReLU}(a^T [W h_i \| W h_j]))}{\sum_{k \in \mathcal{N}(i) \cup \{i\}} \exp(\text{LeakyReLU}(a^T [W h_i \| W h_k]))}
$$
- $a$ 是一个可学习的注意力向量。
- $\|$ 表示特征拼接操作。
- $W$ 是可学习的权重矩阵。
- $\sigma$ 是非线性激活函数。
- **特点**：
- GAT 的聚合权重是**动态的**，通过注意力机制学习得到。
- 权重是非对称的，且可以捕捉节点之间的复杂关系。
- 相当于对节点及其邻居进行了一种**加权信息传递**，权重由数据驱动。
---
### 3. **GCN 和 GAT 的对比**
| 特性 | GCN | GAT |
| ------------------ | ------------------------ | -------------------------- |
| **聚合方式** | 固定的加权平均 | 自适应的注意力加权 |
| **权重是否可学习** | 否（权重由节点度数决定） | 是（通过注意力机制学习） |
| **权重是否对称** | 是 | 否 |
| **表达能力** | 较弱（固定的聚合方式） | 较强（动态的聚合方式） |
| **计算复杂度** | 较低 | 较高（需要计算注意力系数） |
| **适用场景** | 简单的图结构任务 | 复杂的图结构任务 |
---
### 4. **直观理解**
- **GCN**：
- 类似于对邻居节点进行“民主投票”，每个邻居的权重是固定的（由度数决定）。
- 适合处理节点度数分布均匀、关系相对简单的图。
- **GAT**：
- 类似于对邻居节点进行“加权投票”，每个邻居的权重是动态学习的。
- 适合处理节点度数分布不均匀、关系复杂的图。
---
### 5. **总结**
- **GCN** 使用的是**固定的、归一化的加权平均**，权重由节点度数决定。
- **GAT** 使用的是**自适应的、可学习的注意力权重**，权重通过数据驱动的方式学习得到。
- GAT 的表达能力更强，但计算复杂度也更高；GCN 更简单高效，但表达能力相对较弱。
希望这个解释能帮助你更好地理解 GCN 和 GAT 的区别！如果还有疑问，欢迎继续讨论！
3blue1brown 的讲解试图让我们从几何和线性映射的角度来理解点乘，而不仅仅是将它看作一系列数的乘加运算。下面详细说明这一点。
假设有两个向量
$$
\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}.
$$
传统上，点乘定义为
$$
\mathbf{v} \cdot \mathbf{w} = v_1w_1 + v_2w_2.
$$
3blue1brown 的观点是：
- **将一个向量视为线性变换**
我们可以把 $\mathbf{v}$ 当作一个线性映射，它把任何向量 $\mathbf{w}$ 映射为一个实数，即
$$
T_{\mathbf{v}}(\mathbf{w}) = \mathbf{v}\cdot \mathbf{w}.
$$
这个映射 $T_{\mathbf{v}}$ 是一个**线性泛函**，它具有线性性：
$$
T_{\mathbf{v}}(a\mathbf{w}_1 + b\mathbf{w}_2) = aT_{\mathbf{v}}(\mathbf{w}_1) + bT_{\mathbf{v}}(\mathbf{w}_2).
$$
换句话说，$\mathbf{v}$ 变成了一个“工具”，通过这个工具我们可以“测量”任一向量在 $\mathbf{v}$ 方向上的分量大小。
- **几何直观**
如果我们记 $\theta$ 为 $\mathbf{v}$ 和 $\mathbf{w}$ 之间的夹角，则点乘也可以写作
$$
\mathbf{v} \cdot \mathbf{w} = \|\mathbf{v}\|\|\mathbf{w}\|\cos\theta.
$$
这里，$\|\mathbf{w}\|\cos\theta$ 就是 $\mathbf{w}$ 在 $\mathbf{v}$ 方向上的投影长度。当我们用 $\|\mathbf{v}\|$ 乘上这个投影长度时，就得到了一个度量，这个度量告诉我们 $\mathbf{w}$ 在 $\mathbf{v}$ 方向上“有多大”的贡献。
- **矩阵乘法的视角**
我们也可以把点乘看作行向量和列向量的矩阵乘法：
$$
\mathbf{v}\cdot \mathbf{w} = \begin{bmatrix} v_1 & v_2 \end{bmatrix}\begin{bmatrix} w_1 \\ w_2 \end{bmatrix}.
$$
在这个表达式中，$\begin{bmatrix} v_1 & v_2 \end{bmatrix}$ 就相当于一个将二维向量映射到实数的线性变换，也正是我们上面定义的 $T_{\mathbf{v}}(\cdot)$。
总结来说，3blue1brown 强调的点乘本质是：
- 把固定的向量 $\mathbf{v}$ 转换成一个线性映射（或线性泛函），这个映射作用在任意向量 $\mathbf{w}$ 上，返回一个标量；
- 这个标量不仅包含了 $\mathbf{w}$ 在 $\mathbf{v}$ 方向上的“投影”信息，而且反映了两者之间的对齐程度（通过余弦函数体现）；
- 因此，点乘不仅仅是数值运算，而是一个把向量转换成测量工具，从而揭示向量间角度和方向关系的过程。
然而，在归纳式设置下（例如在 GraphSAGE 或一些扩展的 GCN 模型中），当有新节点加入时，你可以构造一个包含新节点及其局部邻居的子图，然后重新计算该局部子图的 $\tilde{A}$ 和 $\tilde{D}$ 矩阵。这样就不需要对整个图做全局归一化，而是只关注新节点及其相关邻居的局部结构，从而生成新节点的表示。
**简洁总结：**
- **固定图（Transductive）**：$\tilde{A}$ 和 $\tilde{D}$ 大小固定，因为它们对应整个图。
- **归纳式方法**：对于新节点，可以基于新节点和其选定的邻居构造局部子图，重新计算局部的 $\tilde{A}$ 和 $\tilde{D}$，从而实现在线生成表示。