diff --git a/后端学习/JAVA面试题.md b/后端学习/JAVA面试题.md index c4f508e..4d01b6b 100644 --- a/后端学习/JAVA面试题.md +++ b/后端学习/JAVA面试题.md @@ -90,3 +90,51 @@ if (V == A) { } ``` + + +如何多线程循环打印1-100数字？ + +```java +public class AlternatePrint { + private static int count = 1; + private static final Object lock = new Object(); + + public static void main(String[] args) { + new Thread(() -> { + while (count <= 100) { + synchronized (lock) { + if (count % 2 == 1) { + System.out.println(Thread.currentThread().getName() + ": " + count++); + lock.notify(); + } else { + try { + lock.wait(); + } catch (InterruptedException e) { + e.printStackTrace(); + } + } + } + } + }, "Thread-1").start(); + + new Thread(() -> { + while (count <= 100) { + synchronized (lock) { + if (count % 2 == 0) { + System.out.println(Thread.currentThread().getName() + ": " + count++); + lock.notify(); + } else { + try { + lock.wait(); + } catch (InterruptedException e) { + e.printStackTrace(); + } + } + } + } + }, "Thread-2").start(); + } +} + +``` + diff --git a/后端学习/力扣Hot 100题.md b/后端学习/力扣Hot 100题.md index b199544..7a4971e 100644 --- a/后端学习/力扣Hot 100题.md +++ b/后端学习/力扣Hot 100题.md @@ -183,6 +183,8 @@ public class RandomDemo { 子序列：字符串中**按顺序选取的一段字符**，可以不连续。 +子数组：等于连续子序列 + 异位词：字母相同、字母频率相同、顺序不同，如`"listen"` 和 `"silent"` @@ -1175,6 +1177,22 @@ public class QuickSort { +**Java随机** + +```java +mport java.util.Random; + +public class RandomDemo { + public static void main(String[] args) { + Random random = new Random(); + int num = random.nextInt(6); // 生成 [0, 5] 的随机整数 + System.out.println(num); + } +} +``` + + + ### 快速选择 时间复杂度: O(n) @@ -1183,58 +1201,53 @@ public class QuickSort { public class QuickSelect { /** - * 在 nums[low..high] 区间内，寻找排序后下标为 k 的元素（第 k 小） + * 对 arr 在 [low..high] 范围内，使用“挖坑填坑”分区，返回枢轴的最终位置 */ - public int quickselect(int[] nums, int low, int high, int k) { - // 区间内只有一个元素，直接返回 - if (low == high) { - return nums[low]; - } - - // 选取区间第一个元素作为枢轴 - int pivot = nums[low]; + private int partition(int[] arr, int low, int high) { + int pivot = arr[low]; int left = low, right = high; - - // “挖坑填坑”分区：左边填小于 pivot 的值，右边填大于 pivot 的值 while (left < right) { - // 从右向左找第一个 < pivot 的 - while (left < right && nums[right] >= pivot) { + while (left < right && arr[right] >= pivot) { right--; } - nums[left] = nums[right]; // 填到左“坑” - - // 从左向右找第一个 > pivot 的 - while (left < right && nums[left] <= pivot) { + arr[left] = arr[right]; + while (left < right && arr[left] <= pivot) { left++; } - nums[right] = nums[left]; // 填到右“坑” - } - - // 把 pivot 放回最终位置 - nums[left] = pivot; - - // 根据 pivot 位置与 k 比较，决定去哪一边继续 - if (left == k) { - return nums[left]; - } else if (k < left) { - return quickselect(nums, low, left - 1, k); - } else { - return quickselect(nums, left + 1, high, k); + arr[right] = arr[left]; } + arr[left] = pivot; + return left; } /** - * 返回数组中第 k 大的元素 - * @param nums 输入数组 - * @param k 1-based，第 k 大 + * 在 arr[low..high] 区间内，寻找第 k 小元素（k 从 0 开始） + */ + public int quickselect(int[] arr, int low, int high, int k) { + if (low <= high) { + int pivotPos = partition(arr, low, high); + if (pivotPos == k) { + return arr[pivotPos]; + } else if (k < pivotPos) { + return quickselect(arr, low, pivotPos - 1, k); + } else { + return quickselect(arr, pivotPos + 1, high, k); + } + } + // 理论上不会走到这里，除非 k 越界 + throw new IllegalArgumentException("k is out of bounds"); + } + + /** + * 返回数组中第 k 大的元素（k 从 1 开始） */ public int findKthLargest(int[] nums, int k) { int n = nums.length; - // 第 k 大对应第 (n - k) 小 + // 第 k 大就是第 (n - k) 小 return quickselect(nums, 0, n - 1, n - k); } - } + ``` diff --git a/科研/草稿.md b/科研/草稿.md index cd2ea1e..31047b9 100644 --- a/科研/草稿.md +++ b/科研/草稿.md @@ -1,79 +1,103 @@ -### 收缩矩阵的逐次特征值提取方法 -#### 1. 初始矩阵性质 -对于实对称矩阵 $A \in \mathbb{R}^{N \times N}$，当满足： -- 非对角元素 $a_{ij}$ 独立同分布 -- 均值 $\mathbb{E}[a_{ij}] = \mu$ -- 方差 $\text{Var}(a_{ij}) = \sigma^2$ -- 对角元素 $a_{ii} = 0$ -其最大特征值 $\lambda_1$ 服从高斯分布： +### 定理2 +多智能体随机网络矩阵奇异值信号系统具有线性特征。 + +#### 证明 +根据定理1，奇异值序列$\sigma_{\tilde{\kappa}}(A_t)$服从高斯分布$\mathcal{N}(m_{\tilde{\kappa}}, 2\sigma_{\tilde{\kappa}}^2)$，其协方差结构满足： $$ -\mathbb{E}[\lambda_1] (N-1)\mu + \frac{\sigma^2}{\mu}, \quad \text{Var}(\lambda_1) = 2\sigma^2 +\gamma_{\tilde{\kappa}}(h) = 2\sigma_{\tilde{\kappa}}^2\delta_h^0 $$ -#### 2. 收缩操作定义 -通过秩一修正实现矩阵收缩： +定义中心化变量： $$ -A^{(k+1)} = A^{(k)} - \lambda_k u_k u_k^T +\tilde{\sigma}_t = \sigma_{\tilde{\kappa}}(A_t) - m_{\tilde{\kappa}} +$$ +可表示为： +$$ +\tilde{\sigma}_t = \sqrt{2}\sigma_{\tilde{\kappa}}\varepsilon_t, \quad \varepsilon_t \overset{i.i.d.}{\sim} \mathcal{N}(0,1) +$$ + +#### 线性系统验证 +该系统为MA(0)过程，系统增益$h_0 = \sqrt{2}\sigma_{\tilde{\kappa}}$，满足： +1. **齐次性**： + $$a\tilde{\sigma}_t = h_0(a\varepsilon_t)$$ +2. **叠加性**： + $$\tilde{\sigma}_t^{(1)} + \tilde{\sigma}_t^{(2)} = h_0(\varepsilon_t^{(1)} + \varepsilon_t^{(2)})$$ + +#### 结论 +奇异值序列的完整表示： +$$ +\sigma_{\tilde{\kappa}}(A_t) = m_{\tilde{\kappa}} + h_0\varepsilon_t $$ 其中： -- $\lambda_k$ 为当前矩阵 $A^{(k)}$ 的最大特征值 -- $u_k$ 为对应特征向量（单位范数） -- 初始条件 $A^{(1)} = A$ +- $m_{\tilde{\kappa}}$为稳态偏置项 +- $h_0\varepsilon_t$为线性系统响应 -#### 3. 特征值递推关系 -第 $k$ 大特征值可通过收缩矩阵提取： +根据线性系统定义（需引用文献），同时满足齐次性与可加性即构成线性系统，故得证。 + + + + + + + + + + + + + + + +--- + +### ② 定理2修订（线性系统特征） + +#### 原MA(0)情形回顾 + +当$\gamma_k(h)=2\sigma_k^2\delta_h$时， $$ -\lambda_k(A) = \lambda_1(A^{(k)}) +\tilde{\sigma}_t=\sigma_k(A_t)-m_k=\sqrt{2}\sigma_k\varepsilon_t, \quad \varepsilon_t \overset{i.i.d.}{\sim} \mathcal{N}(0,1) $$ -若收缩后矩阵 $A^{(k)}$ 保持： -- 非对角元素均值 $\mu_k$ -- 方差 $\sigma_k^2$ +#### 新协方差结构下的表示 -则特征值统计量满足： +当$\gamma_k(h)=C_h$（允许$C_h\neq0$），根据Wiener-Kolmogorov表示定理： $$ -\begin{cases} -\mathbb{E}[\lambda_k] = (N-k)\mu_k + \frac{\sigma_k^2}{\mu_k} \\ -\text{Var}(\lambda_k) = 2\sigma_k^2 -\end{cases} +\tilde{\sigma}_t=\sum_{h=-\infty}^{+\infty} b_h w_{t-h} \tag{1} +$$ +其中$\{b_h\}\in\ell^2$满足： +$$ +\gamma_k(h)=\sum_{\ell=-\infty}^{+\infty} b_\ell b_{\ell+h} \tag{2} $$ -#### 4. 实现步骤 -1. **初始化**：设 $A^{(1)} = A$，$k=1$ -2. **迭代过程**： - ```python - while k <= K: - # 计算当前最大特征对 - λ, u = eigsh(A^{(k)}, k=1) - - # 记录统计量 - λ_sequence[k] = λ - - # 执行收缩 - A^{(k+1)} = A^{(k)} - λ * u @ u.T - - # 验证新矩阵性质 - μ_k = np.mean(A^{(k+1)}[off_diag]) - σ²_k = np.var(A^{(k+1)}[off_diag]) - - k += 1 +#### 线性系统验证 -$\sigma_1$. +设系统传递函数$H(z)=\sum_h b_h z^{-h}$： +1. **齐次性** + $$ + a\tilde{\sigma}_t=a\sum_h b_h w_{t-h}=\sum_h b_h (a w_{t-h})=H(z)\{a w_t\} + $$ +2. **叠加性** + $$ + \tilde{\sigma}_t^{(1)}+\tilde{\sigma}_t^{(2)}=\sum_h b_h(w_{t-h}^{(1)}+w_{t-h}^{(2)})=H(z)\{w_t^{(1)}+w_t^{(2)}\} + $$ +故$\{\sigma_k(A_t)\}$仍是LTI系统输出，但系统响应$\{b_h\}$需通过(2)式确定。 +--- -您说得对，在奇异值分解(SVD)中，通常用 **u** 和 **v** 来表示左右奇异向量。以下是修正后的Markdown格式表示： +### 性质对比 -对于随机网络矩阵 `A`，设奇异值从大到小依次为 `{\sigma _1},{\sigma _2}, \ldots ,{\sigma _n}`，对应的左、右奇异向量分别为 ${u}_1, {u}_2, \ldots, {u}_n$ 和 ${v}_1, {v}_2, \ldots,{v}_n$。 - -或者更紧凑地表示为： - `A = \sum_{i=1}^n \sigma_i \mathbf{u}_i \mathbf{v}_i^\top` - -需要其他数学符号表示或格式调整可以随时告诉我！ +| 性质 | $\gamma_k(h)=2\sigma_k^2\delta_h$ | $\gamma_k(h)=C_h$ | +| -------- | --------------------------------- | -------------------------------- | +| 宽平稳 | ✅ | ✅ | +| 白噪声 | ✅ | ❌ | +| 系统类型 | MA(0) | 通用LTI（可能MA($\infty$)） | +| 谱密度 | $S(f)=2\sigma_k^2$ | $S(f)=\sum_h C_h e^{-j2\pi f h}$ | @@ -81,18 +105,126 @@ $\sigma_1$. -不必大动干戈，只要把“等号”换成“近似”等价写法，或显式加上误差项，就足够严谨。下面给出两种常见做法，你任选其一即可—— +### 随机网络稳态奇异值的平稳性证明 -| 写法 | 建议格式 | 说明 | -| -------------- | ------------------------------------------------------------ | ------------------------------------------------------------ | -| **近似号写法** | E[σ1]≈(N−1)μ+v+σ2μ,Var⁡[σ1]≈2σ2E[\sigma_1]\approx (N-1)\mu+v+\dfrac{\sigma^2}{\mu},\qquad \operatorname{Var}[\sigma_1]\approx 2\sigma^2 | 直接用 “≈” 表明这是 N→∞N\to\infty 的主导项；与前面“可在 O(1/N)O(1/\sqrt N) 范围内逼近高斯”完全呼应。 | -| **误差项写法** | E[σ1]=(N−1)μ+v+σ2μ+O ⁣(1N),Var⁡[σ1]=2σ2+O ⁣(1N)E[\sigma_1]=(N-1)\mu+v+\dfrac{\sigma^2}{\mu}+O\!\left(\tfrac{1}{N}\right),\qquad \operatorname{Var}[\sigma_1]=2\sigma^2+O\!\left(\tfrac{1}{N}\right) | 把小量显式写成 O(1/N)O(1/N)。这样保留等号，同时说明误差级别，更“硬核”一些。 | +#### 1. 稳态奇异值分布特性 -> **为什么推荐修改？** -> -> - 你的正文已经说“在 O(1/N)O(1/\sqrt N) 的范围内可被高斯分布逼近”，说明后续公式仅是渐近主项。直接用 “=” 容易让读者误以为 **完全等于** 主项。 -> - 只要在公式里加 “≈” 或 “+O(\cdot)” 就能避免歧义，而且和引用的 F & K 定理保持一致。 +当随机网络进入稳态后，其矩阵序列$\{A_t\}$的任意奇异值$\sigma_k(A_t)$服从高斯分布： +$$ +\sigma_k(A_t) \sim \mathcal{N}(m_k, \gamma_k(0)) +$$ +其中参数满足： -其余内容（条件、符号、文字描述）都没问题，不必再改。 +- **均值**：$m_k = (N-1)\mu_k + v_k + \frac{\sigma_k^2}{\mu_k}$ + （$N$为网络规模，$\mu_k,v_k,\sigma_k$为网络参数） +- **方差**：$\gamma_k(0) = 2\sigma_k^2$ -$\approx$ +#### 2. 宽平稳性验证 + +对任意时刻$t$： + +1. **均值稳定性**： + $$ + \mathbb{E}[\sigma_k(A_t)] = m_k \quad \text{(常数)} + $$ + +2. **协方差结构**： + + - 当$h=0$时： + $$ + \text{Cov}(\sigma_k(A_t), \sigma_k(A_t)) = \gamma_k(0) + $$ + + - 当$h \neq 0$时： + $$ + \text{Cov}(\sigma_k(A_t), \sigma_k(A_{t+h})) = \gamma_k(h)=0 + $$ + （由稳态下矩阵的独立性保证） + +#### 3. 结论 + +自协方差函数$\gamma_k(h)$仅依赖于时滞$h$，因此奇异值信号序列$\{\sigma_k(A_t)\}$满足宽平稳过程的定义。 + +--- + +**注**：本证明基于以下假设： + +1. 网络规模$N$足够大，使得高斯逼近有效 +2. 稳态下矩阵序列$\{A_t\}$具有独立性 + + + +### 定理2 +多智能体随机网络矩阵奇异值信号系统具有线性特征。 + +#### 证明 +根据定理1，奇异值序列$\sigma_{\tilde{\kappa}}(A_t)$服从高斯分布$\mathcal{N}(m_{\tilde{\kappa}}, 2\sigma_{\tilde{\kappa}}^2)$，其协方差结构满足： +$$ +\gamma_{\tilde{\kappa}}(h) = 2\sigma_{\tilde{\kappa}}^2\delta_h^0 +$$ + +定义中心化变量： +$$ +\tilde{\sigma}_t = \sigma_{\tilde{\kappa}}(A_t) - m_{\tilde{\kappa}} +$$ +可表示为： +$$ +\tilde{\sigma}_t = \sqrt{2}\sigma_{\tilde{\kappa}}\varepsilon_t, \quad \varepsilon_t \overset{i.i.d.}{\sim} \mathcal{N}(0,1) +$$ + +#### 线性系统验证 +该系统为MA(0)过程，系统增益$h_0 = \sqrt{2}\sigma_{\tilde{\kappa}}$，满足： +1. **齐次性**： + $$a\tilde{\sigma}_t = h_0(a\varepsilon_t)$$ +2. **叠加性**： + $$\tilde{\sigma}_t^{(1)} + \tilde{\sigma}_t^{(2)} = h_0(\varepsilon_t^{(1)} + \varepsilon_t^{(2)})$$ + +#### 结论 +奇异值序列的完整表示： +$$ +\sigma_{\tilde{\kappa}}(A_t) = m_{\tilde{\kappa}} + h_0\varepsilon_t +$$ +其中： +- $m_{\tilde{\kappa}}$为稳态偏置项 +- $h_0\varepsilon_t$为线性系统响应 + +根据线性系统定义（需引用文献），同时满足齐次性与可加性即构成线性系统，故得证。 + + + + + + + + + + + + + + + +……由协方差结构 γ_k(h)=2σ_k^2δ_h^0 可知，中心化变量 +$$ +\tilde σ_t = σ_k(A_t)-m_k,\qquad +\mathbb E[\tilde σ_t]=0,\; \mathrm{Cov}(\tilde σ_t,\tilde σ_{t+h})= +2σ_k^{2}\delta_h^{0}. +$$ + +**根据 Wold 分解定理①**，任何零均值、纯非确定性的宽平稳过程都可以唯一表示为 + +$$ +\tilde σ_t=\sum_{j=0}^{\infty}ψ_j\;ε_{t-j}, +\qquad ε_t\stackrel{i.i.d.}{\sim}\mathcal N(0,1),\ +\sum_{j=0}^{\infty}|ψ_j|^2<\infty. +$$ + +而在本情形下 $\gamma_k(h)=0\,(h\neq 0)$，因此 +$$ +ψ_0=\sqrt{2}\,σ_k,\quad ψ_j=0\;(j\ge 1), +$$ +退化为一个 **MA(0)** 过程： +$$ +\boxed{\;\tilde σ_t=\sqrt{2}\,σ_k\,ε_t\;} +$$ +…… diff --git a/论文/高飞论文.md b/论文/高飞论文.md index f80edad..251ff60 100644 --- a/论文/高飞论文.md +++ b/论文/高飞论文.md @@ -58,6 +58,10 @@ + + + + ### 证明主特征值序列平稳 #### **(1) 均值恒定性的推导** @@ -530,3 +534,9 @@ LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$（其中 $d''$ 为 LSTM 该论文可能有点问题，每个节点只能预测自身未来位置，无法获取全局位置信息。如果先LSTM后GCN可能可以！ + + + + + + diff --git a/项目/拼团交易系统.md b/项目/拼团交易系统.md index 0a79716..319d626 100644 --- a/项目/拼团交易系统.md +++ b/项目/拼团交易系统.md @@ -14,7 +14,11 @@ 用户锁单-》支付宝付款-》成功后return_url设置了用户支付完毕后跳转回哪个地址是给前端用户看的； alipay_notify_url设置了支付成功后alipay调用你的后端哪个接口。 -这里有小商城和拼团系统，notify_url指拼团系统中拼团达到指定人数后，通知小商城的地址，这里用rabbitmq。然后小商场将订单中相应拼团的status都设置为deal_done。然后小商场内部也再发一个'支付成功'消息，主要用于通知这些拼团对应的订单进入下一环节：发货（感觉'支付成功'取名不够直观）。 +这里有小商城和拼团系统，notify_url指拼团系统中拼团达到指定人数后，通知小商城的HTTP地址，但是如果notify_type为MQ，则notify_url为空，并且notify_mq非空，指明是拼团成功通知还是用户退单通知。 + +若为拼团成功通知，小商场将订单中相应拼团的status都设置为deal_done，然后小商场内部也再发一个'支付成功'消息，主要用于通知这些拼团对应的订单进入下一环节：发货（感觉'支付成功'取名不够直观）。 + +若为用户退单通知，小商场需处理退款业务。 @@ -378,45 +382,130 @@ EndNode.apply() → 组装结果并返回 TrialBalanceEntity 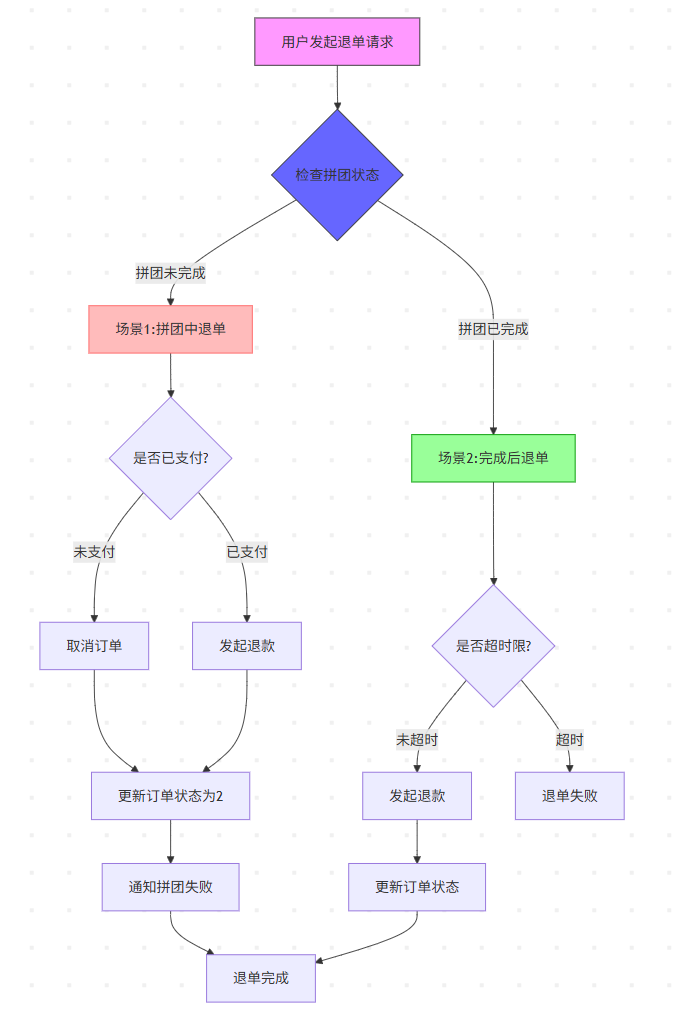image-20250725105608390 -逆向的流程，要分析用户是在哪个流程节点下进行中断行为。包括3个场景； +逆向的流程，要分析用户是在哪个流程节点下进行退单行为。包括3个场景； -**已锁单、未支付** +**已锁单、未支付**：redis恢复量+1，mysql中锁单量-1 -- **用户行为**：完成锁单后未发起支付。 -- **结果**：订单超时自动关单。 -- 补偿 - - 若用户在临界时刻支付，则需执行“逆向退款”流程——退还支付金额并告知“优惠已过期，请重新参与”。 - - 否则该订单自动失效，释放拼团名额给后续用户。 +**已锁单、已支付，但拼团未成团**：redis恢复量+1，mysql中锁单量、完成量-1，退款 -**已锁单、已支付，但拼团未成团** - -- **用户行为**：完成支付，组团人数不足暂未成团。 - -- 补偿策略 - - （可配置优先级）： - - 1. **先退拼团，再退款，** - 2. **先退款，再退拼团** - -- 具体执行哪种方式，可由拼团活动策略决定——“优先保障个人”或“优先保障成团”。 - -**已锁单、已支付，且拼团已成团** - -- **用户行为**：支付成功，且组团人数已凑齐。 -- 补偿流程 - - 先退还用户支付金额； - - 再撤销对应的拼团完成量。 -- **注意**：已成团订单视为“已完成含退单”，仍然成团、不再开放新用户参与，确保团队成团状态一致。 +**已锁单、已支付，且拼团已成团**：redis恢复量无需+1，因为成团之后不开放给别人；mysql中锁单量、完成量-1，退款，拼团设置为'已完成含退单'状态，但拼团中所有人都退单，更新为失败！ -### 策略模板应用 +### 核心流程说明 -根据订单状态和拼团状态动态选择退单策略。 +#### 阶段一：退单操作流程 +1. 客户**主动提交**退单请求 + +2. 通过责任链模式处理：数据加载Node（查询订单） → 重复检查Node（防止重复退单） → 策略执行Node + +3. 策略选择 + + 根据订单状态和拼团状态选择对应退单策略（三种之一） + +4. 执行退单 + + 更新**数据库**操作（锁单量、完成量、拼团状态、订单状态...） + +5. 消息通知 + 任务补偿 + + 发送MQ退单消息通知（未支付退单、已支付未成团...三种消息 notify_category） + + 将消息写入notify_task表，定时任务扫描未成功处理的消息，以做补偿兜底。 + +#### 阶段二：库存恢复流程 +6. 消息监听 + + MQ**监听器接收**退单成功消息 + +7. 服务调用 + + 调用恢复库存服务 + +8. 策略选择 + + 根据退单类型选择对应策略（已成团的无需恢复了，反正新用户也无法再参与该拼团） + +9. 库存恢复 + + 执行Redis库存恢复操作（带分布式锁保护） + +--- + +### 设计模式应用 + +1. **责任链模式** + + `TradeRefundRuleFilterFactory` 构建的过滤链： + `DataNodeFilter` → `UniqueRefundNodeFilter` → `RefundOrderNodeFilter` + +2. **策略模式** + + - 策略接口：`RefundOrderStrategy` + + - 实现策略： + + `Unpaid2RefundStrategy`（未付款退单的流程） + `Paid2RefundStrategy`（已付款退单） + `PaidTeam2RefundStrategy`（已成团退单） + +3. **工厂模式** + + `TradeRefundRuleFilterFactory` 负责组装责任链 + +4. **模板方法模式** + + `AbstractRefundOrderStrategy` 提供： + + - 公共方法封装 （发送退单MQ消息、库存恢复redis） + - 依赖注入支持 +### 退单触发入口 + +1）用户主动退单 + +2）定时任务，定时任务扫描锁单但未结算的订单，若支付时间超过设定值，对这笔订单执行退单操作。 + + + +```mermaid +flowchart LR + subgraph mall["小型支付商城"] + style mall fill:#ffffff,stroke:#333,stroke-width:2 + A[AliPayController
发起退单申请]:::blue + C[订单状态扭转
退单中]:::grey + E[RefundSuccessTopicListener
接收MQ消息
执行退款和订单状态变更]:::green + end + + subgraph pdd["拼团系统"] + style pdd fill:#ffffff,stroke:#333,stroke-width:2 + B[MarketTradeController
接收退单申请]:::yellow + D[TradeRefundOrderService
退单策略处理]:::red + F[TradeRepository
发送MQ消息]:::purple + G([MQ消息队列
退单成功消息]):::orange + H[RefundSuccessTopicListener
接收MQ消息
恢复库存]:::green + end + + A -- "1. 发起退单请求" --> B + B -- "2. 处理退单" --> D + D -- "3. 发送MQ消息" --> F + F -- "4. 发布消息 (异步+本地消息表补偿)" --> G + F -- "5. 返回结果" --> C + G -- "6. 消费消息 (恢复库存)" --> H + G -. "7. 消费消息 (执行退款)" .-> E + + classDef blue fill:#dbe9ff,stroke:#6fa1ff,stroke-width:1; + classDef grey fill:#e5e5e5,stroke:#9e9e9e,stroke-width:1; + classDef green fill:#d6f2d6,stroke:#76b076,stroke-width:1; + classDef yellow fill:#fef3cd,stroke:#f5c700,stroke-width:1; + classDef red fill:#f8d7da,stroke:#e55353,stroke-width:1; + classDef purple fill:#e4dbf9,stroke:#9370db,stroke-width:1; + classDef orange fill:#ffecca,stroke:#ffa500,stroke-width:1; + +``` + ## 收获 @@ -459,6 +548,60 @@ public class PayActivityEntity { +### 单例模式 + +**懒汉** + +```java +public class LazySingleton { + private static volatile LazySingleton instance; + + private LazySingleton() {} + + public static LazySingleton getInstance() { + if (instance == null) { // 第一次检查 + synchronized (LazySingleton.class) { + if (instance == null) { // 第二次检查 + instance = new LazySingleton(); + } + } + } + return instance; + } +} + +``` + +**饿汉** + +```java +public class EagerSingleton { + // 类加载时就初始化实例 + private static final EagerSingleton INSTANCE = new EagerSingleton(); + + // 私有构造函数 + private EagerSingleton() { + // 防止反射创建实例 + if (INSTANCE != null) { + throw new IllegalStateException("Singleton already initialized"); + } + } + + // 全局访问点 + public static EagerSingleton getInstance() { + return INSTANCE; + } + + // 防止反序列化破坏单例 + private Object readResolve() { + return INSTANCE; + } +} + +``` + + + ### 模板方法 **核心思想**： @@ -770,7 +913,7 @@ while 循环： ### 规则树流程 -!![image-20250725120957709](https://pic.bitday.top/i/2025/07/25/k01knr-0.png) +![image-20250725120957709](https://pic.bitday.top/i/2025/07/25/k01knr-0.png) **整体分层思路** @@ -1562,6 +1705,8 @@ public boolean tryOccupy(String counterKey, } ``` +本项目有两层防护：第一层是下单前的人数/库存校验，比较基础，由于前端可能更新不及时，显示还差X人拼团，但用户点进去时已达人数的情况。第二层是真正的并发保证，即**Redis 原子操作** + **后置校验／补偿**。 + ### `Supplier` @@ -1828,3 +1973,38 @@ output { +### RPC微服务调用 + +1.父Pom统一版本 + +```xml + + + org.apache.dubbo + dubbo-bom + 3.3.5 + pom + import + +``` + +2.pay-mall-infrustruct（Consumer）group-buying-sys-trigger (Provider)引入依赖 + +```xml + + + + org.apache.dubbo + dubbo-spring-boot-starter + + + + + org.apache.dubbo + dubbo-registry-nacos + + + +``` + +**** diff --git a/项目/智能协同云图库.md b/项目/智能协同云图库.md index 61b26d2..9801987 100644 --- a/项目/智能协同云图库.md +++ b/项目/智能协同云图库.md @@ -129,6 +129,103 @@ AI扩图 4、一些小问题的优化：比如 WebSocket 连接建立之后，如果用户退出了登录，这时 WebSocket 的连接是没有断开的。不过影响并不大，可以思考下怎么处理。 +## 踩坑 + +#### **精度损失和日期格式转换问题** + +##### **前端 → 后端** + +**日期** + +前端把日期格式化成后端期待的纯日期**字符串**，例如 `"2025-08-14"`，后端 DTO 用 `LocalDate` 接收（配合 `@JsonFormat(pattern="yyyy-MM-dd")`），Jackson 反序列化成 `LocalDate`。 + +**精度：** + +JavaScript 的 `number` 类型只能安全地表示到 2^53−1（约 9×10^15）的整数，超过这个范围就会丢失精度，用 `number` 传给后端时末尾只能补0； + +解决办法：前端 ID 当做字符串传给后端。 + +Spring MVC 会自动调用 `Long.parseLong("1951619197178556418")` 并赋值给你方法签名里的 `long id`（即还是写作long来接收，不变） + + + +##### **后端 → 前端** + +**日期：** + +后端用 `LocalDate` / `LocalDateTime` 之类的 Java 8 类型，经过 Jackson 序列化为指定格式的字符串（比如 `"yyyy-MM-dd"` / `"yyyy-MM-dd HH:mm:ss"`）供前端消费，避免时间戳或默认格式的不一致。 + +**精度：** + +Java 的 `long` 可能超过 JavaScript `number` 的安全范围（2^53−1），直接以数字输出会丢失精度。必须把 `long`/`Long` 序列化成**字符串**（例如 ID 输出为 `"1951648800160399362"`），前端拿到字符串再展示。 + + + +对 Jackson 用作 Spring 的 HTTP 消息转换器的 `ObjectMapper` 进行配置（日期格式、Java 8 时间支持、Long 转字符串等）示例代码： + +```java +@Configuration +public class JacksonConfig { + + private static final String DATE_FORMAT = "yyyy-MM-dd"; + private static final String DATETIME_FORMAT = "yyyy-MM-dd HH:mm:ss"; + private static final String TIME_FORMAT = "HH:mm:ss"; + + @Bean + public Jackson2ObjectMapperBuilderCustomizer jacksonCustomizer() { + return builder -> { + builder.featuresToDisable(DeserializationFeature.FAIL_ON_UNKNOWN_PROPERTIES); + builder.simpleDateFormat(DATETIME_FORMAT); + builder.featuresToDisable(SerializationFeature.WRITE_DATES_AS_TIMESTAMPS); + + JavaTimeModule javaTime = new JavaTimeModule(); + javaTime.addSerializer(LocalDateTime.class, + new LocalDateTimeSerializer(DateTimeFormatter.ofPattern(DATETIME_FORMAT))); + javaTime.addSerializer(LocalDate.class, + new LocalDateSerializer(DateTimeFormatter.ofPattern(DATE_FORMAT))); + javaTime.addSerializer(LocalTime.class, + new LocalTimeSerializer(DateTimeFormatter.ofPattern(TIME_FORMAT))); + javaTime.addDeserializer(LocalDateTime.class, + new LocalDateTimeDeserializer(DateTimeFormatter.ofPattern(DATETIME_FORMAT))); + javaTime.addDeserializer(LocalDate.class, + new LocalDateDeserializer(DateTimeFormatter.ofPattern(DATE_FORMAT))); + javaTime.addDeserializer(LocalTime.class, + new LocalTimeDeserializer(DateTimeFormatter.ofPattern(TIME_FORMAT))); + + SimpleModule longToString = new SimpleModule(); + longToString.addSerializer(Long.class, ToStringSerializer.instance); + longToString.addSerializer(Long.TYPE, ToStringSerializer.instance); + + builder.modules(javaTime, longToString); + }; + } + +} +``` + + + + + +**数据库密码加密** + +加密存储确保即使数据库泄露，攻击者也不能轻易获取用户原始密码。 + +spring security中提供了一个加密类**BCryptPasswordEncoder**。 + +它采用[哈希算法](https://so.csdn.net/so/search?q=哈希算法&spm=1001.2101.3001.7020) SHA-256 +随机盐+密钥对密码进行加密。加密算法是一种**可逆**的算法，而哈希算法是一种**不可逆**的算法。 + +因为有随机盐的存在，所以**相同的明文密码**经过加密后的密码是**不一样**的，盐在加密的密码中是有记录的，所以需要对比的时候，springSecurity是可以从中获取到盐的 + +验证密码 **matches** + +```java +// 使用 matches 方法来对比明文密码和存储的哈希密码 +boolean judge= passwordEncoder.matches(rawPassword, user.getPassword()); +``` + +注意，`matches`的第一个参数**必须** 是 “**原始明文**”，第二个参数 **必须** 是 “**已经加密过的密文**”！！！**顺序不能反！！！** + ## 收获 @@ -453,7 +550,9 @@ public String info() { } ``` -#### 多账号体系 + + +#### passwordEncoder多账号体系 若项目中存在两套权限校验体系。一套是 user 表的，分为普通用户和管理员；另一套是对团队空间的权限进行校验。 diff --git a/项目/苍穹外卖.md b/项目/苍穹外卖.md index 6eebf2f..dbad02c 100644 --- a/项目/苍穹外卖.md +++ b/项目/苍穹外卖.md @@ -834,15 +834,15 @@ net start winnat 直接部署开发完毕的前端代码，准备： -0.创建docker网络：`docker network create sky-net` +0）创建docker网络：`docker network create sky-net` -1.静态资源html文件夹(npm run build 打包源码获得) +1）静态资源html文件夹(npm run build 打包源码获得) -2.nginx.conf +2）nginx.conf ![image-20250515111352735](https://pic.bitday.top/i/2025/05/15/iexngr-0.png) -注意把nginx.conf中的server改为Docker 容器（或服务）在**同一网络中**的主机名，如 +注意把nginx.conf中的server改为Docker 容器（或服务）在**同一网络中**的服务名，如 ```nginx upstream webservers { @@ -852,7 +852,7 @@ upstream webservers { 因为同一个网络下的服务名会自动注册DNS，进行地址解析！ -3.docker-compose文件 +3）docker-compose文件 ```yml version: "3.8"