Commit on 2025/05/20 周二 19:32:40.56
This commit is contained in:
parent
e594fd9248
commit
bf6ae2a4e7
264
科研/ZY网络重构分析.md
264
科研/ZY网络重构分析.md
@ -14,6 +14,8 @@
|
||||
|
||||
2. 但仍然有 $n$ 个线性无关的特征向量(即可对角化)。
|
||||
|
||||
3. 特征值有正有负!!!
|
||||
|
||||
|
||||
|
||||
一个实对称矩阵可以通过其特征值和特征向量进行分解。对于一个 $n \times n$ 的**对称矩阵** $A$,
|
||||
@ -26,29 +28,32 @@ $$
|
||||
|
||||
$Q$是$n \times n$的正交矩阵,每一列是一个特征向量;$\Lambda$是$n \times n$的对角矩阵,对角线元素是特征值$\lambda_i$ ,其余为0。
|
||||
|
||||
其中,$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值,$x_i$ 是对应的特征向量。
|
||||
其中,$\lambda_i$ 是矩阵 $A$ 的第 $i$ 个特征值,$x_i$ 是对应的特征向量。**(注意!这里的特征向量需要归一化!!!)**
|
||||
|
||||
|
||||
|
||||
**事实上,如果矩阵 $A$ 的秩为 $r$ ,就只需要用前 $r$ 个特征值和特征向量就可以精确重构出。因为零特征值对矩阵重构不提供任何贡献。**
|
||||
**如果矩阵 $A$ 的秩为 $r$ ,那么谱分解里恰好有 $r$ 个非零特征值。**
|
||||
|
||||
用这 $r$ 对特征值/特征向量就能**精确**重构出 $A$,因为零特征值对矩阵重构不提供任何贡献。
|
||||
|
||||
因此,需要先对所有特征值取绝对值,从大到小排序,取前 $r$ 个!!!
|
||||
|
||||
|
||||
|
||||
**截断的谱分解**(取前 r 个特征值和特征向量)
|
||||
**截断的谱分解**(取前 $\kappa$ 个特征值和特征向量)
|
||||
|
||||
如果我们只保留前 $r$ 个最大的(或最重要的)特征值和对应的特征向量,那么:
|
||||
如果我们只保留前 $\kappa$ 个绝对值最大的特征值和对应的特征向量,那么:
|
||||
|
||||
- **特征向量矩阵 $U_r$**:取 $U$ 的前 $r$ 列,维度为 $n \times r$。
|
||||
- **特征值矩阵 $\Lambda_r$**:取 $\Lambda$ 的前 $r \times r$ 子矩阵(即前 $r$ 个对角线元素),维度为 $r \times r$。
|
||||
- **特征向量矩阵 $U_\kappa$**:取 $U$ 的前 $\kappa$ 列,维度为 $n \times \kappa$。
|
||||
- **特征值矩阵 $\Lambda_\kappa$**:取 $\Lambda$ 的前 $\kappa \times \kappa$ 子矩阵(即前 $\kappa$ 个对角线元素),维度为 $\kappa \times \kappa$。
|
||||
|
||||
因此,截断后的近似分解为:
|
||||
|
||||
$$
|
||||
A \approx U_r \Lambda_r U_r^T\\
|
||||
A \approx \sum_{i=1}^{r} \lambda_i x_i x_i^T
|
||||
A \approx U_\kappa \Lambda_\kappa U_\kappa^T\\
|
||||
A \approx \sum_{i=1}^{\kappa} \lambda_i x_i x_i^T
|
||||
$$
|
||||
|
||||
|
||||
**推导过程**
|
||||
|
||||
1. **特征值和特征向量的定义**
|
||||
@ -83,7 +88,7 @@ $$
|
||||
|
||||
可以写为
|
||||
$$
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
|
||||
A = \sum_{i=1}^{n} \lambda_i x_i x_i^T.
|
||||
$$
|
||||
|
||||
|
||||
@ -231,31 +236,40 @@ $$
|
||||
|
||||
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
|
||||
|
||||
真实矩阵 $A$ 与预测矩阵 $\widetilde{A} $ 之间的差为
|
||||
真实矩阵 $A$ 与预测矩阵 $\widetilde{A} $ 之间的差为 (秩为 $r$)
|
||||
$$
|
||||
A - \widetilde{A}=\sum_{m=1}^n \lambda_m\,x_m x_m^T-\sum_{m=1}^n \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T
|
||||
A - \widetilde{A}=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T
|
||||
$$
|
||||
若假设特征向量扰动可忽略,即$\widetilde x_m\approx x_m$ ,扰动可简化为(这里可能有问题,特征向量的扰动也要计算)
|
||||
**若假设特征向量扰动可忽略,即$\widetilde x_m\approx x_m$ ,扰动可简化为(这里可能有问题,特征向量的扰动也要计算)**
|
||||
$$
|
||||
A - \widetilde{A} = \sum_{m=1}^n \Delta \lambda_m \widetilde{x}_m \widetilde{x}_m^T.
|
||||
A - \widetilde{A} = \sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
对于任意元素 $(i, j)$ 上有
|
||||
$$
|
||||
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^n \Delta \lambda_m (\widetilde{x}_m \widetilde{x}_m^T)_{ij} \right| < \frac{1}{2}
|
||||
|a_{ij} - \widetilde{a}_{ij}|=\left| \sum_{m=1}^r \Delta \lambda_m ({x}_m {x}_m^T)_{ij} \right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
于一个归一化的特征向量 $\widetilde{x}_m$,其外积矩阵 $\widetilde{x}_m \widetilde{x}_m^T$ 的元素理论上满足
|
||||
于一个归一化的特征向量 ${x}_m$,其外积矩阵$ {x}_m {x}_m^T$ 满足
|
||||
$$
|
||||
|(\widetilde{x}_m \widetilde{x}_m^T)_{ij}| \leq 1.
|
||||
|({x}_m {x}_m^T)_{ij}| \leq 1.
|
||||
$$
|
||||
经过分析推导可以得出发生特征扰动时,网络精准重构条件为:
|
||||
例:
|
||||
$$
|
||||
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
|
||||
x_m = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\\
|
||||
x_m x_m^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
||||
$$
|
||||
每个元素的绝对值$\leq1$
|
||||
|
||||
|
||||
$$
|
||||
\Delta {\lambda} < \frac{1}{2n}
|
||||
\left| \sum_{m=1}^r \Delta \lambda_m (x_m x_m^T)_{ij} \right| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m|.
|
||||
$$
|
||||
为了确保 $|a_{ij} - \widetilde{a}_{ij}| < \frac{1}{2}$ 对所有 $(i,j)$ 成立,网络精准重构条件为:
|
||||
$$
|
||||
\sum_{m=1}^r\left| \Delta \lambda_m\right| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
||||
|
||||
@ -267,15 +281,16 @@ $$
|
||||
|
||||
### **非0/1矩阵**
|
||||
|
||||
#### **全局误差度量**
|
||||
#### **量化误差**
|
||||
|
||||
对估计矩阵 $\widetilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类,得到中心 $\{c_k\}_{k=1}^K$。
|
||||
对估计矩阵 $\tilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类,得到每个簇中心 $\{c_k\}_{k=1}^K$。
|
||||
|
||||
- **簇内平均偏差**:
|
||||
对于第 $k$簇,算该簇所有点到中心的平均绝对偏差:
|
||||
$$
|
||||
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
|
||||
$$
|
||||
|
||||
|
||||
- **全局允许误差**:
|
||||
$$
|
||||
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
|
||||
@ -283,42 +298,205 @@ $$
|
||||
|
||||
#### 带权重构需控制两类误差:
|
||||
|
||||
1. **截断谱分解误差**$\epsilon$:
|
||||
$$
|
||||
\epsilon
|
||||
= \bigl\|\widetilde A - A_r\bigr\|_F
|
||||
= \Bigl\|\sum_{m=r+1}^n \widetilde\lambda_m\,\widetilde x_m \widetilde x_m^T\Bigr\|_F.
|
||||
$$
|
||||
这里暂时忽略特征向量的扰动,即 $x_m=\widetilde x_m$
|
||||
|
||||
---
|
||||
|
||||
2. **滤波误差**$\eta$:
|
||||
1. **滤波误差**$\eta$:
|
||||
|
||||
**来源**:滤波器在谱域对真实特征值/向量的估计偏差,包括
|
||||
|
||||
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
|
||||
- 特征向量:矩阵扰动得来
|
||||
- **特征向量:矩阵扰动得来**
|
||||
- 设矩阵 $A$ 的秩为 $r$
|
||||
|
||||
$$
|
||||
A - \widetilde A=\sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
|
||||
A - \widetilde A=\sum_{m=1}^r \lambda_m\,x_m x_m^T-\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\sum_{m=1}^r \Delta \lambda_m {x}_m {x}_m^T.
|
||||
$$
|
||||
|
||||
$$
|
||||
\eta \approx \Bigl\|\sum_{m=1}^n \Delta\lambda_m\,\widetilde x_m\widetilde x_m^T\Bigr\|_F
|
||||
\Bigl\|\sum_{m=1}^r \Delta\lambda_m\, x_m x_m^T\Bigr\|_F = \sqrt{\sum_{m=1}^r (\Delta\lambda_m)^2}.
|
||||
$$
|
||||
|
||||
#### **最终约束条件**:
|
||||
|
||||
|
||||
2. **截断谱分解误差** $\epsilon$:
|
||||
只取前 $\kappa$ 个特征对重构
|
||||
|
||||
$$
|
||||
\boxed{
|
||||
\underbrace{\eta}_{\text{滤波误差}}
|
||||
\;+\;
|
||||
\underbrace{\epsilon}_{\text{谱分解截断误差}}
|
||||
\;\le\;
|
||||
\underbrace{\delta_{\max}}_{\text{聚类量化容限}}
|
||||
}
|
||||
A_\kappa \;=\;\sum_{m=1}^\kappa \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T=\;\sum_{m=1}^\kappa \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
$$
|
||||
\widetilde A - A_\kappa=\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T
|
||||
$$
|
||||
|
||||
|
||||
$$
|
||||
\Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.\epsilon
|
||||
= \Bigl\|\sum_{m=\kappa+1}^r \widetilde\lambda_m\, x_m x_m^T\Bigr\|_F=\sqrt{\sum_{m = \kappa + 1}^{r} \widetilde{\lambda}_{m}^{2}}.
|
||||
$$
|
||||
|
||||
|
||||
|
||||
3. **总的误差**
|
||||
$$
|
||||
\text{误差矩阵: } A - A_\kappa = \left( A - \widetilde{A} \right) + \left( \widetilde{A} - A_\kappa \right) = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
- 研究单个元素误差:
|
||||
$$
|
||||
\text{元素误差绝对值:}|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| \cdot |(x_m x_m^T)_{ij}| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m| \cdot |(x_m x_m^T)_{ij}|
|
||||
$$
|
||||
由于 $|(x_m x_m^T)_{ij}| \leq 1$(归一化特征向量):
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq \sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|
|
||||
$$
|
||||
|
||||
- 研究整个矩阵误差:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \left\| \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \right\|_F^2
|
||||
$$
|
||||
而 $\| x_m x_m^T \|_F = \sqrt{\text{tr}(x_m x_m^T x_m x_m^T)} = \sqrt{\text{tr}(x_m x_m^T)} = \| x_m \|_2 = 1$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2
|
||||
$$
|
||||
最终:
|
||||
$$
|
||||
\| A - A_\kappa \|_F = \sqrt{ \sum_{m=1}^r |\Delta \lambda_m|^2 + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|^2 }
|
||||
$$
|
||||
|
||||
|
||||
---
|
||||
|
||||
4. **最终约束条件**:
|
||||
|
||||
$$
|
||||
|(A - A_\kappa)_{ij}| \leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
$$
|
||||
\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### 量化阈值推导
|
||||
|
||||
要保证重构矩阵 $A_\kappa$ 在每个位置上“落到”正确的某一 簇而不搞混,就必须让重构误差的最大绝对值严格小于任意两个相邻量化级别之间的半距(half‐spacing)。具体地:
|
||||
|
||||
1. **量化级别及间距定义**
|
||||
设原始矩阵元素只能取 $K$ 个离散值:
|
||||
$$
|
||||
v_1 < v_2 < \cdots < v_K,
|
||||
$$
|
||||
相邻级别间距为:
|
||||
$$
|
||||
d_m = v_{m+1} - v_m,\quad m=1,\dots,K-1.
|
||||
$$
|
||||
|
||||
2. **最小间距确定**
|
||||
计算所有相邻级别的最小间距:
|
||||
$$
|
||||
d_{\min} = \min_{1\le m\le K-1} d_m.
|
||||
$$
|
||||
|
||||
3. **通用误差阈值**
|
||||
为确保重构值不会"越界"到相邻级别,取阈值:
|
||||
$$
|
||||
\boxed{\tau = \frac{d_{\min}}{2}.}
|
||||
$$
|
||||
|
||||
|
||||
**示例:**
|
||||
|
||||
1. 0-1矩阵,$a=0, b=1,K=2$,量化阈值为0.5。
|
||||
2. 量化级别 $\{0,\,0.3,\,0.7,\,1\}$ ,$K=4$ 时:
|
||||
- 相邻间距:$0.3, 0.4, 0.3$
|
||||
- $d_{\min}=0.3$,故 $\tau=0.15$
|
||||
|
||||
|
||||
|
||||
#### 维数选择推导
|
||||
|
||||
$$
|
||||
\sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde\lambda_m|\leq 量化阈值\tau
|
||||
$$
|
||||
|
||||
已知 $\sum_{m=1}^r |\Delta \lambda_m|=\eta$ ,量化阈值 $\tau$ ,令 $s=\tau-\eta$ ,设截断谱分解误差为 $\epsilon$
|
||||
$$
|
||||
\epsilon \leq \tau-\eta
|
||||
$$
|
||||
借助**前缀和+二分查找**寻找最小的 $\kappa$ :
|
||||
|
||||
1. **预处理:计算前缀和**
|
||||
设已经有绝对值降序的估计特征值列表
|
||||
$$
|
||||
a_m = \bigl|\widetilde\lambda_m\bigr|,\quad m=1,\dots,r,
|
||||
$$
|
||||
并算出它们的前缀和
|
||||
$$
|
||||
S_k = \sum_{m=1}^k a_m,\quad k=0,1,\dots,r,
|
||||
\quad S_0=0.
|
||||
$$
|
||||
同时总和 $S_r = \sum_{m=1}^r a_m$ 就是当 $\kappa=0$ 时的尾部累积(最大截断误差)。
|
||||
|
||||
2. **将「尾和 ≤ 预算 $s$」转成前缀和条件**
|
||||
记预算 $s = \tau - \eta$,尾部累积
|
||||
$$
|
||||
T(k) = \sum_{m=k+1}^r a_m = S_r - S_k.
|
||||
$$
|
||||
要 $T(k)\le s$,等价于
|
||||
$$
|
||||
S_k \;\ge\; S_r - s.
|
||||
$$
|
||||
令阈值
|
||||
$$
|
||||
\theta = S_r - s.
|
||||
$$
|
||||
|
||||
3. **二分查找最小 $\kappa$**
|
||||
在已排好序的数组 $S_k$(严格单调递增或非减)中,用二分查找找出最小的 $k$ 使得
|
||||
$$
|
||||
S_k \;\ge\;\theta.
|
||||
$$
|
||||
这个 $k$ 就是最小满足 $T(k)\le s$ 的截断秩 $\kappa$。
|
||||
|
||||
**伪代码:**
|
||||
|
||||
```python
|
||||
# 输入:绝对值降序的列表 a[1..r], 预算 s ≥ 0
|
||||
S = [0] * (r+1)
|
||||
for k in range(1, r+1):
|
||||
S[k] = S[k-1] + a[k] # 前缀和
|
||||
|
||||
theta = S[r] - s # 查找阈值
|
||||
# 在 S[0..r] 中二分找最小 k 使 S[k] >= theta
|
||||
low, high = 0, r
|
||||
while low < high:
|
||||
mid = (low + high) // 2
|
||||
if S[mid] < theta:
|
||||
low = mid + 1
|
||||
else:
|
||||
high = mid
|
||||
kappa = low
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
量化的间隔是不是就和分布有关,有无其他影响因素。
|
||||
|
||||
117
科研/线性代数.md
117
科研/线性代数.md
@ -676,18 +676,89 @@ $$
|
||||
\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} a_{ij}^2}
|
||||
$$
|
||||
|
||||
这个定义与向量 $L2$ 范数类似,只不过是对矩阵中所有元素取平方和后再开平方。
|
||||
这个定义与向量 $L2$ 范数类似,只不过是对矩阵中**所有元素取平方和后再开平方**。
|
||||
|
||||
|
||||
|
||||
对于**归一化**的向量$\mathbf{x}_m$ ,其外积矩阵 $\mathbf{x}_m \mathbf{x}_m^T$,其元素为 $(\mathbf{x}_m \mathbf{x}_m^T)_{ij} = x_i x_j$,因此:
|
||||
$$
|
||||
\|\mathbf{x}_m \mathbf{x}_m^T\|_F = \sqrt{\sum_{i=1}^n \sum_{j=1}^n |x_i x_j|^2 } = \sqrt{\left( \sum_{i=1}^n x_i^2 \right) \left( \sum_{j=1}^n x_j^2 \right) } = \|\mathbf{x}_m\|_2 \cdot \|\mathbf{x}_m\|_2 = 1.
|
||||
$$
|
||||
|
||||
例:
|
||||
|
||||
设归一化向量 $\mathbf{x} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}$,其外积矩阵为:
|
||||
$$
|
||||
\mathbf{x} \mathbf{x}^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}
|
||||
$$
|
||||
计算 Frobenius 范数:
|
||||
$$
|
||||
\|\mathbf{x} \mathbf{x}^T\|_F = \sqrt{ \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 } = \sqrt{4 \cdot \frac{1}{4}} = 1.
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
|
||||
|
||||
如果矩阵 $A$ 的奇异值为 $\sigma_1, \sigma_2, \ldots, \sigma_n$,则:
|
||||
|
||||
$$
|
||||
\|A\|_F = \sqrt{\sum_{i=1}^n \sigma_i^2}
|
||||
$$
|
||||
|
||||
这使得 Frobenius 范数在低秩近似和矩阵分解(如 SVD)中非常有用。
|
||||
|
||||
设矩阵 $A$ 为:
|
||||
$$
|
||||
A = \begin{bmatrix}
|
||||
1 & 0 \\
|
||||
0 & 2 \\
|
||||
1 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
定义:
|
||||
$$
|
||||
\|A\|_F = \sqrt{1^2 + 0^2 + 0^2 + 2^2 + 1^2 + 1^2 } = \sqrt{1 + 0 + 0 + 4 + 1 + 1} = \sqrt{7}
|
||||
$$
|
||||
验证:
|
||||
|
||||
1. 计算 $A^T A$:
|
||||
$$
|
||||
A^T A = \begin{bmatrix}
|
||||
1 & 0 & 1 \\
|
||||
0 & 2 & 1
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
1 & 0 \\
|
||||
0 & 2 \\
|
||||
1 & 1
|
||||
\end{bmatrix} = \begin{bmatrix}
|
||||
2 & 1 \\
|
||||
1 & 5
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
2. 求 $A^T A$ 的特征值(即奇异值的平方):
|
||||
$$
|
||||
\det(A^T A - \lambda I) = \lambda^2 - 7\lambda + 9 = 0 \implies \lambda = \frac{7 \pm \sqrt{13}}{2}
|
||||
$$
|
||||
因此:
|
||||
$$
|
||||
\sigma_1 = \sqrt{\frac{7 + \sqrt{13}}{2}}, \quad \sigma_2 = \sqrt{\frac{7 - \sqrt{13}}{2}}
|
||||
$$
|
||||
|
||||
3. 验证 Frobenius范数:
|
||||
$$
|
||||
\sigma_1^2 + \sigma_2^2 = \frac{7 + \sqrt{13}}{2} + \frac{7 - \sqrt{13}}{2} = 7
|
||||
$$
|
||||
所以:
|
||||
$$
|
||||
\|A\|_F = \sqrt{7}
|
||||
$$
|
||||
|
||||
|
||||
公式正确!
|
||||
|
||||
|
||||
|
||||
**迹和 Frobenius 范数的关系**:
|
||||
@ -698,41 +769,33 @@ $$
|
||||
|
||||
|
||||
|
||||
**权重为向量的情况**
|
||||
### 最大范数
|
||||
|
||||
当模型的输出是标量时(如单变量线性回归或二分类逻辑回归):
|
||||
|
||||
- **输入特征**:$\mathbf{x}_i \in \mathbb{R}^d$(向量)
|
||||
|
||||
- **权重形状**:$\mathbf{w} \in \mathbb{R}^d$(向量)
|
||||
|
||||
- **预测公式**:
|
||||
矩阵的最大范数(也称为 **元素级无穷范数** 或 **一致范数**)定义为矩阵所有元素绝对值的最大值:
|
||||
|
||||
$$
|
||||
\hat{y}_i = \mathbf{w}^\top \mathbf{x}_i
|
||||
\|A\|_{\max} = \max_{i,j} |A_{ij}|
|
||||
$$
|
||||
|
||||
其中 $\hat{y}_i$ 是标量输出。
|
||||
它衡量的是矩阵中**绝对值最大的元素**,适用于逐元素(element-wise)分析。
|
||||
|
||||
---
|
||||
|
||||
**权重为矩阵的情况**
|
||||
|
||||
当模型的输出是向量时(如多变量回归、神经网络全连接层):
|
||||
|
||||
- **输入特征**:$\mathbf{x}_i \in \mathbb{R}^d$(向量)
|
||||
|
||||
- **输出维度**:$\hat{\mathbf{y}}_i \in \mathbb{R}^m$(向量)
|
||||
|
||||
- **权重形状**:$W \in \mathbb{R}^{m \times d}$(矩阵)
|
||||
|
||||
- **预测公式**:
|
||||
如果比较两个矩阵 $A$ 和 $B$,它们的**误差矩阵** $E = A - B$ 的最大范数为:
|
||||
|
||||
$$
|
||||
\hat{\mathbf{y}}_i = W \mathbf{x}_i + \mathbf{b}
|
||||
\|A - B\|_{\max} = \max_{i,j} |A_{ij} - B_{ij}|
|
||||
$$
|
||||
|
||||
其中 $\mathbf{b} \in \mathbb{R}^m$ 是偏置向量。
|
||||
**意义**:
|
||||
|
||||
- 如果 $\|A - B\|_{\max} \leq \epsilon$,说明 $A$ 和 $B$ 的**所有对应元素的误差都不超过 $\epsilon$**。
|
||||
|
||||
|
||||
|
||||
对于任意 $m \times n$ 的矩阵 $A$,以下不等式成立:
|
||||
|
||||
$$
|
||||
\|A\|_{\max} \leq \|A\|_F \leq \sqrt{mn} \cdot \|A\|_{\max}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
77
科研/草稿.md
77
科研/草稿.md
@ -1,11 +1,70 @@
|
||||
$$
|
||||
\begin{align*}
|
||||
\sum_{m=1}^r \lambda_m x_m x_m^T + \sum_{m=r+1}^n \lambda_m x_m x_m^T = \sum_{m=1}^r \lambda_m x_m x_m^T
|
||||
\end{align*}
|
||||
$$
|
||||
### **研究整个矩阵的误差(全局误差分析)**
|
||||
|
||||
为了分析整个矩阵的重构误差 $A - A_\kappa$,我们可以采用不同的矩阵范数来衡量误差的大小。常见的选择包括:
|
||||
|
||||
1. **Frobenius 范数(F-范数)**:衡量矩阵所有元素的平方和,适用于整体误差分析。
|
||||
2. **谱范数(2-范数)**:衡量矩阵的最大奇异值,适用于最坏情况下的误差分析。
|
||||
3. **核范数(Trace 范数)**:衡量矩阵的奇异值之和,适用于低秩矩阵分析。
|
||||
|
||||
---
|
||||
|
||||
### **1. Frobenius 范数(F-范数)分析**
|
||||
F-范数定义为:
|
||||
$$
|
||||
\begin{align*}
|
||||
\lambda_{r+1}=\cdots=\lambda_n=0
|
||||
\end{align*}
|
||||
$$
|
||||
\| A - A_\kappa \|_F = \sqrt{\sum_{i,j} |(A - A_\kappa)_{ij}|^2}
|
||||
$$
|
||||
由于我们已经知道:
|
||||
$$
|
||||
A - A_\kappa = \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T
|
||||
$$
|
||||
我们可以计算其 F-范数:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \left\| \sum_{m=1}^r \Delta \lambda_m x_m x_m^T + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m x_m x_m^T \right\|_F^2
|
||||
$$
|
||||
由于 $x_m$ 是正交归一化的(假设 $x_i^T x_j = \delta_{ij}$),交叉项消失:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 \| x_m x_m^T \|_F^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2 \| x_m x_m^T \|_F^2
|
||||
$$
|
||||
而 $\| x_m x_m^T \|_F = \sqrt{\text{tr}(x_m x_m^T x_m x_m^T)} = \sqrt{\text{tr}(x_m x_m^T)} = \| x_m \|_2 = 1$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_F^2 = \sum_{m=1}^r \Delta \lambda_m^2 + \sum_{m=\kappa+1}^r \widetilde{\lambda}_m^2
|
||||
$$
|
||||
最终:
|
||||
$$
|
||||
\| A - A_\kappa \|_F \leq \sqrt{ \sum_{m=1}^r |\Delta \lambda_m|^2 + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|^2 }
|
||||
$$
|
||||
**结论**:
|
||||
- F-范数误差由特征值偏差和截断特征值的平方和决定。
|
||||
- 如果 $\Delta \lambda_m$ 和 $\widetilde{\lambda}_m$ 较小,F-范数误差也会较小。
|
||||
|
||||
---
|
||||
|
||||
### **2. 谱范数(2-范数)分析**
|
||||
谱范数定义为:
|
||||
$$
|
||||
\| A - A_\kappa \|_2 = \sigma_{\max}(A - A_\kappa)
|
||||
$$
|
||||
其中 $\sigma_{\max}$ 是最大奇异值。由于 $A - A_\kappa$ 是对称矩阵,其谱范数等于最大绝对特征值:
|
||||
$$
|
||||
\| A - A_\kappa \|_2 = \max \left\{ |\Delta \lambda_1|, \dots, |\Delta \lambda_r|, |\widetilde{\lambda}_{\kappa+1}|, \dots, |\widetilde{\lambda}_r| \right\}
|
||||
$$
|
||||
**结论**:
|
||||
- 谱范数误差由最大的特征值偏差或截断特征值决定。
|
||||
- 如果所有 $\Delta \lambda_m$ 和 $\widetilde{\lambda}_m$ 都较小,谱范数误差也会较小。
|
||||
|
||||
---
|
||||
|
||||
### **3. 核范数(Trace 范数)分析**
|
||||
核范数定义为:
|
||||
$$
|
||||
\| A - A_\kappa \|_* = \sum_{i=1}^r \sigma_i (A - A_\kappa)
|
||||
$$
|
||||
由于 $A - A_\kappa$ 的奇异值就是 $|\Delta \lambda_1|, \dots, |\Delta \lambda_r|, |\widetilde{\lambda}_{\kappa+1}|, \dots, |\widetilde{\lambda}_r|$,因此:
|
||||
$$
|
||||
\| A - A_\kappa \|_* = \sum_{m=1}^r |\Delta \lambda_m| + \sum_{m=\kappa+1}^r |\widetilde{\lambda}_m|
|
||||
$$
|
||||
**结论**:
|
||||
- 核范数误差等于特征值偏差和截断特征值的绝对值和。
|
||||
- 这与逐元素误差的界一致,但核范数衡量的是全局误差。
|
||||
|
||||
---
|
||||
@ -28,6 +28,8 @@ Docker为了解决依赖的兼容问题的,采用了两个手段:
|
||||
|
||||
#### DockerHub
|
||||
|
||||
http://dockerhub.com/
|
||||
|
||||
开源应用程序非常多,打包这些应用往往是重复的劳动。为了避免这些重复劳动,人们就会将自己打包的应用镜像,例如Redis、MySQL镜像放到网络上,共享使用,就像GitHub的代码共享一样。
|
||||
|
||||
- DockerHub:DockerHub是一个官方的Docker镜像的托管平台。这样的平台称为Docker Registry。
|
||||
@ -138,6 +140,7 @@ docker exec -it test-container sh
|
||||
|
||||
```text
|
||||
docker logs --since 1h test-container #查看最近1h
|
||||
docker logs --since 5m test-container #查看最近5分钟
|
||||
```
|
||||
|
||||
4.docker stop 停止正在运行的 test-container:
|
||||
@ -466,6 +469,10 @@ sudo systemctl restart docker
|
||||
systemctl show --property=Environment docker //验证是否配置成功
|
||||
```
|
||||
|
||||
经验总结:貌似配置代理+启动VPN没卵用,如果拉取不到镜像,还是老老实实配置国内镜像吧,另外注意GPT给出的镜像:tag是否真的存在!!!有时候可能是虚假的,根本拉不到。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### docker配置镜像:
|
||||
@ -904,11 +911,17 @@ docker-compose up --build -d
|
||||
|
||||
|
||||
|
||||
***!!注意在使用docker-compose命令时,可以指定服务名,而无需完整的容器名***
|
||||
***!!注意在使用docker-compose命令时,需要指定服务名,不能使用容器名!!!***
|
||||
|
||||
|
||||
|
||||
**查看服务的日志输出**
|
||||
**查看所有服务状态**
|
||||
|
||||
```shell
|
||||
docker-compose ps
|
||||
```
|
||||
|
||||
**查看服务的日志输出**(flask_app为服务名)
|
||||
|
||||
```shell
|
||||
docker-compose logs flask_app --since 1h #只显示最近 1 小时
|
||||
|
||||
@ -1441,6 +1441,8 @@ Nginx 将特定路径(例如 /api/)的请求转发到后端服务器。对
|
||||
|
||||
### JWT令牌
|
||||
|
||||

|
||||
|
||||
| 特性 | Session | JWT(JSON Web Token) |
|
||||
| -------- | ------------------------------------ | ----------------------------------------------- |
|
||||
| 存储方式 | 服务端存储会话数据(如内存、Redis) | 客户端存储完整的令牌(通常在 Header 或 Cookie) |
|
||||
|
||||
1159
自学/Mybatis&-Plus.md
Normal file
1159
自学/Mybatis&-Plus.md
Normal file
File diff suppressed because it is too large
Load Diff
403
自学/Mybatis.md
403
自学/Mybatis.md
@ -1,403 +0,0 @@
|
||||
## Mybatis
|
||||
|
||||
### 快速创建
|
||||
|
||||
|
||||
|
||||
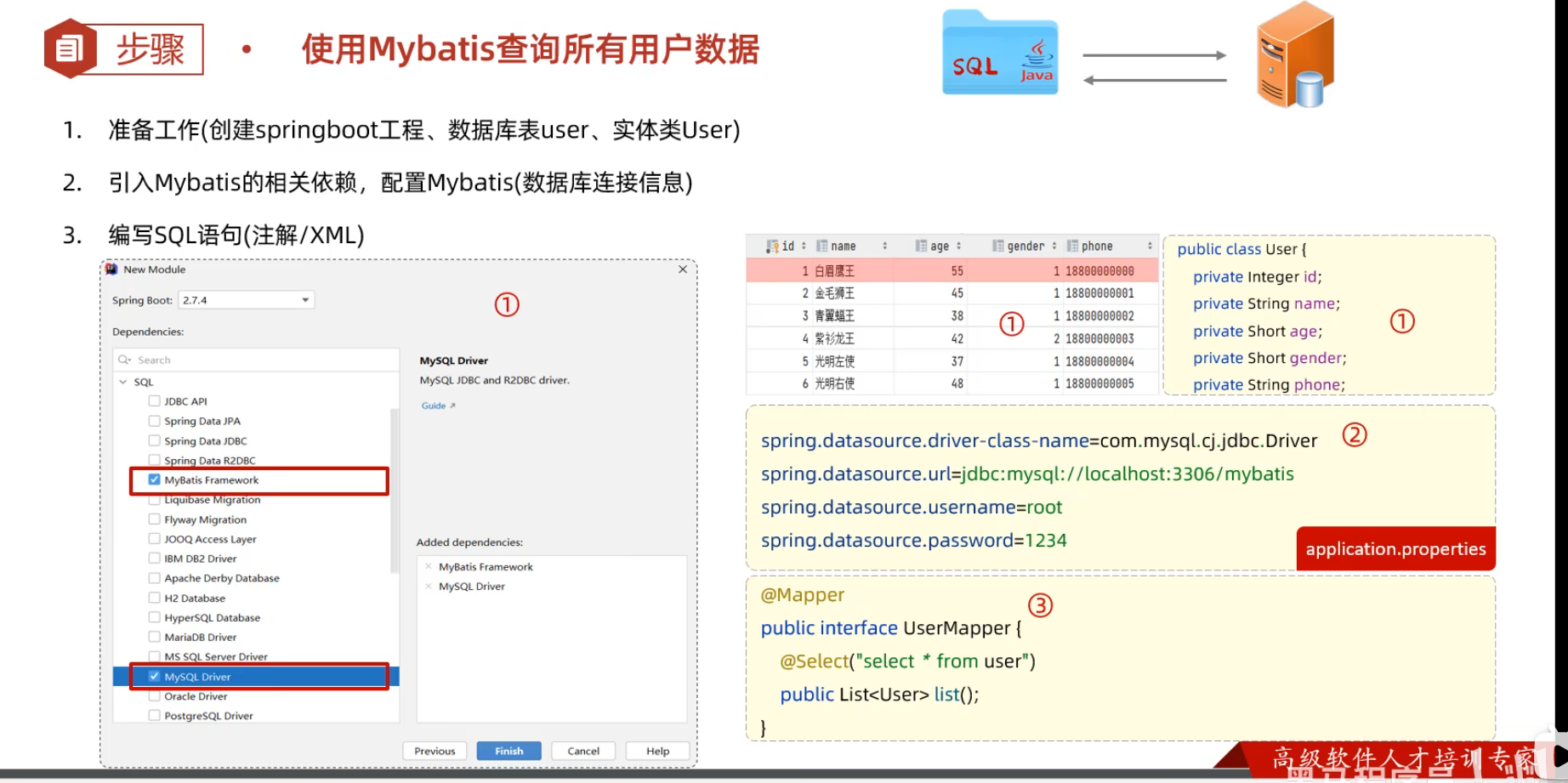
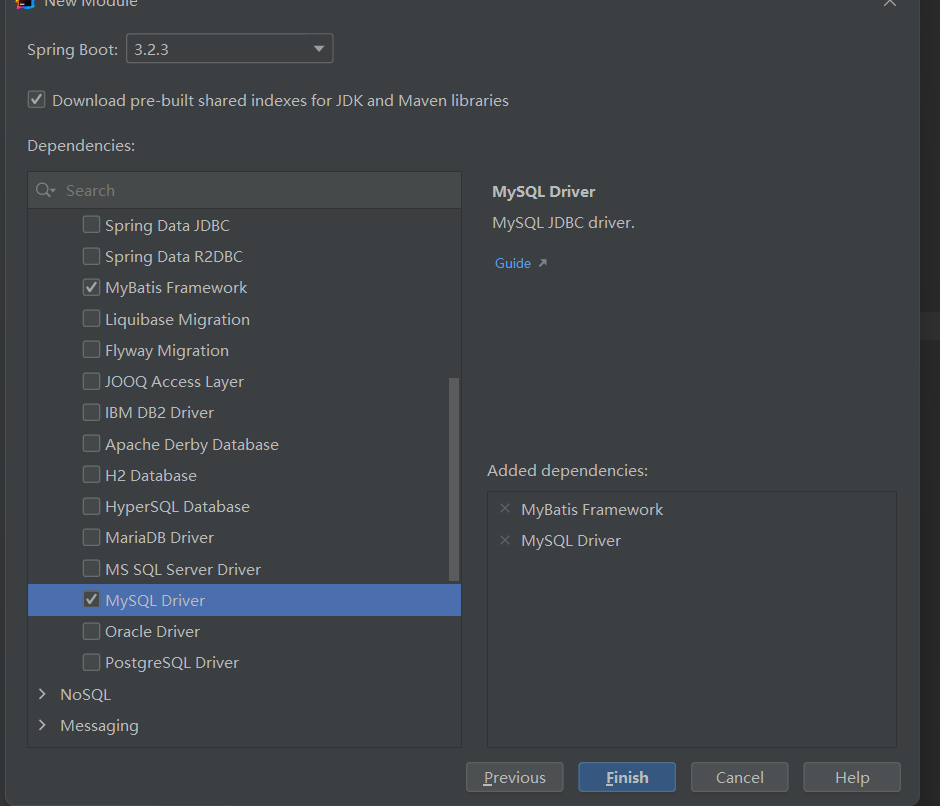
1. 创建springboot工程(Spring Initializr),并导入 mybatis的起步依赖、mysql的驱动包。创建用户表user,并创建对应的实体类User
|
||||
|
||||
|
||||
2. 在springboot项目中,可以编写main/resources/application.properties文件,配置数据库连接信息。
|
||||
|
||||
```
|
||||
#驱动类名称
|
||||
spring.datasource.driver-class-name=com.mysql.cj.jdbc.Driver
|
||||
#数据库连接的url
|
||||
spring.datasource.url=jdbc:mysql://localhost:3306/mybatis
|
||||
#连接数据库的用户名
|
||||
spring.datasource.username=root
|
||||
#连接数据库的密码
|
||||
spring.datasource.password=1234
|
||||
```
|
||||
|
||||
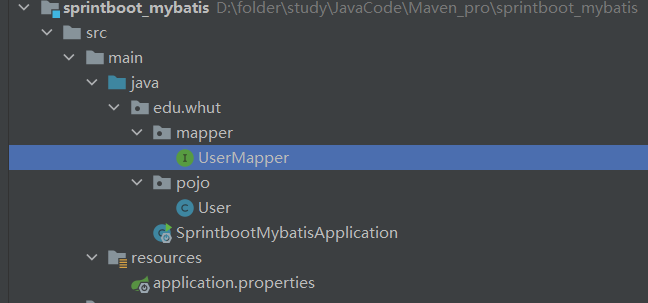
3. 在引导类所在包下,在创建一个包 mapper。在mapper包下创建一个接口 UserMapper
|
||||
|
||||
|
||||
|
||||
@Mapper注解:表示是mybatis中的Mapper接口
|
||||
|
||||
-程序运行时:框架会自动生成接口的**实现类对象(代理对象)**,并交给Spring的IOC容器管理
|
||||
|
||||
@Select注解:代表的就是select查询,用于书写select查询语句
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface UserMapper {
|
||||
//查询所有用户数据
|
||||
@Select("select * from user")
|
||||
public List<User> list();
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 数据库连接池
|
||||
|
||||
数据库连接池是一个容器,负责管理和分配数据库连接(`Connection`)。
|
||||
|
||||
- 在程序启动时,连接池会创建一定数量的数据库连接。
|
||||
- 客户端在执行 SQL 时,从连接池获取连接对象,执行完 SQL 后,将连接归还给连接池,以供其他客户端复用。
|
||||
- 如果连接对象长时间空闲且超过预设的最大空闲时间,连接池会自动释放该连接。
|
||||
|
||||
**优势**:避免频繁创建和销毁连接,提高数据库访问效率。
|
||||
|
||||
|
||||
|
||||
Druid(德鲁伊)
|
||||
|
||||
* Druid连接池是阿里巴巴开源的数据库连接池项目
|
||||
|
||||
* 功能强大,性能优秀,是Java语言最好的数据库连接池之一
|
||||
|
||||
把默认的 Hikari 数据库连接池切换为 Druid 数据库连接池:
|
||||
|
||||
1. 在pom.xml文件中引入依赖
|
||||
|
||||
```xml
|
||||
<dependency>
|
||||
<!-- Druid连接池依赖 -->
|
||||
<groupId>com.alibaba</groupId>
|
||||
<artifactId>druid-spring-boot-starter</artifactId>
|
||||
<version>1.2.8</version>
|
||||
</dependency>
|
||||
```
|
||||
|
||||
2. 在application.properties中引入数据库连接配置
|
||||
|
||||
```properties
|
||||
spring.datasource.druid.driver-class-name=com.mysql.cj.jdbc.Driver
|
||||
spring.datasource.druid.url=jdbc:mysql://localhost:3306/mybatis
|
||||
spring.datasource.druid.username=root
|
||||
spring.datasource.druid.password=123456
|
||||
```
|
||||
|
||||
|
||||
|
||||
### SQL注入问题
|
||||
|
||||
SQL注入:由于没有对用户输入进行充分检查,而SQL又是拼接而成,在用户输入参数时,在参数中添加一些SQL关键字,达到改变SQL运行结果的目的,也可以完成恶意攻击。
|
||||
|
||||
在Mybatis中提供的参数占位符有两种:${...} 、#{...}
|
||||
|
||||
- #{...}
|
||||
- 执行SQL时,会将#{…}替换为?,生成预编译SQL,会自动设置参数值
|
||||
- 使用时机:参数传递,都使用#{…}
|
||||
|
||||
- ${...}
|
||||
- 拼接SQL。直接将参数拼接在SQL语句中,**存在SQL注入问题**
|
||||
- 使用时机:如果对表名、列表进行动态设置时使用
|
||||
|
||||
|
||||
|
||||
### 日志输出
|
||||
|
||||
只建议开发环境使用:在Mybatis当中我们可以借助日志,查看到sql语句的执行、执行传递的参数以及执行结果
|
||||
|
||||
1. 打开application.properties文件
|
||||
|
||||
2. 开启mybatis的日志,并指定输出到控制台
|
||||
|
||||
```java
|
||||
#指定mybatis输出日志的位置, 输出控制台
|
||||
mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 驼峰命名法
|
||||
|
||||
在 Java 项目中,数据库表字段名一般使用 **下划线命名法**(snake_case),而 Java 中的变量名使用 **驼峰命名法**(camelCase)。
|
||||
|
||||
- [x] **小驼峰命名(lowerCamelCase)**:
|
||||
|
||||
- 第一个单词的首字母小写,后续单词的首字母大写。
|
||||
- **例子**:`firstName`, `userName`, `myVariable`
|
||||
|
||||
**大驼峰命名(UpperCamelCase)**:
|
||||
|
||||
- 每个单词的首字母都大写,通常用于类名或类型名。
|
||||
- **例子**:`MyClass`, `EmployeeData`, `OrderDetails`
|
||||
|
||||
|
||||
|
||||
表中查询的数据封装到实体类中
|
||||
|
||||
- 实体类属性名和数据库表查询返回的**字段名一致**,mybatis会自动封装。
|
||||
- 如果实体类属性名和数据库表查询返回的字段名不一致,不能自动封装。
|
||||
|
||||

|
||||
|
||||
解决方法:
|
||||
|
||||
1. 起别名
|
||||
2. 结果映射
|
||||
3. **开启驼峰命名**
|
||||
4. **属性名和表中字段名保持一致**
|
||||
|
||||
|
||||
|
||||
**开启驼峰命名(推荐)**:如果字段名与属性名符合驼峰命名规则,mybatis会自动通过驼峰命名规则映射
|
||||
|
||||
> 驼峰命名规则: abc_xyz => abcXyz
|
||||
>
|
||||
> - 表中字段名:abc_xyz
|
||||
> - 类中属性名:abcXyz
|
||||
|
||||
|
||||
|
||||
### 推荐的完整配置:
|
||||
|
||||
```yaml
|
||||
mybatis:
|
||||
#mapper配置文件
|
||||
mapper-locations: classpath:mapper/*.xml
|
||||
type-aliases-package: com.sky.entity
|
||||
configuration:
|
||||
#开启驼峰命名
|
||||
map-underscore-to-camel-case: true
|
||||
```
|
||||
|
||||
`type-aliases-package: com.sky.entity`把 `com.sky.entity` 包下的所有类都当作别名注册,XML 里就可以直接写 `<resultType="Dish">` 而不用写全限定名。可以多添加几个包,用逗号隔开。
|
||||
|
||||
|
||||
|
||||
### 增删改
|
||||
|
||||
- **增删改通用!:返回值为int时,表示影响的记录数,一般不需要可以设置为void!**
|
||||
|
||||
**作用于单个字段**
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface EmpMapper {
|
||||
//SQL语句中的id值不能写成固定数值,需要变为动态的数值
|
||||
//解决方案:在delete方法中添加一个参数(用户id),将方法中的参数,传给SQL语句
|
||||
/**
|
||||
* 根据id删除数据
|
||||
* @param id 用户id
|
||||
*/
|
||||
@Delete("delete from emp where id = #{id}")//使用#{key}方式获取方法中的参数值
|
||||
public void delete(Integer id);
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
上图参数值分离,有效防止SQL注入
|
||||
|
||||
|
||||
|
||||
**作用于多个字段**
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface EmpMapper {
|
||||
//会自动将生成的主键值,赋值给emp对象的id属性
|
||||
@Options(useGeneratedKeys = true,keyProperty = "id")
|
||||
@Insert("insert into emp(username, name, gender, image, job, entrydate, dept_id, create_time, update_time) values (#{username}, #{name}, #{gender}, #{image}, #{job}, #{entrydate}, #{deptId}, #{createTime}, #{updateTime})")
|
||||
public void insert(Emp emp);
|
||||
}
|
||||
```
|
||||
|
||||
在 **`@Insert`** 注解中使用 `#{}` 来引用 `Emp` 对象的属性,MyBatis 会自动从 `Emp` 对象中提取相应的字段并绑定到 SQL 语句中的占位符。
|
||||
|
||||
`@Options(useGeneratedKeys = true, keyProperty = "id")` 这行配置表示,插入时自动生成的主键会赋值给 `Emp` 对象的 `id` 属性。
|
||||
|
||||
```
|
||||
// 调用 mapper 执行插入操作
|
||||
empMapper.insert(emp);
|
||||
|
||||
// 现在 emp 对象的 id 属性会被自动设置为数据库生成的主键值
|
||||
System.out.println("Generated ID: " + emp.getId());
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 查
|
||||
|
||||
查询案例:
|
||||
|
||||
- **姓名:要求支持模糊匹配**
|
||||
- 性别:要求精确匹配
|
||||
- 入职时间:要求进行范围查询
|
||||
- 根据最后修改时间进行降序排序
|
||||
|
||||
重点在于模糊查询时where name like '%#{name}%' 会报错。
|
||||
|
||||
解决方案:
|
||||
|
||||
使用MySQL提供的字符串拼接函数:`concat('%' , '关键字' , '%')`
|
||||
|
||||
**`CONCAT()`** 如果其中任何一个参数为 **`NULL`**,`CONCAT()` 返回 **`NULL`**,`Like NULL`会导致查询不到任何结果!
|
||||
|
||||
`NULL`和`''`是完全不同的
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface EmpMapper {
|
||||
|
||||
@Select("select * from emp " +
|
||||
"where name like concat('%',#{name},'%') " +
|
||||
"and gender = #{gender} " +
|
||||
"and entrydate between #{begin} and #{end} " +
|
||||
"order by update_time desc")
|
||||
public List<Emp> list(String name, Short gender, LocalDate begin, LocalDate end);
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### XML配置文件规范
|
||||
|
||||
使用Mybatis的注解方式,主要是来完成一些简单的增删改查功能。如果需要实现复杂的SQL功能,建议使用XML来配置映射语句,也就是将SQL语句写在XML配置文件中。
|
||||
|
||||
在Mybatis中使用XML映射文件方式开发,需要符合一定的规范:
|
||||
|
||||
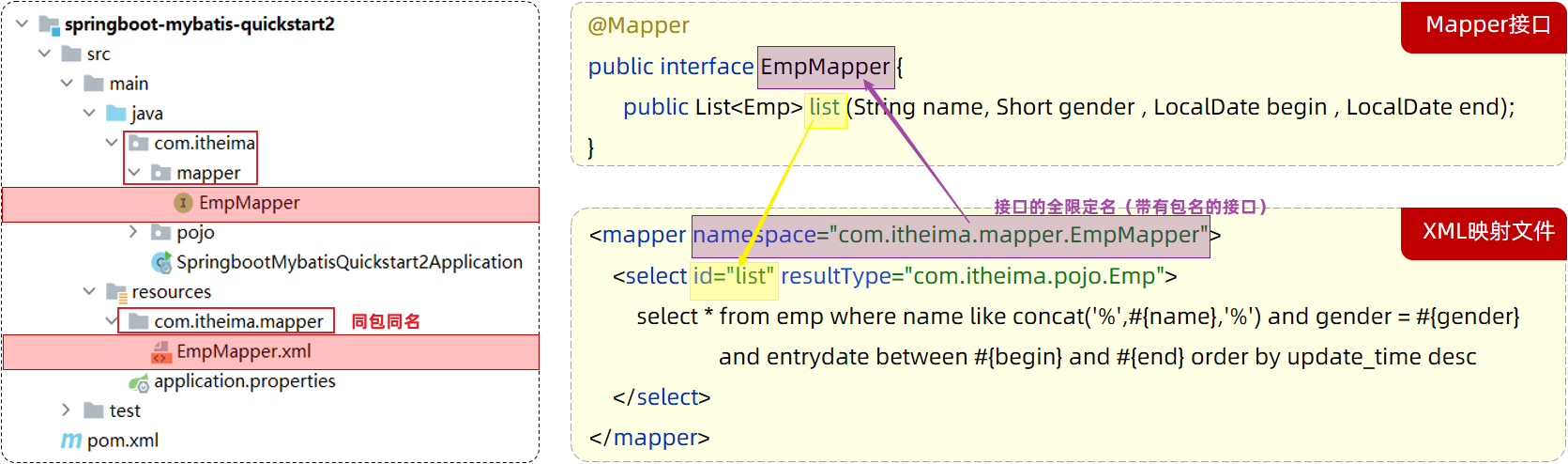
1. XML映射**文件的名称**与Mapper**接口名称**一致,并且将XML映射文件和Mapper接口放置在相同包下(同包同名)
|
||||
|
||||
2. XML映射文件的**namespace属性**为Mapper接口**全限定名**一致
|
||||
|
||||
3. XML映射文件中sql语句的**id**与Mapper接口中的**方法名**一致,并保持返回类型一致。
|
||||
|
||||
|
||||
|
||||
\<select>标签:就是用于编写select查询语句的。
|
||||
|
||||
resultType属性,指的是查询返回的单条记录所封装的类型(查询必须)。
|
||||
|
||||
parameterType属性(可选,MyBatis 会根据接口方法的入参类型(比如 `Dish` 或 `DishPageQueryDTO`)自动推断),POJO作为入参,需要使用全类名或是`type‑aliases‑package: com.sky.entity` 下注册的别名。
|
||||
|
||||
```
|
||||
<insert id="insert" useGeneratedKeys="true" keyProperty="id">
|
||||
<select id="pageQuery" resultType="com.sky.vo.DishVO">
|
||||
<select id="list" resultType="com.sky.entity.Dish" parameterType="com.sky.entity.Dish">
|
||||
```
|
||||
|
||||
|
||||
|
||||
**实现过程:**
|
||||
|
||||
1. resources下创与java下一样的包,即edu/whut/mapper,新建xx.xml文件
|
||||
|
||||
2. 配置Mapper文件
|
||||
|
||||
```xml
|
||||
<?xml version="1.0" encoding="UTF-8" ?>
|
||||
<!DOCTYPE mapper
|
||||
PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN"
|
||||
"https://mybatis.org/dtd/mybatis-3-mapper.dtd">
|
||||
<mapper namespace="edu.whut.mapper.EmpMapper">
|
||||
<!-- SQL 查询语句写在这里 -->
|
||||
</mapper>
|
||||
```
|
||||
|
||||
`namespace` 属性指定了 **Mapper 接口的全限定名**(即包名 + 类名)。
|
||||
|
||||
3. 编写查询语句
|
||||
|
||||
```xml
|
||||
<select id="list" resultType="edu.whut.pojo.Emp">
|
||||
select * from emp
|
||||
where name like concat('%',#{name},'%')
|
||||
and gender = #{gender}
|
||||
and entrydate between #{begin} and #{end}
|
||||
order by update_time desc
|
||||
</select>
|
||||
```
|
||||
|
||||
**`id="list"`**:指定查询方法的名称,应该与 Mapper 接口中的方法名称一致。
|
||||
|
||||
**`resultType="edu.whut.pojo.Emp"`**:`resultType` 只在 **查询操作** 中需要指定。指定查询结果映射的对象类型,这里是 `Emp` 类。
|
||||
|
||||
|
||||
|
||||
这里有bug!!!
|
||||
|
||||
`concat('%',#{name},'%')`这里应该用`<where>` `<if>`标签对name是否为`NULL`或`''`进行判断
|
||||
|
||||
|
||||
|
||||
### 动态SQL
|
||||
|
||||
#### SQL-if,where
|
||||
|
||||
`<if>`:用于判断条件是否成立。使用test属性进行条件判断,如果条件为true,则拼接SQL。
|
||||
|
||||
~~~xml
|
||||
<if test="条件表达式">
|
||||
要拼接的sql语句
|
||||
</if>
|
||||
~~~
|
||||
|
||||
`<where>`只会在子元素有内容的情况下才插入where子句,而且会自动去除子句的开头的AND或OR,**加了总比不加好**
|
||||
|
||||
```java
|
||||
<select id="list" resultType="com.itheima.pojo.Emp">
|
||||
select * from emp
|
||||
<where>
|
||||
<!-- if做为where标签的子元素 -->
|
||||
<if test="name != null">
|
||||
and name like concat('%',#{name},'%')
|
||||
</if>
|
||||
<if test="gender != null">
|
||||
and gender = #{gender}
|
||||
</if>
|
||||
<if test="begin != null and end != null">
|
||||
and entrydate between #{begin} and #{end}
|
||||
</if>
|
||||
</where>
|
||||
order by update_time desc
|
||||
</select>
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### SQL-foreach
|
||||
|
||||
Mapper 接口
|
||||
|
||||
```java
|
||||
@Mapper
|
||||
public interface EmpMapper {
|
||||
//批量删除
|
||||
public void deleteByIds(List<Integer> ids);
|
||||
}
|
||||
```
|
||||
|
||||
XML 映射文件
|
||||
|
||||
`<foreach>` 标签用于遍历集合,常用于动态生成 SQL 语句中的 IN 子句、批量插入、批量更新等操作。
|
||||
|
||||
```java
|
||||
<foreach collection="集合名称" item="集合遍历出来的元素/项" separator="每一次遍历使用的分隔符"
|
||||
open="遍历开始前拼接的片段" close="遍历结束后拼接的片段">
|
||||
</foreach>
|
||||
```
|
||||
|
||||
`open="("`:这个属性表示,在*生成的 SQL 语句开始*时添加一个 左括号 `(`。
|
||||
|
||||
`close=")"`:这个属性表示,在生成的 SQL 语句结束时添加一个 右括号 `)`。
|
||||
|
||||
例:批量删除实现
|
||||
|
||||
```java
|
||||
<delete id="deleteByIds">
|
||||
DELETE FROM emp WHERE id IN
|
||||
<foreach collection="ids" item="id" separator="," open="(" close=")">
|
||||
#{id}
|
||||
</foreach>
|
||||
</delete>
|
||||
```
|
||||
|
||||
实现效果类似:`DELETE FROM emp WHERE id IN (1, 2, 3);`
|
||||
@ -635,7 +635,7 @@ proxies:
|
||||
|
||||
|
||||
|
||||
**启动Clash**
|
||||
### **启动Clash**
|
||||
|
||||
```text
|
||||
./CrashCore -d . & //后台启动
|
||||
@ -694,7 +694,7 @@ sudo systemctl status clash
|
||||
|
||||
|
||||
|
||||
**配置YACD**
|
||||
### **配置YACD**
|
||||
|
||||
YACD 是一个基于 **Clash** 的 Web 管理面板,用于管理您的 Clash 配置、查看流量和节点信息等。
|
||||
|
||||
@ -730,7 +730,6 @@ nohup pnpm serve --host 0.0.0.0 & //如果不是0.0.0.0 不能在windows上
|
||||
|
||||
```text
|
||||
ps aux | grep pnpm
|
||||
|
||||
kill xxx
|
||||
```
|
||||
|
||||
@ -738,9 +737,17 @@ kill xxx
|
||||
|
||||
通过http://124.71.159.195:4173/ 访问yacd控制面板。手动添加crash服务所在的ip:端口。
|
||||
|
||||
如果连不上:yacd和crash都是http协议就行了。
|
||||
|
||||
|
||||
**如果连不上**:yacd面板和crash都是http协议就行了。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 连接测试
|
||||
|
||||
直连: curl -v https://www.google.com
|
||||
|
||||
使用代理:curl -x http://127.0.0.1:7890 https://www.google.com
|
||||
|
||||
|
||||
@ -430,6 +430,20 @@ counts.put(ch, counts.getOrDefault(ch, 0) + 1);
|
||||
|
||||
|
||||
|
||||
如何从List中初始化Set?
|
||||
|
||||
```java
|
||||
Set<String> set1 = new HashSet<>(wordList); //构造器直接初始化
|
||||
```
|
||||
|
||||
如何从Array中初始化?
|
||||
|
||||
```java
|
||||
Set<String> set1 = new HashSet<>(Arrays.asList(wordList)); //构造器直接初始化
|
||||
```
|
||||
|
||||
|
||||
|
||||
### PriorityQueue
|
||||
|
||||
- 基于优先堆(最小堆或最大堆)实现,元素按优先级排序。
|
||||
@ -935,9 +949,11 @@ public class QueueExample {
|
||||
|
||||
### Deque(双端队列+栈)
|
||||
|
||||
支持在队列的两端(头和尾)进行元素的插入和删除。这使得 Deque 既能作为队列(FIFO)又能作为栈(LIFO)使用。
|
||||
支持在队列的两端(头和尾)进行元素的插入和删除。这使得 **Deque 既能作为队列(FIFO)又能作为栈(LIFO)使用。**栈可以看作双端队列的特例,即使用一端。
|
||||
|
||||
建议在需要栈操作时使用 `Deque` 的实现
|
||||
- **LinkedList** 是基于双向链表实现的,每个节点存储数据和指向前后节点的引用。
|
||||
- **ArrayDeque** 则基于动态数组实现,内部使用循环数组来存储数据。
|
||||
- **ArrayDeque** 在大多数情况下性能更好,因为数组在内存中连续,缓存友好,且操作(如 push/pop)开销更小。
|
||||
|
||||
**栈**
|
||||
|
||||
@ -949,50 +965,42 @@ Integer top1=stack.peek()
|
||||
Integer top = stack.pop(); // 出栈
|
||||
```
|
||||
|
||||
- **LinkedList** 是基于双向链表实现的,每个节点存储数据和指向前后节点的引用。
|
||||
- **ArrayDeque** 则基于动态数组实现,内部使用循环数组来存储数据。
|
||||
- **ArrayDeque** 在大多数情况下性能更好,因为数组在内存中连续,缓存友好,且操作(如 push/pop)开销更小。
|
||||
|
||||
|
||||
|
||||
**双端队列**
|
||||
|
||||
*在队头操作*
|
||||
|
||||
- `addFirst(E e)`:在队头添加元素,如果操作失败会抛出异常。
|
||||
- `offerFirst(E e)`:在队头插入元素,返回 `true` 或 `false` 表示是否成功。
|
||||
- `offerFirst(E e)`:**在队头插入元素**,返回 `true` 或 `false` 表示是否成功。
|
||||
- `peekFirst()`:查看队头元素,不移除;队列为空返回 `null`。
|
||||
- `removeFirst()`:移除并返回队头元素;队列为空会抛出异常。
|
||||
- `pollFirst()`:移除并返回队头元素;队列为空返回 `null`。
|
||||
|
||||
*在队尾操作*
|
||||
|
||||
- `addLast(E e)`:在队尾添加元素,若失败会抛出异常。
|
||||
- `offerLast(E e)`:在队尾插入元素,返回 `true` 或 `false` 表示是否成功。
|
||||
- `peekLast()`:查看队尾元素,不移除;队列为空返回 `null`。
|
||||
- `removeLast()`:移除并返回队尾元素;队列为空会抛出异常。
|
||||
- `pollLast()`:移除并返回队尾元素;队列为空返回 `null`。
|
||||
|
||||
|
||||
|
||||
*添加元素*:调用 `add(e)` 或 `offer(e)` 时,实际上是调用 `addLast(e)` 或 `offerLast(e)`,即在**队尾**添加元素。
|
||||
*添加元素*:调用 `offer(e)` 时,实际上是调用 `offerLast(e)`,即在**队尾**添加元素。push(e)` ⇒ 等价于 `addFirst(e)
|
||||
|
||||
*删除或查看元素*:调用 `remove()` 或 `poll()` 时,则是调用 `removeFirst()` 或 `pollFirst()`,即在队头移除元素;同理,`element()` 或 `peek()` 则是查看队头元素。
|
||||
*删除或查看元素*:调用`poll()` 时,则是调用 `pollFirst()`,即在队头移除元素;同理, `peek()` 则是查看队头元素。
|
||||
|
||||
```java
|
||||
import java.util.Deque;
|
||||
import java.util.LinkedList;
|
||||
import java.util.ArrayDeque;
|
||||
|
||||
public class DequeExample {
|
||||
public static void main(String[] args) {
|
||||
// 使用 LinkedList 实现双端队列
|
||||
Deque<Integer> deque = new LinkedList<>();
|
||||
// 使用 ArrayDeque 实现双端队列
|
||||
Deque<Integer> deque = new ArrayDeque<>();
|
||||
|
||||
// 在队列头部添加元素
|
||||
deque.addFirst(10);
|
||||
// 在队列尾部添加元素
|
||||
deque.addLast(20);
|
||||
// 在队列头部插入元素
|
||||
// 在队列头部插入元素(和 addFirst 类似,但失败时不会抛异常)
|
||||
deque.offerFirst(5);
|
||||
// 在队列尾部插入元素
|
||||
deque.offerLast(30);
|
||||
|
||||
407
自学/微服务.md
407
自学/微服务.md
@ -1,406 +1,49 @@
|
||||
# 微服务
|
||||
|
||||
## Mybatis-Plus
|
||||
## 认识微服务
|
||||
|
||||
### 快速开始
|
||||
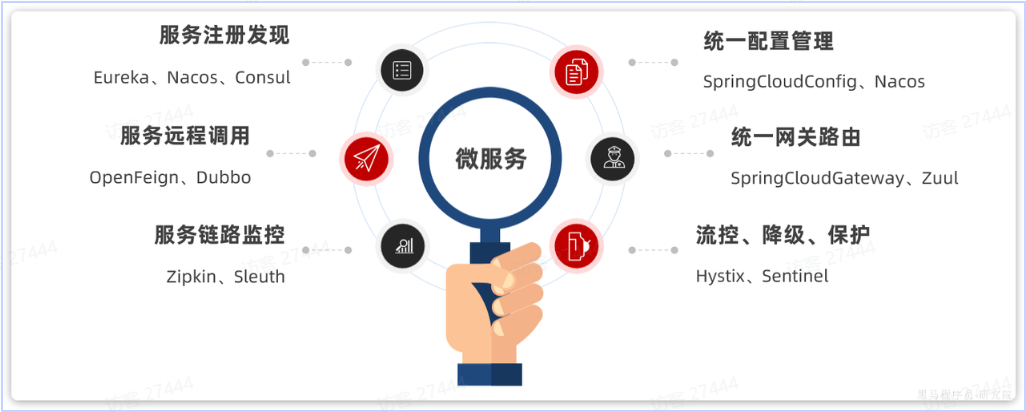
微服务架构,首先是服务化,就是将单体架构中的功能模块从单体应用中拆分出来,独立部署为多个服务。
|
||||
|
||||
**1.引入依赖**
|
||||
<img src="https://pic.bitday.top/i/2025/05/20/iyyuzk-0.png" alt="image-20250520114708790" style="zoom:67%;" />
|
||||
|
||||
```XML
|
||||
<dependency>
|
||||
<groupId>com.baomidou</groupId>
|
||||
<artifactId>mybatis-plus-boot-starter</artifactId>
|
||||
<version>3.5.3.1</version>
|
||||
</dependency>
|
||||
```
|
||||
**SpringCloud**
|
||||
|
||||
由于这个starter包含对mybatis的自动装配,因此完全可以替换掉Mybatis的starter。
|
||||
|
||||
|
||||
**2.定义mapper**
|
||||
使用Spring Cloud 2021.0.x以及Spring Boot 2.7.x版本(需要对应)。
|
||||
|
||||
修改mp-demo中的`com.itheima.mp.mapper`包下的`UserMapper`接口,让其继承`BaseMapper`:
|
||||
<img src="https://pic.bitday.top/i/2025/05/20/knttz4-0.png" alt="image-20250520124938379" style="zoom:80%;" />
|
||||
|
||||
```text
|
||||
public interface UserMapper extends BaseMapper<User> {
|
||||
}
|
||||
```
|
||||
<img src="https://pic.bitday.top/i/2025/05/20/knvz3s-0.png" alt="image-20250520124948604" style="zoom:80%;" />
|
||||
|
||||
在父pom中的`<dependencyManagement>`锁定版本,使得后续你在子模块里引用 Spring Cloud 或 Spring Cloud Alibaba 的各个组件时,不需要再写 `<version>`,Maven 会统一采用你在父 POM 中指定的版本。
|
||||
|
||||
|
||||
MybatisPlus如何知道我们要查询的是哪张表?表中有哪些字段呢?
|
||||
|
||||
**约定大于配置**
|
||||
## 微服务拆分
|
||||
|
||||
**泛型中的User**就是与数据库对应的PO.
|
||||
微服务拆分时:
|
||||
|
||||
MybatisPlus就是根据PO实体的信息来推断出表的信息,从而生成SQL的。默认情况下:
|
||||
- **高内聚**:每个微服务的职责要尽量单一,包含的业务相互关联度高、完整度高。
|
||||
- **低耦合**:每个微服务的功能要相对独立,尽量减少对其它微服务的依赖,或者依赖接口的稳定性要强。
|
||||
|
||||
- MybatisPlus会把PO实体的**类名**驼峰转下划线作为**表名**
|
||||
- MybatisPlus会把PO实体的所有**变量名**驼峰转下划线作为表的**字段名**,并根据变量类型推断字段类型
|
||||
- MybatisPlus会把名为**id**的字段作为**主键**
|
||||
<img src="https://pic.bitday.top/i/2025/05/20/m06nzx-0.png" alt="image-20250520133100419" style="zoom:67%;" />
|
||||
|
||||
但很多情况下,默认的实现与实际场景不符,因此MybatisPlus提供了一些注解便于我们声明表信息。
|
||||
**一般微服务项目有两种不同的工程结构:**
|
||||
|
||||
**3.常见注解**
|
||||
- [ ] 完全解耦:每一个微服务都创建为一个**独立的工程**,甚至可以使用不同的开发语言来开发,项目完全解耦。
|
||||
- 优点:服务之间耦合度低
|
||||
- 缺点:每个项目都有自己的独立仓库,管理起来比较麻烦
|
||||
- [x] **Maven聚合**:整个项目为一个Project,然后每个微服务是其中的**一个Module**
|
||||
- 优点:项目代码集中,管理和运维方便
|
||||
- 缺点:服务之间耦合,编译时间较长
|
||||
|
||||
**@TableName**
|
||||
|
||||
- 描述:表名注解,标识实体类对应的表
|
||||
- 使用位置:实体类
|
||||
|
||||
```Java
|
||||
@TableName("user")
|
||||
public class User {
|
||||
private Long id;
|
||||
private String name;
|
||||
}
|
||||
```
|
||||
IDEA配置小技巧:
|
||||
|
||||
**@TableId**
|
||||
1.自动导包
|
||||
|
||||
- 描述:主键注解,标识实体类中的主键字段
|
||||
- 使用位置:实体类的主键字段
|
||||
|
||||
`TableId`注解支持两个属性:
|
||||
|
||||
| **属性** | **类型** | **必须指定** | **默认值** | **描述** |
|
||||
| :------- | :------- | :----------- | :---------- | :----------- |
|
||||
| value | String | 否 | "" | 主键字段名 |
|
||||
| type | Enum | 否 | IdType.NONE | 指定主键类型 |
|
||||
|
||||
```text
|
||||
@TableName("user")
|
||||
public class User {
|
||||
@TableId(value="id",type=IdType.AUTO)
|
||||
private Long id;
|
||||
private String name;
|
||||
}
|
||||
```
|
||||
|
||||
必须指定type=IdType.AUTO,默认是雪花算法算出一个随机的id(插入操作时)
|
||||
|
||||
|
||||
|
||||
**@TableField**
|
||||
|
||||
一般情况下我们并不需要给字段添加`@TableField`注解,一些特殊情况除外:
|
||||
|
||||
- 成员变量名与数据库字段名不一致
|
||||
- 成员变量是以`isXXX`命名,按照`JavaBean`的规范,`MybatisPlus`识别字段时会把`is`去除,这就导致与数据库不符。
|
||||
- 成员变量名与数据库一致,但是与数据库的**关键字(如order)**冲突。使用`@TableField`注解给字段名添加转义字符:````
|
||||
|
||||
支持的其它属性如下:
|
||||
|
||||
exist:默认为true,表示是数据库字段,若
|
||||
|
||||
```text
|
||||
@TableField(exist=false)
|
||||
private String address;
|
||||
```
|
||||
|
||||
将自动跳过address的增删查改,因为它不被视为字段。
|
||||
|
||||
|
||||
|
||||
```Java
|
||||
@TableName("user")
|
||||
public class User {
|
||||
@TableId
|
||||
private Long id;
|
||||
private String name;
|
||||
private Integer age;
|
||||
@TableField("isMarried")
|
||||
private Boolean isMarried;
|
||||
@TableField("`order`")
|
||||
private String order;
|
||||
}
|
||||
```
|
||||
|
||||
### 常见配置
|
||||
|
||||
大多数的配置都有默认值,因此我们都无需配置。但还有一些是没有默认值的,例如:
|
||||
|
||||
- 实体类的别名扫描包
|
||||
- 全局id类型
|
||||
|
||||
要改也就改这两个即可
|
||||
|
||||
```YAML
|
||||
mybatis-plus:
|
||||
type-aliases-package: com.itheima.mp.domain.po
|
||||
global-config:
|
||||
db-config:
|
||||
id-type: auto # 全局id类型为自增长
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 核心功能
|
||||
|
||||
#### 条件构造器
|
||||
|
||||
除了新增以外,修改、删除、查询的SQL语句都需要指定where条件。因此BaseMapper中提供的相关方法除了以`id`作为`where`条件以外,还支持更加复杂的`where`条件。
|
||||
|
||||
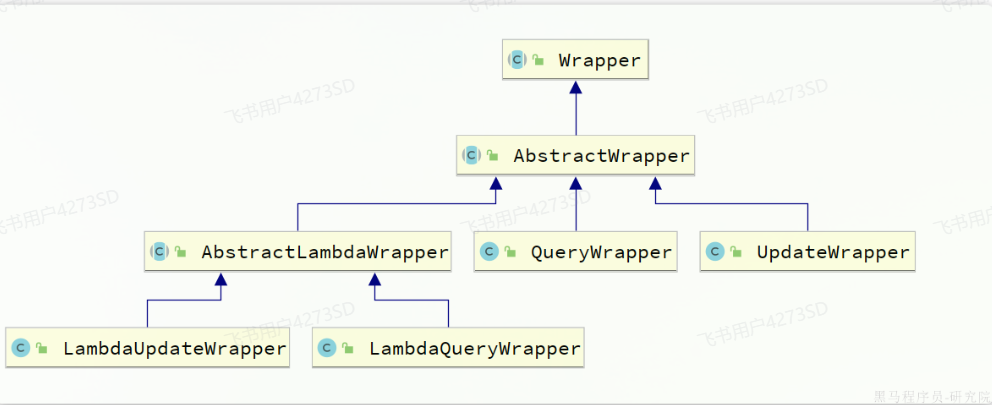
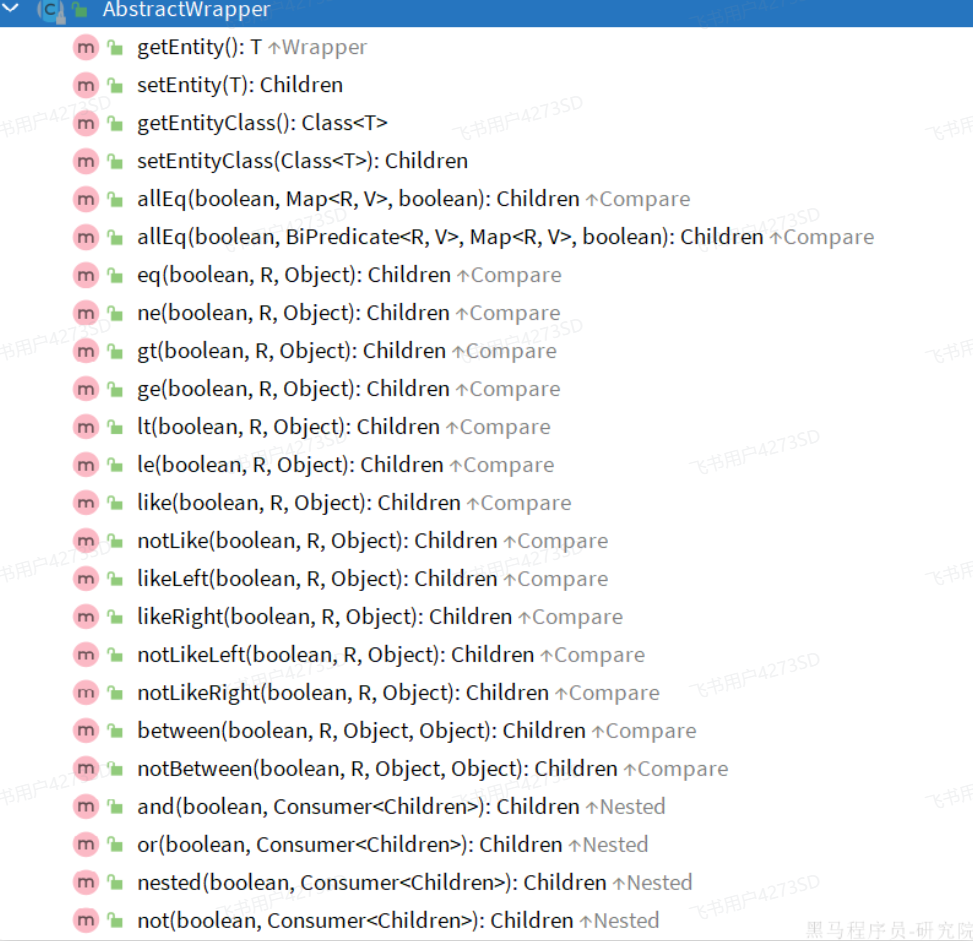
`Wrapper`就是条件构造的抽象类,其下有很多默认实现,继承关系如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**QueryWrapper**
|
||||
|
||||
```text
|
||||
/**查询出名字中带o的,存款大于等于1000元的人的id,username,info,balance
|
||||
* SELECT id,username,info,balance
|
||||
* FROM user
|
||||
* WHERE username LIKE ? AND balance >=?
|
||||
*/
|
||||
@Test
|
||||
void testQueryWrapper(){
|
||||
QueryWrapper<User> wrapper =new QueryWrapper<User>()
|
||||
.select("id","username","info","balance")
|
||||
.like("username","o")
|
||||
.ge("balance",1000);
|
||||
//查询
|
||||
List<User> users=userMapper.selectList(wrapper);
|
||||
users.forEach(System.out::println);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
```text
|
||||
//更新用户名为jack的用户的余额为2000
|
||||
@Test
|
||||
void testUpdateByQueryWrapper() {
|
||||
// 1.构建查询条件 where name = "Jack"
|
||||
QueryWrapper<User> wrapper = new QueryWrapper<User>().eq("username", "Jack");
|
||||
// 2.更新数据,user中非null字段都会作为set语句
|
||||
User user = new User();
|
||||
user.setBalance(2000);
|
||||
userMapper.update(user, wrapper);
|
||||
}
|
||||
```
|
||||
|
||||
**UpdateWrapper**
|
||||
|
||||
基于BaseMapper中的update方法更新时只能直接赋值,对于一些复杂的需求就难以实现。 例如:更新id为`1,2,4`的用户的余额,扣200,对应的SQL应该是:
|
||||
|
||||
```Java
|
||||
UPDATE user SET balance = balance - 200 WHERE id in (1, 2, 4)
|
||||
```
|
||||
|
||||
```text
|
||||
@Test
|
||||
void testUpdateWrapper() {
|
||||
List<Long> ids = List.of(1L, 2L, 4L);
|
||||
// 1.生成SQL
|
||||
UpdateWrapper<User> wrapper = new UpdateWrapper<User>()
|
||||
.setSql("balance = balance - 200") // SET balance = balance - 200
|
||||
.in("id", ids); // WHERE id in (1, 2, 4)
|
||||
// 2.更新,注意第一个参数可以给null,也就是不填更新字段和数据,
|
||||
// 而是基于UpdateWrapper中的setSQL来更新
|
||||
userMapper.update(null, wrapper);
|
||||
}
|
||||
```
|
||||
|
||||
**LambdaQueryWrapper**
|
||||
|
||||
无论是QueryWrapper还是UpdateWrapper在构造条件的时候都需要写死字段名称,会出现字符串`魔法值`。这在编程规范中显然是不推荐的。 那怎么样才能不写字段名,又能知道字段名呢?
|
||||
|
||||
其中一种办法是基于变量的`gettter`方法结合反射技术。因此我们只要将条件对应的字段的`getter`方法传递给MybatisPlus,它就能计算出对应的变量名了。而传递方法可以使用JDK8中的`方法引用`和`Lambda`表达式。 因此MybatisPlus又提供了一套基于Lambda的Wrapper,包含两个:
|
||||
|
||||
- LambdaQueryWrapper
|
||||
- LambdaUpdateWrapper
|
||||
|
||||
```text
|
||||
@Test
|
||||
void testLambdaQueryWrapper() {
|
||||
// 1.构建条件 WHERE username LIKE "%o%" AND balance >= 1000
|
||||
QueryWrapper<User> wrapper = new QueryWrapper<>();
|
||||
wrapper.lambda()
|
||||
.select(User::getId, User::getUsername, User::getInfo, User::getBalance)
|
||||
.like(User::getUsername, "o")
|
||||
.ge(User::getBalance, 1000);
|
||||
// 2.查询
|
||||
List<User> users = userMapper.selectList(wrapper);
|
||||
users.forEach(System.out::println);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**总之,推荐使用LambdaQueryWrapper,若要使用set,才用LambdaUpdateWrapper。普通的QueryWrapper用得少**
|
||||
|
||||
|
||||
|
||||
#### 自定义sql
|
||||
|
||||
可以让我们利用Wrapper生成查询条件,再结合Mapper.xml编写SQL
|
||||
|
||||
1.先在业务层利用wrapper创建条件,传递参数
|
||||
|
||||
```text
|
||||
@Test
|
||||
void testCustomWrapper() {
|
||||
// 1.准备自定义查询条件
|
||||
List<Long> ids = List.of(1L, 2L, 4L);
|
||||
QueryWrapper<User> wrapper = new QueryWrapper<User>().in("id", ids);
|
||||
|
||||
// 2.调用mapper的自定义方法,直接传递Wrapper
|
||||
userMapper.deductBalanceByIds(200, wrapper);
|
||||
}
|
||||
```
|
||||
|
||||
2. 自定义mapper层把wrapper和其他业务参数传进去,自定义sql语句书写sql的前半部分,后面拼接。
|
||||
|
||||
```text
|
||||
package com.itheima.mp.mapper;
|
||||
|
||||
import com.baomidou.mybatisplus.core.mapper.BaseMapper;
|
||||
import com.itheima.mp.domain.po.User;
|
||||
import org.apache.ibatis.annotations.Param;
|
||||
import org.apache.ibatis.annotations.Update;
|
||||
import org.apache.ibatis.annotations.Param;
|
||||
|
||||
public interface UserMapper extends BaseMapper<User> {
|
||||
@Select("UPDATE user SET balance = balance - #{money} ${ew.customSqlSegment}")
|
||||
void deductBalanceByIds(@Param("money") int money, @Param("ew") QueryWrapper<User> wrapper);
|
||||
}
|
||||
```
|
||||
|
||||
这里wrapper前面必须写@Param("ew")
|
||||
|
||||
${ew.customSqlSegment}可以自动拼接前面写的条件语句
|
||||
|
||||
|
||||
|
||||
#### Mapper层常用方法
|
||||
|
||||
**查询:**
|
||||
|
||||
selectById:根据主键 ID 查询单条记录。
|
||||
|
||||
selectBatchIds:根据主键 ID 批量查询记录。
|
||||
|
||||
selectOne:根据指定条件查询单条记录。
|
||||
|
||||
```text
|
||||
QueryWrapper<User> queryWrapper = new QueryWrapper<>();
|
||||
queryWrapper.eq("username", "alice");
|
||||
User user = userMapper.selectOne(queryWrapper);
|
||||
|
||||
```
|
||||
|
||||
selectList:根据指定条件查询多条记录。
|
||||
|
||||
```text
|
||||
QueryWrapper<User> queryWrapper = new QueryWrapper<>();
|
||||
queryWrapper.ge("age", 18);
|
||||
List<User> users = userMapper.selectList(queryWrapper);
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
**插入:**
|
||||
|
||||
insert:插入一条记录。
|
||||
|
||||
```text
|
||||
User user = new User();
|
||||
user.setUsername("alice");
|
||||
user.setAge(20);
|
||||
int rows = userMapper.insert(user);
|
||||
|
||||
```
|
||||
|
||||
**更新**
|
||||
|
||||
updateById:根据主键 ID 更新记录。
|
||||
|
||||
```text
|
||||
User user = new User();
|
||||
user.setId(1L);
|
||||
user.setAge(25);
|
||||
int rows = userMapper.updateById(user);
|
||||
|
||||
```
|
||||
|
||||
update:根据指定条件更新记录。
|
||||
|
||||
```text
|
||||
UpdateWrapper<User> updateWrapper = new UpdateWrapper<>();
|
||||
updateWrapper.eq("username", "alice");
|
||||
|
||||
User user = new User();
|
||||
user.setAge(30);
|
||||
|
||||
int rows = userMapper.update(user, updateWrapper);
|
||||
|
||||
```
|
||||
|
||||
**删除操作**
|
||||
|
||||
deleteById:根据主键 ID 删除记录。
|
||||
|
||||
deleteBatchIds:根据主键 ID 批量删除记录。
|
||||
|
||||
delete:根据指定条件删除记录。
|
||||
|
||||
```text
|
||||
QueryWrapper<User> queryWrapper = new QueryWrapper<>();
|
||||
queryWrapper.eq("username", "alice");
|
||||
|
||||
int rows = userMapper.delete(queryWrapper);
|
||||
|
||||
```
|
||||
|
||||
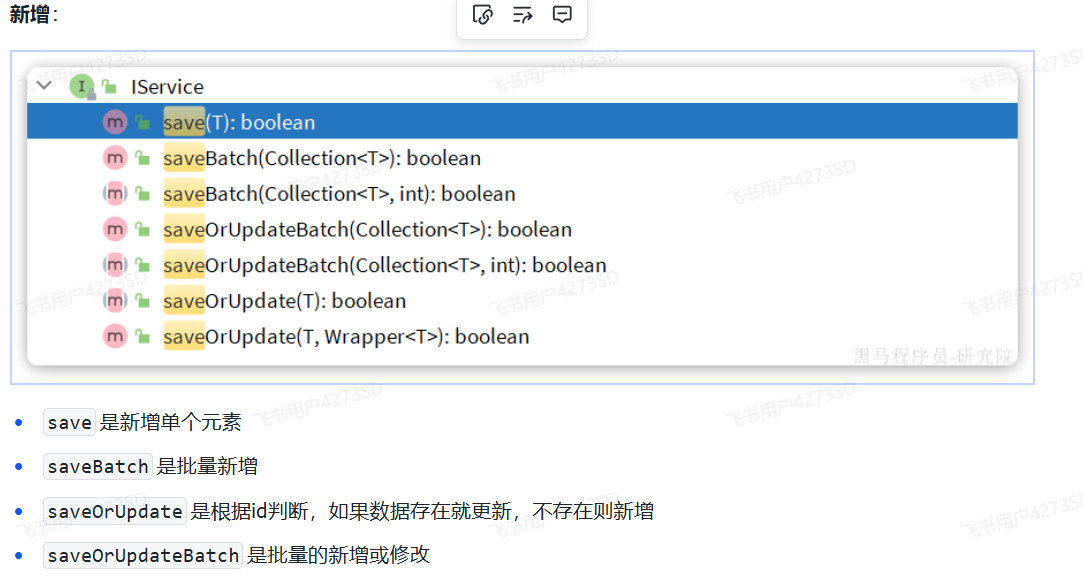
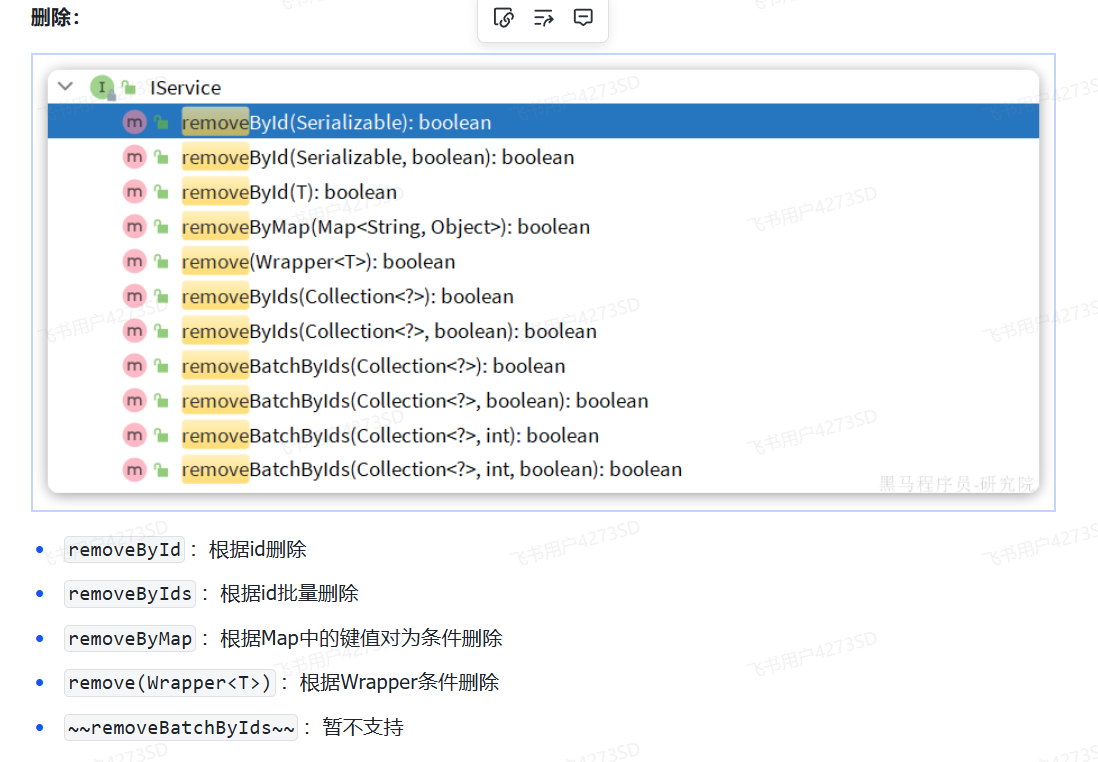
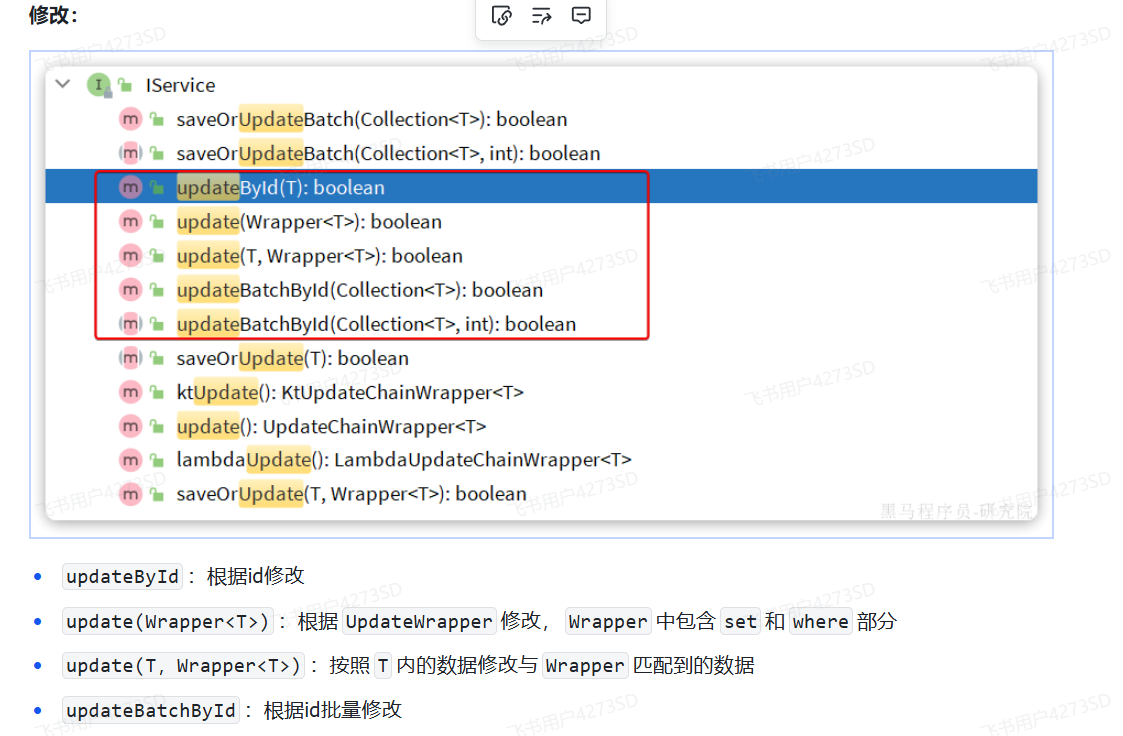
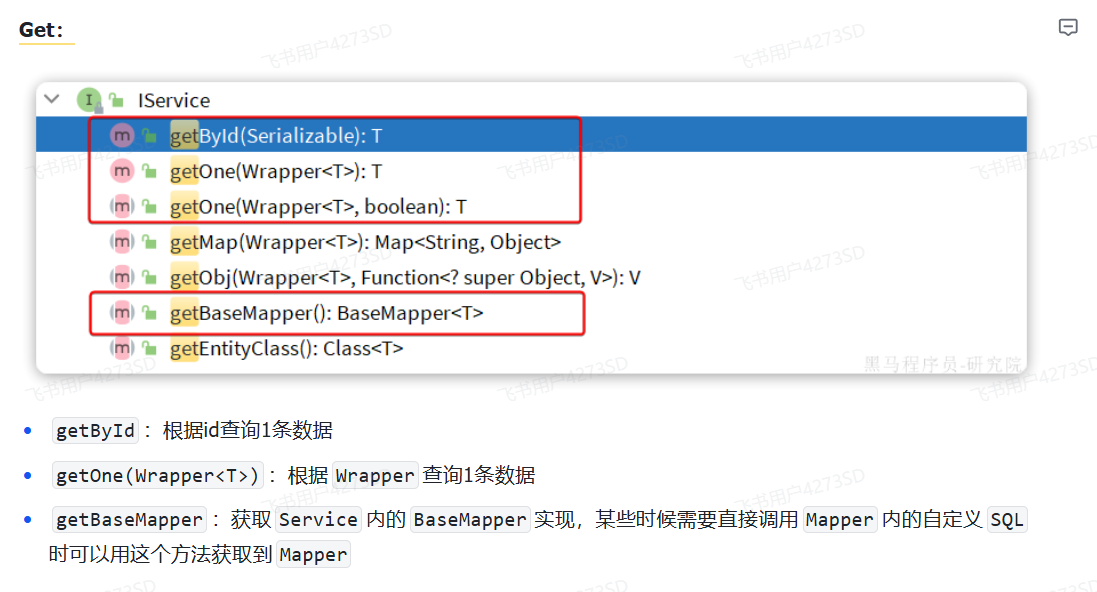
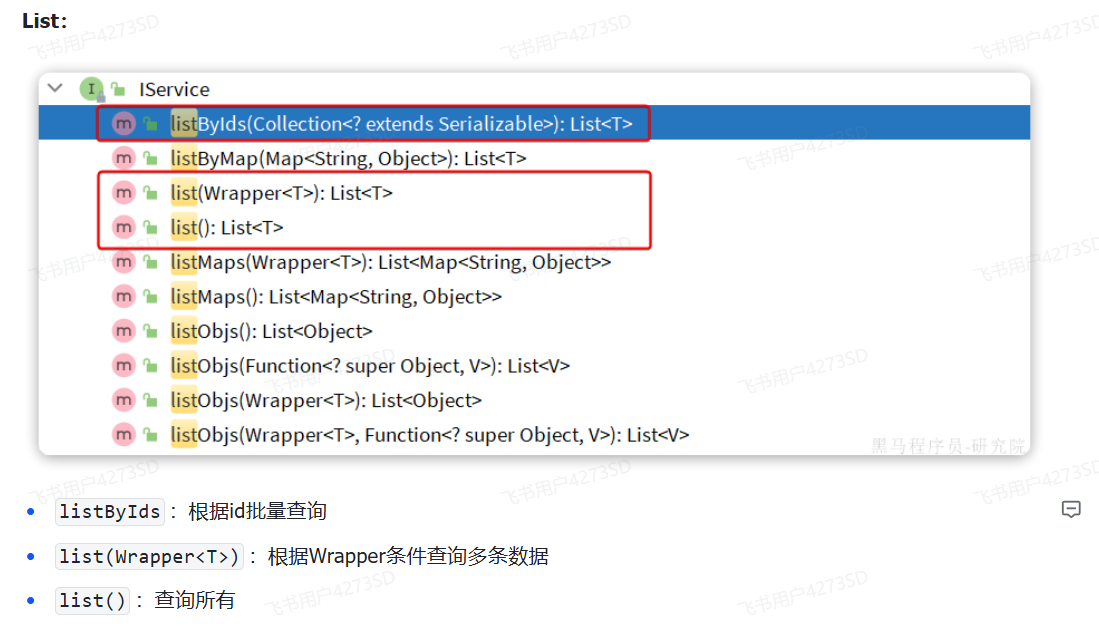
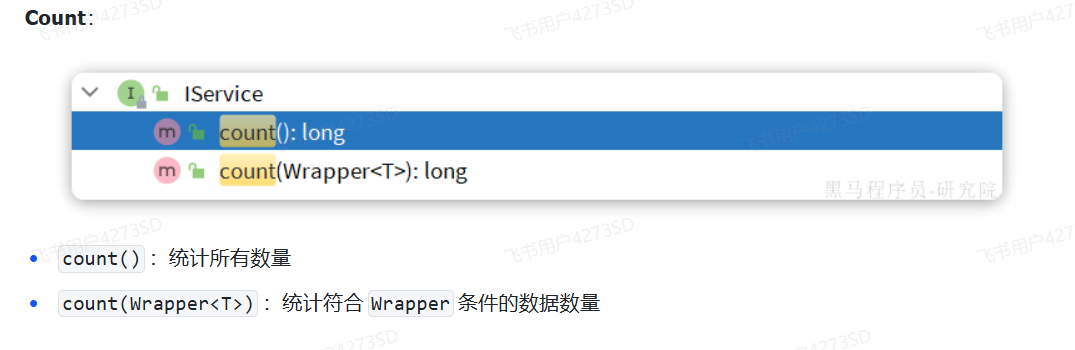
#### IService
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
由于`Service`中经常需要定义与业务有关的自定义方法,因此我们不能直接使用`IService`,而是自定义`Service`接口,然后继承`IService`以拓展方法。同时,让自定义的`Service实现类`继承`ServiceImpl`,这样就不用自己实现`IService`中的接口了。
|
||||
|
||||
首先,定义`IUserService`,继承`IService`:
|
||||
|
||||
```text
|
||||
package com.itheima.mp.service;
|
||||
|
||||
import com.baomidou.mybatisplus.extension.service.IService;
|
||||
import com.itheima.mp.domain.po.User;
|
||||
|
||||
public interface IUserService extends IService<User> {
|
||||
// 拓展自定义方法
|
||||
}
|
||||
```
|
||||
|
||||
然后,编写`UserServiceImpl`类,继承`ServiceImpl`,实现`UserService`:
|
||||
|
||||
```text
|
||||
package com.itheima.mp.service.impl;
|
||||
|
||||
import com.baomidou.mybatisplus.extension.service.impl.ServiceImpl;
|
||||
import com.itheima.mp.domain.po.User;
|
||||
import com.itheima.mp.domain.po.service.IUserService;
|
||||
import com.itheima.mp.mapper.UserMapper;
|
||||
import org.springframework.stereotype.Service;
|
||||
|
||||
@Service
|
||||
public class UserServiceImpl extends ServiceImpl<UserMapper, User>
|
||||
implements IUserService {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
2.配置service窗口,以显示多个微服务启动类
|
||||
|
||||
126
自学/苍穹外卖.md
126
自学/苍穹外卖.md
@ -489,12 +489,26 @@ public class EmployeeController {
|
||||
|
||||
**打包方式:**
|
||||
|
||||
1.*直接对父工程执行mvn clean install
|
||||
1.直接对父工程执行mvn clean install
|
||||
|
||||
2.分别对子模块common和pojo执行install,再对server执行package
|
||||
|
||||
因为Maven 在构建 `sky-server` 时,去你本地仓库或远程仓库寻找它依赖的两个 SNAPSHOT 包。
|
||||
|
||||
在父工程的pom中添加这段,能将你的应用和所有依赖都打到一个可执行的 “fat jar” 里
|
||||
|
||||
```xml
|
||||
<build>
|
||||
<finalName>${project.artifactId}</finalName>
|
||||
<plugins>
|
||||
<plugin>
|
||||
<groupId>org.springframework.boot</groupId>
|
||||
<artifactId>spring-boot-maven-plugin</artifactId>
|
||||
</plugin>
|
||||
</plugins>
|
||||
</build>
|
||||
```
|
||||
|
||||
**JAVA项目dockerfile:**
|
||||
|
||||
```dockerfile
|
||||
@ -531,6 +545,7 @@ Spring Boot 的启动器会:
|
||||
|
||||
```yml
|
||||
version: "3.8"
|
||||
|
||||
services:
|
||||
mysql:
|
||||
image: mysql:8.0
|
||||
@ -545,7 +560,9 @@ services:
|
||||
- ./init/sky.sql:/docker-entrypoint-initdb.d/sky.sql:ro
|
||||
- ./mysql-conf/my.cnf:/etc/mysql/conf.d/my.cnf:ro
|
||||
ports:
|
||||
- "3307:3306"
|
||||
- "3306:3306"
|
||||
networks:
|
||||
- sky-net
|
||||
|
||||
redis:
|
||||
image: redis:7.0-alpine
|
||||
@ -556,9 +573,10 @@ services:
|
||||
- ./data/redis:/data
|
||||
ports:
|
||||
- "6379:6379"
|
||||
networks:
|
||||
- sky-net
|
||||
|
||||
app:
|
||||
# 构建并打标签 sky-server:latest
|
||||
build:
|
||||
context: .
|
||||
dockerfile: Dockerfile
|
||||
@ -567,20 +585,24 @@ services:
|
||||
depends_on:
|
||||
- mysql
|
||||
- redis
|
||||
# 挂载敏感配置到 /app/config
|
||||
volumes:
|
||||
- ./config:/app/config:ro
|
||||
environment:
|
||||
TZ: Asia/Shanghai
|
||||
# 激活 dev 配置文件:application-dev.yml
|
||||
SPRING_PROFILES_ACTIVE: dev
|
||||
ports:
|
||||
- "8085:8085"
|
||||
restart: always
|
||||
networks:
|
||||
- sky-net
|
||||
|
||||
volumes:
|
||||
mysql:
|
||||
redis:
|
||||
|
||||
networks:
|
||||
sky-net:
|
||||
external: true
|
||||
```
|
||||
|
||||
**其中启动数据库要准备两份文件:**
|
||||
@ -616,13 +638,80 @@ Docker Compose 里的 `environment:` 无法读取`application-dev.yml`,要不
|
||||
|
||||
### 滚动开发阶段
|
||||
|
||||
1.仅需改动Dokcerfile,docker-compose无需更改:
|
||||
|
||||
```dockerfile
|
||||
# —— 第一阶段:Maven 构建 ——
|
||||
FROM maven:3.8.7-eclipse-temurin-17-alpine AS builder
|
||||
WORKDIR /workspace
|
||||
|
||||
# 把项目级 settings.xml 复制到容器里
|
||||
COPY .mvn/settings.xml /root/.m2/settings.xml
|
||||
|
||||
# 1) 先把父 POM 和所有子模块的目录结构都复制过来
|
||||
COPY whut-take-out-backend/pom.xml ./pom.xml
|
||||
COPY whut-take-out-backend/sky-common ./sky-common
|
||||
COPY whut-take-out-backend/sky-pojo ./sky-pojo
|
||||
COPY whut-take-out-backend/sky-server ./sky-server
|
||||
|
||||
# (可选:如果父 pom 有 <modules>,也可把 settings.xml、父级的其它 POM 拷过来)
|
||||
RUN mvn dependency:go-offline -B
|
||||
|
||||
# 2) 拷贝所有子模块源码
|
||||
COPY whut-take-out-backend ./whut-take-out-backend
|
||||
|
||||
# 3) 只构建 sky-server 模块(并且把依赖模块一并编译)
|
||||
RUN mvn -f whut-take-out-backend/pom.xml clean package \
|
||||
-pl sky-server -am \
|
||||
-DskipTests -B
|
||||
|
||||
# —— 第二阶段:运行时镜像 ——
|
||||
FROM openjdk:17-jdk-slim
|
||||
ENV TZ=Asia/Shanghai
|
||||
RUN ln -snf /usr/share/zoneinfo/$TZ /etc/localtime && echo $TZ > /etc/timezone
|
||||
|
||||
WORKDIR /app
|
||||
# 4) 把第一阶段产物(sky-server 模块的 Jar)拷过来
|
||||
COPY --from=builder \
|
||||
/workspace/whut-take-out-backend/sky-server/target/sky-server-*.jar \
|
||||
./app.jar
|
||||
|
||||
EXPOSE 8085
|
||||
ENTRYPOINT ["java", "-jar", "app.jar"]
|
||||
|
||||
```
|
||||
|
||||
2.maven构建依赖可能比较慢,需创建.mvn/settings.xml
|
||||
|
||||
```xml
|
||||
<settings xmlns="http://maven.apache.org/SETTINGS/1.1.0"
|
||||
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
|
||||
xsi:schemaLocation="http://maven.apache.org/SETTINGS/1.1.0
|
||||
https://maven.apache.org/xsd/settings-1.1.0.xsd">
|
||||
<mirrors>
|
||||
<mirror>
|
||||
<id>aliyun</id>
|
||||
<name>aliyun maven</name>
|
||||
<url>https://maven.aliyun.com/repository/public</url>
|
||||
<mirrorOf>central,apache.snapshots</mirrorOf>
|
||||
</mirror>
|
||||
</mirrors>
|
||||
</settings>
|
||||
```
|
||||
|
||||
使用阿里云镜像加速
|
||||
|
||||
3.验证:http://124.71.159.195:8085/doc.html
|
||||
|
||||
|
||||
|
||||
## 前端部署
|
||||
|
||||
直接部署开发完毕的前端代码,准备:
|
||||
|
||||
1.静态资源html文件夹
|
||||
0.创建docker网络:`docker network create sky-net`
|
||||
|
||||
1.静态资源html文件夹(npm run build 打包源码获得)
|
||||
|
||||
2.nginx.conf
|
||||
|
||||
@ -636,6 +725,31 @@ upstream webservers {
|
||||
}
|
||||
```
|
||||
|
||||
因为同一个网络下的服务名会自动注册DNS,进行地址解析!
|
||||
|
||||
3.docker-compose文件
|
||||
|
||||
```yml
|
||||
version: "3.8"
|
||||
services:
|
||||
frontend:
|
||||
image: nginx:alpine
|
||||
container_name: sky-frontend
|
||||
ports:
|
||||
- "85:80"
|
||||
volumes:
|
||||
# 把本地 html 目录挂到容器的默认站点目录
|
||||
- ./html:/usr/share/nginx/html:ro
|
||||
# 把本地的 nginx.conf 覆盖容器里的配置
|
||||
- ./nginx.conf:/etc/nginx/nginx.conf:ro
|
||||
networks:
|
||||
- sky-net
|
||||
|
||||
networks:
|
||||
sky-net:
|
||||
external: true
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 实战开发
|
||||
|
||||
92
自学/草稿.md
92
自学/草稿.md
@ -1,70 +1,44 @@
|
||||
下面是 Java 中 `java.util.Random` 类的简要介绍及几种最常用的用法示例。
|
||||
主要区别在于它们的**用途**和**能执行的操作**不同:
|
||||
|
||||
| 特性 | `lambdaQuery()` | `lambdaUpdate()` |
|
||||
| -------------- | --------------------------------------------------------- | --------------------------------------------------------- |
|
||||
| **主要用途** | 构造查询条件,执行 `SELECT` 操作 | 构造更新条件,执行 `UPDATE`(或逻辑删除)操作 |
|
||||
| **返回类型** | `LambdaQueryChainWrapper<T>` 或 `LambdaQueryWrapper<T>` | `LambdaUpdateChainWrapper<T>` 或 `LambdaUpdateWrapper<T>` |
|
||||
| **支持的方法** | `.eq()`, `.like()`, `.gt()`, `.orderBy()`, `.select()` 等 | `.eq()`, `.lt()`, `.set()`, `.setSql()` 等 |
|
||||
| **执行方法** | `.list()`, `.one()`, `.page()` 等 | `.update()`, `.remove()`(逻辑删除) |
|
||||
|
||||
------
|
||||
|
||||
## 1. 基本概念
|
||||
### 举例对比
|
||||
|
||||
- `Random` 是伪随机数生成器,内部用线性同余法(LCG)产生序列。
|
||||
- 如果不传 seed,默认以当前时间作为种子;传入相同 seed 会得到相同的“随机”序列,方便测试。
|
||||
1. **查询:`lambdaQuery()`**
|
||||
|
||||
```java
|
||||
import java.util.Random;
|
||||
```java
|
||||
// 查出状态为 1,名字中含 “张”,并按年龄降序的前 10 条用户
|
||||
List<User> list = userService.lambdaQuery()
|
||||
.eq(User::getStatus, 1)
|
||||
.like(User::getName, "张")
|
||||
.orderByDesc(User::getAge)
|
||||
.last("LIMIT 10")
|
||||
.list();
|
||||
```
|
||||
|
||||
Random rnd1 = new Random(); // 随机种子
|
||||
Random rnd2 = new Random(12345L); // 固定种子 -> 每次结果相同
|
||||
```
|
||||
2. **更新:`lambdaUpdate()`**
|
||||
|
||||
```java
|
||||
// 把状态为 0,且注册时间超过两年的用户标记为状态 2
|
||||
boolean ok = userService.lambdaUpdate()
|
||||
.eq(User::getStatus, 0)
|
||||
.lt(User::getRegisterTime, LocalDate.now().minusYears(2))
|
||||
.set(User::getStatus, 2)
|
||||
.update();
|
||||
```
|
||||
|
||||
------
|
||||
|
||||
## 2. 常用方法
|
||||
#### 小结
|
||||
|
||||
| 方法 | 功能 | 返回值范围 |
|
||||
| ---------------- | ----------------------- | ----------------------------------------- |
|
||||
| `nextInt()` | 任意 int | `Integer.MIN_VALUE` … `Integer.MAX_VALUE` |
|
||||
| `nextInt(bound)` | 0(含)至 bound(不含) | `[0, bound)` |
|
||||
| `nextLong()` | 任意 long | 整个 long 范围 |
|
||||
| `nextDouble()` | double 小数 | `[0.0, 1.0)` |
|
||||
| `nextBoolean()` | 布尔值 | `true` 或 `false` |
|
||||
| `nextGaussian()` | 高斯(正态)分布 | 均值 0、标准差 1 |
|
||||
- 用 `lambdaQuery()` 构造查询条件,只做 **读** 操作。
|
||||
- 用 `lambdaUpdate()` 构造更新条件,结合 `.set()` 指定要修改的字段,做 **改**(或 “逻辑删”)操作。
|
||||
|
||||
------
|
||||
|
||||
## 3. 示例代码
|
||||
|
||||
```java
|
||||
import java.util.Random;
|
||||
import java.util.stream.IntStream;
|
||||
|
||||
public class RandomDemo {
|
||||
public static void main(String[] args) {
|
||||
Random rnd = new Random(); // 随机种子
|
||||
Random seeded = new Random(2025L); // 固定种子
|
||||
|
||||
// 1) 随机整数
|
||||
int a = rnd.nextInt(); // 任意 int
|
||||
int b = rnd.nextInt(100); // [0,100)
|
||||
System.out.println("a=" + a + ", b=" + b);
|
||||
|
||||
// 2) 随机浮点数与布尔
|
||||
double d = rnd.nextDouble(); // [0.0,1.0)
|
||||
boolean flag = rnd.nextBoolean();
|
||||
System.out.println("d=" + d + ", flag=" + flag);
|
||||
|
||||
// 3) 高斯分布
|
||||
double g = rnd.nextGaussian(); // 均值0,σ=1
|
||||
System.out.println("gaussian=" + g);
|
||||
|
||||
// 4) 生成一组随机数流
|
||||
IntStream stream = rnd.ints(5, 50, 60); // 5 个 [50,60) 的随机 ints
|
||||
System.out.print("stream: ");
|
||||
stream.forEach(n -> System.out.print(n + " "));
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
------
|
||||
|
||||
## 4. 小贴士
|
||||
|
||||
- 并发环境下可用 `ThreadLocalRandom.current()`,避免多线程竞争。
|
||||
- 若只需加密强度随机数,请使用 `SecureRandom`。
|
||||
它们都是为了解决写 SQL 时硬编码字段名的问题,通过 `User::getXxx` 方法引用,保证 **类型安全**、**重构无忧**。
|
||||
Loading…
x
Reference in New Issue
Block a user