Commit on 2025/04/15 周二 12:46:07.77

2025-04-15 12:46:07 +08:00 · 2025-04-15 12:46:07 +08:00 · e9e0a05fe4
commit e9e0a05fe4
parent ef468a3e46
10 changed files with 458 additions and 129 deletions
--- a/科研/循环神经网络.md
+++ b/科研/循环神经网络.md
@ -218,7 +218,7 @@ LSTM 的核心在于其“细胞状态”（cell state），这是一个贯穿

 ### 隐藏状态更新公式

-对于每个时间步 $t$，LSTM 的更新过程通常可以写为以下公式（所有权重矩阵用 $W$ 和 $U$ 表示，各门的偏置为 $b$）：
+对于**每个时间步** $t$，LSTM 的更新过程通常可以写为以下公式（所有权重矩阵用 $W$ 和 $U$ 表示，各门的偏置为 $b$）：

 $$
 \begin{aligned}
@ -231,11 +231,20 @@ $$
 \end{aligned}
 $$

+**连续传递**  
+
+在时间步 $t$ 中计算出的隐藏状态 $h_t$ 会作为下一时间步 $t+1$ 的输入之一，与当前输入 $x_{t+1}$ 一起用于后续计算。这样，每个 $h_t$ 都包含了前面所有时间步的信息，从而实现信息的传递和累积。
+
+**最终输出预测**  
+
+如果任务是做序列到单个输出（例如分类、回归等），通常最后一个时间步（即 $h_T$）会用作整个序列的表示，并作为最终的特征传递给预测层（如全连接层）进行输出预测。但需要注意的是，在一些任务中，比如序列标注或序列生成，每个时间步的隐藏状态都可能参与输出预测或进一步处理。

 ### 直观理解

 - **细胞状态 $c_t$**：  
  细胞状态是贯穿整个序列的“记忆通道”，负责长期保存信息。它像一条传送带，在不同时间步中线性传递，避免信息被频繁修改，**从而维持长期记忆**。
+- **隐藏状态$h_t$**：
+  代表的是当前时间步的输出或者说是短时记忆。它是基于当前输入以及细胞状态经过非线性激活处理后的结果，反映了对当前时刻输入信息的即时响应。
 - **遗忘门 $f_t$**：  
  用于丢弃上一时刻不再需要的信息。如果遗忘门输出接近 0，说明遗忘了大部分过去的信息；如果接近 1，则保留大部分信息。
  **类比**：若模型遇到新段落，遗忘门可能关闭（输出接近0），丢弃前一段的无关信息；若需要延续上下文（如故事主线），则保持开启（输出接近1）。
@ -243,12 +252,27 @@ $$
  输入门控制有多少候选信息被写入细胞状态。候选细胞状态是基于当前输入和上一时刻隐藏状态生成的新信息。
  **类比**：阅读时遇到关键情节，输入门打开，将新信息写入长期记忆（如角色关系），同时候选状态  $\tilde{c}_t$提供新信息的候选内容。

-
-
 - **输出门 $o_t$**：  
  控制从细胞状态中输出多少信息作为当前时间步的隐藏状态。隐藏状态 $h_t$ 通常用于后续计算（例如，生成输出、参与下一时刻计算）。
  **类比**：根据当前任务（如预测下一个词），输出门决定暴露细胞状态的哪部分（如只关注时间、地点等关键信息）。

+### 双层或多层LSTM
+
+双层 LSTM 是指将两个 LSTM 层堆叠在一起：  
+
+- **第一层 LSTM**  
+  处理输入序列 $x_1, x_2, \ldots, x_T$ 后，生成每个时间步的隐藏状态 $h_t^{(1)}$。  
+- **第二层 LSTM**  
+  以第一层输出的隐藏状态序列 $\{h_1^{(1)}, h_2^{(1)}, \ldots, h_T^{(1)}\}$ 作为输入，进一步计算新的隐藏状态 $h_t^{(2)}$。  
+
+作用与优势：
+
+- **捕捉更复杂的模式**  
+  - 第一层：提取低层次特征（如局部变化、短时依赖）。  
+  - 第二层：整合低层特征，捕捉长距离依赖或抽象模式。  
+- **更强的表达能力**  
+  通过多层堆叠，网络能建模更复杂的序列数据映射关系。
+


 ## 时序卷积网络TCN
--- a/科研/数学基础.md
+++ b/科研/数学基础.md
@ -570,6 +570,8 @@ $$
 - x 在 μ-2σ 和 μ+2σ 之间的样本数量占到整个样本数量的 95.4%；
 - x 在 μ-3σ 和 μ+3σ 之间的样本数量占到整个样本数量的99.6%；

+
+
 ## 数据融合

 当前最优值=当前的先验估计值和观测值进行融合
@ -578,6 +580,8 @@ $$

 ![image-20240311132453071](https://pic.bitday.top/i/2025/03/19/u8dbq1-2.png)

+
+
 ## 拉普拉斯变换

 ### 拉普拉斯变换的定义
@ -617,16 +621,6 @@ $$



-## 幂迭代
-
-![image-20240428174019083](https://pic.bitday.top/i/2025/03/19/u8ecqs-2.png)
-
-![image-20240428173732285](https://pic.bitday.top/i/2025/03/19/u8ekvp-2.png)
-
-原理：每一次迭代都相当于将当前向量乘以 $A$ 后再归一化。由于矩阵 $A$ 作用下，初始向量中 $v_1$ 分量对应的系数**会按 $\lambda_1$ 的 $k$ 次幂**增长，而其他特征向量分量增长较慢（因为它们对应的特征值模较小），故随着迭代次数的增加，向量逐渐趋向于 $v_1$ 的方向。
-
-
-
 ## 拉普拉斯矩阵

 ### **拉普拉斯矩阵及其性质**
@ -1151,3 +1145,37 @@ $$



+## 幂迭代
+
+幂迭代方法是一种常用的数值迭代算法，主要用于计算矩阵的**主特征值**（即具有最大模长的特征值）及其对应的**特征向量**。
+
+**收敛原理**
+
+在多数实际问题中，矩阵的特征值中存在一个绝对值最大的特征值。根据线性代数理论：
+
+- 任取一个非零初始向量（且在主特征向量方向上的分量不为0）
+- 通过不断与矩阵相乘并归一化，该向量会逐渐趋近于主特征向量方向
+- 其他较小特征值对应的分量会被逐渐"削弱"
+
+**算法步骤**
+
+1. **选取初始向量**  
+   选择非零初始向量 $$x^{(0)}$$
+
+2. **迭代更新**  
+   每次迭代计算：
+   $$
+   x^{(k+1)} = A x^{(k)}
+   $$
+   并进行二范数归一化以保持数值稳定性
+
+3. **收敛判断**  
+   当相邻迭代向量足够接近时停止，此时：
+
+   - 归一化向量 ≈ 主特征向量
+
+   - 特征值估计：
+     $$
+     \lambda^{(k)} = \frac{(x^{(k)})^T A x^{(k)}}{(x^{(k)})^T x^{(k)}}
+     $$
+
--- a/科研/李雅普诺夫稳定性.md
+++ b/科研/李雅普诺夫稳定性.md
@ -28,24 +28,6 @@



-**特征值、特征向量的几何意义**
-
-![image-20240413162816588](https://pic.bitday.top/i/2025/03/19/u8hmgh-2.png)
-
-矩阵A表示某线性变换
-
-
-
-![image-20240413163625587](https://pic.bitday.top/i/2025/03/19/u8i8s1-2.png)
-
-<img src="https://pic.bitday.top/i/2025/03/19/u8matf-2.png" alt="image-20240413165536752" style="zoom:50%;" />
-
-<img src="https://pic.bitday.top/i/2025/03/19/u8jxu7-2.png" alt="image-20240413165512450" style="zoom:50%;" />
-
-为结论
-
-
-
 ## 稳定性的定义

 ![微信图片_20240413101222](https://pic.bitday.top/i/2025/03/19/u8m4zk-2.png)
--- a/科研/草稿.md
+++ b/科研/草稿.md
@ -1,67 +1 @@
-这里涉及到的是神经网络中常用的全连接层（dense layer）的矩阵乘法约定，不同的表示方式会有不同的矩阵尺寸和乘法顺序，下面给出两种常见的约定，并解释如何让维度匹配：
-
---
-
-### 方法一：以行向量表示输入
-
-1. **设定输入为行向量：**  
-   假设每个节点的隐藏状态由 LSTM 输出后表示为一个行向量，即  
-   $$
-   h_i \in \mathbb{R}^{1 \times d''}
-   $$
-   这里 $d''$ 是 LSTM 隐藏单元的数量。
-
-2. **全连接层权重矩阵：**  
-   为了将行向量 $h_i$ 映射到预测的二维坐标，设计全连接层的权重矩阵 $W_{\text{fc}}$ 的尺寸为  
-   $$
-   W_{\text{fc}} \in \mathbb{R}^{d'' \times 2}
-   $$
-   这样，乘法操作 $h_i \cdot W_{\text{fc}}$ 的计算是：
-   - $h_i$ 的尺寸：$1 \times d''$
-   - $W_{\text{fc}}$ 的尺寸：$d'' \times 2$
-   - 相乘结果：$1 \times 2$
-
-3. **加偏置得到最终输出：**  
-   同时，全连接层有一个偏置向量 $b_{\text{fc}} \in \mathbb{R}^{1 \times 2}$，故有  
-   $$
-   \hat{y}_i = h_i \cdot W_{\text{fc}} + b_{\text{fc}} \in \mathbb{R}^{1 \times 2},
-   $$
-   表示该节点预测的二维坐标 $(x, y)$。
-
---
-
-### 方法二：以列向量表示输入
-
-1. **设定输入为列向量：**  
-   如果我们将每个节点的隐藏状态表示为列向量：  
-   $$
-   h_i \in \mathbb{R}^{d'' \times 1},
-   $$
-   则需要调整矩阵乘法的顺序。
-
-2. **全连接层权重矩阵：**  
-   此时全连接层的权重矩阵应设置为  
-   $$
-   W_{\text{fc}} \in \mathbb{R}^{2 \times d''},
-   $$
-   这样通过矩阵乘法：  
-   $$
-   \hat{y}_i = W_{\text{fc}} \cdot h_i + b_{\text{fc}},
-   $$
-   - $W_{\text{fc}}$ 的尺寸：$2 \times d''$
-   - $h_i$ 的尺寸：$d'' \times 1$
-   - 乘积结果为：$2 \times 1$
-   
-   对应的偏置 $b_{\text{fc}} \in \mathbb{R}^{2 \times 1}$ 后，最终输出为 $2 \times 1$（可以看作二维坐标）。
-
---
-
-### 总结说明
-
- **两种约定等价：**  
-  实际实现时，只要保持输入和权重矩阵的乘法顺序一致，确保内维度匹配，输出最终都会是一个二维向量。在深度学习框架中（例如 Keras 或 PyTorch），通常默认每个样本以行向量形式表示（形状为 $(\text{batch\_size}, d'')$），因此全连接层权重设置为 $(d'', 2)$，计算 $h \cdot W$ 会得到形状为 $(\text{batch\_size}, 2)$ 的输出。
-
- **回答疑问：**  
-  “你这里 $W$ 和 $h$ 怎么能矩阵乘法呢”——关键在于你要统一向量的表示方式。如果你使用行向量表示每个节点，则 $h$ 的维度是 $1 \times d''$；对应的全连接层权重 $W_{\text{fc}}$ 为 $d'' \times 2$。这样乘法 $h \cdot W_{\text{fc}}$ 内维度 $d''$ 正好匹配，输出得到 $1 \times 2$ 的向量。如果反之使用列向量表示，则需要调整权重矩阵为 $2 \times d''$ 并将乘法表达为 $W_{\text{fc}} \cdot h$。
-
-W_{\text{fc}} \in \mathbb{R}^{2 \times d''}
+压缩感知   函数拟合  采样定理  傅里叶变换
--- a/科研/陈茂森论文.md
+++ b/科研/陈茂森论文.md
@ -0,0 +1,217 @@
+# 陈茂森论文
+
+## 随机移动网络系统的稳定性
+
+### 马尔科夫链与网络平均度推导
+
+**1.马尔科夫链的基本概念**
+
+马尔科夫链描述的是这样一种随机过程：系统在若干个可能的状态中变化，**下一时刻所处状态只依赖于当前状态**，而与过去的状态无关，这就是所谓的“无记忆性”或**马尔科夫性**。
+
+**无记忆性**意味着，对于任何 $s, t \ge 0$，
+$$
+P(T > s+t \mid T > s) = P(T > t).
+$$
+
+假设你已经等待了 $s$ 分钟，那么再等待至少 $t$ 分钟的概率，和你一开始就等待至少 $t$ 分钟的概率完全相同。
+
+
+
+在这个模型中，每条链路只有两个可能的状态：
+
+- **状态0**：链路断开
+- **状态1**：链路连通
+
+设在时刻 $t$ 时，某条链路处于连通状态的概率为 $p_1(t)$；由于只有两种状态，所以断开的概率就是  
+$$
+p_0(t)=1-p_1(t).
+$$
+
+同时，我们假设链路从一个状态转移到另一个状态需要等待一段时间，这段**等待时间**通常服从**指数分布**（论文中通过 KS 检验确认）。这意味着，从0到1和从1到0有两个转移速率，我们记作：
+
+- 从0到1的转移速率为 $\lambda_{01}$  
+- 从1到0的转移速率为 $\lambda_{10}$
+
+这些速率表示单位时间内发生状态转换的可能性。
+
+**2.推导单条链路的连通概率**
+
+根据连续时间马尔科夫链的理论，我们可以写出**状态转移的微分方程**。对于状态1（连通状态），概率 $p_1(t)$ 的变化率由两个部分组成：
+
+1. 当链路处于状态0时，以速率 $\lambda_{01}$ 变为状态1。这部分概率增加的速率为  
+   $$
+   \lambda_{01} \, p_0(t)=\lambda_{01} (1-p_1(t)).
+   $$
+
+2. 当链路处于状态1时，以速率 $\lambda_{10}$ 转换为状态0。这部分使 $p_1(t)$ 减少，其速率为  
+   $$
+   \lambda_{10} \, p_1(t).
+   $$
+
+所以，$p_1(t)$ 的微分方程写成：
+$$
+\frac{d p_1(t)}{dt} = \lambda_{01} \, (1-p_1(t)) - \lambda_{10} \, p_1(t).
+$$
+
+这个方程可以整理为：
+$$
+\frac{d p_1(t)}{dt} + (\lambda_{01}+\lambda_{10}) \, p_1(t) = \lambda_{01}.
+$$
+
+这其实是一个一阶线性微分方程，其标准求解方法是求解其齐次解与非齐次解。
+
+**3. 求解微分方程**
+
+整个微分方程的通解为：
+$$
+p_1(t)= \frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}} + C\, e^{-(\lambda_{01}+\lambda_{10})t}.
+$$
+
+利用初始条件 $p_1(0)=p_1^0$（初始时刻链路连通的概率），我们可以求出 $C$：
+
+即
+$$
+C = p_1^0 -\frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}}.
+$$
+
+所以，链路在任意时刻 $t$ 连通的概率为：
+$$
+p_1(t)= \frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}} + \left( p_1^0 -\frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}} \right)e^{-(\lambda_{01}+\lambda_{10})t}.
+$$
+
+这就是单条链路的连通概率函数，描述了从任意初始条件出发，经过一段时间后，链路达到平衡状态的过程。
+
+**4.推导网络平均度的变化函数**
+
+在一个由 $N$ 个节点构成的网络中，每个节点都与其它节点进行通信（不考虑自环），因此每个节点最多有 $N-1$ 个邻居。对于任意一对节点 $i$ 和 $j$，它们之间链路连通的概率 $p_1(t)$（假设所有链路**独立且同分布**）。
+
+- 某个节点 $i$ 在时刻 $t$ 的度 $d_i(t)$可以写作：
+  $$
+  d_i(t)= \sum_{\substack{j=1 \\ j\neq i}}^N p_{ij}(t),
+  $$
+  其中 $p_{ij}(t)=p_1(t)$。
+
+- 因此，每个节点的期望度为：
+  $$
+  E[d_i(t)]=(N-1)p_1(t).
+  $$
+
+- 网络平均度就是对所有节点的期望度取平均，由于网络中每个节点都遵循相同统计规律，所以网络平均度可表示为：
+  $$
+  \bar{d}(t) = \frac{1}{N}\sum_{i=1}^{N} E[d_i(t)] = \frac{N \cdot (N-1)p_1(t)}{N} = (N-1)p_1(t)
+  $$
+
+将我们前面得到的 $p_1(t)$ 表达式代入，就得到网络平均度随时间变化的表达式：
+$$
+\bar{d}(t)= (N-1)\left[ \frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}} + \left( p_1^0 -\frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}} \right)e^{-(\lambda_{01}+\lambda_{10})t}\right].
+$$
+
+这就是**网络平均度的变化函数**：
+
+- 网络开始时每条链路的连通概率为 $p_1^0$ 
+- 这种调整过程符合指数衰减规律，即偏离平衡值的部分按 $e^{-(\lambda_{01}+\lambda_{10})t}$ 衰减
+- 当 $t$ 趋向无穷大时，指数项 $e^{-(\lambda_{01}+\lambda_{10})t}$ 衰减为0，网络平均度趋向于  $(N-1)\frac{\lambda_{01}}{\lambda_{01}+\lambda_{10}}$，这就是网络达到平衡状态后的理论平均度。
+
+
+
+### 特征信号参数的平稳性
+
+证明**系统在平衡态下具有统计上的稳定性**。
+
+#### **从节点空间分布证明平稳性。**
+
+设节点在模型区域的坐标为 $(X,Y)$，其分布概率密度函数写为
+$$
+f(x,y).
+$$
+
+那么节点在模型子区域 $R_1$ 中出现的概率为
+
+$$
+P_{R_1}=\int_{R_1} f(x,y) \,dx\,dy.
+$$
+
+在平衡状态下，理论上节点的位置分布 **$f(x,y)$ 保持不变**，即每个区域内节点出现的概率 $P_{R_1}$ 是常数，不随时间变化。证明在平衡状态下节点分布稳定。
+
+#### **扰动后的恢复能力**
+
+- 静止节点分布特性满足均匀分布,概率密度函数为 $g(x,y)$；
+- 运动节点的概率密度函数为 $h(x,y)$；
+- **在时刻 $t_0$ 时**，网络中共有 $N$ 个节点，其中有 $s$ 个静止，故**静止节点的比例为 $p=\frac{s}{N}$**。
+
+节点整体的分布概率密度函数可写为
+
+$$
+f(x,y)=p\, g(x,y)+(1-p)\, h(x,y).
+$$
+
+在平衡状态下，$p$ 的理论值为一个常数，所以 $f(x,y)$ 不随时间变化，从而网络连通度稳定。
+
+
+
+接下来，**考虑外界扰动**的影响：假设在**时刻 $t_1$** 新加入 $m$ 个**符合均匀分布的节点**，
+
+**扰动后的总分布（$t_1$时刻后）**
+
+- 新加入的 $m$ 个节点是静止的，其分布为 $g(x,y)$
+- 此时网络的总节点数 $N+m$：
+  - **静止节点总数**：$s+m$
+  - **运动节点总数**：$N-s$（原有运动节点数不变）
+
+因此，扰动后的分布为：  
+$$
+f(x,y,t_1) = \frac{s + m}{N + m} g(x,y) + \frac{N - s}{N + m} h(x,y)
+$$
+
+$$
+f(x,y,t_1) = p' \cdot g(x,y) + (1-p') \cdot h(x,y)
+$$
+
+其中 $p' = \frac{s + m}{N + m}$。
+
+**近似处理（当 $N, s \gg m$ 时）**
+$$
+p' = \frac{s + m}{N + m} \approx \frac{s}{N} = p
+$$
+因此，扰动后的分布近似为：  
+$$
+f(x,y,t_1) \approx p \cdot g(x,y) + (1-p) \cdot h(x,y)
+$$
+这与初始平衡态的分布相同，说明网络在扰动后恢复了平衡态。
+
+
+
+### 系统稳定性分析
+
+**建立系统状态方程与平衡点**
+
+论文将随机移动网络的动态演化描述为一个一般的状态方程：
+
+$$
+\frac{dx}{dt} = f(x, t)
+$$
+其中，$x$ 是系统的 $n$ 维状态向量，$f(x, t)$ 是描述状态随时间变化的函数。
+
+- **平衡点定义**: 当存在一个状态 $x_e$ 满足对任意 $t$，有
+  $f(x_e, t) = 0$
+  这时 $x_e$ 就是系统的平衡状态。如论文中特别关注的网络平均度 $x_d$，不再随时间变化。
+
+**采用李雅普诺夫第二类方法**
+
+由于本系统状态向量各分量间关系复杂，且无法求出状态矩阵的全部特征值，所以不能采用第一类方法。因此选择构造“李雅普诺夫函数”（第二类方法）来验证系统的稳定性。
+
+**构造李雅普诺夫函数**
+$$
+V(x) = (x - x_e)^T P (x - x_e)
+$$
+其中 $P$ 是一个正定矩阵。由此保证：
+
+- **正定性**: 对于除 $x = x_e$ 外的所有状态，$V(x) > 0$；且在平衡点 $x_e$ 处有 $V(x_e) = 0$。
+
+**分析李雅普诺夫函数的时间导数**
+$$
+\dot{V}(x) = \frac{\partial V(x)}{\partial x} \cdot f(x, t)
+$$
+**平衡时 $\dot{V}(x) = 0$**: 当且仅当系统处于平衡状态 $x = x_e$ 时，有 $\dot{V}(x) = 0$。
+
+同时在平衡附近的非平衡状态下，由于选定的李雅普诺夫函数“能量”不会增加，从而得到$\dot{V}(x) ≤ 0$
--- a/科研/高飞论文.md
+++ b/科研/高飞论文.md
@ -165,3 +165,9 @@ LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$（其中 $d''$ 为 LSTM

 若整个网络有 $N$ 个节点，则最终预测结果的输出维度为 $N \times 2$（或 $N \times T' \times 2$，如果预测多个未来时刻）。

+
+
+### 疑问
+
+该论文可能有点问题，每个节点只能预测自身未来位置，无法获取全局位置信息。如果先LSTM后GCN可能可以！
+
--- a/自学/JavaWeb——后端.md
+++ b/自学/JavaWeb——后端.md
@ -405,6 +405,18 @@ public class DeptController {

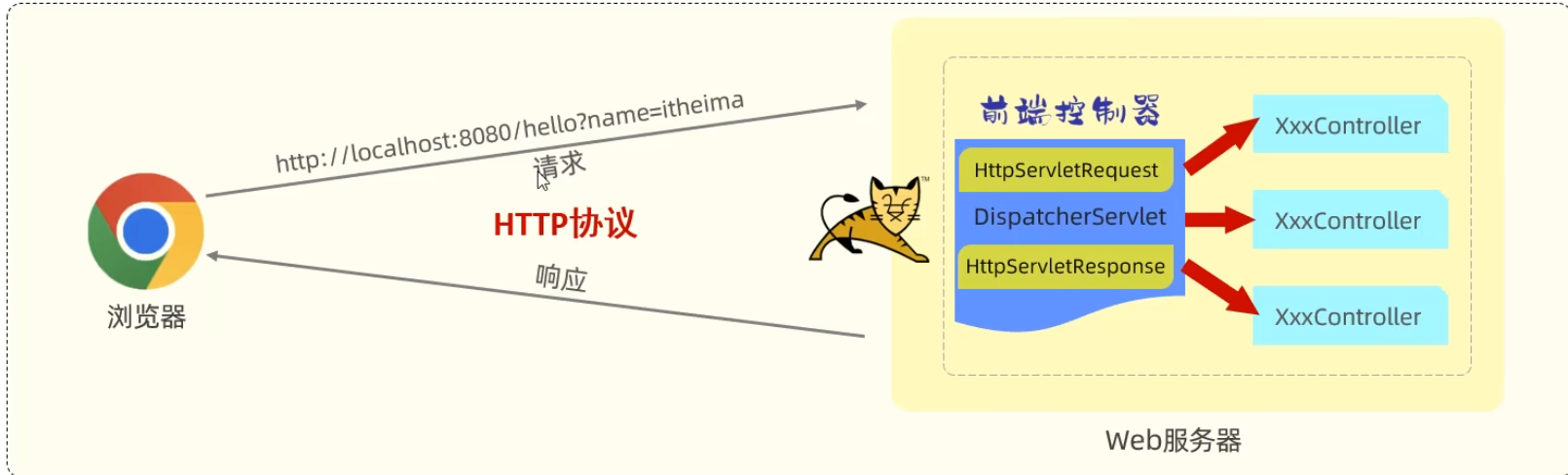
 ![image-20240304101816184](https://pic.bitday.top/i/2025/03/19/u6pju8-2.png)

+查看springboot版本：查看pom文件
+
+```java
+<parent>
+        <artifactId>spring-boot-starter-parent</artifactId>
+        <groupId>org.springframework.boot</groupId>
+        <version>2.7.3</version>
+</parent>
+```
+
+版本为2.7.3
+
 ### 快速启动

 1. 新建**spring initializr** project
@ -2265,6 +2277,21 @@ public class WebCorsConfig implements WebMvcConfigurer {

 ```

+
+
+**Nginx解决方案**
+
+统一域名入口：
+前端和 API 均通过 Nginx 以相同的域名（例如 https://example.com）提供服务。前端发送 AJAX 请求时，目标也是该域名的地址，如 https://example.com/api，从而避免了跨域校验。
+
+Nginx 作为中间代理：
+Nginx 将特定路径（例如 /api/）的请求转发到后端服务器。对浏览器来说，请求和响应均来自同一域名，代理过程对浏览器透明。
+
+“黑匣子”处理：
+浏览器只与 Nginx 交互，不关心 Nginx 内部如何转发请求。无论后端位置如何，浏览器都认为响应源自统一域名，从而解决跨域问题。
+
+
+
 **总结**

 普通的跨域请求依然会送达服务器，**服务器并不主动拦截**；它只是通过响应头声明哪些来源被允许访问，而真正的拦截与安全检查，则**由浏览器**根据同源策略来完成。
@ -2366,7 +2393,7 @@ String username = (String) claims.get("username");
 #### **JWT 登录认证流程**

 1. 用户登录
-   用户发起登录请求，登录成功后，生成 JWT 令牌，并将其返回给前端。
+   用户发起登录请求，校验密码、登录成功后，生成 JWT 令牌，并将其返回给前端。

 2. 前端存储令牌
   前端接收到 JWT 令牌，**存储在浏览器中**（通常存储在 LocalStorage 或 Cookie 中）。
@ -2393,7 +2420,7 @@ String username = (String) claims.get("username");
   后续的每次请求，前端将 JWT 令牌携带上。

 4. 服务端校验令牌
-   服务端接收到请求后，拦截请求并检查是否携带令牌。若没有令牌，拒绝访问；若令牌存在，校验令牌的**有效性**（包括有效期），若有效则放行，进行请求处理。
+   服务端接收到请求后，**拦截请求并检查是否携带令牌**。若没有令牌，拒绝访问；若令牌存在，校验令牌的**有效性**（包括有效期），若有效则放行，进行请求处理。



@ -2464,6 +2491,22 @@ public class WebConfig implements WebMvcConfigurer {
 }
 ```

+**WebMvcConfigurer接口**:
+
+**拦截器配置**
+通过实现 `addInterceptors` 方法，可以添加自定义的拦截器，从而在请求进入处理之前或之后执行一些逻辑操作，如权限校验、日志记录等。
+
+**静态资源映射**
+通过 `addResourceHandlers` 方法，可以自定义静态资源（如 HTML、CSS、JavaScript）的映射路径，这对于使用前后端分离或者集成第三方文档工具（如 Swagger/Knife4j）非常有用。
+
+**消息转换器扩展**
+通过 `extendMessageConverters` 方法，可以在默认配置的基础上，追加自定义的 HTTP 消息转换器，如将 Java 对象转换为 JSON 格式。
+
+**跨域配置**
+使用 `addCorsMappings` 方法，可以灵活配置跨域资源共享（CORS）策略，方便前后端跨域请求。
+
+
+
 #### 拦截路径

 `addPathPatterns`指定拦截路径；
--- a/自学/Java笔记本.md
+++ b/自学/Java笔记本.md
@ -164,6 +164,27 @@ public class SwitchCaseExample {



+6. 强制类型转换
+
+```java
+double sqrted=Math.sqrt(n);
+int soft_max=(int) sqrted;
+```
+
+
+
+7. Math库常用方法
+
+```java
+Math.pow(3, 2));     
+Math.sqrt(9));        
+Math.abs(a));        
+Math.max(a, b));   
+Math.min(a, b));   
+```
+
+
+
 #### Java传参方式

 基本数据类型（Primitives）
--- a/自学/力扣Hot
+++ b/自学/力扣Hot
@ -691,6 +691,8 @@ int[] partialArray = Arrays.copyOfRange(source, 1, 4);   //复制指定元素，

 初始化：

+int double 数值默认初始化为0，boolean默认初始化为false
+
 ```
 int[] memo = new int[nums.length];
 Arrays.fill(memo, -1);
@ -1983,3 +1985,43 @@ for (int j = 0; j <= capacity; j++) {
 - 内层循环正序，不要逆序！因为要利用已经更新的dp数组，允许同一物品重复使用！

 注意，完全背包和0/1背包的一维dp形式的递推公式一样，但是遍历顺序不同！！
+
+
+
+#### 多重背包
+
+有N种物品和一个容量为V 的背包。第i种物品**最多有Mi件可用**，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。
+
+|       | 重量 | 价值 | 数量 |
+| ----- | ---- | ---- | ---- |
+| 物品0 | 1    | 15   | 2    |
+| 物品1 | 3    | 20   | 3    |
+| 物品2 | 4    | 30   | 2    |
+
+把每种物品按数量展开，就**转化为0/1背包问题**了！相当于物品0-a 物品0-b  物品1-a ....，每个只能用一次。
+
+```java
+public int multipleKnapsack(int V, int[] weight, int[] value, int[] count) {
+    // 将每件物品按数量展开成 0/1 背包的多个物品
+    List<Integer> wList = new ArrayList<>();
+    List<Integer> vList = new ArrayList<>();
+    for (int i = 0; i < weight.length; i++) {
+        for (int k = 0; k < count[i]; k++) {
+            wList.add(weight[i]);
+            vList.add(value[i]);
+        }
+    }
+    // 0/1 背包 DP
+    int[] dp = new int[V + 1];
+    int N = wList.size();
+    for (int i = 0; i < N; i++) {
+        int wi = wList.get(i);
+        int vi = vList.get(i);
+        for (int j = V; j >= wi; j--) {
+            dp[j] = Math.max(dp[j], dp[j - wi] + vi);
+        }
+    }
+    return dp[V];
+}
+```
+
--- a/自学/苍穹外卖.md
+++ b/自学/苍穹外卖.md
@ -288,6 +288,10 @@ server{



+跨域问题：
+
+
+
 #### APIFox

 使用APIFox管理、测试接口、导出接口文档...
@ -331,7 +335,7 @@ APIFox 能够导入包括 YApi 格式在内的多种接口文档，同时支持

 **使用：**

-1. 导入 knife4j 的maven坐标
+**1.导入 knife4j 的maven坐标**

 在pom.xml中添加依赖

@ -342,7 +346,7 @@ APIFox 能够导入包括 YApi 格式在内的多种接口文档，同时支持
 </dependency>
 ```

-2. 在配置类中加入 knife4j 相关配置
+**2.在配置类中加入 knife4j 相关配置**

 WebMvcConfiguration.java

@ -368,7 +372,7 @@ WebMvcConfiguration.java
    }
 ```

-3. 设置静态资源映射，否则接口文档页面无法访问
+**3.设置静态资源映射，否则接口文档页面无法访问**

 WebMvcConfiguration.java

@ -383,6 +387,12 @@ protected void addResourceHandlers(ResourceHandlerRegistry registry) {
 }
 ```

+**4.访问测试**
+
+接口文档访问路径为 http://ip:port/doc.html ---> http://localhost:8080/doc.html
+
+这是根据后端 Java 代码（通常是注解）自动生成接口文档，访问是通过**后端服务的端口**，这些文档最终会以静态文件的形式存在于 jar 包内，通常存放在 `META-INF/resources/`
+


 **常用注解**
@ -414,62 +424,84 @@ public class EmployeeLoginDTO implements Serializable {

 ![image-20240327170247852](https://pic.bitday.top/i/2025/03/19/u7ybj9-2.png)

+EmployeeController.java
+
+```java
+@Api(tags = "员工相关接口")
+public class EmployeeController {
+
+    @Autowired
+    private EmployeeService employeeService;
+    @Autowired
+    private JwtProperties jwtProperties;
+    
+    /**
+     * 登录
+     *
+     * @param employeeLoginDTO
+     * @return
+     */
+    @PostMapping("/login")
+    @ApiOperation(value = "员工登录")
+    public Result<EmployeeLoginVO> login(@RequestBody EmployeeLoginDTO employeeLoginDTO) 		{
+        //..............     
+	}
+}
+
+```
+
+
+
 ## 开发

 ### 加密算法

-存放在数据表中的密码不能以明文存储，需对前端传来的密码进行加密。
+加密存储确保即使数据库泄露，攻击者也不能轻易获取用户原始密码。

 spring security中提供了一个加密类BCryptPasswordEncoder。

 它采用[哈希算法](https://so.csdn.net/so/search?q=哈希算法&spm=1001.2101.3001.7020) SHA-256 +随机盐+密钥对密码进行加密。加密算法是一种**可逆**的算法，而哈希算法是一种**不可逆**的算法。

-因为有随机盐的存在，所以相同的明文密码经过加密后的密码是**不一样**的，盐在加密的密码中是有记录的，所以需要对比的时候，springSecurity是可以从中获取到盐的
+因为有随机盐的存在，所以**相同的明文密码**经过加密后的密码是**不一样**的，盐在加密的密码中是有记录的，所以需要对比的时候，springSecurity是可以从中获取到盐的



- 添加依赖
+- 添加 spring-security-crypto 依赖,无需引入Spring Security 的认证、授权、过滤器链等其它安全组件！

-```java
+```xml
 <dependency>
-            <groupId>org.springframework.boot</groupId>
-            <artifactId>spring-boot-starter-security</artifactId>
-        </dependency>
+    <groupId>org.springframework.security</groupId>
+    <artifactId>spring-security-crypto</artifactId>
+</dependency>
 ```

 - 添加配置

 ```java
@Configuration
-@EnableWebSecurity
-public class WebSecurityConfig extends WebSecurityConfigurerAdapter {
-    @Override
-    protected void configure(HttpSecurity http) throws Exception {
-        http
-                .authorizeRequests()
-                .anyRequest().permitAll()  // 允许所有请求
-                .and()
-                .csrf().disable();  // 禁用CSRF保护
-    }
+public class SecurityConfig {
    @Bean
-    public BCryptPasswordEncoder encoder(){
-        return new BCryptPasswordEncoder();
+    public PasswordEncoder passwordEncoder() {
+        // 参数 strength 为工作因子，默认为 10，这里可以根据需要进行调整
+        return new BCryptPasswordEncoder(10);
    }
 }
 ```

- 使用
+- 用户注册、加密 **encode**

 ```java
@Autowired
-private BCryptPasswordEncoder bCryptPasswordEncoder;
+private PasswordEncoder passwordEncoder;
+// 对密码进行加密
+String encodedPassword = passwordEncoder.encode(rawPassword);
+```

-// 加密
-String encodedPassword=bCryptPasswordEncoder.encode(PasswordConstant.DEFAULT_PASSWORD);
-employee.setPassword(encodedPassword);
+- 验证密码  **matches**

-// 比较
-bCryptPasswordEncoder.matches(明文，密文);
+```java
+// 使用 matches 方法来对比明文密码和存储的哈希密码
+boolean judge= passwordEncoder.matches(rawPassword, user.getPassword());
 ```