Commit on 2025/04/13 周日 14:09:55.03
This commit is contained in:
parent
7dcaebcd75
commit
ef468a3e46
78
科研/循环神经网络.md
78
科研/循环神经网络.md
@ -169,7 +169,7 @@ GRU 通过两个门(gate)来控制信息的流动:
|
||||
这里:
|
||||
|
||||
- $r_t \odot h_{t-1}$ 表示**重置门** $r_t$ 和上一时刻隐藏状态的逐元素相乘(Hadamard 乘积),用以调制历史信息的影响;
|
||||
- $\tanh(\cdot)$ 用来生成候选隐藏状态,将输出限制在 $[-1, 1]$。
|
||||
- $\tanh(\cdot)$ 激活函数,用来生成候选隐藏状态,将输出限制在 $[-1, 1]$。
|
||||
|
||||
4. **最终隐藏状态 $h_t$**
|
||||
GRU 结合更新门和候选隐藏状态更新最终隐藏状态:
|
||||
@ -224,7 +224,7 @@ $$
|
||||
\begin{aligned}
|
||||
\textbf{遗忘门:} \quad f_t = \sigma\Big(W_{xf}\, x_t + W_{hf}\, h_{t-1} + b_f\Big) \\
|
||||
\textbf{输入门:} \quad i_t = \sigma\Big(W_{xi}\, x_t + W_{hi}\, h_{t-1} + b_i\Big) \\
|
||||
\textbf{输出门:} \quad o_t = \sigma\Big(W_{xo}\, x_t + W_{ho}\, h_{t-1} + b_o\Big) \\
|
||||
\textbf{输出门:} \quad o_t = \sigma\Big(W_{xo}\, x_t + W_{ho}\, h_{t-1} + b_o\Big) \\\\
|
||||
\textbf{候选细胞状态:} \quad \tilde{c}_t = \tanh\Big(W_{xc}\, x_t + W_{hc}\, h_{t-1} + b_c\Big) \\
|
||||
\textbf{细胞状态更新:} \quad c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \\
|
||||
\textbf{隐藏状态:} \quad h_t = o_t \odot \tanh(c_t)
|
||||
@ -235,13 +235,16 @@ $$
|
||||
### 直观理解
|
||||
|
||||
- **细胞状态 $c_t$**:
|
||||
细胞状态是贯穿整个序列的“记忆通道”,负责长期保存信息。它像一条传送带,在不同时间步中线性传递,避免信息被频繁修改,从而维持长期记忆。
|
||||
细胞状态是贯穿整个序列的“记忆通道”,负责长期保存信息。它像一条传送带,在不同时间步中线性传递,避免信息被频繁修改,**从而维持长期记忆**。
|
||||
- **遗忘门 $f_t$**:
|
||||
用于丢弃上一时刻不再需要的信息。如果遗忘门输出接近 0,说明遗忘了大部分过去的信息;如果接近 1,则保留大部分信息。
|
||||
**类比**:若模型遇到新段落,遗忘门可能关闭(输出接近0),丢弃前一段的无关信息;若需要延续上下文(如故事主线),则保持开启(输出接近1)。
|
||||
- **输入门 $i_t$ 和候选细胞状态 $\tilde{c}_t$**:
|
||||
输入门控制有多少候选信息被写入细胞状态。候选细胞状态是基于当前输入和上一时刻隐藏状态生成的新信息。
|
||||
**类比**:阅读时遇到关键情节,输入门打开,将新信息写入长期记忆(如角色关系),同时候选状态 $\tilde{c}_t$提供新信息的候选内容。
|
||||
|
||||
|
||||
|
||||
- **输出门 $o_t$**:
|
||||
控制从细胞状态中输出多少信息作为当前时间步的隐藏状态。隐藏状态 $h_t$ 通常用于后续计算(例如,生成输出、参与下一时刻计算)。
|
||||
**类比**:根据当前任务(如预测下一个词),输出门决定暴露细胞状态的哪部分(如只关注时间、地点等关键信息)。
|
||||
@ -252,39 +255,64 @@ $$
|
||||
|
||||
TCN是一种专为处理序列数据设计的深度学习架构。它通过结合因果卷积、扩张卷积和残差连接,解决了传统RNN和LSTM在并行化能力和梯度稳定性上的局限性。
|
||||
|
||||
**卷积操作**:与 RNN 逐步递归处理序列不同,TCN 利用一维卷积一次性对整个序列进行并行处理,这使得训练时可以充分利用硬件的并行计算能力。
|
||||
|
||||
### 1. 因果卷积(Causal Convolution)
|
||||
|
||||
因果卷积确保模型在预测时刻$t$的数据时,仅使用$t$时刻之前的信息,避免未来数据泄漏。
|
||||
|
||||
因果卷积类似于一个滑动窗口(窗口大小=$k$),每次用当前和过去的$k-1$个值加权求和,生成当前时刻的输出。
|
||||
因果卷积类似于一个滑动窗口(窗口大小=$k$),每次用当前和过去的$k-1$个值加权求和,生成当前时刻的输出。
|
||||
|
||||
通过以下调整保证因果性:
|
||||
|
||||
- **卷积核方向**:仅对当前及过去的时间步进行卷积。
|
||||
- **填充(Padding)**:在输入序列的**左侧填充 $(k-1)$ 个零**($k$ 为卷积核大小),确保输出长度与输入一致,且不泄露未来信息。
|
||||
|
||||
|
||||
|
||||
**公式定义**:
|
||||
|
||||
对于卷积核 $W \in \mathbb{R}^k$ 和输入 $X \in \mathbb{R}^T$,因果卷积的输出 $Y \in \mathbb{R}^T$ 为:
|
||||
$$
|
||||
F(x_{t}) = \sum_{i=0}^{k-1} f_{i} \cdot x_{t - i}
|
||||
Y_t = \sum_{i=0}^{k-1} W_i \cdot X_{t-i} \quad \text{(若 } t-i < 0 \text{,则 } X_{t-i}=0 \text{)}
|
||||
$$
|
||||
|
||||
- $x_t$:时刻$t$的输入数据
|
||||
- $f_i$:一维卷积核的第$i$个权重
|
||||
- $k$:卷积核大小
|
||||
|
||||
**举例:**
|
||||
|
||||
1. **输入序列**:$x = [x_0, x_1, x_2, x_3, x_4] = [1, 3, 2, 5, 4]$
|
||||
(长度为5的时间序列,$x_t$表示$t$时刻的值)
|
||||
2. **卷积核**:$f = [f_0, f_1] = [0.5, -1]$
|
||||
(大小为$k=2$,权重分别为$0.5$和$-1$)
|
||||
**示例**:
|
||||
|
||||
| 时刻 $t$ | 输入 $x_t$ | 计算过程 | 输出 $F(x_t)$ |
|
||||
| -------- | ---------- | ---------------------------- | -------------------- |
|
||||
| 0 | 1 | $0.5 \cdot 1 + (-1) \cdot 0$ | $0.5 \times 1 = 0.5$ |
|
||||
| 1 | 3 | $0.5 \cdot 3 + (-1) \cdot 1$ | $1.5 - 1 = 0.5$ |
|
||||
| 2 | 2 | $0.5 \cdot 2 + (-1) \cdot 3$ | $1 - 3 = -2$ |
|
||||
| 3 | 5 | $0.5 \cdot 5 + (-1) \cdot 2$ | $2.5 - 2 = 0.5$ |
|
||||
| 4 | 4 | $0.5 \cdot 4 + (-1) \cdot 5$ | $2 - 5 = -3$ |
|
||||
- 输入序列 $X$: `[x0, x1, x2, x3]`(长度 $T=4$)
|
||||
- 卷积核 $W$: `[w0, w1, w2]`(大小 $k=3$)
|
||||
- 输出 $Y$: `[y0, y1, y2, y3]`(与输入长度相同)
|
||||
|
||||
**输入填充**:左侧补 k−1=2*k*−1=2 个零,得到 `[0, 0, x0, x1, x2, x3]`
|
||||
|
||||
**通常卷积核需要翻转:**:`[w2, w1, w0]`
|
||||
|
||||
1. **计算 $y_0$($t=0$)**:
|
||||
$$
|
||||
y_0 = w0 \cdot x0 + w1 \cdot 0 + w2 \cdot 0 = w0 \cdot x0
|
||||
$$
|
||||
|
||||
2. **计算 $y_1$($t=1$)**:
|
||||
$$
|
||||
y_1 = w0 \cdot x1 + w1 \cdot x0 + w2 \cdot 0
|
||||
$$
|
||||
|
||||
3. **计算 $y_2$($t=2$)**:
|
||||
$$
|
||||
y_2 = w0 \cdot x2 + w1 \cdot x1 + w2 \cdot x0
|
||||
$$
|
||||
|
||||
4. **计算 $y_3$($t=3$)**:
|
||||
$$
|
||||
y_3 = w0 \cdot x3 + w1 \cdot x2 + w2 \cdot x1
|
||||
$$
|
||||
|
||||
### 最终输出
|
||||
|
||||
**最终输出序列**:
|
||||
$$
|
||||
F(x) = [0.5, 0.5, -2, 0.5, -3]
|
||||
Y = \left[ w0 x0, \; w0 x1 + w1 x0, \; w0 x2 + w1 x1 + w2 x0, \; w0 x3 + w1 x2 + w2 x1 \right]
|
||||
$$
|
||||
|
||||
|
||||
@ -293,12 +321,12 @@ $$
|
||||
|
||||
通过**膨胀因子 $d$**在卷积核元素之间插入空洞(间隔),从而在不增加参数量的情况下**扩大感受野**。
|
||||
|
||||
- **传统卷积**($d=1$):连续覆盖 $k$ 个时间步(如 $x_t, x_{t-1}, x_{t-2}$)。
|
||||
- **扩张卷积**($d>1$):跳跃式覆盖,跳过中间部分时间步(如 $x_t, x_{t-d}, x_{t-2d}$)。
|
||||
- **传统卷积**($d=1$):连续覆盖 $k$ 个时间步(如 $X_t, X_{t-1}, X_{t-2}$)。
|
||||
- **扩张卷积**($d>1$):跳跃式覆盖,跳过中间部分时间步(如 $X_t, X_{t-d}, X_{t-2d}$)。
|
||||
|
||||
**公式定义**:
|
||||
$$
|
||||
F(x_{t}) = \sum_{i=0}^{k-1} f_{i} \cdot x_{t - d \cdot i}
|
||||
Y_t = \sum_{i=0}^{k-1} W_i \cdot X_{t-d\cdot i} \quad
|
||||
$$
|
||||
|
||||
|
||||
|
||||
88
科研/草稿.md
88
科研/草稿.md
@ -1,43 +1,67 @@
|
||||
# 物理连通性约束说明
|
||||
这里涉及到的是神经网络中常用的全连接层(dense layer)的矩阵乘法约定,不同的表示方式会有不同的矩阵尺寸和乘法顺序,下面给出两种常见的约定,并解释如何让维度匹配:
|
||||
|
||||
## 约束目的
|
||||
**禁止在物理上不可能连通的位置新增链路**,确保网络拓扑优化的合理性。
|
||||
---
|
||||
|
||||
## 矩阵定义
|
||||
### 方法一:以行向量表示输入
|
||||
|
||||
1. **最大功率连通矩阵** $A_{\max}$:
|
||||
- 表示节点在最大发射功率下的连通性
|
||||
- 非零元素:$A_{\max,ij} \neq 0$ 表示可连通
|
||||
- 零元素:$A_{\max,ij} = 0$ 表示即使满功率也无法连通
|
||||
|
||||
2. **互补矩阵** $A'_{\max}$:
|
||||
1. **设定输入为行向量:**
|
||||
假设每个节点的隐藏状态由 LSTM 输出后表示为一个行向量,即
|
||||
$$
|
||||
A'_{\max,ij} =
|
||||
\begin{cases}
|
||||
0, & A_{\max,ij} \neq 0 \\
|
||||
1, & A_{\max,ij} = 0
|
||||
\end{cases}
|
||||
h_i \in \mathbb{R}^{1 \times d''}
|
||||
$$
|
||||
- 在物理不可连通位置为1,其他位置为0
|
||||
这里 $d''$ 是 LSTM 隐藏单元的数量。
|
||||
|
||||
## 约束条件
|
||||
$$
|
||||
A \odot A'_{\max} = 0
|
||||
$$
|
||||
2. **全连接层权重矩阵:**
|
||||
为了将行向量 $h_i$ 映射到预测的二维坐标,设计全连接层的权重矩阵 $W_{\text{fc}}$ 的尺寸为
|
||||
$$
|
||||
W_{\text{fc}} \in \mathbb{R}^{d'' \times 2}
|
||||
$$
|
||||
这样,乘法操作 $h_i \cdot W_{\text{fc}}$ 的计算是:
|
||||
- $h_i$ 的尺寸:$1 \times d''$
|
||||
- $W_{\text{fc}}$ 的尺寸:$d'' \times 2$
|
||||
- 相乘结果:$1 \times 2$
|
||||
|
||||
**解释**:
|
||||
- $\odot$ 表示Hadamard积(逐元素相乘)
|
||||
- 约束强制要求:对于所有满足 $A'_{\max,ij}=1$ 的位置(即物理不可连通的节点对),必须有 $A_{ij}=0$
|
||||
3. **加偏置得到最终输出:**
|
||||
同时,全连接层有一个偏置向量 $b_{\text{fc}} \in \mathbb{R}^{1 \times 2}$,故有
|
||||
$$
|
||||
\hat{y}_i = h_i \cdot W_{\text{fc}} + b_{\text{fc}} \in \mathbb{R}^{1 \times 2},
|
||||
$$
|
||||
表示该节点预测的二维坐标 $(x, y)$。
|
||||
|
||||
## 实际效果
|
||||
---
|
||||
|
||||
1. **可调连接**:
|
||||
- 原本能连通的节点对($A_{\max,ij} \neq 0$)可以根据优化目标自由调整
|
||||
### 方法二:以列向量表示输入
|
||||
|
||||
2. **固定断开**:
|
||||
- 物理上无法连通的节点对($A_{\max,ij} = 0$)始终保持断开($A_{ij} = 0$)
|
||||
1. **设定输入为列向量:**
|
||||
如果我们将每个节点的隐藏状态表示为列向量:
|
||||
$$
|
||||
h_i \in \mathbb{R}^{d'' \times 1},
|
||||
$$
|
||||
则需要调整矩阵乘法的顺序。
|
||||
|
||||
## 应用意义
|
||||
- 保证网络拓扑优化不违反物理层连接限制
|
||||
- 避免算法建议不切实际的通信链路
|
||||
- 维持网络部署的可行性
|
||||
2. **全连接层权重矩阵:**
|
||||
此时全连接层的权重矩阵应设置为
|
||||
$$
|
||||
W_{\text{fc}} \in \mathbb{R}^{2 \times d''},
|
||||
$$
|
||||
这样通过矩阵乘法:
|
||||
$$
|
||||
\hat{y}_i = W_{\text{fc}} \cdot h_i + b_{\text{fc}},
|
||||
$$
|
||||
- $W_{\text{fc}}$ 的尺寸:$2 \times d''$
|
||||
- $h_i$ 的尺寸:$d'' \times 1$
|
||||
- 乘积结果为:$2 \times 1$
|
||||
|
||||
对应的偏置 $b_{\text{fc}} \in \mathbb{R}^{2 \times 1}$ 后,最终输出为 $2 \times 1$(可以看作二维坐标)。
|
||||
|
||||
---
|
||||
|
||||
### 总结说明
|
||||
|
||||
- **两种约定等价:**
|
||||
实际实现时,只要保持输入和权重矩阵的乘法顺序一致,确保内维度匹配,输出最终都会是一个二维向量。在深度学习框架中(例如 Keras 或 PyTorch),通常默认每个样本以行向量形式表示(形状为 $(\text{batch\_size}, d'')$),因此全连接层权重设置为 $(d'', 2)$,计算 $h \cdot W$ 会得到形状为 $(\text{batch\_size}, 2)$ 的输出。
|
||||
|
||||
- **回答疑问:**
|
||||
“你这里 $W$ 和 $h$ 怎么能矩阵乘法呢”——关键在于你要统一向量的表示方式。如果你使用行向量表示每个节点,则 $h$ 的维度是 $1 \times d''$;对应的全连接层权重 $W_{\text{fc}}$ 为 $d'' \times 2$。这样乘法 $h \cdot W_{\text{fc}}$ 内维度 $d''$ 正好匹配,输出得到 $1 \times 2$ 的向量。如果反之使用列向量表示,则需要调整权重矩阵为 $2 \times d''$ 并将乘法表达为 $W_{\text{fc}} \cdot h$。
|
||||
|
||||
W_{\text{fc}} \in \mathbb{R}^{2 \times d''}
|
||||
|
||||
34
科研/颜佳佳论文.md
34
科研/颜佳佳论文.md
@ -256,7 +256,7 @@ PID控制接收机(AAGC/DAGC) → 实际Pr ≈ 目标Pr
|
||||
|
||||
|
||||
|
||||
## 智能体随机网络结构实时表示的应用
|
||||
## 基于谱聚类的无人机网络充电
|
||||
|
||||
### (1) 谱聚类分组Spectral_Clustering(表5.1)
|
||||
|
||||
@ -309,9 +309,41 @@ $$A_{ij} = \| \text{Position}_i - \text{Position}_j \|_2$$
|
||||
|
||||
|
||||
|
||||
## 基于T-GAT的无人机群流量预测
|
||||
|
||||
### TCN
|
||||
|
||||
流量矩阵 $X \in \mathbb{R}^{N \times T}$,其中:
|
||||
|
||||
- $N$:无人机节点数量(例如10架无人机)。
|
||||
- $T$:时间步数量。
|
||||
- 每个元素 $X_{i,t}$ 表示第 $i$ 个节点在时间 $t$ 的**总流量**(如发送/接收的数据包数量或带宽占用)。
|
||||
|
||||
**流量矩阵的形状**
|
||||
|
||||
假设有3架无人机,记录5个时间步的流量数据,矩阵如下:
|
||||
$$
|
||||
X = \begin{bmatrix} 100 & 150 & 200 & 180 & 220 \\[6pt] 50 & 75 & 100 & 90 & 110 \\[6pt] 80 & 120 & 160 & 140 & 170 \end{bmatrix}
|
||||
$$
|
||||
|
||||
|
||||
- **行 ($N=3$)**:每行代表一架无人机的历史流量序列(例如第1行表示无人机1的流量变化:100 → 150 → 200 → 180 → 220)。
|
||||
- **列 ($T=5$)**:每列代表所有无人机在**同一时间步**的流量状态(例如第1列表示在时间 $t_1$ 时,三架无人机的流量分别为:[100, 50, 80])。
|
||||
|
||||
**TCN处理流量矩阵**:
|
||||
|
||||
- **卷积操作**
|
||||
TCN 的每个卷积核会滑动扫描所有**通道**(即所有无人机)的时序数据。
|
||||
**例如**,一个大小为 3 的卷积核会同时分析每架无人机连续 3 个时间步的流量(例如从 $t_1$ 到 $t_3$),以提取局部时序模式。
|
||||
- **输出时序特征**
|
||||
经过多层扩张卷积和残差连接后,TCN 会输出一个高阶特征矩阵 $H_T^l$,其形状与输入类似(例如 `(1, 3, 5)`),但每个时间步的值已包含了:
|
||||
- **趋势信息**:流量上升或下降的长期规律。
|
||||
|
||||
TCN的卷积核仅在**单个通道内滑动**,计算时仅依赖该节点自身的历史时间步。节点间的交互是通过后续的**图注意力网络(GAT)**实现的。
|
||||
|
||||
### 与 GAT 的衔接
|
||||
|
||||
- TCN 输出的特征矩阵 $H_T^l$ 会传递给 GAT 进行进一步处理。
|
||||
- **时间步对齐**:通常取最后一个时间步的特征(例如 `H_T^l[:, :, -1]`)作为当前节点特征。
|
||||
- **空间聚合**:GAT 根据邻接矩阵计算无人机间的注意力权重,例如考虑“无人机2的当前流量可能受到无人机1过去3分钟流量变化的影响”。
|
||||
|
||||
|
||||
167
科研/高飞论文.md
Normal file
167
科研/高飞论文.md
Normal file
@ -0,0 +1,167 @@
|
||||
# 高飞论文
|
||||
|
||||
## 网络重构分析
|
||||
|
||||
假设网络中有 $n$ 个节点,则矩阵 $A(G)$ 的维度为 $n \times n$,预测得到特征值和特征向量后,可以根据矩阵谱分解理论进行逆向重构网络邻接矩阵,表示如下:
|
||||
|
||||
$$
|
||||
A(G) = \sum_{i=1}^n \hat{\lambda}_i \hat{x}_i \hat{x}_i^T
|
||||
$$
|
||||
|
||||
其中 $\hat{\lambda}_i$ 和 $\hat{x}_i$ 分别为通过预测得到矩阵 $A(G)$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差,直接进行矩阵重构会使得重构误差较大。 对于这个问题,文献提出一种 0/1 矩阵近似恢复算法。
|
||||
$$
|
||||
a_{ij} =
|
||||
\begin{cases}
|
||||
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
|
||||
0, & \text{else}
|
||||
\end{cases}
|
||||
$$
|
||||
只要我们的估计值与真实值之间差距**小于 0.5**,就能保证阈值处理以后准确地恢复原边信息。
|
||||
|
||||
|
||||
|
||||
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
|
||||
|
||||
真实矩阵 $A(G)$ 与预测矩阵 $\hat{A}(G) $ 之间的差为
|
||||
$$
|
||||
A(G) - \hat{A}(G) = \sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
|
||||
$$
|
||||
对于任意元素 $(i, j)$ 上有
|
||||
$$
|
||||
\left| \sum_{m=1}^n \Delta \lambda_m (\hat{x}_m \hat{x}_m^T)_{ij} \right| = |a_{ij} - \hat{a}_{ij}| < \frac{1}{2}
|
||||
$$
|
||||
|
||||
于一个归一化的特征向量 $\hat{x}_m$,其外积矩阵 $\hat{x}_m \hat{x}_m^T$ 的元素理论上满足
|
||||
$$
|
||||
|(\hat{x}_m \hat{x}_m^T)_{ij}| \leq 1.
|
||||
$$
|
||||
经过分析推导可以得出发生特征扰动时,网络精准重构条件为:
|
||||
$$
|
||||
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
|
||||
$$
|
||||
|
||||
$$
|
||||
\Delta {\lambda} < \frac{1}{2n}
|
||||
$$
|
||||
|
||||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
||||
|
||||
|
||||
|
||||
如果在**高层次**(特征值滤波)的误差累积超过了一定阈值,就有可能在**低层次**(邻接矩阵元素)中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5,就可以保证0-1矩阵的精确重构。
|
||||
|
||||
|
||||
|
||||
## 基于时空特征的节点位置预测
|
||||
|
||||
在本模型中,整个预测流程分为两大模块:
|
||||
|
||||
- **GCN 模块:主要用于从当前网络拓扑中提取每个节点的**空间表示**。这里的输入主要包括:
|
||||
- **邻接矩阵 $A$**:反映网络中节点之间的连通关系,维度为 $N \times N$,其中 $N$ 表示节点数。(可通过第二章网络重构的方式获取)
|
||||
- **特征矩阵 $H^{(0)}$**:一般是原始节点的属性信息,如历史位置数据,其维度为 $N \times d$,其中 $d$ 是初始特征维度。
|
||||
|
||||
- **LSTM 模块**:用于捕捉节点随时间变化的动态信息,对每个节点的历史运动轨迹进行序列建模,并预测未来时刻的坐标。
|
||||
其输入通常是经过 GCN 模块处理后,每个节点在一段时间内获得的时空融合特征序列,维度一般为 $N \times T \times d'$,其中 $T$ 表示时间步数,$d'$ 是经过 GCN 后的特征维度。
|
||||
|
||||
|
||||
|
||||
### GCN 模块
|
||||
|
||||
#### 输入
|
||||
|
||||
- **邻接矩阵 $A$**:维度 $N \times N$。在实际操作中,通常先加上自环形成
|
||||
$$
|
||||
\hat{A} = A + I.
|
||||
$$
|
||||
|
||||
- **特征矩阵 $H^{(0)}$**:维度 $N \times d$,每一行对应一个节点的初始特征(例如历史采样的位置信息或其他描述)。
|
||||
|
||||
#### 图卷积操作
|
||||
|
||||
常用的图卷积计算公式为:
|
||||
$$
|
||||
H^{(l+1)} = \sigma \Bigl(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} H^{(l)} W^{(l)} \Bigr)
|
||||
$$
|
||||
其中:
|
||||
|
||||
- $\tilde{A} = A + I$ 为加上自环后的邻接矩阵,
|
||||
- $\tilde{D}$ 为 $\tilde{A}$ 的度矩阵,定义为 $\tilde{D}_{ii} = \sum_{j}\tilde{A}_{ij}$;
|
||||
- $H^{(l)}$ 表示第 $l$ 层的节点特征,初始时 $H^{(0)}$ 就是输入特征矩阵;
|
||||
- $W^{(l)}$ 是第 $l$ 层的权重矩阵,其维度通常为 $d_l \times d_{l+1}$(例如从 $d$ 到 $d'$);
|
||||
- $\sigma(\cdot)$ 是非线性激活函数,例如 ReLU 或 tanh。
|
||||
|
||||
经过一层或多层图卷积后,可以得到最终的节点表示矩阵 $H^{(L)}$(或记为 $X$),维度为 $N \times d'$。
|
||||
其中:
|
||||
|
||||
- 每一行 $x_i \in \mathbb{R}^{d'}$ 表示节点 $i$ 的空间特征,这些特征综合反映了其在网络拓扑中的位置及与邻居的关系。
|
||||
|
||||
#### 输出
|
||||
|
||||
- **GCN 输出**:形状为 $N \times d'$;若将模型用于时序建模,则对于每个时间步,都可以得到这样一个节点特征表示。
|
||||
- 这里 $d'>d$ 。1.高维嵌入不仅保留了绝对位置信息,还包括了网络拓扑信息。2.兼容下游LSTM任务需求。
|
||||
|
||||
|
||||
|
||||
### LSTM 模块
|
||||
|
||||
#### 输入数据构造
|
||||
|
||||
在时序预测中,对于每个节点,我们通常有一段历史数据序列。假设我们采集了最近 $T$ 个时刻的数据,然后采用“滑动窗口”的方式,预测 $T+1$、 $T+2$...
|
||||
|
||||
- 对于每个时刻 $t$,节点 $i$ 的空间特征 $x_i^{(t)} \in \mathbb{R}^{d'}$ 由 GCN 得到;
|
||||
|
||||
- 将这些特征按照时间顺序排列,得到一个序列:
|
||||
$$
|
||||
X_i = \bigl[ x_i^{(t-T+1)},\, x_i^{(t-T+2)},\, \dots,\, x_i^{(t)} \bigr] \quad \in \mathbb{R}^{T \times d'}.
|
||||
$$
|
||||
|
||||
对于整个网络来说,可以将数据看作一个三维张量,维度为 $(N, T, d')$。
|
||||
|
||||
#### LSTM 内部运作
|
||||
|
||||
LSTM 通过内部门控机制(遗忘门 $f_t$、输入门 $i_t$ 和输出门 $o_t$)来更新其记忆状态 $C_t$ 和隐藏状态 $h_t$。公式如下
|
||||
|
||||
- **遗忘门**:
|
||||
$$
|
||||
f_t = \sigma(W_f [h_{t-1},\, x_t] + b_f)
|
||||
$$
|
||||
|
||||
- **输入门和候选记忆**:
|
||||
$$
|
||||
i_t = \sigma(W_i [h_{t-1},\, x_t] + b_i) \quad,\quad \tilde{C}_t = \tanh(W_C [h_{t-1},\, x_t] + b_C)
|
||||
$$
|
||||
|
||||
- **记忆更新**:
|
||||
$$
|
||||
C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t
|
||||
$$
|
||||
|
||||
- **输出门和隐藏状态**:
|
||||
$$
|
||||
o_t = \sigma(W_o [h_{t-1},\, x_t] + b_o), \quad h_t = o_t \odot \tanh(C_t)
|
||||
$$
|
||||
|
||||
|
||||
|
||||
其中,$x_t$ 在这里对应每个节点在时刻 $t$ 的 GCN 输出特征;
|
||||
$[h_{t-1},\, x_t]$ 为连接后的向量;
|
||||
|
||||
LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$(其中 $d''$ 为 LSTM 的隐藏单元数)捕捉了时间上的依赖信息。
|
||||
|
||||
#### 输出与预测
|
||||
|
||||
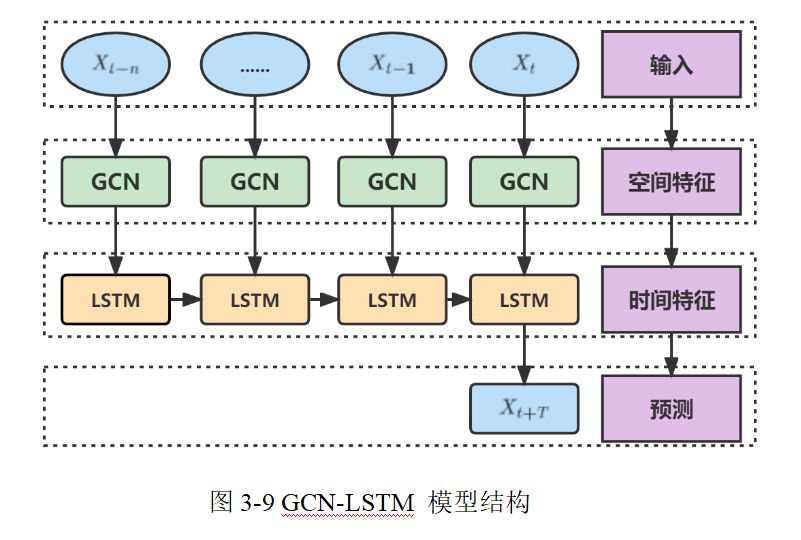
最后,经过 LSTM 处理后,我们在最后一个时间步获得最终的隐藏状态 $h_t$ 或使用整个序列的输出;接着通过一个全连接层(FC层)将隐藏状态映射到最终的预测输出。
|
||||
|
||||
- **全连接层转换公式**:
|
||||
$$
|
||||
\hat{y}_i = W_{\text{fc}} \cdot h_t + b_{\text{fc}}
|
||||
$$
|
||||
|
||||
其中,假设预测的是二维坐标(例如 $x$ 和 $y$ 坐标),$W_{\text{fc}} \in \mathbb{R}^{2 \times d''}$,输出 $\hat{y}_i \in \mathbb{R}^2$ 表示节点 $i$ 在未来某个时刻(或下一时刻)的预测坐标。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
若整个网络有 $N$ 个节点,则最终预测结果的输出维度为 $N \times 2$(或 $N \times T' \times 2$,如果预测多个未来时刻)。
|
||||
|
||||
545
自学/力扣Hot 100题.md
545
自学/力扣Hot 100题.md
@ -1,13 +1,13 @@
|
||||
## 力扣Hot 100题
|
||||
# 力扣Hot 100题
|
||||
|
||||
### 杂项
|
||||
## 杂项
|
||||
|
||||
- **最大值**:`Integer.MAX_VALUE`
|
||||
- **最小值**:`Integer.MIN_VALUE`
|
||||
|
||||
|
||||
|
||||
#### **数组集合比较**
|
||||
### **数组集合比较**
|
||||
|
||||
**`Arrays.equals(array1, array2)`**
|
||||
|
||||
@ -50,7 +50,7 @@ if (flag == false) { //更常用!
|
||||
|
||||
|
||||
|
||||
#### Character好用的方法
|
||||
### Character好用的方法
|
||||
|
||||
`Character.isDigit(char c)`用于判断一个字符是否是一个数字字符
|
||||
|
||||
@ -62,13 +62,13 @@ if (flag == false) { //更常用!
|
||||
|
||||
|
||||
|
||||
#### Integer好用的方法
|
||||
### Integer好用的方法
|
||||
|
||||
`Integer.parseInt(String s)`:将字符串 `s` 解析为一个整数(`int`)。
|
||||
|
||||
`Integer.toString(int i)`:将 `int` 转换为字符串。
|
||||
|
||||
`Integer.compare(int a,int b)` 比较a和b的大小,内部实现:
|
||||
`Integer.compare(int a,int b)` 比较a和b的大小,内部实现类似:
|
||||
|
||||
```
|
||||
public static int compare(int x, int y) {
|
||||
@ -76,13 +76,13 @@ public static int compare(int x, int y) {
|
||||
}
|
||||
```
|
||||
|
||||
避免了 **整数溢出** 的风险,在排序中建议使用`Integer.compare(int a,int b)`代替 `a-b`
|
||||
避免了 **整数溢出** 的风险,在排序中建议使用`Integer.compare(a,b)`代替 `a-b`。注意,仅支持Integer[] arr,不支持int[] arr。
|
||||
|
||||
|
||||
|
||||
### 常用数据结构
|
||||
## 常用数据结构
|
||||
|
||||
#### String
|
||||
### String
|
||||
|
||||
子串:字符串中**连续的一段字符**。
|
||||
|
||||
@ -117,7 +117,7 @@ String sortedStr = new String(charArray);
|
||||
|
||||
|
||||
|
||||
#### StringBuffer
|
||||
### StringBuffer
|
||||
|
||||
`StringBuffer` 是 Java 中用于操作可变字符串的类
|
||||
|
||||
@ -172,7 +172,7 @@ sb.setLength(0);
|
||||
|
||||
|
||||
|
||||
#### HashMap
|
||||
### HashMap
|
||||
|
||||
- 基于哈希表实现,查找、插入和删除的平均时间复杂度为 O(1)。
|
||||
- 不保证元素的顺序。
|
||||
@ -230,7 +230,7 @@ visited[i][j] = true;
|
||||
|
||||
|
||||
|
||||
#### HashSet
|
||||
### HashSet
|
||||
|
||||
- 基于哈希表实现,查找、插入和删除的平均时间复杂度为 O(1)。
|
||||
|
||||
@ -273,7 +273,7 @@ visited[i][j] = true;
|
||||
|
||||
|
||||
|
||||
#### PriorityQueue
|
||||
### PriorityQueue
|
||||
|
||||
- 基于优先堆(最小堆或最大堆)实现,元素按优先级排序。
|
||||
- **默认是最小堆**,即队首元素是最小的。 `new PriorityQueue<>(Comparator.reverseOrder());`定义最大堆
|
||||
@ -400,7 +400,7 @@ PriorityQueue<int[]> minHeap = new PriorityQueue<>(new Comparator<int[]>() {
|
||||
|
||||
|
||||
|
||||
##### **自己实现小根堆:**
|
||||
#### **自己实现小根堆:**
|
||||
|
||||
**父节点**:对于任意索引 `i`,其父节点的索引为 `(i - 1) // 2`。
|
||||
|
||||
@ -511,7 +511,7 @@ class MinHeap {
|
||||
|
||||
|
||||
|
||||
#### **ArrayList**
|
||||
### **ArrayList**
|
||||
|
||||
- 基于数组实现,支持动态扩展。
|
||||
- 访问元素的时间复杂度为 O(1),在末尾插入和删除的时间复杂度为 O(1)。
|
||||
@ -607,7 +607,7 @@ for (int i = 0; i < list.size(); i++) {
|
||||
|
||||
|
||||
|
||||
#### **数组(Array)**
|
||||
### **数组(Array)**
|
||||
|
||||
数组是一种固定长度的数据结构,用于存储相同类型的元素。数组的特点包括:
|
||||
|
||||
@ -698,7 +698,7 @@ Arrays.fill(memo, -1);
|
||||
|
||||
|
||||
|
||||
#### 二维数组
|
||||
### 二维数组
|
||||
|
||||
```java
|
||||
int rows = 3;
|
||||
@ -731,10 +731,12 @@ public void setZeroes(int[][] matrix) {
|
||||
}
|
||||
```
|
||||
|
||||
[[1, 0]] 是一行两列数组。
|
||||
|
||||
|
||||
|
||||
#### Queue
|
||||
|
||||
### Queue
|
||||
|
||||
队尾插入,队头取!
|
||||
|
||||
@ -771,7 +773,8 @@ public class QueueExample {
|
||||
```
|
||||
|
||||
|
||||
#### Deque(双端队列+栈)
|
||||
|
||||
### Deque(双端队列+栈)
|
||||
|
||||
支持在队列的两端(头和尾)进行元素的插入和删除。这使得 Deque 既能作为队列(FIFO)又能作为栈(LIFO)使用。
|
||||
|
||||
@ -857,7 +860,7 @@ public class DequeExample {
|
||||
|
||||
|
||||
|
||||
#### Iterator
|
||||
### Iterator
|
||||
|
||||
- **`HashMap`、`HashSet`、`ArrayList` 和 `PriorityQueue`** 都实现了 `Iterable` 接口,支持 `iterator()` 方法。
|
||||
|
||||
@ -893,7 +896,7 @@ public class Main {
|
||||
|
||||
|
||||
|
||||
### 排序
|
||||
## 排序
|
||||
|
||||
排序时间复杂度:O(nlog(n))
|
||||
|
||||
@ -901,7 +904,7 @@ public class Main {
|
||||
|
||||
|
||||
|
||||
#### 快速排序
|
||||
### 快速排序
|
||||
|
||||
**基本思想:**
|
||||
|
||||
@ -964,7 +967,7 @@ public class QuickSortWithSwap {
|
||||
|
||||
|
||||
|
||||
#### 冒泡排序
|
||||
### 冒泡排序
|
||||
|
||||
**基本思想:**
|
||||
|
||||
@ -1005,7 +1008,7 @@ public void bubbleSort(int[] arr){
|
||||
|
||||
|
||||
|
||||
#### 归并排序
|
||||
### 归并排序
|
||||
|
||||
**基本思想:**
|
||||
|
||||
@ -1076,7 +1079,9 @@ public class MergeSort {
|
||||
|
||||
|
||||
|
||||
#### **数组排序**
|
||||
### 数组排序
|
||||
|
||||
默认升序:
|
||||
|
||||
```java
|
||||
import java.util.Arrays;
|
||||
@ -1092,7 +1097,55 @@ public class ArraySortExample {
|
||||
|
||||
|
||||
|
||||
#### 集合排序
|
||||
自定义降序:
|
||||
|
||||
注意:如果数组元素是对象(例如 `Integer`、`String` 或自定义类)那么可以利用 `Arrays.sort()` 方法配合自定义的比较器(Comparator)实现降序排序。例如,对于 `Integer` 数组,可以这样写:
|
||||
|
||||
```java
|
||||
public class DescendingSortExample {
|
||||
public static void main(String[] args) {
|
||||
// 创建一个Integer数组
|
||||
Integer[] arr = {5, 2, 9, 1, 5, 6};
|
||||
|
||||
// 使用Comparator进行降序排序(使用lambda表达式)
|
||||
Arrays.sort(arr, (a, b) -> b - a);
|
||||
// 或者使用Collections.reverseOrder()也可以:
|
||||
// Arrays.sort(arr, Collections.reverseOrder());
|
||||
|
||||
// 输出排序后的数组
|
||||
System.out.println(Arrays.toString(arr));
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
对于基本数据类型的数组(如 `int[]`、`double[]` 等),`Arrays.sort()` 方法**仅支持升序排序**,需要先对数组进行升序排序,然后反转数组元素顺序!。
|
||||
|
||||
```java
|
||||
public class DescendingPrimitiveSort {
|
||||
public static void main(String[] args) {
|
||||
int[] arr = {5, 2, 9, 1, 5, 6};
|
||||
|
||||
// 先排序(升序)
|
||||
Arrays.sort(arr);
|
||||
|
||||
// 反转数组
|
||||
for (int i = 0; i < arr.length / 2; i++) {
|
||||
int temp = arr[i];
|
||||
arr[i] = arr[arr.length - 1 - i];
|
||||
arr[arr.length - 1 - i] = temp;
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
System.out.println(Arrays.toString(arr));
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 集合排序
|
||||
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
@ -1121,7 +1174,7 @@ public class ListSortExample {
|
||||
|
||||
|
||||
|
||||
#### **自定义排序**
|
||||
### 自定义排序
|
||||
|
||||
要实现接口自定义排序,必须实现 `Comparator<T>` 接口的 `compare(T o1, T o2)` 方法。
|
||||
|
||||
@ -1211,7 +1264,7 @@ public class ComparatorSortExample {
|
||||
|
||||
|
||||
|
||||
### 题型
|
||||
## 题型
|
||||
|
||||
常见术语:
|
||||
|
||||
@ -1230,7 +1283,7 @@ public class ComparatorSortExample {
|
||||
|
||||
|
||||
|
||||
#### 哈希
|
||||
### 哈希
|
||||
|
||||
**问题分析**:
|
||||
|
||||
@ -1246,7 +1299,7 @@ public class ComparatorSortExample {
|
||||
3. **去重**:
|
||||
- 需要去除重复元素时,`HashSet` 可以有效实现。
|
||||
|
||||
#### 双指针
|
||||
### 双指针
|
||||
|
||||
题型:
|
||||
|
||||
@ -1278,7 +1331,7 @@ public class ComparatorSortExample {
|
||||
|
||||
|
||||
|
||||
#### 前缀和
|
||||
### 前缀和
|
||||
|
||||
1. **前缀和的定义**
|
||||
定义前缀和 `preSum[i]` 为数组 `nums` 从索引 0 到 i 的元素和,即
|
||||
@ -1312,7 +1365,7 @@ public class ComparatorSortExample {
|
||||
|
||||
|
||||
|
||||
#### **遍历二叉树**
|
||||
### **遍历二叉树**
|
||||
|
||||
*递归法中序*
|
||||
|
||||
@ -1410,7 +1463,7 @@ public List<List<Integer>> levelOrder(TreeNode root) {
|
||||
|
||||
|
||||
|
||||
#### 回溯法
|
||||
### 回溯法
|
||||
|
||||
回溯算法用于 **搜索一个问题的所有的解** ,即爆搜(暴力解法),通过深度优先遍历的思想实现。核心思想是:
|
||||
|
||||
@ -1472,7 +1525,7 @@ public class Permute {
|
||||
|
||||
|
||||
|
||||
#### 大小根堆
|
||||
### 大小根堆
|
||||
|
||||
**题目描述**:给定一个整数数组 `nums` 和一个整数 `k`,返回出现频率最高的前 `k` 个元素,返回顺序可以任意。
|
||||
|
||||
@ -1506,3 +1559,427 @@ public class Permute {
|
||||
| ------ | --------------- | ---------- | ---------- |
|
||||
| 大根堆 | k ≈ n,简单易写 | O(n log n) | O(n) |
|
||||
| 小根堆 | k ≪ n,更高效 | O(n log k) | O(n) |
|
||||
|
||||
|
||||
|
||||
### 动态规划
|
||||
|
||||
解题步骤:
|
||||
|
||||
**确定 dp 数组以及下标的含义(很关键!不跑偏)**
|
||||
|
||||
- 目的:明确 dp 数组中存储的状态或结果。
|
||||
- 关键:下标往往对应问题中的一个“阶段”或“子问题”,而数组的值则表示这一阶段的最优解或累计结果。
|
||||
- 示例:在背包问题中,可以设 `dp[i]` 表示前 `i` 个物品能够达到的最大价值。
|
||||
|
||||
**确定递推公式**
|
||||
|
||||
- 目的:找到状态之间的转移关系,表明如何从已解决的子问题求解更大规模的问题。
|
||||
|
||||
- 关键:分析每个状态可能来源于哪些小状态,写出数学或逻辑表达式。
|
||||
|
||||
- 示例:对于 0-1 背包问题,递推公式通常为
|
||||
$$
|
||||
dp[i]=max(dp[i],dp[i−weight]+value)
|
||||
$$
|
||||
|
||||
**dp 数组如何初始化**
|
||||
|
||||
- 目的:给定初始状态,为所有可能情况设置基础值。
|
||||
- 关键:通常初始化基础的情况(如 `dp[0]=0`),或者用极大或极小值标示未计算状态。
|
||||
- 示例:在求最短路径问题中,可以用较大值(如 `infinity`)初始化所有状态,然后设定起点状态为 0。
|
||||
|
||||
**确定遍历顺序**
|
||||
|
||||
- 目的:按照正确的顺序计算每个状态,确保依赖的子问题都已经计算完毕。
|
||||
- 关键:遍历顺序需要与递推公式保持一致,既可以是正向(从小到大)也可以是反向(从大到小),取决于问题要求。
|
||||
- 示例:对背包问题,为避免重复计算,每个物品的更新通常采用反向遍历。
|
||||
|
||||
**举例推导 dp 数组**
|
||||
|
||||
- 目的:通过一个具体例子来演示递推公式的应用,直观理解每一步计算。
|
||||
- 关键:选择简单案例,从初始化、更新到最终结果展示整个过程。
|
||||
- 示例:对一个简单的路径问题,展示如何从起点逐步更新 dp 数组,最后得到终点的最优解。
|
||||
|
||||
|
||||
|
||||
**例题**
|
||||
|
||||
* 题目: 746. 使用最小花费爬楼梯 (MinCostClimbingStairs)
|
||||
* 描述:给你一个整数数组 cost ,其中 cost[i] 是从楼梯**第 i 个台阶向上爬需要支付的费用**。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
|
||||
* 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
|
||||
* 请你计算并返回达到楼梯顶部的最低花费。
|
||||
|
||||
示例 2:
|
||||
输入:cost = [10,15,20]
|
||||
输出:15
|
||||
解释:你将从下标为 1 的台阶开始。
|
||||
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
|
||||
总花费为 15 。
|
||||
|
||||
* 链接:https://leetcode.cn/problems/min-cost-climbing-stairs/
|
||||
|
||||
|
||||
|
||||
1.确定dp数组以及下标的含义
|
||||
|
||||
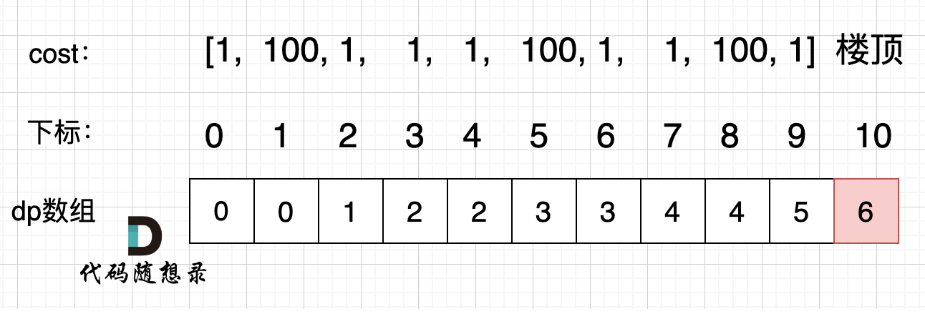
**dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]**。
|
||||
|
||||
2.确定递推公式
|
||||
|
||||
**可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]**。
|
||||
|
||||
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
|
||||
|
||||
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
|
||||
|
||||
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
|
||||
|
||||
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
|
||||
|
||||
3.dp数组如何初始化
|
||||
|
||||
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]、dp[1]推出。
|
||||
|
||||
由“你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” =》初始化 dp[0] = 0,dp[1] = 0
|
||||
|
||||
4.确定遍历顺序
|
||||
|
||||
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
|
||||
|
||||
5.举例推导dp数组
|
||||
|
||||
拿示例:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 背包问题
|
||||
|
||||
总结:背包问题不仅可以求**能装的物品的最大价值**,还可以求**背包是否可以装满**,还可以求**组合总和**。
|
||||
|
||||
|
||||
|
||||
**背包是否可以装满示例说明**
|
||||
|
||||
假设背包容量为 10,物品的重量分别为 [3, 4, 7]。我们希望判断是否可以恰好填满容量 10。
|
||||
|
||||
其中 dp[j] 表示在容量 j 下,能装入的**最大重量**(保证不超过 j)。如果dp[10]=10,代表能装满
|
||||
|
||||
```java
|
||||
public boolean canFillBackpack(int[] weights, int capacity) {
|
||||
// dp[j] 表示在不超过背包容量 j 的前提下,能装入的最大重量
|
||||
int[] dp = new int[capacity + 1];
|
||||
// 初始状态: 背包容量为0时,能够装入的重量为0,其他位置初始为0
|
||||
|
||||
// 遍历每一个物品(0/1背包,每个物品只能使用一次)
|
||||
for (int i = 0; i < weights.length; i++) {
|
||||
// 逆序遍历背包容量,防止当前物品被重复使用
|
||||
for (int j = capacity; j >= weights[i]; j--) {
|
||||
dp[j] = Math.max(dp[j], dp[j - weights[i]] + weights[i]);
|
||||
}
|
||||
}
|
||||
|
||||
// 如果 dp[capacity] 恰好等于 capacity,则说明背包正好被装满
|
||||
return dp[capacity] == capacity;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**求组合总和**
|
||||
|
||||
统计数组中有多少种组合(子集)使得其和正好为 P ?
|
||||
|
||||
dp[j] 表示从数组中选取若干个数,使得这些数的和正好为 j 的方法数。
|
||||
|
||||
状态转移:
|
||||
对于数组中的每个数字 numnumnum,从 dp 数组后向前(逆序)遍历,更新:
|
||||
|
||||
dp[j]=dp[j]+dp[j−num]
|
||||
|
||||
这里的意思是:
|
||||
|
||||
- 如果不选当前数字,方法数保持不变;
|
||||
- 如果选当前数字,那么原来凑出和 j−num 的方案都可以扩展成凑出和 j 的方案。
|
||||
|
||||
初始条件:
|
||||
|
||||
- dp[0] = 1,代表凑出和为 0 只有一种方式,即不选任何数字。
|
||||
|
||||
|
||||
|
||||
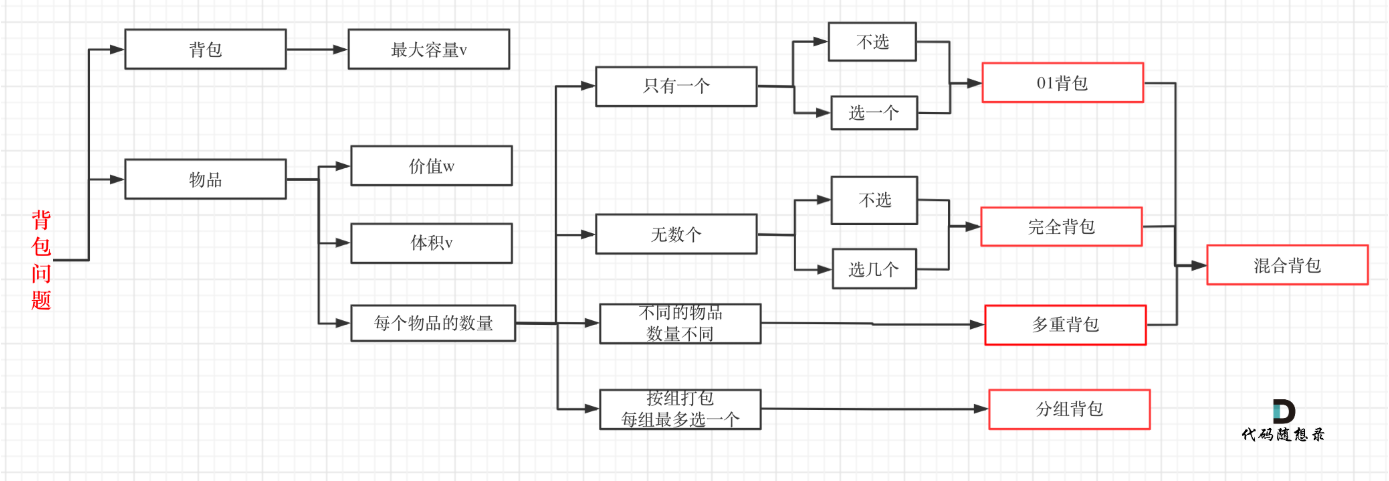
[代码随想录](https://programmercarl.com/背包理论基础01背包-1.html#算法公开课)
|
||||
|
||||
|
||||
|
||||
完全背包是01背包稍作变化而来,即:完全背包的物品数量是无限的。
|
||||
|
||||
#### 0/1背包(一)
|
||||
|
||||
描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品只能用一次**,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/11/r292zm-0.png" alt="image-20250411163635562" style="zoom: 80%;" />
|
||||
|
||||
**1.确定dp数组以及下标的含义**
|
||||
|
||||
因为有两个维度需要分别表示:物品 和 背包容量,所以 dp为二维数组。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/11/r0xkd9-0.png" alt="image-20250411163414119" style="zoom: 67%;" />
|
||||
|
||||
即 **dp\[i\]\[j\] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少**。
|
||||
|
||||
**2. 确定递推公式**
|
||||
|
||||
考虑dp\[i][j],有两种情况:
|
||||
|
||||
- **不放物品i**:背包容量为j,里面不放物品i的最大价值是 dp\[i - 1][j]。
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为 j - weight[i],dp\[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp\[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
递归公式: `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
|
||||
|
||||
**3. dp数组如何初始化**
|
||||
|
||||
(1)首先从dp\[i][j]的定义出发,如果背包容量j为0的话,即dp\[i][0],无论是选取哪些物品,背包价值总和一定为0。
|
||||
|
||||
(2)由状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
|
||||
此时就看存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
(3)其他地方初始化为0
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/11/r9skxy-0.png" alt="image-20250411164902801" style="zoom:67%;" />
|
||||
|
||||
**4.确定遍历顺序**
|
||||
|
||||
都可以,但推荐**先遍历物品**
|
||||
|
||||
```cpp
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**5.举例推导dp数组**
|
||||
|
||||
略
|
||||
|
||||
**代码:**
|
||||
|
||||
```
|
||||
public int knapsack(int[] weight, int[] value, int capacity) {
|
||||
int n = weight.length; // 物品的总个数
|
||||
|
||||
// 定义二维 dp 数组:
|
||||
// dp[i][j] 表示从下标为 [0, i] 的物品中任意选择,放入容量为 j 的背包中,能够获得的最大价值
|
||||
int[][] dp = new int[n][capacity + 1];
|
||||
|
||||
// 1. 初始化第 0 行:只考虑第 0 个物品的情况
|
||||
// 当背包容量 j >= weight[0] 时,可以选择放入第 0 个物品,价值为 value[0];否则为 0
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
if (j >= weight[0]) {
|
||||
dp[0][j] = value[0];
|
||||
} else {
|
||||
dp[0][j] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
// 2. 状态转移:从第 1 个物品开始,逐步填表
|
||||
// 遍历物品,物品下标从 1 到 n-1
|
||||
for (int i = 1; i < n; i++) {
|
||||
// 遍历背包容量,从 0 到 capacity
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 情况一:不放第 i 个物品,则最大价值不变,继承上一行的值
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
|
||||
// 情况二:如果当前背包容量 j 大于等于物品 i 的重量,则考虑放入当前物品
|
||||
if (j >= weight[i]) {
|
||||
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 返回考虑所有物品,背包容量为 capacity 时的最大价值
|
||||
return dp[n - 1][capacity];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 0/1背包(二)
|
||||
|
||||
**可以将二维 dp 优化为一维 dp 的典型条件包括:**
|
||||
|
||||
1.状态转移只依赖于之前的状态(例如上一行或上一个层次),而不是当前行中动态更新的状态。
|
||||
|
||||
- 例如在 0/1 背包问题中,二维 dp\[i][j] 只依赖于 dp\[i-1][j] 和 dp\[i-1][j - weight[i]]。
|
||||
|
||||
2.存在确定的遍历顺序(例如逆序或正序)能够确保在更新一维 dp 时,所依赖的值不会被当前更新覆盖。
|
||||
|
||||
- **逆序遍历**:例如 0/1 背包问题,为了防止同一个物品被重复使用,需要对容量 j 从大到小遍历,确保 dp[j - weight] 的值还是上一轮(上一行)的。
|
||||
|
||||
- **正序遍历**:在一些问题中,如果状态更新不会导致当前状态被重复利用(例如完全背包问题),可以顺序遍历。
|
||||
|
||||
3.状态数足够简单,不需要记录多维信息,仅一个维度的状态即可准确表示和转移问题状态。
|
||||
|
||||
|
||||
|
||||
**1.确定 dp 数组以及下标的含义**
|
||||
|
||||
使用一维 dp 数组 `dp[j]` 表示「在当前考虑的物品下,背包容量为 j 时能够获得的最大价值」。
|
||||
|
||||
**2.确定递推公式**
|
||||
当考虑当前物品 i(重量为 weight[i],价值为 value[i])时,有两种选择:
|
||||
|
||||
- **不选当前物品 i:**
|
||||
此时的最大价值为 dp[j](即前面的状态没有变化)。
|
||||
- **选当前物品 i:**
|
||||
当背包容量至少为 weight[i] 时,如果选择物品 i,剩余容量变为 j - weight[i],则最大价值为 dp[j - weight[i]] 加上 value[i]。
|
||||
|
||||
因此,状态转移方程为:
|
||||
$$
|
||||
dp[j]=max(dp[j], dp[j−weight[i]]+value[i])
|
||||
$$
|
||||
**3.dp 数组如何初始化**
|
||||
|
||||
`dp[0] = 0`,表示当背包容量为 0 时,能获得的最大价值自然为 0。
|
||||
|
||||
对于其他容量 dp[j],初始值也设为 0,dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。确保值不被初始值覆盖即可。
|
||||
|
||||
**4.一维dp数组遍历顺序**
|
||||
|
||||
外层遍历物品: 从第一个物品到最后一个物品,依次做决策。
|
||||
|
||||
内层遍历背包容量(**逆序遍历**): 遍历容量从 capacity 到当前物品的重量,进行状态更新。
|
||||
|
||||
- 逆序遍历的目的在于确保当前物品在更新过程中只会被使用一次,因为 dp[j - weight[i]] 代表的是上一轮(当前物品未使用前)的状态,不会被当前物品更新后的状态覆盖。
|
||||
|
||||
|
||||
|
||||
假设物品 $w=2$, $v=3$,背包容量 $C=5$。
|
||||
|
||||
错误的正序遍历($j=2 \to 5$)
|
||||
|
||||
1. $j=2$:
|
||||
$dp[2] = \max(0, dp[0]+3) = 3$
|
||||
$\Rightarrow dp = [0, 0, 3, 0, 0, 0]$
|
||||
2. $j=4$:
|
||||
$dp[4] = \max(0, dp[2]+3) = 6$
|
||||
$\Rightarrow$ **错误**:物品被重复使用两次!
|
||||
|
||||
**5.举例推导dp数组**
|
||||
|
||||
略
|
||||
|
||||
**代码:**
|
||||
|
||||
```java
|
||||
public int knapsack(int[] weight, int[] value, int capacity) {
|
||||
int n = weight.length;
|
||||
// 定义 dp 数组,dp[j] 表示背包容量为 j 时的最大价值
|
||||
int[] dp = new int[capacity + 1];
|
||||
|
||||
// 初始化:所有 dp[j] 初始为0,dp[0] = 0(无须显式赋值)
|
||||
|
||||
// 外层:遍历每一个物品
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 内层:逆序遍历背包容量,保证每个物品只被选择一次
|
||||
for (int j = capacity; j >= weight[i]; j--) {
|
||||
// 更新状态:选择不放入或者放入当前物品后的最大价值
|
||||
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
|
||||
// 返回背包总容量为 capacity 时获得的最大价值
|
||||
return dp[capacity];
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 完全背包(一)
|
||||
|
||||
**完全背包和01背包问题唯一不同的地方就是,每种物品有无限件**。
|
||||
|
||||
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品都有无限个(也就是可以放入背包多次)**,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
例:背包最大重量为4,物品为:
|
||||
|
||||
| 物品 | 重量 | 价值 |
|
||||
| ----- | ---- | ---- |
|
||||
| 物品0 | 1 | 15 |
|
||||
| 物品1 | 3 | 20 |
|
||||
| 物品2 | 4 | 30 |
|
||||
|
||||
**1. 确定dp数组以及下标的含义**
|
||||
|
||||
dp\[i][j] 表示从下标为[0-i]的物品,每个物品可以取无限次,放进容量为j的背包,价值总和最大是多少。
|
||||
|
||||
**2. 确定递推公式**
|
||||
|
||||
- **不放物品i**:背包容量为j,里面不放物品i的最大价值是dp\[i - 1][j]。
|
||||
- **放物品i**:背包空出物品i的容量后,背包容量为j - weight[i],dp\[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp\[i][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
递推公式: `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);`
|
||||
|
||||
01背包中是 `dp[i - 1][j - weight[i]] + value[i])`
|
||||
|
||||
因为在完全背包中,物品是可以放无限个,所以 即使空出物品1空间重量,那背包中也可能还有物品1,所以此时我们依然考虑放 物品0 和 物品1 的最大价值即: **dp\[1][1], 而不是 dp\[0][1]**。而0/1背包中,**既然空出物品1,那背包中也不会再有物品1**,即dp\[0][1]。
|
||||
|
||||
```java
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 不选物品 i,价值不变
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
// 如果当前背包容量 j 能放下物品 i,则考虑选取物品 i(完全背包内层循环正序或逆序都可以,但这里通常建议正序)
|
||||
if (j >= weight[i]) {
|
||||
// 注意:这里选取物品 i 后仍然可以继续选取物品 i,
|
||||
// 所以状态转移方程为 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
|
||||
dp[i][j] = Math.max(dp[i][j], dp[i][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**3. dp数组如何初始化**
|
||||
|
||||
- 如果背包容量j为0的话,即dp\[i][0],无论是选取哪些物品,背包价值总和一定为0。
|
||||
- 由递推公式,有一个方向 i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。即:存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
```java
|
||||
for (int j = 0; j <= capacity; j++) {
|
||||
// 当 j 小于第 0 个物品重量时,无法选取,所以价值为 0
|
||||
if (j < weight[0]) {
|
||||
dp[0][j] = 0;
|
||||
} else {
|
||||
// 完全背包允许多次使用物品 0,所以递归地累加
|
||||
dp[0][j] = dp[0][j - weight[0]] + value[0];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**4. 确定遍历顺序**
|
||||
|
||||
先物品或先背包容量都可,但推荐先物品。
|
||||
|
||||
|
||||
|
||||
#### 完全背包(二)
|
||||
|
||||
压缩成一维dp数组,也就是将上一层拷贝到当前层。
|
||||
|
||||
将上一层dp[i-1] 的那一层拷贝到 当前层 dp[i] ,那么递推公式由 `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])` 变成: `dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])`
|
||||
|
||||
压缩成一维,即`dp[j] = max(dp[j], dp[j - weight[i]] + value[i])`
|
||||
|
||||
- 根据题型选择先遍历物品或者背包,**如果求组合数就是外层for循环遍历物品,内层for遍历背包**。**如果求排列数就是外层for遍历背包,内层for循环遍历物品**。
|
||||
**组合不强调元素之间的顺序,排列强调元素之间的顺序**。
|
||||
- 内层循环正序,不要逆序!因为要利用已经更新的dp数组,允许同一物品重复使用!
|
||||
|
||||
注意,完全背包和0/1背包的一维dp形式的递推公式一样,但是遍历顺序不同!!
|
||||
|
||||
274
自学/苍穹外卖.md
274
自学/苍穹外卖.md
@ -1,10 +1,165 @@
|
||||
# 苍穹外卖
|
||||
|
||||
## 开发环境搭建
|
||||
## 项目简介
|
||||
|
||||
### 后端项目结构
|
||||
### 整体介绍
|
||||
|
||||
|
||||
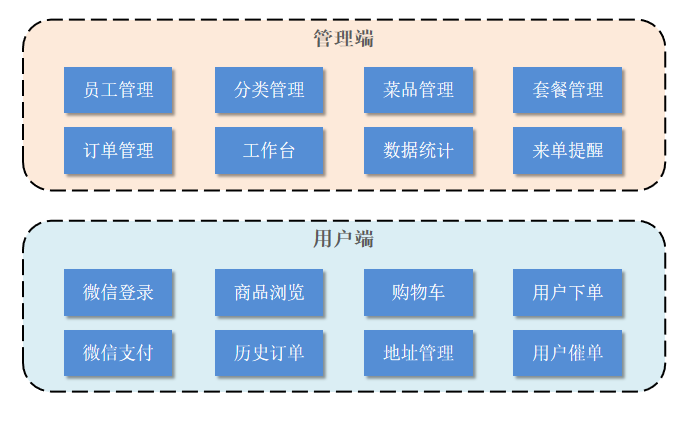
本项目(苍穹外卖)是专门为餐饮企业(餐厅、饭店)定制的一款软件产品,包括 **系统管理后台** 和 **小程序端应用** 两部分。其中系统管理后台主要提供给餐饮企业内部员工使用,可以对餐厅的分类、菜品、套餐、订单、员工等进行管理维护,对餐厅的各类数据进行统计,同时也可进行来单语音播报功能。小程序端主要提供给消费者使用,可以在线浏览菜品、添加购物车、下单、支付、催单等。
|
||||
|
||||
|
||||
|
||||
**1). 管理端功能**
|
||||
|
||||
员工登录/退出 , 员工信息管理 , 分类管理 , 菜品管理 , 套餐管理 , 菜品口味管理 , 订单管理 ,数据统计,来单提醒。
|
||||
|
||||
**2). 用户端功能**
|
||||
|
||||
微信登录 , 收件人地址管理 , 用户历史订单查询 , 菜品规格查询 , 购物车功能 , 下单 , 支付、分类及菜品浏览。
|
||||
|
||||
|
||||
|
||||
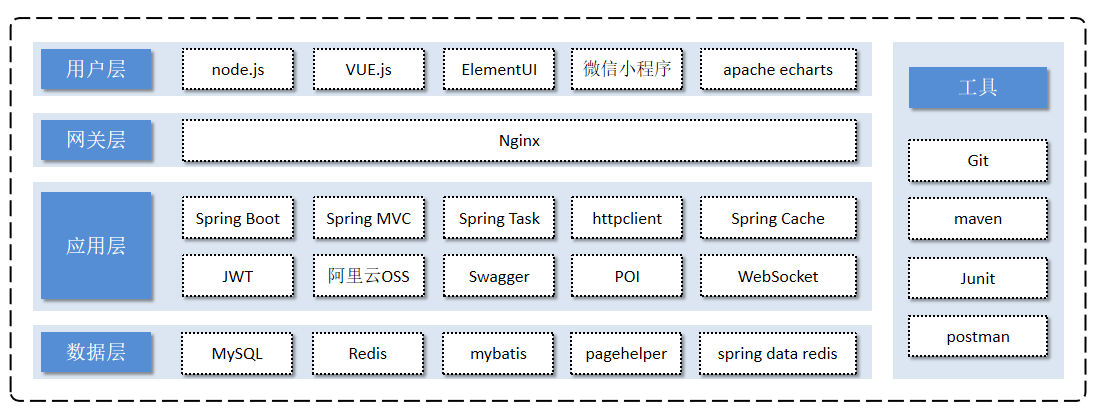
### 技术选型
|
||||
|
||||
|
||||
|
||||
**1). 用户层**
|
||||
|
||||
本项目中在构建系统管理后台的前端页面,我们会用到H5、Vue.js、ElementUI、apache echarts(展示图表)等技术。而在构建移动端应用时,我们会使用到微信小程序。
|
||||
|
||||
|
||||
|
||||
**2). 网关层**
|
||||
|
||||
Nginx是一个服务器,主要用来作为Http服务器,部署静态资源,访问性能高。在Nginx中还有两个比较重要的作用: 反向代理和负载均衡, 在进行项目部署时,要实现Tomcat的负载均衡,就可以通过Nginx来实现。
|
||||
|
||||
|
||||
|
||||
**3). 应用层**
|
||||
|
||||
SpringBoot: 快速构建Spring项目, 采用 "约定优于配置" 的思想, 简化Spring项目的配置开发。
|
||||
|
||||
SpringMVC:SpringMVC是spring框架的一个模块,springmvc和spring无需通过中间整合层进行整合,可以无缝集成。
|
||||
|
||||
Spring Task: 由Spring提供的定时任务框架。
|
||||
|
||||
httpclient: 主要实现了对http请求的发送。
|
||||
|
||||
Spring Cache: 由Spring提供的数据缓存框架
|
||||
|
||||
JWT: 用于对应用程序上的用户进行身份验证的标记。
|
||||
|
||||
阿里云OSS: 对象存储服务,在项目中主要存储文件,如图片等。
|
||||
|
||||
Swagger: 可以自动的帮助开发人员生成接口文档,并对接口进行测试。
|
||||
|
||||
POI: 封装了对Excel表格的常用操作。
|
||||
|
||||
WebSocket: 一种通信网络协议,使客户端和服务器之间的数据交换更加简单,用于项目的来单、催单功能实现。
|
||||
|
||||
|
||||
|
||||
**4). 数据层**
|
||||
|
||||
MySQL: 关系型数据库, 本项目的核心业务数据都会采用MySQL进行存储。
|
||||
|
||||
Redis: 基于key-value格式存储的内存数据库, 访问速度快, 经常使用它做缓存。
|
||||
|
||||
Mybatis: 本项目持久层将会使用Mybatis开发。
|
||||
|
||||
pagehelper: 分页插件。
|
||||
|
||||
spring data redis: 简化java代码操作Redis的API。
|
||||
|
||||
|
||||
|
||||
**5). 工具**
|
||||
|
||||
git: 版本控制工具, 在团队协作中, 使用该工具对项目中的代码进行管理。
|
||||
|
||||
maven: 项目构建工具。
|
||||
|
||||
junit:单元测试工具,开发人员功能实现完毕后,需要通过junit对功能进行单元测试。
|
||||
|
||||
postman: 接口测工具,模拟用户发起的各类HTTP请求,获取对应的响应结果。
|
||||
|
||||
|
||||
|
||||
### 准备工作
|
||||
|
||||
//待完善,最后写一套本地java开发、nginx部署前端;服务器docker部署的方案!!!
|
||||
|
||||
#### 前端环境搭建
|
||||
|
||||
1.构建和打包前端项目
|
||||
|
||||
```bash
|
||||
npm run build
|
||||
```
|
||||
|
||||
2.将构建文件复制到指定目录
|
||||
|
||||
Nginx 默认的静态文件根目录通常是 **`/usr/share/nginx/html`**,你可以选择将打包好的静态文件拷贝到该目录
|
||||
|
||||
或者使用自定义目录`/var/www/my-frontend`,并修改 Nginx 配置文件来指向这个目录。
|
||||
|
||||
3.配置 Nginx
|
||||
|
||||
打开 Nginx 的配置文件,通常位于 `/etc/nginx/nginx.conf`
|
||||
|
||||
以下是一个使用自定义目录 `/var/www/my-frontend` 作为站点根目录的示例配置:
|
||||
|
||||
```nginx
|
||||
server {
|
||||
listen 80;
|
||||
server_name your-domain.com; # 如果没有域名可以使用 _ 或 localhost
|
||||
|
||||
root /var/www/my-frontend;
|
||||
index index.html;
|
||||
|
||||
location / {
|
||||
try_files $uri $uri/ /index.html;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
4.启动或重启 Nginx
|
||||
|
||||
```bash
|
||||
sudo nginx -t # 检查配置是否正确
|
||||
sudo systemctl restart nginx # 重启 Nginx 服务
|
||||
```
|
||||
|
||||
5.访问前端项目
|
||||
|
||||
在浏览器中输入你配置的域名或服务器 IP 地址
|
||||
|
||||
|
||||
|
||||
#### 后端环境搭建
|
||||
|
||||
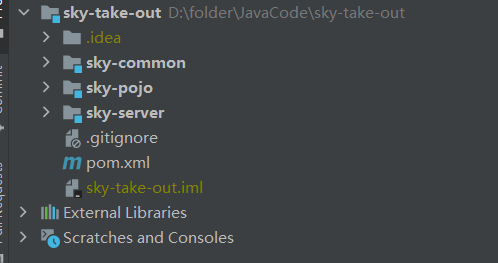
|
||||
|
||||
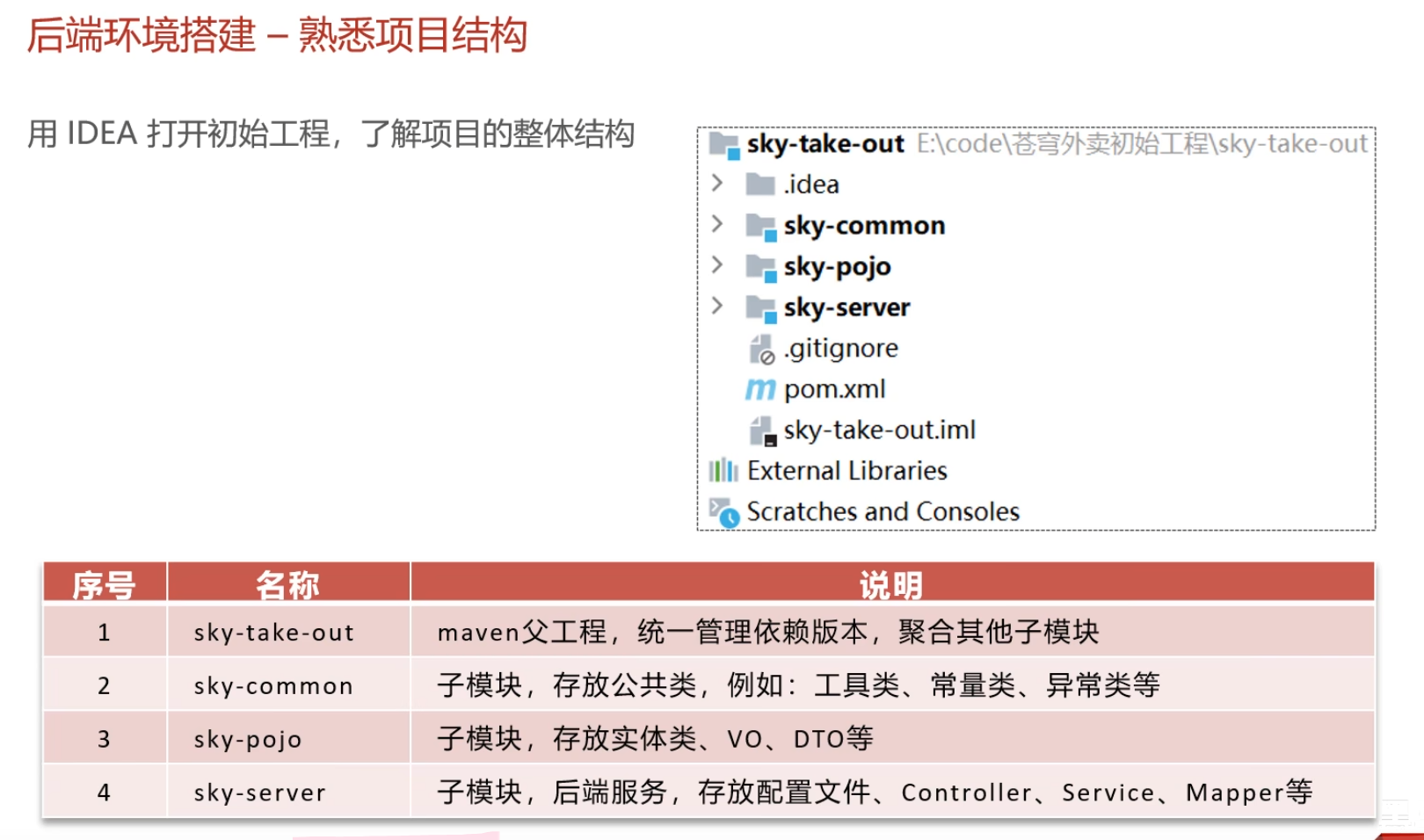
工程的每个模块作用说明:
|
||||
|
||||
| **序号** | **名称** | **说明** |
|
||||
| -------- | ------------ | ------------------------------------------------------------ |
|
||||
| 1 | sky-take-out | maven父工程,统一管理依赖版本,聚合其他子模块 |
|
||||
| 2 | sky-common | 子模块,存放公共类,例如:工具类、常量类、异常类等 |
|
||||
| 3 | sky-pojo | 子模块,存放实体类、VO、DTO等 |
|
||||
| 4 | sky-server | 子模块,后端服务,存放配置文件、Controller、Service、Mapper等 |
|
||||
|
||||
分析sky-common模块的每个包的作用:
|
||||
|
||||
| 名称 | 说明 |
|
||||
| ----------- | ------------------------------ |
|
||||
| constant | 存放相关常量类 |
|
||||
| context | 存放上下文类 |
|
||||
| enumeration | 项目的枚举类存储 |
|
||||
| exception | 存放自定义异常类 |
|
||||
| json | 处理json转换的类 |
|
||||
| properties | 存放SpringBoot相关的配置属性类 |
|
||||
| result | 返回结果类的封装 |
|
||||
| utils | 常用工具类 |
|
||||
|
||||
分析sky-pojo模块的每个包的作用:
|
||||
|
||||
@ -15,7 +170,22 @@
|
||||
| VO | 视图对象,为前端展示数据提供的对象(响应给web) |
|
||||
| POJO | 普通Java对象,只有属性和对应的getter和setter |
|
||||
|
||||
### 数据库设计文档
|
||||
分析sky-server模块的每个包的作用:
|
||||
|
||||
| 名称 | 说明 |
|
||||
| -------------- | ---------------- |
|
||||
| config | 存放配置类 |
|
||||
| controller | 存放controller类 |
|
||||
| interceptor | 存放拦截器类 |
|
||||
| mapper | 存放mapper接口 |
|
||||
| service | 存放service类 |
|
||||
| SkyApplication | 启动类 |
|
||||
|
||||
|
||||
|
||||
#### 数据库初始化
|
||||
|
||||
执行sky.sql文件
|
||||
|
||||
| 序号 | 数据表名 | 中文名称 |
|
||||
| ---- | ------------- | -------------- |
|
||||
@ -33,41 +203,46 @@
|
||||
|
||||
|
||||
|
||||
```java
|
||||
@TableName("user")
|
||||
public class User {
|
||||
@TableId
|
||||
private Long id;
|
||||
#### Nginx
|
||||
|
||||
private String name;
|
||||
**1.静态资源托管**
|
||||
|
||||
private Integer age;
|
||||
直接高效地托管前端静态文件(HTML/CSS/JS/图片等)。
|
||||
|
||||
@TableField("isMarried")
|
||||
private Boolean isMarried;
|
||||
|
||||
@TableField("`order`")
|
||||
private String order;
|
||||
```nginx
|
||||
server {
|
||||
root /var/www/html;
|
||||
index index.html;
|
||||
location / {
|
||||
try_files $uri $uri/ /index.html; # 支持前端路由(如 React/Vue)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
- **`try_files`**:按顺序尝试多个文件或路径,直到找到第一个可用的为止。
|
||||
- `$uri`:尝试直接访问请求的路径对应的文件(例如 `/css/style.css`)。
|
||||
- `$uri/`:尝试将路径视为目录(例如 `/blog/` 会查找 `/blog/index.html`)。
|
||||
- `/index.html`:如果前两者均未找到,最终返回前端入口文件 `index.html`。
|
||||
|
||||
|
||||
**1.nginx 反向代理的好处:**
|
||||
|
||||
**2.nginx 反向代理:**
|
||||
|
||||
**反向代理的好处:**
|
||||
|
||||
- 提高访问速度
|
||||
|
||||
因为nginx本身可以进行缓存,如果访问的同一接口,并且做了数据缓存,nginx就直接可把数据返回,不需要真正地访问服务端,从而提高访问速度。
|
||||
|
||||
- 进行负载均衡
|
||||
|
||||
所谓负载均衡,就是把大量的请求按照我们指定的方式均衡的分配给集群中的每台服务器。
|
||||
|
||||
- 保证后端服务安全
|
||||
|
||||
因为一般后台服务地址不会暴露,所以使用浏览器不能直接访问,可以把nginx作为请求访问的入口,请求到达nginx后转发到具体的服务中,从而保证后端服务的安全。
|
||||
|
||||
- 统一入口解决跨域问题(无需后端配置 CORS)。
|
||||
|
||||
```java
|
||||
**nginx 反向代理的配置方式:**
|
||||
|
||||
```nginx
|
||||
server{
|
||||
listen 80;
|
||||
server_name localhost;
|
||||
@ -78,11 +253,15 @@ server{
|
||||
}
|
||||
```
|
||||
|
||||
当在访问http://localhost/api/employee/login,nginx接收到请求后转到http://localhost:8080/admin/,故最终的请求地址为http://localhost:8080/admin/employee/login
|
||||
监听80端口号, 然后当我们访问 http://localhost:80/api/../..这样的接口的时候,它会通过 location /api/ {} 这样的反向代理到 http://localhost:8080/admin/上来。
|
||||
|
||||
**2.负载均衡配置**(有两个后端服务器)
|
||||
|
||||
```java
|
||||
|
||||
**3.负载均衡配置**(默认是轮询)
|
||||
|
||||
将流量分发到多个后端服务器,提升系统吞吐量和容错能力。
|
||||
|
||||
```nginx
|
||||
upstream webservers{
|
||||
server 192.168.100.128:8080;
|
||||
server 192.168.100.129:8080;
|
||||
@ -99,7 +278,50 @@ server{
|
||||
|
||||
|
||||
|
||||
### Swagger
|
||||
**完整流程示例**
|
||||
|
||||
1. **用户访问**:浏览器打开 `http://yourdomain.com`。
|
||||
2. **Nginx 返回静态文件**:返回 `index.html` 和前端资源。
|
||||
3. **前端发起 API 请求**:前端代码调用 `/api/data`。
|
||||
4. **Nginx 代理请求**:将 `/api/data` 转发到 `http://backend_server:3000/api/data`。
|
||||
5. **后端响应**:处理请求并返回数据,Nginx 将结果传回前端。
|
||||
|
||||
|
||||
|
||||
#### APIFox
|
||||
|
||||
使用APIFox管理、测试接口、导出接口文档...
|
||||
|
||||
**优势:**
|
||||
|
||||
1.多格式支持
|
||||
APIFox 能够导入包括 YApi 格式在内的多种接口文档,同时支持导出为 OpenAPI、Postman Collection、Markdown 和 HTML 等格式,使得接口文档在不同工具间无缝迁移和使用。
|
||||
|
||||
2.接口调试与 Mock
|
||||
内置接口调试工具可以直接发送请求、查看返回结果,同时内置 Mock 服务功能,方便前后端联调和接口数据模拟,提升开发效率。
|
||||
|
||||
3.易用性与团队协作
|
||||
界面直观、操作便捷,支持多人协作,通过分支管理和版本控制,团队成员可以并行开发并进行变更管理,确保接口维护有序。
|
||||
|
||||
|
||||
|
||||
**迭代分支功能:**
|
||||
|
||||
新建迭代分支,新增的待测试的接口在这里充分测试,没问题之后合并回主分支。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/10/tvvptv-0.png" alt="image-20250410180705866" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
**导出接口文档:**
|
||||
|
||||
推荐导出数据格式为OpenAPI Spec,它是一种通用的 API 描述标准,Postman和APIFox都支持。
|
||||
|
||||
<img src="https://pic.bitday.top/i/2025/04/10/u48k7q-0.png" alt="image-20250410182110385" style="zoom:67%;" />
|
||||
|
||||
|
||||
|
||||
#### Swagger
|
||||
|
||||
1. 使得前后端分离开发更加方便,有利于团队协作
|
||||
|
||||
|
||||
179
自学/草稿.md
179
自学/草稿.md
@ -1,144 +1,67 @@
|
||||
下面从架构、扩展性、安全性、管理成本等几个维度,对 **Session** 和 **JWT** 进行对比,帮助你根据场景选择合适的方案。
|
||||
在 **0/1 背包问题**中,使用一维 DP 数组时**必须逆序遍历背包容量**,主要原因在于**避免同一物品被重复计算**。这与二维 DP 的实现方式有本质区别。下面通过公式和例子详细说明。
|
||||
|
||||
------
|
||||
---
|
||||
|
||||
## 一、基本原理
|
||||
## 为什么一维 DP 必须逆序遍历?
|
||||
|
||||
| 特性 | Session | JWT(JSON Web Token) |
|
||||
| -------- | ------------------------------------ | ----------------------------------------------- |
|
||||
| 存储方式 | 服务端存储会话数据(如内存、Redis) | 客户端存储完整的令牌(通常在 Header 或 Cookie) |
|
||||
| 标识方式 | 客户端持有一个 Session ID | 客户端持有一个自包含的 Token |
|
||||
| 状态管理 | 有状态(Stateful),服务器要维护会话 | 无状态(Stateless),服务器不存会话 |
|
||||
### 状态定义
|
||||
一维 DP 数组定义为:
|
||||
$$
|
||||
dp[j] = \text{背包容量为 } j \text{ 时的最大价值}
|
||||
$$
|
||||
|
||||
------
|
||||
### 状态转移方程
|
||||
对于物品 $i$(重量 $w_i$,价值 $v_i$):
|
||||
$$
|
||||
dp[j] = \max(dp[j], dp[j-w_i] + v_i) \quad (j \geq w_i)
|
||||
$$
|
||||
|
||||
## 二、对比分析
|
||||
### 关键问题
|
||||
- **正序遍历**会导致 $dp[j-w_i]$ 在更新 $dp[j]$ 时**已被当前物品更新过**,相当于重复使用该物品。
|
||||
- **逆序遍历**保证 $dp[j-w_i]$ 始终是**上一轮(未考虑当前物品)**的结果,符合 0/1 背包的“一次性”规则。
|
||||
|
||||
### 1. 架构与扩展性
|
||||
---
|
||||
|
||||
- **Session**
|
||||
- 单体应用:内存中维护 Map<sessionId, userData>,简单易用。
|
||||
- 分布式/集群:需要共享 Session(如 Redis、数据库、Sticky Session),增加运维成本。
|
||||
- **JWT**
|
||||
- 无状态:令牌自带用户信息及签名,服务器只需校验签名即可,无需存储。
|
||||
- 分布式友好:各节点只要共享签名密钥(或公钥),即可校验,无需集中存储。
|
||||
## 二维 DP 为何不需要逆序?
|
||||
|
||||
### 2. 性能
|
||||
二维 DP 定义为:
|
||||
$$
|
||||
dp[i][j] = \text{前 } i \text{ 个物品,容量 } j \text{ 时的最大价值}
|
||||
$$
|
||||
状态转移:
|
||||
$$
|
||||
dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w_i] + v_i)
|
||||
$$
|
||||
- 由于直接依赖 **上一行 $dp[i-1][\cdot]$**,不存在状态覆盖问题,正序/逆序均可。
|
||||
|
||||
- **Session**
|
||||
- 每次请求都要从存储(内存/Redis/DB)读取会话数据,IO 成本或网络开销。
|
||||
- 并发高时,集中式 Session 存储可能成为瓶颈。
|
||||
- **JWT**
|
||||
- 校验签名(HMAC 或 RSA)为 CPU 操作,无网络开销,性能开销较小。
|
||||
- 但 Token 通常更大(包含多段 Base64),每次请求都要传输,带宽略增。
|
||||
---
|
||||
|
||||
### 3. 安全性
|
||||
## 例子演示
|
||||
假设物品 $w=2$, $v=3$,背包容量 $C=5$。
|
||||
|
||||
- **Session**
|
||||
- 会话数据保存在服务器端,客户端只能拿到 Session ID,敏感数据不暴露。
|
||||
- 可在服务器端随时销毁或更新 Session(强制登出、权限变更即时生效)。
|
||||
- **JWT**
|
||||
- 令牌自包含所有声明(claims),如果存敏感数据需加密(JWE),否则仅签名(JWS)也可能泄露信息。
|
||||
- 无法主动撤销(除非做黑名单),需要控制有效期并结合“刷新令牌”机制。
|
||||
错误的正序遍历($j=2 \to 5$)
|
||||
|
||||
### 4. 可控性与管理
|
||||
1. $j=2$:
|
||||
$dp[2] = \max(0, dp[0]+3) = 3$
|
||||
$\Rightarrow dp = [0, 0, 3, 0, 0, 0]$
|
||||
2. $j=4$:
|
||||
$dp[4] = \max(0, dp[2]+3) = 6$
|
||||
$\Rightarrow$ **错误**:物品被重复使用两次!
|
||||
|
||||
- **Session**
|
||||
- **可控性强**:服务器可随时作废 Session,适合需要即时注销、权限动态调整的场景。
|
||||
- 过期策略灵活:可按用户、按应用统一配置。
|
||||
- **JWT**
|
||||
- **可控性弱**:Token 一旦签发,在到期前无法从服务器强制失效(除非额外维护黑名单)。
|
||||
- 需要设计“短生命周期 + 刷新令牌”模式,增加实现复杂度。
|
||||
### 正确的逆序遍历($j=5 \to 2$)
|
||||
1. $j=5$:
|
||||
$dp[5] = \max(0, dp[3]+3) = 0$ ($dp[3]$ 未更新)
|
||||
2. $j=2$:
|
||||
$dp[2] = \max(0, dp[0]+3) = 3$
|
||||
$\Rightarrow dp = [0, 0, 3, 3, 3, 0]$
|
||||
**正确**:物品仅使用一次。
|
||||
|
||||
### 5. 跨域与移动端
|
||||
---
|
||||
|
||||
- **Session**
|
||||
- 依赖 Cookie(同源策略),跨域或移动端(原生 App)使用受限。
|
||||
- 跨域时需配合 CORS + `withCredentials`,且浏览器必须支持并开启 Cookie。
|
||||
- **JWT**
|
||||
- 与 HTTP 协议无关,既可放在 Authorization 头,也可放在 URL、LocalStorage,移动端/第三方客户端更友好。
|
||||
- 只要客户端能发送 HTTP Header,就能携带 Token。
|
||||
## 总结
|
||||
| 维度 | 遍历顺序 | 原因 |
|
||||
| ------ | -------- | ------------------------------------------------------------ |
|
||||
| 一维DP | **逆序** | 防止 $dp[j-w_i]$ 被当前物品污染,确保每个物品只计算一次。 |
|
||||
| 二维DP | 任意顺序 | 状态分层存储($dp[i][j]$ 只依赖 $dp[i-1][\cdot]$),无覆盖风险。 |
|
||||
|
||||
### 6. 实现复杂度
|
||||
|
||||
- **Session**
|
||||
- 框架通常开箱即用(如 Spring Session),开发者只需开启即可。
|
||||
- 自动处理过期、失效,管理简单。
|
||||
- **JWT**
|
||||
- 需要设计签名算法、密钥管理、过期策略、刷新机制、黑名单等。
|
||||
- 容易因配置不当造成安全漏洞(算法降级、密钥泄露、Token 劫持等)。
|
||||
|
||||
------
|
||||
|
||||
## 三、何时选用
|
||||
|
||||
| 场景类型 | 推荐方案 | 原因 |
|
||||
| --------------------------- | -------- | ---------------------------------------------------------- |
|
||||
| 单体 Web 应用、后台管理系统 | Session | 简单、可控、安全性高,框架支持完善。 |
|
||||
| 分布式微服务、无状态 API | JWT | 无需集中存储,易扩展;移动端/第三方客户端友好。 |
|
||||
| 高度安全、需即时失效场景 | Session | 可随时在服务器端销毁会话,确保强制登出或权限变更即时生效。 |
|
||||
| 跨域或多端(Web + App) | JWT | Token 可在多种客户端轻松传递,无需依赖浏览器 Cookie。 |
|
||||
|
||||
------
|
||||
|
||||
## 四、示例代码
|
||||
|
||||
### Session 示例(Spring Boot)
|
||||
|
||||
```java
|
||||
// 登录时创建 Session
|
||||
@PostMapping("/login")
|
||||
public String login(HttpServletRequest req, @RequestParam String user, @RequestParam String pass) {
|
||||
if (authService.verify(user, pass)) {
|
||||
req.getSession().setAttribute("userId", user);
|
||||
return "登录成功";
|
||||
}
|
||||
return "登录失败";
|
||||
}
|
||||
|
||||
// 受保护资源
|
||||
@GetMapping("/profile")
|
||||
public User profile(HttpServletRequest req) {
|
||||
String userId = (String) req.getSession().getAttribute("userId");
|
||||
return userService.findById(userId);
|
||||
}
|
||||
```
|
||||
|
||||
### JWT 示例(Spring Boot + jjwt)
|
||||
|
||||
```java
|
||||
// 生成 Token
|
||||
@PostMapping("/login")
|
||||
public String login(@RequestParam String user, @RequestParam String pass) {
|
||||
if (authService.verify(user, pass)) {
|
||||
return Jwts.builder()
|
||||
.setSubject(user)
|
||||
.setExpiration(new Date(System.currentTimeMillis() + 3600_000))
|
||||
.signWith(SignatureAlgorithm.HS256, secretKey)
|
||||
.compact();
|
||||
}
|
||||
throw new UnauthorizedException();
|
||||
}
|
||||
|
||||
// 过滤器中校验
|
||||
@Override
|
||||
protected void doFilterInternal(HttpServletRequest req, HttpServletResponse res, FilterChain chain) {
|
||||
String token = req.getHeader("Authorization");
|
||||
if (token != null && token.startsWith("Bearer ")) {
|
||||
String user = Jwts.parser().setSigningKey(secretKey)
|
||||
.parseClaimsJws(token.substring(7))
|
||||
.getBody().getSubject();
|
||||
// 将 user 存入 SecurityContext …
|
||||
}
|
||||
chain.doFilter(req, res);
|
||||
}
|
||||
```
|
||||
|
||||
------
|
||||
|
||||
## 五、结论
|
||||
|
||||
- **Session**:上手简单、安全可控,适合绝大多数传统 Web 应用。
|
||||
- **JWT**:更灵活、易扩展,适合分布式架构、多端场景,但需要更复杂的设计与安全防护。
|
||||
|
||||
根据你的项目架构、团队经验和安全需求,选择最合适的方案即可。
|
||||
**核心思想**:一维 DP 的空间优化需要逆序来保证状态的**无后效性**。
|
||||
Loading…
x
Reference in New Issue
Block a user