md_files/科研/线性代数.md

线性代数

线性变换

每列代表一个基向量，行数代码这个基向量所张成空间的维度，二行三列表示二维空间的三个基向量。

• 二维标准基矩阵（单位矩阵）：

  
  \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | \\ \mathbf{i} & \mathbf{j} \\ | & | \end{bmatrix}
  

• 三维标准基矩阵（单位矩阵）：

  
  \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{i} & \mathbf{j} & \mathbf{k} \\ | & | & | \end{bmatrix}
  

矩阵乘向量

在 3blue1brown 的“线性代数的本质”系列中，他把矩阵乘向量的运算解释为线性组合和线性变换的过程。具体来说：

• 计算方法
  给定一个 m \times n 的矩阵 A 和一个 n 维向量 $ \mathbf{x} = [x_1, x_2, \dots, x_n]^T $，矩阵与向量的乘积可以表示为：

  
  A\mathbf{x} = x_1 \mathbf{a}_1 + x_2 \mathbf{a}_2 + \cdots + x_n \mathbf{a}_n
  

  其中，\mathbf{a}_i 表示 A 的第 i 列向量。也就是说，我们用向量 \mathbf{x} 的各个分量作为权重，对矩阵的各列进行线性组合。

  例如：矩阵 A 是一个二阶矩阵：

  
  A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
  

  向量 \mathbf{x} 是一个二维列向量：

  
  \mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix}
  

  可以将这个乘法看作是用 x 和 y 这两个数，分别对矩阵的两列向量进行加权：

  
  A\mathbf{x} = x \cdot \begin{bmatrix} a \\ c \end{bmatrix} + y \cdot \begin{bmatrix} b \\ d \end{bmatrix}
  

  也就是说，矩阵乘向量的结果，是“矩阵每一列”乘以“向量中对应的分量”，再把它们加起来。

• 背后的思想

  1. 分解为基向量的组合：
     任何向量都可以看作是标准基向量的线性组合。矩阵 A 在几何上代表了一个线性变换，而标准基向量在这个变换下会分别被映射到新的位置，也就是矩阵的各列。

  2. 构造变换：
     当我们用 \mathbf{x} 的分量对这些映射后的基向量加权求和时，就得到了 \mathbf{x} 在变换后的结果。这种方式不仅方便计算，而且直观地展示了线性变换如何“重塑”空间——每一列告诉我们基向量被如何移动，然后这些移动按比例组合出最终向量的位置。

矩阵乘矩阵

当你有两个矩阵 A 和 $ B ，矩阵乘法 AB $ 实际上代表的是：

先对向量应用 B 的线性变换，再应用 A 的线性变换。

也就是说：

(AB)\vec{v} = A(B\vec{v})

3blue1brown 的直觉解释：

矩阵 B：提供了新的变换后基向量

记住：矩阵的每一列，表示标准基向量 \mathbf{e}_1, \mathbf{e}_2 在变换后的样子。

所以：

• B 是一个变换，它把空间“拉伸/旋转/压缩”成新的形状；
• A 接着又对这个已经变形的空间进行变换。

例：

A = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}

• B 的列是：
  • \begin{bmatrix} 1 \\ 1 \end{bmatrix} → 第一个标准基向量变形后的位置
  • \begin{bmatrix} -1 \\ 1 \end{bmatrix} → 第二个标准基向量变形后的位置

我们计算：

• A \cdot \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}
• A \cdot \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}

所以：

AB = \begin{bmatrix} 2 & -2 \\ 3 & 3 \end{bmatrix}

这个新矩阵 AB 的列向量，表示标准基向量在经历了 “先 B 再 A” 的变换后，落在了哪里。

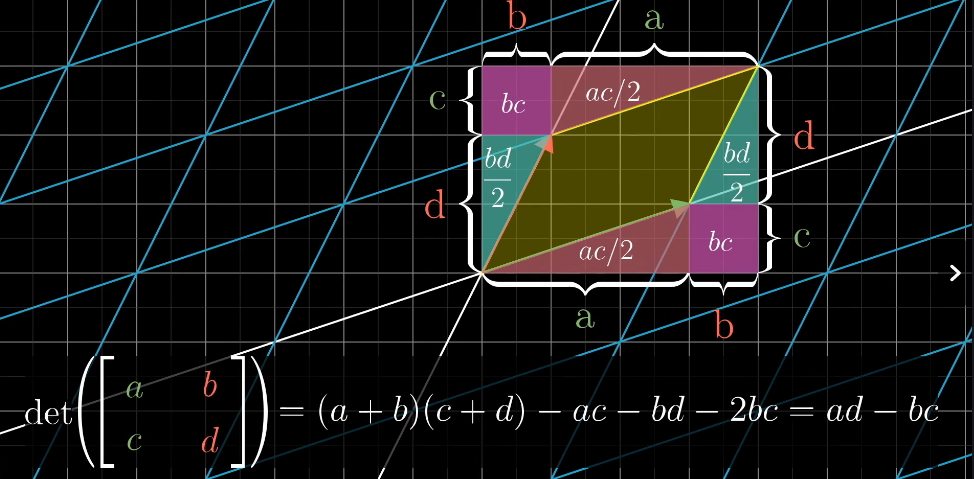
行列式

3blue1brown讲解行列式时，核心在于用几何直观来理解行列式的意义：

缩放比例！！！

体积（或面积）的伸缩因子 对于二维空间中的2×2矩阵，行列式的绝对值表示该矩阵作为线性变换时，对单位正方形施加变换后得到的平行四边形的面积。类似地，对于三维空间中的3×3矩阵，行列式的绝对值就是单位立方体变换后的平行六面体的体积。也就是说，行列式告诉我们这个变换如何“拉伸”或“压缩”空间。

方向的指示（有向面积或体积） 行列式不仅仅给出伸缩倍数，还通过正负号反映了变换是否保持了原来的方向（正）还是发生了翻转（负）。例如，在二维中，如果行列式为负，说明变换过程中存在翻转（类似镜像效果）。

变换的可逆性 当行列式为零时，说明该线性变换把空间压缩到了低维（例如二维变一条线，三维变成一个平面或线），这意味着信息在变换过程中丢失，变换不可逆。

逆矩阵、列空间、零空间

逆矩阵

逆矩阵描述了一个矩阵所代表的线性变换的**“反过程”**。假设矩阵 A 对空间做了某种变换（比如旋转、拉伸或压缩），那么 A^{-1} 就是把这个变换“逆转”，把变换后的向量再映射回原来的位置。

前提是A 是可逆的，即它对应的变换不会把空间压缩到更低的维度。

秩

秩等于矩阵列向量（或行向量）所生成的空间的维数。例如，在二维中，如果一个 2 \times 2 矩阵的秩是 2，说明这个变换把平面“充满”；如果秩为 1，则所有输出都落在一条直线上，说明变换“丢失”了一个维度。

列空间

列空间是矩阵所有列向量的线性组合所构成的集合（也可以说所有可能的输出向量$A\mathbf{x}$所构成的集合）。 比如一个二维变换的列空间可能是整个平面，也可能只是一条直线，这取决于矩阵的秩。

零空间

零空间（又称核、kernel）是所有在该矩阵作用（线性变换$A$）下变成零向量的输入向量的集合。

它展示了变换中哪些方向被“压缩”成了一个点（原点）。例如，在三维中，如果一个矩阵将所有向量沿某个方向压缩到零，那么这个方向构成了零空间。

零空间解释了$Ax=0$的解的集合，就是齐次的通解。如果满秩，零空间只有唯一解零向量。

求解线性方程

设线性方程组写作

A\mathbf{x} = \mathbf{b}

这相当于在问：“有没有一个向量 \mathbf{x} ，它经过矩阵 A 的变换后，恰好落在 \mathbf{b} 所在的位置？”

• 如果 \mathbf{b} 落在 A 的列空间内，那么就存在解。解可能是唯一的（当矩阵满秩时）或无穷多（当零空间非平凡时）。
• 如果 \mathbf{b} 不在列空间内，则说明 \mathbf{b} 不可能由 A 的列向量线性组合得到，这时方程组无解。
• 唯一解对应于所有这些几何对象在一点相交；
• 无限多解对应于它们沿着某个方向重合；
• 无解则说明这些对象根本没有公共交点。

基变换

新基下的变换矩阵 A_C 为：

A_C = P^{-1} A P

$P$：从原基到新基的基变换矩阵（可逆），$P$的每一列代表了新基中的一个基向量

$A$：线性变换 T 在原基下的矩阵表示

原来空间中进行$A$线性变换等同于新基的视角下进行 A_C 变换

点积、哈达马积

向量点积（Dot Product）

3blue1brown认为，两个向量的点乘就是将其中一个向量转为线性变换。

假设有两个向量

\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}, \quad \mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}.

\mathbf{v} \cdot \mathbf{w} =\begin{bmatrix} v_1 & v_2 \end{bmatrix}\begin{bmatrix} w_1 \\ w_2 \end{bmatrix}=v_1w_1 + v_2w_2..

• 结果：
  点积的结果是一个标量（即一个数）。
• 几何意义：
  点积可以衡量两个向量的相似性，或者计算一个向量在另一个向量方向上的投影。

哈达马积（Hadamard Product）

• 定义：
  对于两个向量 \mathbf{u} = [u_1, u_2, \dots, u_n] 和 $\mathbf{v} = [v_1, v_2, \dots, v_n]$，它们的哈达马积定义为：

  
  \mathbf{u} \circ \mathbf{v} = [u_1 v_1, u_2 v_2, \dots, u_n v_n].
  

• 结果：
  哈达马积的结果是一个向量，其每个分量是对应位置的分量相乘。

• 几何意义：
  哈达马积通常用于逐元素操作，比如在神经网络中对两个向量进行逐元素相乘。

矩阵也有哈达马积！。

特征值和特征向量

设矩阵：

A = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}

步骤 1：求特征值

构造特征方程：

\det(A - \lambda I) = \det\begin{bmatrix} 2-\lambda & 1 \\ 0 & 3-\lambda \end{bmatrix} = (2-\lambda)(3-\lambda) - 0 = 0

解得：

(2-\lambda)(3-\lambda) = 0 \quad \Longrightarrow \quad \lambda_1 = 2,\quad \lambda_2 = 3

步骤 2：求特征向量

• 对于 $\lambda_1 = 2$： 解方程：

  (A - 2I)\mathbf{x} = \begin{bmatrix} 2-2 & 1 \\ 0 & 3-2 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_2 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}

从第一行 $x_2 = 0$。因此特征向量可以写成：

  \mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad (\text{任意非零常数倍})

• 对于 $\lambda_2 = 3$： 解方程：

  (A - 3I)\mathbf{x} = \begin{bmatrix} 2-3 & 1 \\ 0 & 3-3 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -x_1+x_2 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}

从第一行得 -x_1 + x_2 = 0 或 $x_2 = x_1$。因此特征向量可以写成：

  \mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \quad (\text{任意非零常数倍})

设一个对角矩阵：

D = \begin{bmatrix} d_1 & 0 \\ 0 & d_2 \end{bmatrix}

\lambda_1 = d_1,\quad \lambda_2 = d_2

对角矩阵的特征方程为：

\det(D - \lambda I) = (d_1 - \lambda)(d_2 - \lambda) = 0

因此特征值是：

\lambda_1 = d_1,\quad \lambda_2 = d_2

• 对于 $\lambda_1 = d_1$，方程 (D-d_1I)\mathbf{x}=\mathbf{0} 得到：

  \begin{bmatrix} 0 & 0 \\ 0 & d_2-d_1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ (d_2-d_1)x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}

若 $d_1 \neq d_2$，则必须有 $x_2=0$，而 x_1 可任意取非零值，因此特征向量为：

  \mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}

• 对于 $\lambda_2 = d_2$，类似地解得：

  \mathbf{v}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix}

矩阵乘法

全连接神经网络

其中：

• a^{(0)} 是输入向量，表示当前层的输入。

• \mathbf{W} 是权重矩阵，表示输入向量到输出向量的线性变换。

• b 是偏置向量，用于调整输出。

• \sigma 是激活函数（如 ReLU、Sigmoid 等），用于引入非线性。

• 输入向量 $a^{(0)}$：

  a^{(0)} = \begin{pmatrix}
  a_0^{(0)} \\
  a_1^{(0)} \\
  \vdots \\
  a_n^{(0)}
  \end{pmatrix}

这是一个 n+1 维的列向量，表示输入特征。

• 权重矩阵 $\mathbf{W}$：

  \mathbf{W} = \begin{pmatrix}
  w_{0,0} & w_{0,1} & \cdots & w_{0,n} \\
  w_{1,0} & w_{1,1} & \cdots & w_{1,n} \\
  \vdots & \vdots & \ddots & \vdots \\
  w_{k,0} & w_{k,1} & \cdots & w_{k,n} \\
  \end{pmatrix}

这是一个 k \times (n+1) 的矩阵，其中 k 是输出向量的维度，n+1 是输入向量的维度。

• 偏置向量 $b$：

  b = \begin{pmatrix}
  b_0 \\
  b_1 \\
  \vdots \\
  b_k
  \end{pmatrix}

这是一个 k 维的列向量，用于调整输出。

1. 在传统的连续时间 RNN 写法里，常见的是

   \sum_{j} W_{ij} \, \sigma(x_j),

这代表对所有神经元 j 的激活 \sigma(x_j) 做加权求和，再求和到神经元 $i$。

如果拆开来看，每个输出分量也都含一个求和 $\sum_{j}$：

• 输出向量的第 1 个分量（记作第 1 行的结果）：

     (W_r x)_1 = 0.3 \cdot x_1 + (-0.5) \cdot x_2 = 0.3 \cdot 2 + (-0.5) \cdot 1 = 0.6 - 0.5 = 0.1.

• 输出向量的第 2 个分量（第 2 行的结果）：

     (W_r x)_2 = 1.2 \cdot x_1 + 0.4 \cdot x_2 = 1.2 \cdot 2 + 0.4 \cdot 1 = 2.4 + 0.4 = 2.8.

2. 在使用矩阵乘法时，你可以写成

   y = W_r \, \sigma(x),

其中 \sigma 表示对 x 的各分量先做激活，接着用 W_r 乘上去。这就是把“$\sum_j \dots$”用矩阵乘法隐藏了。

\begin{pmatrix}
0.3 & -0.5\\
1.2 & \;\,0.4
\end{pmatrix}
\begin{pmatrix}
2\\
1
\end{pmatrix}
=
\begin{pmatrix}
0.3 \times 2 + (-0.5) \times 1\\[6pt]
1.2 \times 2 + 0.4 \times 1
\end{pmatrix}
=
\begin{pmatrix}
0.6 - 0.5\\
2.4 + 0.4
\end{pmatrix}
=
\begin{pmatrix}
0.1\\
2.8
\end{pmatrix}.

奇异值

定义

对于一个 m \times n 的矩阵 $A$，其奇异值是非负实数 $\sigma_1, \sigma_2, \ldots, \sigma_r$（$r = \min(m, n)$），满足存在正交矩阵 U 和 $V$，使得：

A = U \Sigma V^T

其中，\Sigma 是对角矩阵，对角线上的元素即为奇异值。

---

主要特点

1. 非负性：奇异值总是非负的。
2. 对角矩阵的奇异值是对角线元素的绝对值。
3. 降序排列：通常按从大到小排列，即 $\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_r \geq 0$。
4. 矩阵分解：奇异值分解（SVD）将矩阵分解为三个矩阵的乘积，U 和 V 是正交矩阵，\Sigma 是对角矩阵。
5. 应用广泛：奇异值在数据降维、噪声过滤、图像压缩等领域有广泛应用。

---

奇异值求解

奇异值可以通过计算矩阵 A^T A 或 A A^T 的特征值的平方根得到。

步骤 1：计算 $A^T A$

首先，我们计算矩阵 A 的转置 $A^T$：

A^T = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix}

然后，计算 $A^T A$：

A^T A = \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} \begin{pmatrix} 3 & 0 \\ 0 & -4 \end{pmatrix} = \begin{pmatrix} 9 & 0 \\ 0 & 16 \end{pmatrix}

步骤 2：计算 A^T A 的特征值

接下来，我们计算 A^T A 的特征值。特征值 \lambda 满足以下特征方程：

\det(A^T A - \lambda I) = 0

即：

\det \begin{pmatrix} 9 - \lambda & 0 \\ 0 & 16 - \lambda \end{pmatrix} = (9 - \lambda)(16 - \lambda) = 0

解这个方程，我们得到两个特征值：

\lambda_1 = 16, \quad \lambda_2 = 9

步骤 3：计算奇异值

奇异值是特征值的平方根，因此我们计算：

\sigma_1 = \sqrt{\lambda_1} = \sqrt{16} = 4

\sigma_2 = \sqrt{\lambda_2} = \sqrt{9} = 3

结果

矩阵 A 的奇异值为 4 和 3。

奇异值分解

给定一个实矩阵 $A$（形状为 $m \times n$），SVD 是将它分解为：

A = U \Sigma V^T

1. 构造 $A^T A$

   • 计算对称矩阵 $A^T A$（$n \times n$）

2. 求解 A^T A 的特征值和特征向量

   • 设特征值为 \lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_n \geq 0
   • 对应特征向量为 \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n

3. 计算奇异值

   • \sigma_i = \sqrt{\lambda_i}

4. 构造矩阵 $V$

   • 将正交归一的特征向量作为列向量：V = [\mathbf{v}_1 | \mathbf{v}_2 | \dots | \mathbf{v}_n]

5. 求矩阵 $U$

   • 对每个非零奇异值：\mathbf{u}_i = \frac{A \mathbf{v}_i}{\sigma_i}
   • 标准化（保证向量长度为 1）后组成 U = [\mathbf{u}_1 | \mathbf{u}_2 | \dots | \mathbf{u}_m]

6. 构造 $\Sigma$

   • 对角线放置奇异值：$\Sigma = \text{diag}(\sigma_1, \sigma_2, \dots, \sigma_p)$，p=\min(m,n)

范数

L2范数定义：

对于一个向量 $\mathbf{w} = [w_1, w_2, \dots, w_n]$，L2 范数定义为

\|\mathbf{w}\|_2 = \sqrt{w_1^2 + w_2^2 + \dots + w_n^2}

假设一个权重向量为 $\mathbf{w} = [3, -4]$，则

\|\mathbf{w}\|_2 = \sqrt{3^2 + (-4)^2} = \sqrt{9+16} = \sqrt{25} = 5.

用途：

• 正则化（L2正则化/权重衰减）：在训练过程中，加入 L2 正则项有助于防止模型过拟合。正则化项通常是权重的 L2 范数的平方，例如

  \lambda \|\mathbf{w}\|_2^2

其中 \lambda 是正则化系数。

• 梯度裁剪：在 RNN 等深度网络中，通过计算梯度的 L2 范数来判断是否需要对梯度进行裁剪，从而防止梯度爆炸。

具体例子：

假设我们有一个简单的线性回归模型，损失函数为均方误差（MSE）：

L(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2

其中，N 是样本数量，y_i 是第 i 个样本的真实值，\mathbf{x}_i 是第 i 个样本的特征向量，\mathbf{w} 是权重向量。

加入 L2 正则项后，新的损失函数为：

L_{\text{reg}}(\mathbf{w}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \mathbf{w}^T \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_2^2

在训练过程中，优化算法会同时最小化原始损失函数和正则项，从而在拟合训练数据的同时，避免权重值过大。

梯度更新

在梯度下降算法中，权重 \mathbf{w} 的更新公式为：

\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla L_{\text{reg}}(\mathbf{w})

其中，\eta 是学习率，\nabla L_{\text{reg}}(\mathbf{w}) 是损失函数关于 \mathbf{w} 的梯度。

对于加入 L2 正则项的损失函数，梯度为：

\nabla L_{\text{reg}}(\mathbf{w}) = \nabla L(\mathbf{w}) + 2\lambda \mathbf{w}

因此，权重更新公式变为：

\mathbf{w} \leftarrow \mathbf{w} - \eta (\nabla L(\mathbf{w}) + 2\lambda \mathbf{w})

通过加入 L2 正则项，模型在训练过程中不仅会最小化原始损失函数，还会尽量减小权重的大小，从而避免过拟合。正则化系数 \lambda 控制着正则化项的强度，较大的 \lambda 会导致权重更小，模型更简单，但可能会欠拟合；较小的 \lambda 则可能无法有效防止过拟合。因此，选择合适的 \lambda 是使用 L2 正则化的关键。

矩阵的元素级范数

L0范数（但它 并不是真正的范数）：

\|A\|_0 = \text{Number of non-zero elements in } A = \sum_{i=1}^{m} \sum_{j=1}^{n} \mathbb{I}(a_{ij} \neq 0)

其中：

• \mathbb{I}(\cdot) 是指示函数（若 a_{ij} \neq 0 则取 1，否则取 0）。
• 如果矩阵 A 有 k 个非零元素，则 $|A|_0 = k$。

1. 衡量稀疏性：

   • \|A\|_0 越小，矩阵 A 越稀疏（零元素越多）。
   • 在压缩感知、低秩矩阵恢复、稀疏编码等问题中，常用 L_0 范数来 约束解的稀疏性。

2. 非凸、非连续、NP难优化：

   • L_0 范数是 离散的，导致优化问题通常是 NP难 的（无法高效求解）。

   • 因此，实际应用中常用 L_1 范数（绝对值之和）作为凸松弛替代：

     
     \|A\|_1 = \sum_{i,j} |a_{ij}|
     

NP难问题：

可以在多项式时间内 验证一个解是否正确，但 不一定能在多项式时间内找到解。

L1范数：元素绝对值和

\|A\|_1 = \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|

范数类型	定义	性质	优化难度	用途
$L_0$	\sum_{i,j} \mathbb{I}(a_{ij} \neq 0)	非凸、离散、不连续	NP难	精确稀疏性控制
$L_1$	$\sum_{i,j}	a_{ij}	$	凸、连续

矩阵的核范数

核范数，又称为迹范数（trace norm），是矩阵范数的一种，定义为矩阵所有奇异值之和。对于一个矩阵 $A$（假设其奇异值为 $\sigma_1, \sigma_2, \dots, \sigma_r$），其核范数定义为：

\|A\|_* = \sum_{i=1}^{r} \sigma_i,

其中 r 是矩阵 A 的秩。

核范数的主要特点

1. 凸性

   • 核范数是一个凸函数，因此在优化问题中常用作替代矩阵秩的惩罚项（因为直接最小化矩阵秩是一个NP困难的问题）。

2. 低秩逼近

   • 在矩阵补全、低秩矩阵恢复等应用中，核范数被用来鼓励矩阵解具有低秩性质，因其是矩阵秩的凸松弛。

3. 与SVD的关系

   • 核范数直接依赖于矩阵的奇异值，计算时通常需要奇异值分解（SVD）。

Frobenius 范数

对于一个矩阵 $A \in \mathbb{R}^{m \times n}$，其 Frobenius 范数定义为

\|A\|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} a_{ij}^2}

这个定义与向量 L2 范数类似，只不过是对矩阵中所有元素取平方和后再开平方。

对于归一化的向量\mathbf{x}_m ，其外积矩阵 $\mathbf{x}_m \mathbf{x}_m^T$，其元素为 $(\mathbf{x}_m \mathbf{x}m^T){ij} = x_i x_j$，因此：

\|\mathbf{x}_m \mathbf{x}_m^T\|_F = \sqrt{\sum_{i=1}^n \sum_{j=1}^n |x_i x_j|^2 } = \sqrt{\left( \sum_{i=1}^n x_i^2 \right) \left( \sum_{j=1}^n x_j^2 \right) } = \|\mathbf{x}_m\|_2 \cdot \|\mathbf{x}_m\|_2 = 1.

例：

设归一化向量 $\mathbf{x} = \begin{bmatrix} \frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} \end{bmatrix}$，其外积矩阵为：

\mathbf{x} \mathbf{x}^T = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}

计算 Frobenius 范数：

\|\mathbf{x} \mathbf{x}^T\|_F = \sqrt{ \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 } = \sqrt{4 \cdot \frac{1}{4}} = 1.

---

如果矩阵 A 的奇异值为 $\sigma_1, \sigma_2, \ldots, \sigma_n$，则：

\|A\|_F = \sqrt{\sum_{i=1}^n \sigma_i^2}

这使得 Frobenius 范数在低秩近似和矩阵分解（如 SVD）中非常有用。

设矩阵 A 为：

A = \begin{bmatrix}
1 & 0 \\
0 & 2 \\
1 & 1
\end{bmatrix}

定义：

\|A\|_F = \sqrt{1^2 + 0^2 + 0^2 + 2^2 + 1^2 + 1^2 } = \sqrt{1 + 0 + 0 + 4 + 1 + 1} = \sqrt{7}

验证：

1. 计算 $A^T A$：

   
   A^T A = \begin{bmatrix}
   1 & 0 & 1 \\
   0 & 2 & 1
   \end{bmatrix}
   \begin{bmatrix}
   1 & 0 \\
   0 & 2 \\
   1 & 1
   \end{bmatrix} = \begin{bmatrix}
   2 & 1 \\
   1 & 5
   \end{bmatrix}
   

2. 求 A^T A 的特征值（即奇异值的平方）：

   
   \det(A^T A - \lambda I) = \lambda^2 - 7\lambda + 9 = 0 \implies \lambda = \frac{7 \pm \sqrt{13}}{2}
   

   因此：

   
   \sigma_1 = \sqrt{\frac{7 + \sqrt{13}}{2}}, \quad \sigma_2 = \sqrt{\frac{7 - \sqrt{13}}{2}}
   

3. 验证 Frobenius范数：

   
   \sigma_1^2 + \sigma_2^2 = \frac{7 + \sqrt{13}}{2} + \frac{7 - \sqrt{13}}{2} = 7
   

   所以：

   
   \|A\|_F = \sqrt{7}
   

公式正确！

迹和 Frobenius 范数的关系：

\|A\|_F^2 = \text{tr}(A^* A)

这表明 Frobenius 范数的平方就是 A^* A 所有特征值之和。而 A^* A 的特征值开方就是A的奇异值。

最大范数

矩阵的最大范数（也称为 元素级无穷范数 或 一致范数）定义为矩阵所有元素绝对值的最大值：

\|A\|_{\max} = \max_{i,j} |A_{ij}|

它衡量的是矩阵中绝对值最大的元素，适用于逐元素（element-wise）分析。

如果比较两个矩阵 A 和 $B$，它们的误差矩阵 E = A - B 的最大范数为：

\|A - B\|_{\max} = \max_{i,j} |A_{ij} - B_{ij}|

意义：

• 如果 $|A - B|_{\max} \leq \epsilon$，说明 A 和 B 的所有对应元素的误差都不超过 $\epsilon$。

对于任意 m \times n 的矩阵 $A$，以下不等式成立：

\|A\|_{\max} \leq \|A\|_F \leq \sqrt{mn} \cdot \|A\|_{\max}

矩阵的迹

迹的定义

对于一个 n \times n 的矩阵 $B$，其迹（trace）定义为矩阵对角线元素之和：

\text{tr}(B) = \sum_{i=1}^n B_{ii}

迹与特征值的关系

对于一个 n \times n 的矩阵 $B$，其迹等于其特征值之和。即：

\text{tr}(B) = \sum_{i=1}^n \lambda_i

其中 \lambda_1, \lambda_2, \ldots, \lambda_n 是矩阵 B 的特征值。

应用到 $A^ A$*

对于矩阵 $A^* A$（如果 A 是实矩阵，则 $A^* = A^T$），它是一个半正定矩阵，其特征值是非负实数。

A^* A 的迹还与矩阵 A 的 Frobenius 范数有直接关系。具体来说：

\|A\|_F^2 = \text{tr}(A^* A)

迹的基本性质

迹是一个线性运算，即对于任意标量 c_1, c_2 和矩阵 $A, B$，有：

\text{tr}(c_1 A + c_2 B) = c_1 \text{tr}(A) + c_2 \text{tr}(B)

对于任意矩阵 $A, B, C$，迹满足循环置换性质：

\text{tr}(ABC) = \text{tr}(CAB) = \text{tr}(BCA)

注意：迹的循环置换性不意味着 $\text{tr}(ABC) = \text{tr}(BAC)$，除非矩阵 A, B, C 满足某些特殊条件（如对称性）。

酉矩阵

酉矩阵是一种复矩阵，其满足下面的条件：对于一个 n \times n 的复矩阵 $U$，如果有

U^* U = U U^* = I,

其中 U^* 表示 U 的共轭转置（先转置再取复共轭），而 I 是 n \times n 的单位矩阵，那么 U 就被称为酉矩阵。简单来说，酉矩阵在复内积空间中保持内积不变，相当于在该空间中的“旋转”或“反射”。

如果矩阵的元素都是实数，那么 U^* 就等于 $U^T$（转置），这时酉矩阵就退化为正交矩阵。

考虑二维旋转矩阵

U = \begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}.

当 \theta 为任意实数时，这个矩阵满足

U^T U = I,

所以它是一个正交矩阵，同时也属于酉矩阵的范畴。

例如，当 $\theta = \frac{\pi}{4}$（45°）时，

U = \begin{bmatrix}
\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}
\end{bmatrix}.

正定\正半定矩阵

1. 正定矩阵（PD）

   
   A \text{ 正定} \iff \forall\, x \in \mathbb{R}^n \setminus \{0\}, \quad x^T A x > 0.
   

2. 正半定矩阵（PSD）

   
   A \text{ 正半定} \iff \forall\, x \in \mathbb{R}^n, \quad x^T A x \ge 0.
   

• PD：所有特征值都严格大于零。
  $\lambda_i(A)>0,;i=1,\dots,n$。

• PSD：所有特征值都非负。
  $\lambda_i(A)\ge0,;i=1,\dots,n$。

拉普拉斯矩阵是正半定矩阵！

对于任意实矩阵 $A$（大小为 $m\times n$），矩阵 $B = A^T A\quad(\text{大小为 }n\times n).$是半正定矩阵

• 显然

  
  B^T = (A^T A)^T = A^T (A^T)^T = A^T A = B,
  

  所以 B 是对称矩阵。

• 对任意向量 $x\in\mathbb R^n$，有

  
  x^T B\,x = x^T (A^T A) x = (Ax)^T (Ax) = \|Ax\|^2 \;\ge\;0.
  

  因此 B 总是 正半定（PSD） 的。

对称非负矩阵分解

A≈HH^T

1. 问题回顾

给定一个对称非负矩阵 $A\in\mathbb{R}^{n\times n}$，我们希望找到一个非负矩阵 H\in\mathbb{R}^{n\times k} 使得

A \approx HH^T.

为此，我们可以最小化目标函数(损失函数)

f(H)=\frac{1}{2}\|A-HH^T\|_F^2,

其中 \|\cdot\|_F 表示 Frobenius 范数，定义为矩阵所有元素的平方和的平方根。

\| A - H H^T \|_F^2 表示矩阵 A - H H^T 的所有元素的平方和。

2. 梯度下降方法

2.1 计算梯度

目标函数(损失函数)是

f(H)=\frac{1}{2}\|A-HH^T\|_F^2.

\|M\|_F^2 = \operatorname{trace}(M^T M),

因此，目标函数可以写成：

f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^T\bigl(A-HH^T\bigr)\Bigr].

注意到 A 和HH^T 都是对称矩阵，可以简化为：

f(H)=\frac{1}{2}\operatorname{trace}\Bigl[\bigl(A-HH^T\bigr)^2\Bigr].

展开后得到

f(H)=\frac{1}{2}\operatorname{trace}\Bigl[A^2 - 2AHH^T + (HH^T)^2\Bigr].

其中 \operatorname{trace}(A^2) 与 H 无关，可以看作常数，不影响梯度计算。

计算 \nabla_H \operatorname{trace}(-2 A H H^T)

\nabla_H \operatorname{trace}(-2 A H H^T) = -4 A H

计算 \nabla_H \operatorname{trace}((H H^T)^2)

\nabla_H \operatorname{trace}((H H^T)^2) = 4 H H^T H

将两部分梯度合并：

\nabla_H f(H) = \frac{1}{2}(4 H H^T H - 4 A H )= 2(H H^T H - A H)

2.2 梯度下降更新

设学习率为 $\eta>0$，则梯度下降的基本更新公式为：

H \leftarrow H - \eta\, \nabla_H f(H) = H - 2\eta\Bigl(HH^T H - A H\Bigr).

由于我们要求 H 中的元素保持非负，所以每次更新之后通常需要进行投影：

H_{ij} \leftarrow \max\{0,\,H_{ij}\}.

这种方法称为投影梯度下降，保证每一步更新后 H 满足非负约束。

3. 举例说明

设对称非负矩阵：

A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}, \quad k=1, \quad H \in \mathbb{R}^{2 \times 1}

初始化 $H^{(0)} = \begin{bmatrix} 1 \ 1 \end{bmatrix}$，学习率 $\eta = 0.01$。

迭代步骤：

1. 初始 H^{(0)}:

   H^{(0)} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}, \quad H^{(0)}(H^{(0)})^T = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}.

目标函数值：

   f(H^{(0)}) = \frac{1}{2} \left( (2-1)^2 + 2(1-1)^2 + (2-1)^2 \right) = 1.

2. 计算梯度：

   HH^T H = \begin{bmatrix} 2 \\ 2 \end{bmatrix}, \quad AH = \begin{bmatrix} 3 \\ 3 \end{bmatrix},

   \nabla_H f(H^{(0)}) = 2 \left( \begin{bmatrix} 2 \\ 2 \end{bmatrix} - \begin{bmatrix} 3 \\ 3 \end{bmatrix} \right) = \begin{bmatrix} -2 \\ -2 \end{bmatrix}.

3. 更新 H:

   H^{(1)} = H^{(0)} - 2 \cdot 0.01 \cdot \begin{bmatrix} -2 \\ -2 \end{bmatrix} = \begin{bmatrix} 1.04 \\ 1.04 \end{bmatrix}.

4. 更新后目标函数：

   H^{(1)}(H^{(1)})^T = \begin{bmatrix} 1.0816 & 1.0816 \\ 1.0816 & 1.0816 \end{bmatrix},

   f(H^{(1)}) = \frac{1}{2} \left( (2-1.0816)^2 + 2(1-1.0816)^2 + (2-1.0816)^2 \right) \approx 0.8464.

一次迭代后目标函数值从 1.0 下降至 0.8464