zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity
md_files/科研/图神经网络.md

20 KiB
Raw Blame History

图神经网络

图表示学习的本质是把节点映射成低维连续稠密的向量。这些向量通常被称为 嵌入（Embedding），它们能够捕捉节点在图中的结构信息和属性信息，从而用于下游任务（如节点分类、链接预测、图分类等）。

  • 低维：将高维的原始数据（如邻接矩阵或节点特征）压缩为低维向量，减少计算和存储开销。
  • 连续：将离散的节点或图结构映射为连续的向量空间，便于数学运算和捕捉相似性。
  • 稠密：将稀疏的原始数据转换为稠密的向量，每个维度都包含有意义的信息。

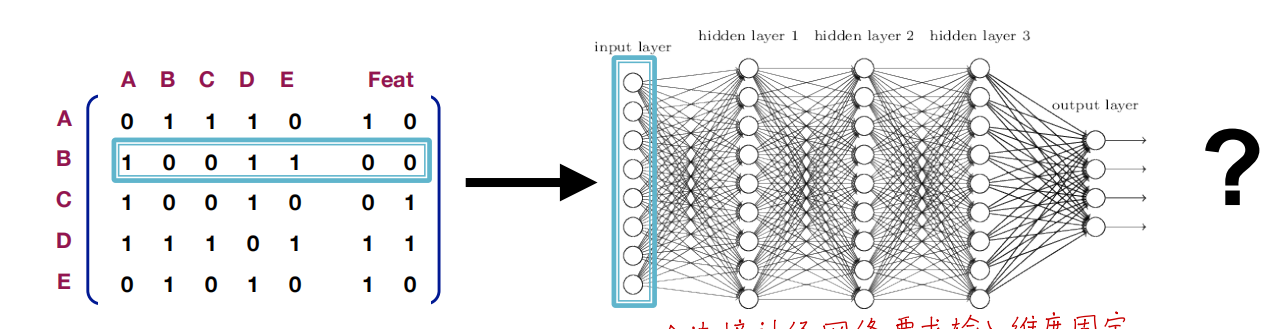
对图数据进行深度学习的“朴素做法”

把图的邻接矩阵和节点特征“直接拼接”成固定维度的输入，然后将其送入一个深度神经网络（全连接层）进行学习。

image-20250316142412685

这种做法面临重大问题，导致其并不可行：

  1. O(|V|^2) 参数量 ，参数量庞大

  2. 无法适应不同大小的图 ，需要固定输入维度

  3. 对节点顺序敏感 ，节点编号顺序一变，输入就完全变样，但其实图的拓扑并没变（仅节点编号/排列方式不同）。

       A —— B
   |     |
   D —— C

    矩阵 1（顺序 $[A,B,C,D]$）：

    
M_1 = 
\begin{pmatrix}
 0 & 1 & 0 & 1\\
 1 & 0 & 1 & 0\\
 0 & 1 & 0 & 1\\
 1 & 0 & 1 & 0
\end{pmatrix}.

    矩阵 2（顺序 $[C,A,D,B]$）：

    
M_2 =
\begin{pmatrix}
 0 & 0 & 1 & 1 \\
 0 & 0 & 1 & 1 \\
 1 & 1 & 0 & 0 \\
 1 & 1 & 0 & 0
\end{pmatrix}.

​ 两个矩阵完全不同，但它们对应的图是相同的（只不过节点的顺序改了）。

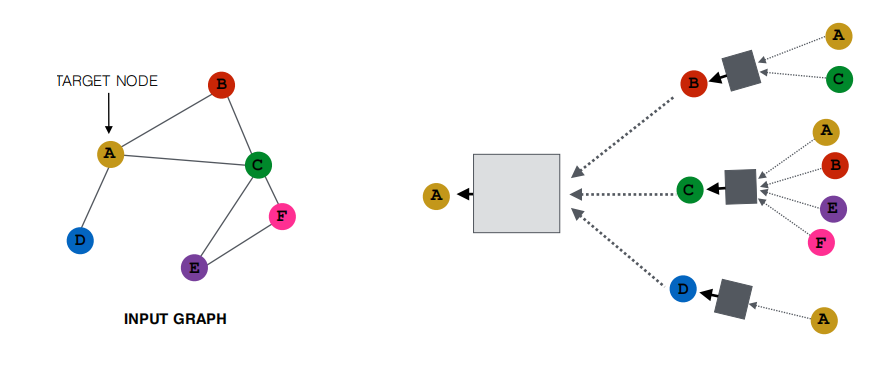
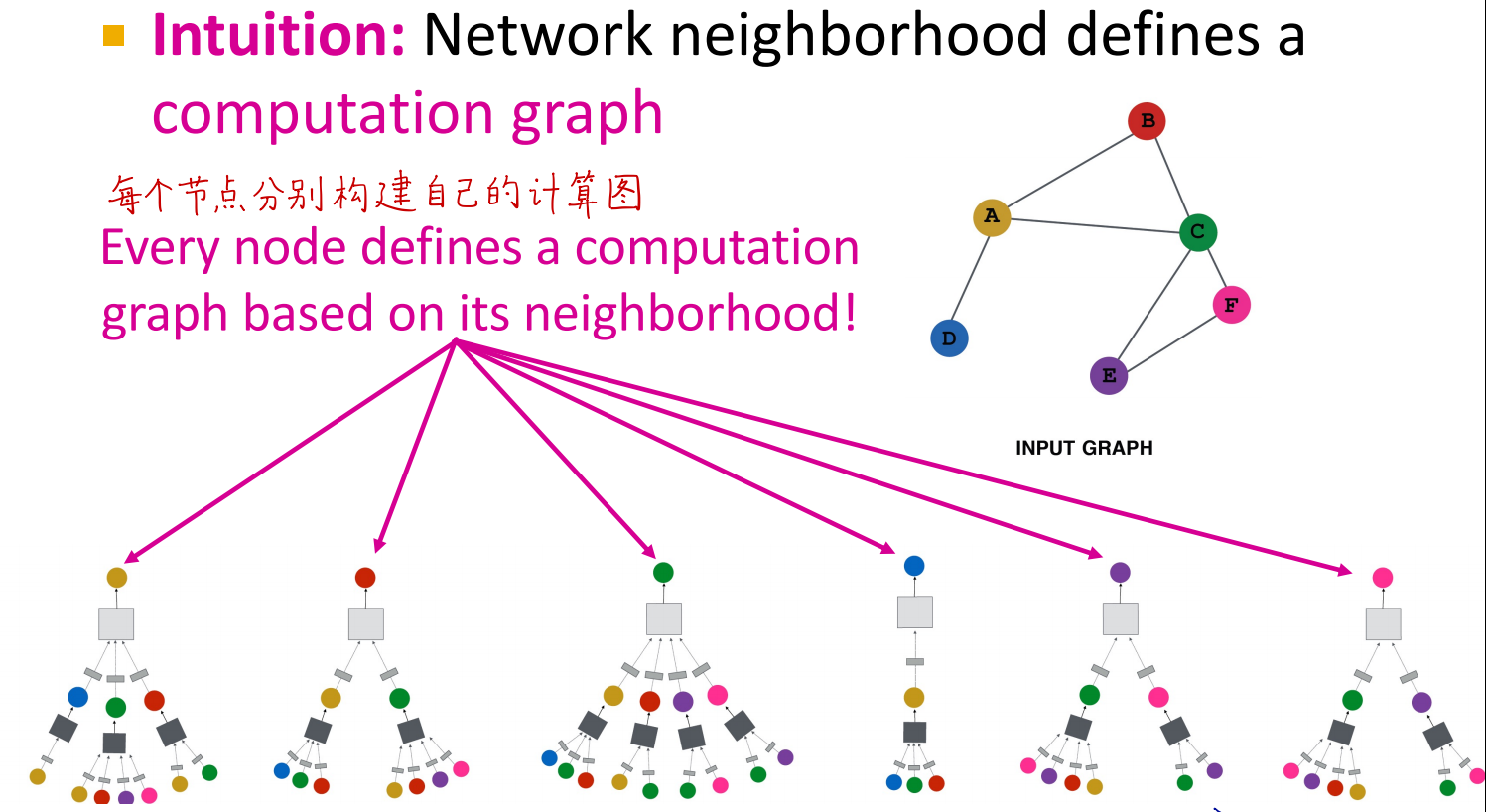
计算图

在图神经网络里，通常每个节点v 都有一个局部计算图，用来表示该节点在聚合信息时所需的所有邻居（及邻居的邻居……）的依赖关系。

直观理解

  • 以节点 v 为根；
  • 1-hop 邻居在第一层，2-hop 邻居在第二层……
  • 逐层展开直到一定深度（例如 k 层）。
  • 这样形成一棵“邻域树”或“展开图”，其中每个节点都需要从其子节点（邻居）获取特征进行聚合。

image-20250316152729679

image-20250316152836156

例子

在图神经网络中，每一层的计算通常包括以下步骤：

  1. 聚合（Aggregation）：将邻居节点的特征聚合起来（如求和、均值、最大值等）。
  2. 变换（Transformation）：将聚合后的特征通过一个神经网络（如 MLP）进行非线性变换。
      A
      |
      B
    /   \
   C     D

假设每个节点的特征是一个二维向量：

  • 节点 A 的特征：h_A = [1.0, 0.5]
  • 节点 B 的特征：h_B = [0.8, 1.2]
  • 节点 C 的特征：h_C = [0.3, 0.7]
  • 节点 D 的特征：h_D = [1.5, 0.9]

第 1 层更新：$A^{(0)} \to A^{(1)}$

  1. 节点 A 的 1-hop 邻居：只有 $B$。

  2. 聚合（示例：自+邻居取平均）：

    
z_A^{(1)} = \frac{A^{(0)} + B^{(0)}}{2} = \frac{[1.0,\,0.5] + [0.8,\,1.2]}{2} = \frac{[1.8,\,1.7]}{2} = [0.9,\,0.85].

  3. MLP 变换：用一个MLP映射 z_A^{(1)} 到 2 维输出：

    
A^{(1)} \;=\; \mathrm{MLP_1}\bigl(z_A^{(1)}\bigr).
    • （数值略，可想象 \mathrm{MLP}([0.9,0.85]) \approx [1.0,0.6] 之类。）

结果：A^{(1)} 包含了 A 的初始特征 + B 的初始特征信息。

第 2 层更新：$A^{(1)} \to A^{(2)}$

为了让 A 获得 2-hop 范围（$C, D$）的信息，需要先让 B 在第 1 层就吸收了 C, D 的特征，从而 $B^{(1)}$ 蕴含 C, D 信息。然后 A 在第 2 层再从 $B^{(1)}$ 聚合。

  1. 节点 B 在第 1 层（简要说明）

    • 邻居：\{A,C,D\}
    • 聚合：z_B^{(1)} = \frac{B^{(0)} + A^{(0)} + C^{(0)} + D^{(0)}}{4} = \frac{[0.8,\,1.2] + [1.0,\,0.5] + [0.3,\,0.7] + [1.5,\,0.9]}{4} = \frac{[3.6,\,3.3]}{4} = [0.9,\,0.825].
    • MLP 变换：$B^{(1)} = \mathrm{MLP}\bigl(z_B^{(1)}\bigr)$。
    • 此时 $B^{(1)}$ 已经包含了 C, D 的信息。

  2. 节点 A 的第 2 层聚合

    • 邻居：$B$，但此时要用 $B^{(1)}$（它已吸收 C、D）

    • 聚合：

      
z_A^{(2)} = A^{(1)} + B^{(1)}.

    • MLP 变换：

      
A^{(2)} = \mathrm{MLP_2}\bigl(z_A^{(2)}\bigr).

结果：A^{(2)} 就包含了 2-hop 范围的信息，因为 $B^{(1)}$ 中有 C, D 的贡献。

GNN 的层数就是节点聚合邻居信息的迭代次数（也是计算图的层数）。

同一层里，所有节点共享一组参数（同一个 MLP 或全连接神经网络）

矩阵运算

符号波浪号用于表示经过自环增强的矩阵。

\tilde D^{-1}\,\tilde A\,\tilde D^{-1}H

H'=\tilde D^{-1}\,\tilde A\,H

   A
   |
   B
 /   \
C     D

1.构造矩阵

含自环邻接矩阵 \tilde A=A+I


\tilde A =
\begin{bmatrix}
1 & 1 & 0 & 0\\
1 & 1 & 1 & 1\\
0 & 1 & 1 & 0\\
0 & 1 & 0 & 1
\end{bmatrix}

度矩阵 $\tilde D$（对角＝自身＋邻居数量）


\tilde D = \mathrm{diag}(2,\,4,\,2,\,2)

特征矩阵 $H$（每行为一个节点的特征向量）


H =
\begin{bmatrix}
1.0 & 0.5\\
0.8 & 1.2\\
0.3 & 0.7\\
1.5 & 0.9
\end{bmatrix}

2.计算

求和： \tilde A\,H


\tilde A H =
\begin{bmatrix}
1.8 & 1.7\\
3.6 & 3.3\\
1.1 & 1.9\\
2.3 & 2.1
\end{bmatrix}

平均： \tilde D^{-1}(\tilde A H)


\tilde D^{-1}\tilde A H =
\begin{bmatrix}
0.90 & 0.85\\
0.90 & 0.825\\
0.55 & 0.95\\
1.15 & 1.05
\end{bmatrix}

GCN

在 GCN 里，归一化（normalization）的核心目的就是 平衡不同节点在信息传播（message‑passing）中的影响力，避免「高连通度节点（high‑degree nodes）」主导了所有邻居的特征聚合。

H' = \tilde D^{-1}\,\tilde A\,\tilde D^{-1}H

  • 对节点 i 来说：

H'_i = \frac1{d_i}\sum_{j\in \mathcal N(i)}\frac1{d_j}\,H_j
  • 先用源节点 j 的度 d_j 缩小它的特征贡献，再用目标节点 i 的度 d_i 归一化总和。

GCN中实际的公式：


H^{(l+1)} = \sigma\Big(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)}\Big)

其中：

  • H^{(l)} 是第 l 层的输入特征（对第 0 层来说就是节点的初始特征），
  • W^{(l)} 是第 l 层的可训练权重矩阵，相当于一个简单的线性变换（类似于 MLP 中的全连接层），
  • \sigma(\cdot) 是非线性激活函数（例如 ReLU），
  • \tilde{A} 是包含自连接的邻接矩阵，
  • \tilde{D} 是 \tilde{A} 的度矩阵。

$\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}$的优势

1.对称归一化：\tilde D^{-\frac{1}{2}}\,\tilde A\,\tilde D^{-\frac{1}{2}} 是一个对称矩阵，这意味着信息在节点之间的传播是双向一致的。这种对称性特别适合无向图，因为无向图的邻接矩阵 \tilde A 本身就是对称的。

2.适度抑制高连通度节点：对称平方根归一化通过 \tilde D^{-\frac{1}{2}} 对源节点和目标节点同时进行归一化，能够适度抑制高连通度节点的特征贡献，而不会过度削弱其影响力。

3.谱半径控制：对称平方根归一化后的传播矩阵 \tilde D^{-\frac{1}{2}}\,\tilde A\,\tilde D^{-\frac{1}{2}} 的谱半径（最大特征值）被控制在 [0, 1] 范围内，这有助于保证模型的数值稳定性。

4.归一化拉普拉斯矩阵：对称平方根归一化的传播矩阵 \tilde D^{-\frac{1}{2}}\,\tilde A\,\tilde D^{-\frac{1}{2}} 与归一化拉普拉斯矩阵 L = I - \tilde D^{-\frac{1}{2}}\,\tilde A\,\tilde D^{-\frac{1}{2}} 有直接联系。归一化拉普拉斯矩阵在图信号处理中具有重要的理论意义，能够更好地描述图的频谱特性。

GraphSAGE优化


h_v^{(k+1)} = \sigma \Big(
   \mathbf{W}_{\text{self}}^{(k)} \cdot h_v^{(k)} 
   \;+\; 
   \mathbf{W}_{\text{neigh}}^{(k)} \cdot \mathrm{MEAN}_{u\in N(v)}\bigl(h_u^{(k)}\bigr)
\Big),

GAT

图注意力网络（GAT）中最核心的运算：图注意力层。它的基本思想是：

  1. 线性变换：先对每个节点的特征 \mathbf{h}_i 乘上一个可学习的权重矩阵 $W$，得到变换后的特征 $W \mathbf{h}_i$。
  2. 自注意力机制：通过一个可学习的函数 $a$，对节点 i 和其邻居节点 j 的特征进行计算，得到注意力系数 $e_{ij}$。这里会对邻居进行遮蔽（masked attention），即只计算图中有边连接的节点对。
  3. 归一化：将注意力系数 e_{ij} 通过 softmax 进行归一化，得到 $\alpha_{ij}$，表示节点 j 对节点 i 的重要性权重。
  4. 聚合：最后利用注意力系数加权邻居节点的特征向量，并经过激活函数得到新的节点表示 $\mathbf{h}_i'$。
  5. 多头注意力：为增强表示能力，可并行地执行多个独立的注意力头（multi-head attention），再将它们的结果进行拼接（或在最后一层进行平均），从而得到最终的节点表示。

输入：

  1. 节点特征矩阵（Node Features）

    • 形状：[num_nodes, num_features]
    • 每个节点的初始特征向量，例如社交网络中用户的属性或分子图中原子的特征。

  2. 图的边结构（Edge Index）

    • 形状：**[2, num_edges]（稀疏邻接表格式）**或稠密邻接矩阵 [num_nodes, num_nodes]（最好是将邻接矩阵转为邻接表）

    • 定义图中节点的连接关系（有向/无向边）。

  3. 预训练的GAT模型参数

    • 包括注意力层的权重矩阵、注意力机制参数等（通过model.load_state_dict()加载）

线性变换（特征投影）

  • 目的：将原始特征映射到更高维/更有表达力的空间。

  • 操作：对每个节点的特征向量 \mathbf{h}_i 左乘可学习权重矩阵 $W$（维度为 $d' \times d$，d 是输入特征维度，d' 是输出维度）：

    
\mathbf{z}_i = W \mathbf{h}_i, \quad \mathbf{z}_j = W \mathbf{h}_j

自注意力系数计算（关键步骤）

  • 目标：计算节点 i 和邻居 j 之间的未归一化注意力得分 $e_{ij}$。

  • 实现方式：

    • 步骤1：将两个节点的投影特征 \mathbf{z}_i 和 \mathbf{z}_j 拼接（$|$），得到一个联合表示。

    • 步骤2：通过一个可学习的参数向量 $\mathbf{a}$（维度 $2d'$）和激活函数（如LeakyReLU）计算得分：

      
e_{ij} = \text{LeakyReLU}\Bigl(\mathbf{a}^\top [\mathbf{z}_i \| \mathbf{z}_j]\Bigr)
      • 直观理解：\mathbf{a} 像一个"问题"，询问两个节点的联合特征有多匹配。
      • 公式拆分：
        1. 拼接：$[\mathbf{z}_i | \mathbf{z}_j]$（长度 $2d'$）
        2. 点积：$\mathbf{a}^\top [\mathbf{z}_i | \mathbf{z}_j]$（标量）
        3. 非线性激活：LeakyReLU（引入稀疏性，避免负值被完全抑制）

归一化注意力权重

  • 目的：让注意力系数在邻居间具有可比性（总和为1）。

  • 方法：对 e_{ij} 应用 softmax，仅对节点 i 的邻居 \mathcal{N}_i 归一化：

    
\alpha_{ij} = \text{softmax}_j(e_{ij}) = \frac{\exp(e_{ij})}{\sum_{k \in \mathcal{N}_i} \exp(e_{ik})}
    • 关键点：分母只包含节点 i 的直接邻居（包括自己，如果图含自环）。

注意力系数计算示例（带数值模拟）

假设：

  • 输入特征 \mathbf{h}_i = [1.0, 2.0], $\mathbf{h}_j = [0.5, 1.5]$（维度 $d=2$）
  • 权重矩阵 $W = \begin{bmatrix}0.1 & 0.2 \ 0.3 & 0.4\end{bmatrix}$（$d'=2$）
  • 参数向量 $\mathbf{a} = [0.5, -0.1, 0.3, 0.2]$（长度 $2d'=4$）

计算步骤：

  1. 线性变换：

    
\mathbf{z}_i = W \mathbf{h}_i = [0.1 \times 1.0 + 0.2 \times 2.0,\ 0.3 \times 1.0 + 0.4 \times 2.0] = [0.5, 1.1]

    
\mathbf{z}_j = W \mathbf{h}_j = [0.1 \times 0.5 + 0.2 \times 1.5,\ 0.3 \times 0.5 + 0.4 \times 1.5] = [0.35, 0.75]

  2. 拼接特征：

    
[\mathbf{z}_i \| \mathbf{z}_j] = [0.5, 1.1, 0.35, 0.75]\\
[\mathbf{z}_i \| \mathbf{z}_i] = [0.5, 1.1, 0.5, 1.1]

  3. 计算未归一化得分：

    
e_{ij} = \text{LeakyReLU}(0.5 \times 0.5 + (-0.1) \times 1.1 + 0.3 \times 0.35 + 0.2 \times 0.75) = \text{LeakyReLU}(0.25 - 0.11 + 0.105 + 0.15) = \text{LeakyReLU}(0.395) = 0.395

    
e_{ii} = \text{LeakyReLU}(0.5 \times 0.5 + (-0.1) \times 1.1 + 0.3 \times 0.5 + 0.2 \times 1.1)=0.51

    （假设LeakyReLU斜率为0.2，正输入不变）

  4. 归一化（假设邻居只有 j 和自身 $i$）：

    
\alpha_{ij} = \frac{\exp(0.395)}{\exp(0.395) + \exp(0.51)}\approx 0.529

特征聚合

单头注意力聚合（得到新的节点特征）


\mathbf{h}_i' = \sigma\Bigl(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \,W \mathbf{h}_j\Bigr)=\sigma\left(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \mathbf{z}_j\right)

对i 的邻居节点加权求和，再经过非线性激活函数得到新的特征表示

多头注意力(隐藏层时拼接)

每个头都有自己的一组可学习参数，并独立计算注意力系数和输出特征。以捕捉邻居节点的多种不同关系或特征。

如果有 K 个独立的注意力头，每个头输出 $\mathbf{h}_i'^{(k)}$，则拼接后的输出为：


\begin{align*}
\mathbf{h}_i' = \Bigg\Vert_{\substack{k=1 \\ ~}}^{K} \mathbf{h}_i^{(k)}
\end{align*}

其中，\big\Vert 表示向量拼接操作，$\alpha_{ij}^{(k)}$、W^{(k)} 分别为第 k 个注意力头对应的注意力系数和线性变换。

例假如：


\mathbf{h}_i'^{(1)} = \sigma\left(\begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix}\right)
= \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix}. \\
\mathbf{h}_i'^{(2)} = \sigma\left(\begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}\right)
= \begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}.

将两个头的输出在特征维度上进行拼接，得到最终节点 i 的新特征表示：


\mathbf{h}_i' = \mathbf{h}_i'^{(1)} \,\Vert\, \mathbf{h}_i'^{(2)}
= \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} \,\Vert\, \begin{bmatrix} 0.6 \\ 1.4 \end{bmatrix}
= \begin{bmatrix} 0.6 \\ 0.4 \\ 0.6 \\ 1.4 \end{bmatrix}.

意义：不同注意力头可以学习到节点之间不同类型的依赖关系。例如：

  • 一个头可能关注局部邻居（如一阶邻居的拓扑结构），
  • 另一个头可能关注全局特征相似性（如节点特征的余弦相似性）。

多头注意力（输出层时平均）

在最终的输出层（例如分类层）通常会将多个头的结果做平均，而不是拼接：


\begin{align*}
\mathbf{h}_i' = \sigma\left(\frac{1}{K}\sum_{k=1}^K \mathbf{h}_i^{(k)}\right)
\end{align*}

多头注意力比喻：盲人摸象 + 团队合作

场景：

  • 大象 = 图中的目标节点及其邻居（待分析的复杂结构）
  • 盲人 = 多个注意力头（每个头独立"观察"）
  • 团队指挥 = 损失函数（指导所有盲人协作）

1. 初始摸象（前向传播）

  • 盲人A（头1）：

    • 摸到腿（关注局部结构邻居），心想："柱子！这动物像房子。"（生成表示 $\mathbf{h}_i^{(1)}$）
    • 初始偏好：腿的粗细、纹理（权重 W^{(1)} 和 \mathbf{a}^{(1)} 的初始化倾向）

  • 盲人B（头2）：

    • 摸到鼻子（关注特征相似的邻居），心想："软管！这动物能喷水。"（生成表示 $\mathbf{h}_i^{(2)}$）
    • 初始偏好：鼻子的长度、灵活性（权重 W^{(2)} 和 \mathbf{a}^{(2)} 不同）

  • 盲人C（头3）：

    • 摸到尾巴（关注远距离邻居），心想："绳子！这动物有附件。"（生成表示 $\mathbf{h}_i^{(3)}$）

2. 团队汇报（多头聚合）

  • 综合报告：
    • 将三人的描述拼接："柱子+软管+绳子"（$\mathbf{h}_i' = \text{concat}(\mathbf{h}_i^{(1)}, \mathbf{h}_i^{(2)}, \mathbf{h}_i^{(3)})$）
    • 指挥者（分类器）猜测："这可能是大象。"（预测结果 $\hat{y}_i$）

3. 指挥者反馈（损失函数）

  • 真实答案：是大象（标签 $y_i$）
  • 损失计算：
    • 当前综合报告遗漏了"大耳朵"（交叉熵损失 \mathcal{L} 较高）
    • 指挥者说："接近答案，但还缺关键特征！"（反向传播梯度）

4. 盲人调整（梯度更新）

  • 盲人A（头1）：

    • 听到反馈："需要更多特征，但你的柱子描述还行。"
    • 调整：更精确测量腿的直径和硬度（更新 $W^{(1)}$），而非改摸鼻子
    • 结果：下次报告"粗柱子上有横向褶皱"（更接近象腿的真实特征）

  • 盲人B（头2）：

    • 听到反馈："软管描述不够独特。"
    • 调整：更仔细感受鼻子的褶皱和肌肉运动（更新 $W^{(2)}$）
    • 结果：下次报告"可弯曲的软管，表面有环形纹路"

  • 盲人C（头3）：

    • 听到反馈："绳子太模糊。"
    • 调整：注意尾巴的末端毛发（更新 $W^{(3)}$）
    • 结果：下次报告"短绳末端有硬毛刷"

5. 最终协作

  • 新一轮综合报告："褶皱粗柱 + 环形软管 + 带毛刷短绳" → 指挥者确认："是大象！"（损失 \mathcal{L} 降低）

直推式学习与归纳式学习

直推式学习（Transductive Learning） 模型直接在固定的训练图上学习节点的表示或标签，结果只能应用于这张图中的节点，无法直接推广到新的、未见过的节点或图。

例如：DeepWalk ，它通过对固定图的随机游走生成节点序列来学习节点嵌入，因此只能得到训练图中已有节点的表示，一旦遇到新节点，需要重新训练或进行特殊处理。

注意：GCN是直推式的，因为它依赖于整个图的归一化邻接矩阵进行卷积操作，需要在固定图上训练。

归纳式学习（Inductive Learning） 模型学习的是一个映射函数或规则，可以将这种规则推广到未见过的新节点或新图上。这种方法能够处理动态变化的图结构或新的数据。

例如：

图神经网络的变体（GAT）都是归纳式的，因为它们在聚合邻居信息时学习一个共享的函数，该函数能够应用于任意新节点。

  • 局部计算：GAT 的注意力机制仅在每个节点的局部邻域内计算，不依赖于全局图结构。
  • 参数共享：模型中每一层的参数（如 W 和注意力参数 $\mathbf{a}$）是共享的，可以直接应用于新的、未见过的图。

泛化到新节点：在许多推荐系统中，如果有新用户加入（新节点），我们需要给他们做个性化推荐，这就要求系统能够在不重新训练整个模型的情况下，为新用户生成表示（Embedding），并且完成推荐预测。

泛化到新图： 分子图预测。我们会用一批训练分子（每个分子是一张图）来训练一个 GNN 模型，让它学会如何根据图结构与原子特征来预测分子的某些性质（如毒性、溶解度、活性等）。训练完成后，让它在新的分子上做预测。

总结：直推式要求图的邻接矩阵不能变化，归纳式要求现有的邻接关系尽量不变化，支持少量节点新加入，直接复用已有W和a聚合特征。

GNN的优点：

参数共享

  • 浅层嵌入(如Deepwalk)为每个节点单独学习一个向量，参数量随节点数线性增长。
  • GNN 使用统一的消息传递/聚合函数，所有节点共享同一套模型参数，大幅减少参数量。

归纳式学习

  • 浅层方法通常无法直接处理训练时未见过的新节点。
  • GNN 能通过邻居特征和结构来生成新节点的表示，实现对新节点/新图的泛化。

利用节点特征

  • 浅层方法多半只基于连接关系（图结构）。
  • GNN 可以直接整合节点的属性（文本、图像特征等），生成更具语义信息的嵌入。

更强的表达能力

  • GNN 通过多层聚合邻居信息，可学习到更丰富的高阶结构和特征交互，往往在多种任务上表现更优。