486 lines
16 KiB
Markdown
486 lines
16 KiB
Markdown
# 高飞论文
|
||
|
||
## 证明特征值序列为平稳的时间序列
|
||
|
||
### 问题设定
|
||
|
||
- **研究对象**
|
||
设 $\{\lambda_1(A)_t\}_{t\in\mathbb Z}$ 是随时间变化的随机对称矩阵 $A_t$ 的最大特征值序列(如动态网络的邻接矩阵)。
|
||
- **目标**
|
||
证明 $\{\lambda_1(A)_t\}$ 是 **二阶(弱)平稳**的时间序列,即
|
||
1. $E[\lambda_1(A)_t]=\mu_1$(与 $t$ 无关);
|
||
2. $\operatorname{Var}[\lambda_1(A)_t]=\sigma_1^2<\infty$(与 $t$ 无关);
|
||
3. $\operatorname{Cov}(\lambda_1(A)_t,\lambda_1(A)_{t-k})=\gamma(k)$ 只依赖滞后 $k$。
|
||
|
||
|
||
|
||
### 关键假设
|
||
|
||
- **矩阵统计特性(引理 1)**
|
||
|
||
- $A_t$ 为 $N\times N$ 实对称随机矩阵;元素 $\{a_{ij}\}_{i\le j}$ 相互独立且有界:$|a_{ij}|\le K$。
|
||
|
||
- 非对角元素:$E[a_{ij}]=\mu>0,\ \operatorname{Var}(a_{ij})=\sigma^2$;对角元素:$E[a_{ii}]=v$。
|
||
|
||
- $N$ 足够大时
|
||
$$
|
||
E[\lambda_1(A_t)]\approx(N-1)\mu+v+\tfrac{\sigma^2}{\mu}\equiv\mu_1,\qquad
|
||
\operatorname{Var}[\lambda_1(A_t)]\approx2\sigma^2\equiv\sigma_1^2 .
|
||
$$
|
||
|
||
说明:
|
||
|
||
- **$\sigma^2$**
|
||
这是随机矩阵 $A_t$ 的非对角线元素 $a_{ij}$ ($i \neq j$) 的方差,即
|
||
$$
|
||
\text{Var}(a_{ij}) = \sigma^2.
|
||
$$
|
||
根据引理1的假设,所有非对角线元素独立同分布,均值为 $\mu$,方差为 $\sigma^2$。
|
||
|
||
- **$\sigma_1^2$**
|
||
这是最大特征值 $\lambda_1(A_t)$ 的方差,即
|
||
$$
|
||
\text{Var}[\lambda_1(A_t)] \equiv \sigma_1^2.
|
||
$$
|
||
当 $N$ 足够大时,$\sigma_1^2$ 近似为 $2\sigma^2$。
|
||
|
||
- **时间序列模型**
|
||
对**去中心化序列**
|
||
$$
|
||
\tilde z_t:=\lambda_1(A)_t-\mu_1
|
||
$$
|
||
假设其服从 AR(1)
|
||
$$
|
||
\tilde z_t=\rho\,\tilde z_{t-1}+\varepsilon_t,\qquad
|
||
\varepsilon_t\stackrel{\text{i.i.d.}}{\sim}\text{WN}(0,\sigma_\varepsilon^{2}),\ \ |\rho|<1,
|
||
$$
|
||
且 $\varepsilon_t$ 与历史 $\{\tilde z_{s}\}_{s<t}$ 独立。
|
||
|
||
|
||
|
||
### 证明主特征值序列平稳
|
||
|
||
#### **(1) 均值恒定性的推导**
|
||
|
||
- 去中心化后 $E[\tilde z_t]=0$。因此
|
||
$$
|
||
E[\lambda_1(A)_t]=E[\tilde z_t]+\mu_1=\mu_1,
|
||
$$
|
||
与 $t$ 无关,满足第一条。
|
||
|
||
#### (2) 方差恒定
|
||
|
||
AR(1)模型定义为:
|
||
$$
|
||
z_t = \rho z_{t-1} + \varepsilon_t
|
||
$$
|
||
|
||
$$
|
||
\begin{aligned}
|
||
z_t &= \varepsilon_t + \rho z_{t-1} \\
|
||
&= \varepsilon_t + \rho (\varepsilon_{t-1} + \rho z_{t-2}) \\
|
||
&= \varepsilon_t + \rho \varepsilon_{t-1} + \rho^2 \varepsilon_{t-2} + \cdots \\
|
||
&= \sum_{j=0}^\infty \rho^j \varepsilon_{t-j}
|
||
\end{aligned}
|
||
$$
|
||
|
||
$$
|
||
\text{Var}(z_t) = \text{Var}\left( \sum_{j=0}^\infty \rho^j \varepsilon_{t-j} \right)= \sum_{j=0}^\infty \rho^{2j} \text{Var}(\varepsilon_{t-j})
|
||
$$
|
||
|
||
由于$\text{Var}(\varepsilon_{t-j}) = \sigma_\varepsilon^2$ 对所有 $j$ 成立,
|
||
$$
|
||
= \sigma_\varepsilon^2 \sum_{j=0}^\infty \rho^{2j}=\frac{\sigma_\varepsilon^2}{1-\rho^2}
|
||
$$
|
||
|
||
- **$|\rho| < 1$** 是保证级数收敛和方差有限的充要条件。
|
||
|
||
|
||
|
||
根据引理1,$\text{Var}[\lambda_1(A_t)] \approx 2\sigma^2 = \sigma_1^2$。为使模型与理论一致,可设:
|
||
$$
|
||
\sigma_\varepsilon^2 = (1 - \rho^2) \cdot 2\sigma^2
|
||
$$
|
||
|
||
此时:
|
||
|
||
$$
|
||
\text{Var}[\tilde{z}_t] = 2\sigma^2 = \sigma_1^2
|
||
$$
|
||
|
||
|
||
|
||
|
||
#### **(3) 协方差仅依赖滞后 $k$**
|
||
|
||
对 $k\ge0$,
|
||
$$
|
||
\gamma(k):=\operatorname{Cov}(\tilde z_t,\tilde z_{t-k})
|
||
=\rho^{k}\sigma_{\tilde z}^{2},
|
||
$$
|
||
仅含 $k$ 而与 $t$ 无关;于是
|
||
$$
|
||
\operatorname{Cov}(\lambda_1(A)_t,\lambda_1(A)_{t-k})=\gamma(k),
|
||
$$
|
||
满足第三条。
|
||
|
||
|
||
|
||
#### (4) 平稳性的核心条件
|
||
|
||
1. **|ρ| < 1 是关键条件**
|
||
- 直观上:$\rho$ 越小,当前特征值对过去的依赖越弱;
|
||
- $\rho=\pm1$ 会让方差发散,不可能稳态。
|
||
2. **噪声独立性**:$\varepsilon_t$ 为白噪声,确保新信息与历史无关。
|
||
|
||
|
||
|
||
### 证明剩余特征值平稳:
|
||
|
||
#### 1. 收缩操作(Deflation)的严格定义
|
||
|
||
设 $A_t$ 的谱分解为:
|
||
$$
|
||
A_t = \sum_{i=1}^N \lambda_i u_i u_i^\top,
|
||
$$
|
||
其中 $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_N$,且 $\{u_i\}$ 是标准正交基。
|
||
|
||
- **第一次收缩**:
|
||
定义剩余矩阵 $A_{t,2} = A_t - \lambda_1 u_1 u_1^\top$,其性质为:
|
||
|
||
- 特征值:$\lambda_2, \lambda_3, \dots, \lambda_N$(即移除 $\lambda_1$ 后剩余特征值不变)。
|
||
- 特征向量:$u_2, \dots, u_N$ 保持不变(因 $u_1$ 与其他特征向量正交)。
|
||
|
||
- **第 $k$ 次收缩**:
|
||
递归定义:
|
||
$$
|
||
A_{t,k+1} = A_{t,k} - \lambda_k u_k u_k^\top,
|
||
$$
|
||
剩余矩阵 $A_{t,k+1}$ 的特征值为 $\lambda_{k+1}, \dots, \lambda_N$。
|
||
|
||
每次收缩移除当前主成分,剩余矩阵的特征值是原始矩阵中未被移除的部分。
|
||
|
||
---
|
||
|
||
#### 2. 剩余特征值的统计特性
|
||
|
||
**目标**:证明 $\{\lambda_k(A_t)\}_{t \in \mathbb{Z}}$ 对 $k \geq 2$ 也是弱平稳的。
|
||
|
||
##### **(1) 均值恒定性**
|
||
|
||
- **剩余矩阵的期望**:
|
||
由线性性:
|
||
$$
|
||
E[A_{t,k+1}] = E[A_t] - \sum_{i=1}^k E[\lambda_i u_i u_i^\top].
|
||
$$
|
||
若 $A_t$ 的元素分布时不变,且 $\lambda_i$ 和 $u_i$ 的期望稳定(由主特征值的平稳性保证),则 $E[A_{t,k+1}]$ 与 $t$ 无关。
|
||
|
||
- **特征值期望**:
|
||
对剩余矩阵 $A_{t,k+1}$,其主特征值 $\lambda_{k+1}(A_t)$ 的期望近似为:
|
||
$$
|
||
E[\lambda_{k+1}(A_t)] \approx (N-k-1)\mu + v + \frac{\sigma^2}{\mu} \equiv \mu_{k+1},
|
||
$$
|
||
其中 $(N-k-1)\mu$ 是剩余非对角元素的贡献(假设每次收缩后非对角元素统计特性不变)。
|
||
|
||
##### **(2) 方差恒定性**
|
||
|
||
- **剩余矩阵的方差**:
|
||
收缩操作通过正交投影移除 $\lambda_k u_k u_k^\top$,因此剩余矩阵 $A_{t,k+1}$ 的元素方差仍为 $\sigma^2$(对角元素可能需调整)。
|
||
由引理1的推广:
|
||
$$
|
||
\text{Var}[\lambda_{k+1}(A_t)] \approx 2\sigma^2 \equiv \sigma_{k+1}^2.
|
||
$$
|
||
|
||
- **动态模型**:
|
||
假设去中心化序列 $\tilde{z}_{k+1,t} = \lambda_{k+1}(A_t) - \mu_{k+1}$ 服从AR(1):
|
||
$$
|
||
\tilde{z}_{k+1,t} = \rho_{k+1} \tilde{z}_{k+1,t-1} + \varepsilon_{k+1,t}, \quad |\rho_{k+1}| < 1,
|
||
$$
|
||
稳态方差为:
|
||
$$
|
||
\sigma_{\tilde{z}_{k+1}}^2 = \frac{\sigma_{\varepsilon_{k+1}}^2}{1-\rho_{k+1}^2} = \sigma_{k+1}^2.
|
||
$$
|
||
|
||
##### **(3) 协方差仅依赖滞后 $m$**
|
||
|
||
- 协方差函数:
|
||
$$
|
||
\gamma_{k+1}(m) = \text{Cov}(\tilde{z}_{k+1,t}, \tilde{z}_{k+1,t-m}) = \rho_{k+1}^{|m|} \sigma_{\tilde{z}_{k+1}}^2.
|
||
$$
|
||
仅依赖 $m$,与 $t$ 无关。
|
||
|
||
---
|
||
|
||
#### **3. 递推证明的完整性**
|
||
|
||
1. **归纳基础**:
|
||
$k=1$ 时(主特征值),平稳性已证。
|
||
|
||
2. **归纳假设**:
|
||
假设 $\lambda_k(A_t)$ 的平稳性成立,即:
|
||
- $E[\lambda_k(A_t)] = \mu_k$(常数),
|
||
- $\text{Var}[\lambda_k(A_t)] = \sigma_k^2$(有限),
|
||
- $\text{Cov}(\lambda_k(A_t), \lambda_k(A_{t-m})) = \gamma_k(m)$。
|
||
|
||
3. **归纳步骤**:
|
||
- 通过收缩操作,$\lambda_{k+1}(A_t)$ 成为 $A_{t,k+1}$ 的主特征值。
|
||
- 若 $A_{t,k+1}$ 满足与 $A_t$ 相同的统计假设(独立性、有界性、时不变性),则 $\lambda_{k+1}(A_t)$ 的平稳性可类比主特征值的证明。
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
## 网络重构分析
|
||
|
||
### **0/1矩阵**
|
||
|
||
这里以n个特征值特征向量重构为例!
|
||
|
||
假设网络中有 $n$ 个节点,则矩阵 $A(G)$ 的维度为 $n \times n$,预测得到特征值和特征向量后,可以根据矩阵谱分解理论进行逆向重构网络邻接矩阵,表示如下:
|
||
|
||
$$
|
||
A(G) = \sum_{i=1}^n \hat{\lambda}_i \hat{x}_i \hat{x}_i^T
|
||
$$
|
||
|
||
其中 $\hat{\lambda}_i$ 和 $\hat{x}_i$ 分别为通过预测得到矩阵 $A(G)$ 的第 $i$ 个特征值和对应特征向量。 然而预测值和真实值之间存在误差,直接进行矩阵重构会使得重构误差较大。 对于这个问题,文献提出一种 0/1 矩阵近似恢复算法。
|
||
$$
|
||
a_{ij} =
|
||
\begin{cases}
|
||
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
|
||
0, & \text{else}
|
||
\end{cases}
|
||
$$
|
||
只要我们的估计值与真实值之间差距**小于 0.5**,就能保证阈值处理以后准确地恢复原边信息。
|
||
|
||
|
||
|
||
文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律
|
||
|
||
真实矩阵 $A(G)$ 与预测矩阵 $\hat{A}(G) $ 之间的差为
|
||
$$
|
||
A(G) - \hat{A}(G) = \sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
|
||
$$
|
||
对于任意元素 $(i, j)$ 上有
|
||
$$
|
||
\left| \sum_{m=1}^n \Delta \lambda_m (\hat{x}_m \hat{x}_m^T)_{ij} \right| = |a_{ij} - \hat{a}_{ij}| < \frac{1}{2}
|
||
$$
|
||
|
||
于一个归一化的特征向量 $\hat{x}_m$,其外积矩阵 $\hat{x}_m \hat{x}_m^T$ 的元素理论上满足
|
||
$$
|
||
|(\hat{x}_m \hat{x}_m^T)_{ij}| \leq 1.
|
||
$$
|
||
经过分析推导可以得出发生特征扰动时,网络精准重构条件为:
|
||
$$
|
||
\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}
|
||
$$
|
||
|
||
$$
|
||
\Delta {\lambda} < \frac{1}{2n}
|
||
$$
|
||
|
||
0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比,网络中节点数量越多,实现精准重构的要求也就越高。
|
||
|
||
|
||
|
||
如果在**高层次**(特征值滤波)的误差累积超过了一定阈值,就有可能在**低层次**(邻接矩阵元素)中出现翻转。公式推导了只要谱参数的误差之和**不超过** 0.5,就可以保证0-1矩阵的精确重构。
|
||
|
||
|
||
|
||
### **非0/1矩阵**
|
||
|
||
- 原始(真)加权邻接矩阵:
|
||
$$
|
||
A = \sum_{m=1}^n \lambda_m\,x_m x_m^T,
|
||
\quad \lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n,\;
|
||
x_m^T x_k=\delta_{mk}.
|
||
$$
|
||
|
||
- 估计得到的矩阵及谱分解:
|
||
$$
|
||
\widetilde A = \sum_{m=1}^n \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||
\quad \widetilde\lambda_1\ge\cdots\ge\widetilde\lambda_n,\;
|
||
\widetilde x_m^T\widetilde x_k=\delta_{mk}.
|
||
$$
|
||
|
||
- 最终只取前 $r$ 项重构 :
|
||
$$
|
||
A_r \;=\;\sum_{m=1}^r \widetilde\lambda_m\,\widetilde x_m\widetilde x_m^T,
|
||
$$
|
||
|
||
|
||
#### **全局误差度量**
|
||
|
||
对估计矩阵 $\widetilde{A}$ 的所有元素 $\{\tilde{a}_{ij}\}$ 进行 $K$-means 聚类,得到中心 $\{c_k\}_{k=1}^K$。
|
||
|
||
- **簇内平均偏差**:
|
||
$$
|
||
\text{mean}_k = \frac{1}{|\mathcal{S}_k|} \sum_{(i,j)\in\mathcal{S}_k} |\tilde{a}_{ij} - c_k|
|
||
$$
|
||
|
||
- **全局允许误差**:
|
||
$$
|
||
\delta_{\max} = \frac{1}{K} \sum_{k=1}^K \text{mean}_k
|
||
$$
|
||
|
||
#### 带权重构需控制两类误差:
|
||
|
||
1. **谱分解截断误差**$\epsilon$:
|
||
$$
|
||
\epsilon
|
||
= \bigl\|\widetilde A - A_r\bigr\|_F
|
||
= \Bigl\|\sum_{m=r+1}^n \widetilde\lambda_m\,\widetilde x_m \widetilde x_m^T\Bigr\|_F.
|
||
$$
|
||
|
||
---
|
||
|
||
2. **滤波误差**$\eta$:
|
||
|
||
**来源**:滤波器在谱域对真实特征值/向量的估计偏差,包括
|
||
|
||
- 特征值偏差 $\Delta\lambda_m=\lambda_m-\widetilde\lambda_m$
|
||
- 特征向量:矩阵扰动得来,不知道该不该算
|
||
|
||
$$
|
||
A - \widetilde A=\sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.
|
||
$$
|
||
|
||
$$
|
||
\eta \approx \Bigl\|\sum_{m=1}^n \Delta\lambda_m\,\widetilde x_m\widetilde x_m^T\Bigr\|_F
|
||
$$
|
||
|
||
#### **最终约束条件**:
|
||
|
||
$$
|
||
\boxed{
|
||
\underbrace{\eta}_{\text{滤波误差}}
|
||
\;+\;
|
||
\underbrace{\epsilon}_{\text{谱分解截断误差}}
|
||
\;\le\;
|
||
\underbrace{\delta_{\max}}_{\text{聚类量化容限}}
|
||
}
|
||
$$
|
||
|
||
|
||
|
||
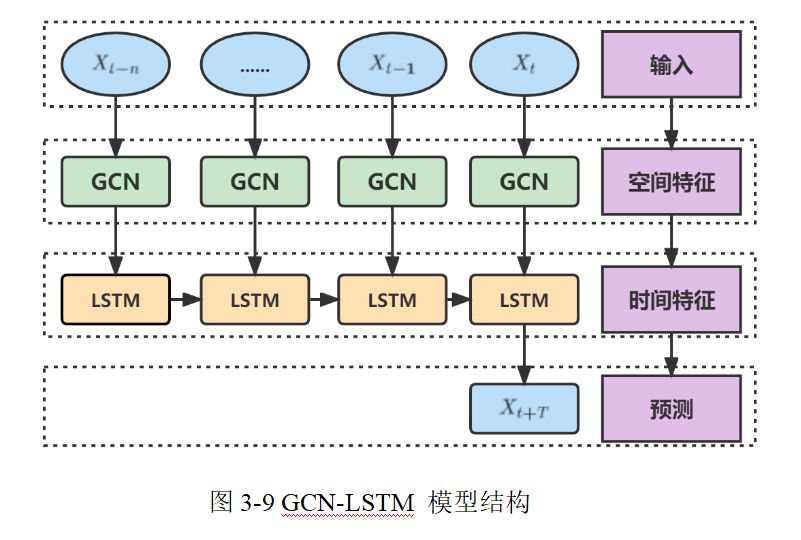
## 基于时空特征的节点位置预测
|
||
|
||
在本模型中,整个预测流程分为两大模块:
|
||
|
||
- **GCN 模块:主要用于从当前网络拓扑中提取每个节点的**空间表示**。这里的输入主要包括:
|
||
- **邻接矩阵 $A$**:反映网络中节点之间的连通关系,维度为 $N \times N$,其中 $N$ 表示节点数。(可通过第二章网络重构的方式获取)
|
||
- **特征矩阵 $H^{(0)}$**:一般是原始节点的属性信息,如历史位置数据,其维度为 $N \times d$,其中 $d$ 是初始特征维度。
|
||
|
||
- **LSTM 模块**:用于捕捉节点随时间变化的动态信息,对每个节点的历史运动轨迹进行序列建模,并预测未来时刻的坐标。
|
||
其输入通常是经过 GCN 模块处理后,每个节点在一段时间内获得的时空融合特征序列,维度一般为 $N \times T \times d'$,其中 $T$ 表示时间步数,$d'$ 是经过 GCN 后的特征维度。
|
||
|
||
|
||
|
||
### GCN 模块
|
||
|
||
#### 输入
|
||
|
||
- **邻接矩阵 $A$**:维度 $N \times N$。在实际操作中,通常先加上自环形成
|
||
$$
|
||
\hat{A} = A + I.
|
||
$$
|
||
|
||
- **特征矩阵 $H^{(0)}$**:维度 $N \times d$,每一行对应一个节点的初始特征(例如历史采样的位置信息或其他描述)。
|
||
|
||
#### 图卷积操作
|
||
|
||
常用的图卷积计算公式为:
|
||
$$
|
||
H^{(l+1)} = \sigma \Bigl(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} H^{(l)} W^{(l)} \Bigr)
|
||
$$
|
||
其中:
|
||
|
||
- $\tilde{A} = A + I$ 为加上自环后的邻接矩阵,
|
||
- $\tilde{D}$ 为 $\tilde{A}$ 的度矩阵,定义为 $\tilde{D}_{ii} = \sum_{j}\tilde{A}_{ij}$;
|
||
- $H^{(l)}$ 表示第 $l$ 层的节点特征,初始时 $H^{(0)}$ 就是输入特征矩阵;
|
||
- $W^{(l)}$ 是第 $l$ 层的权重矩阵,其维度通常为 $d_l \times d_{l+1}$(例如从 $d$ 到 $d'$);
|
||
- $\sigma(\cdot)$ 是非线性激活函数,例如 ReLU 或 tanh。
|
||
|
||
经过一层或多层图卷积后,可以得到最终的节点表示矩阵 $H^{(L)}$(或记为 $X$),维度为 $N \times d'$。
|
||
其中:
|
||
|
||
- 每一行 $x_i \in \mathbb{R}^{d'}$ 表示节点 $i$ 的空间特征,这些特征综合反映了其在网络拓扑中的位置及与邻居的关系。
|
||
|
||
#### 输出
|
||
|
||
- **GCN 输出**:形状为 $N \times d'$;若将模型用于时序建模,则对于每个时间步,都可以得到这样一个节点特征表示。
|
||
- 这里 $d'>d$ 。1.高维嵌入不仅保留了绝对位置信息,还包括了网络拓扑信息。2.兼容下游LSTM任务需求。
|
||
|
||
|
||
|
||
### LSTM 模块
|
||
|
||
#### 输入数据构造
|
||
|
||
在时序预测中,对于每个节点,我们通常有一段历史数据序列。假设我们采集了最近 $T$ 个时刻的数据,然后采用“滑动窗口”的方式,预测 $T+1$、 $T+2$...
|
||
|
||
- 对于每个时刻 $t$,节点 $i$ 的空间特征 $x_i^{(t)} \in \mathbb{R}^{d'}$ 由 GCN 得到;
|
||
|
||
- 将这些特征按照时间顺序排列,得到一个序列:
|
||
$$
|
||
X_i = \bigl[ x_i^{(t-T+1)},\, x_i^{(t-T+2)},\, \dots,\, x_i^{(t)} \bigr] \quad \in \mathbb{R}^{T \times d'}.
|
||
$$
|
||
|
||
对于整个网络来说,可以将数据看作一个三维张量,维度为 $(N, T, d')$。
|
||
|
||
#### LSTM 内部运作
|
||
|
||
LSTM 通过内部门控机制(遗忘门 $f_t$、输入门 $i_t$ 和输出门 $o_t$)来更新其记忆状态 $C_t$ 和隐藏状态 $h_t$。公式如下
|
||
|
||
- **遗忘门**:
|
||
$$
|
||
f_t = \sigma(W_f [h_{t-1},\, x_t] + b_f)
|
||
$$
|
||
|
||
- **输入门和候选记忆**:
|
||
$$
|
||
i_t = \sigma(W_i [h_{t-1},\, x_t] + b_i) \quad,\quad \tilde{C}_t = \tanh(W_C [h_{t-1},\, x_t] + b_C)
|
||
$$
|
||
|
||
- **记忆更新**:
|
||
$$
|
||
C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t
|
||
$$
|
||
|
||
- **输出门和隐藏状态**:
|
||
$$
|
||
o_t = \sigma(W_o [h_{t-1},\, x_t] + b_o), \quad h_t = o_t \odot \tanh(C_t)
|
||
$$
|
||
|
||
|
||
|
||
其中,$x_t$ 在这里对应每个节点在时刻 $t$ 的 GCN 输出特征;
|
||
$[h_{t-1},\, x_t]$ 为连接后的向量;
|
||
|
||
LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$(其中 $d''$ 为 LSTM 的隐藏单元数)捕捉了时间上的依赖信息。
|
||
|
||
#### 输出与预测
|
||
|
||
最后,经过 LSTM 处理后,我们在最后一个时间步获得最终的隐藏状态 $h_t$ 或使用整个序列的输出;接着通过一个全连接层(FC层)将隐藏状态映射到最终的预测输出。
|
||
|
||
- **全连接层转换公式**:
|
||
$$
|
||
\hat{y}_i = W_{\text{fc}} \cdot h_t + b_{\text{fc}}
|
||
$$
|
||
|
||
其中,假设预测的是二维坐标(例如 $x$ 和 $y$ 坐标),$W_{\text{fc}} \in \mathbb{R}^{2 \times d''}$,输出 $\hat{y}_i \in \mathbb{R}^2$ 表示节点 $i$ 在未来某个时刻(或下一时刻)的预测坐标。
|
||
|
||
|
||
|
||
|
||
|
||
若整个网络有 $N$ 个节点,则最终预测结果的输出维度为 $N \times 2$(或 $N \times T' \times 2$,如果预测多个未来时刻)。
|
||
|
||
|
||
|
||
### 疑问
|
||
|
||
该论文可能有点问题,每个节点只能预测自身未来位置,无法获取全局位置信息。如果先LSTM后GCN可能可以!
|
||
|