1509 lines
44 KiB
Markdown
1509 lines
44 KiB
Markdown
## 力扣Hot 100题
|
||
|
||
### 杂项
|
||
|
||
- **最大值**:`Integer.MAX_VALUE`
|
||
- **最小值**:`Integer.MIN_VALUE`
|
||
|
||
|
||
|
||
#### **数组集合比较**
|
||
|
||
**`Arrays.equals(array1, array2)`**
|
||
|
||
- 用于比较两个数组是否相等(内容相同)。
|
||
|
||
- 支持多种类型的数组(如 `int[]`、`char[]`、`Object[]` 等)。
|
||
|
||
- ```java
|
||
int[] arr1 = {1, 2, 3};
|
||
int[] arr2 = {1, 2, 3};
|
||
boolean isEqual = Arrays.equals(arr1, arr2); // true
|
||
|
||
|
||
|
||
`Collections` 类本身没有直接提供类似 `Arrays.equals` 的方法来比较两个集合的内容是否相等。不过,Java 中的集合类(如 `List`、`Set`、`Map`)已经实现了 `equals` 方法
|
||
|
||
- ```java
|
||
List<Integer> list1 = Arrays.asList(1, 2, 3);
|
||
List<Integer> list2 = Arrays.asList(1, 2, 3);
|
||
List<Integer> list3 = Arrays.asList(3, 2, 1);
|
||
System.out.println(list1.equals(list2)); // true
|
||
System.out.println(list1.equals(list3)); // false(顺序不同)
|
||
```
|
||
|
||
|
||
|
||
**逻辑比较**
|
||
|
||
```java
|
||
boolean flag = false;
|
||
if (!flag) { //! 是 Java 中的逻辑非运算符,只能用于对布尔值取反。
|
||
System.out.println("flag 是 false");
|
||
}
|
||
|
||
if (flag == false) { //更常用!
|
||
System.out.println("flag 是 false");
|
||
}
|
||
//java中没有 if(not flag) 这种写法!
|
||
```
|
||
|
||
|
||
|
||
#### Character好用的方法
|
||
|
||
`Character.isDigit(char c)`用于判断一个字符是否是一个数字字符
|
||
|
||
`Character.isLetter(char c)`用于判断字符是否是一个字母(大小写字母都可以)。
|
||
|
||
`Character.isLowerCase(char c)`判断字符是否是小写字母。
|
||
|
||
`Character.toLowerCase(char c)`将字符转换为小写字母。
|
||
|
||
|
||
|
||
#### Integer好用的方法
|
||
|
||
`Integer.parseInt(String s)`:将字符串 `s` 解析为一个整数(`int`)。
|
||
|
||
`Integer.toString(int i)`:将 `int` 转换为字符串。
|
||
|
||
`Integer.compare(int a,int b)` 比较a和b的大小,内部实现:
|
||
|
||
```
|
||
public static int compare(int x, int y) {
|
||
return (x < y) ? -1 : ((x == y) ? 0 : 1);
|
||
}
|
||
```
|
||
|
||
避免了 **整数溢出** 的风险,在排序中建议使用`Integer.compare(int a,int b)`代替 `a-b`
|
||
|
||
|
||
|
||
### 常用数据结构
|
||
|
||
#### String
|
||
|
||
子串:字符串中**连续的一段字符**。
|
||
|
||
子序列:字符串中**按顺序选取的一段字符**,可以不连续。
|
||
|
||
异位词:字母相同、字母频率相同、顺序不同,如`"listen"` 和 `"silent"`
|
||
|
||
|
||
|
||
排序:
|
||
|
||
需要String先转为char [] 数组,排序好之后再转为String类型!!
|
||
|
||
```java
|
||
char[] charArray = str.toCharArray();
|
||
Arrays.sort(charArray);
|
||
String sortedStr = new String(charArray);
|
||
```
|
||
|
||
|
||
|
||
取字符:
|
||
|
||
- `charAt(int index)` 方法返回指定索引处的 `char` 值。
|
||
- `char` 是基本数据类型,占用 2 个字节,表示一个 Unicode 字符。
|
||
- HashSet<Character> set = new HashSet<Character>();
|
||
|
||
取子串:
|
||
|
||
- `substring(int beginIndex, int endIndex)` 方法返回从 `beginIndex` 到 `endIndex - 1` 的子字符串。
|
||
- 返回的是 `String` 类型,即使子字符串只有一个字符。
|
||
|
||
|
||
|
||
#### StringBuffer
|
||
|
||
`StringBuffer` 是 Java 中用于操作可变字符串的类
|
||
|
||
```java
|
||
public class StringBufferExample {
|
||
public static void main(String[] args) {
|
||
// 创建初始字符串 "Hello"
|
||
StringBuffer sb = new StringBuffer("Hello");
|
||
System.out.println("Initial: " + sb.toString()); // 输出 "Hello"
|
||
|
||
// 1. append:在末尾追加 " World"
|
||
sb.append(" World");
|
||
System.out.println("After append: " + sb.toString()); // 输出 "Hello World"
|
||
|
||
// 2. insert:在索引 5 位置("Hello"后)插入 ", Java"
|
||
sb.insert(5, ", Java");
|
||
System.out.println("After insert: " + sb.toString()); // 输出 "Hello, Java World"
|
||
|
||
// 3. delete:删除从索引 5 到索引 11(不包含)的子字符串(即删除刚才插入的 ", Java")
|
||
sb.delete(5, 11);
|
||
//sb.delete(5, sb.length()); 删除到末尾
|
||
System.out.println("After delete: " + sb.toString()); // 输出 "Hello World"
|
||
|
||
// 4. deleteCharAt:删除索引 5 处的字符(删除空格)
|
||
sb.deleteCharAt(5);
|
||
System.out.println("After deleteCharAt: " + sb.toString()); // 输出 "HelloWorld"
|
||
|
||
// 5. reverse:反转整个字符串
|
||
sb.reverse();
|
||
System.out.println("After reverse: " + sb.toString()); // 输出 "dlroWolleH"
|
||
}
|
||
}
|
||
```
|
||
|
||
`StringBuffer`有库函数可以翻转,String未提供!
|
||
|
||
```java
|
||
StringBuilder sb = new StringBuilder(s);
|
||
String reversed = sb.reverse().toString();
|
||
```
|
||
|
||
StringBuffer清空内容:
|
||
|
||
```java
|
||
StringBuffer sb = new StringBuffer("Hello, world!");
|
||
System.out.println("Before clearing: " + sb);
|
||
// 清空 StringBuffer
|
||
sb.setLength(0);
|
||
```
|
||
|
||
`StringBuffer` 的 `append()` 方法不仅支持添加普通的字符串,也可以直接将另一个 `StringBuffer` 对象添加到当前的 `StringBuffer`。
|
||
|
||
|
||
|
||
#### HashMap
|
||
|
||
- 基于哈希表实现,查找、插入和删除的平均时间复杂度为 O(1)。
|
||
- 不保证元素的顺序。
|
||
|
||
```java
|
||
import java.util.HashMap;
|
||
import java.util.Map;
|
||
|
||
public class HashMapExample {
|
||
public static void main(String[] args) {
|
||
// 创建 HashMap
|
||
Map<String, Integer> map = new HashMap<>();
|
||
|
||
// 添加键值对
|
||
map.put("apple", 10);
|
||
map.put("banana", 20);
|
||
map.put("orange", 30);
|
||
|
||
// 获取值
|
||
int appleCount = map.get("apple"); //如果获取不存在的元素,返回null
|
||
System.out.println("Apple count: " + appleCount); // 输出 10
|
||
|
||
// 遍历 HashMap
|
||
for (Map.Entry<String, Integer> entry : map.entrySet()) {
|
||
System.out.println(entry.getKey() + ": " + entry.getValue());
|
||
}
|
||
// 输出:
|
||
// apple: 10
|
||
// banana: 20
|
||
// orange: 30
|
||
|
||
// 检查是否包含某个键
|
||
boolean containsBanana = map.containsKey("banana");
|
||
System.out.println("Contains banana: " + containsBanana); // 输出 true
|
||
|
||
// 删除键值对
|
||
map.remove("orange"); //删除不存在的元素也不会报错
|
||
System.out.println("After removal: " + map); // 输出 {apple=10, banana=20}
|
||
}
|
||
}
|
||
```
|
||
|
||
记录二维数组中某元素是否被访问过,推荐使用:
|
||
|
||
```java
|
||
int m = grid.length;
|
||
int n = grid[0].length;
|
||
boolean[][] visited = new boolean[m][n];
|
||
|
||
// 访问 (i, j) 时标记为已访问
|
||
visited[i][j] = true;
|
||
```
|
||
|
||
而非创建自定义Pair二元组作为键用Map记录。
|
||
|
||
|
||
|
||
#### HashSet
|
||
|
||
- 基于哈希表实现,查找、插入和删除的平均时间复杂度为 O(1)。
|
||
|
||
- 不保证元素的顺序!!因此不太用iterator迭代,而是用contains判断是否有xx元素。
|
||
|
||
```java
|
||
import java.util.HashSet;
|
||
import java.util.Set;
|
||
|
||
public class HashSetExample {
|
||
public static void main(String[] args) {
|
||
// 创建 HashSet
|
||
Set<Integer> set = new HashSet<>();
|
||
|
||
// 添加元素
|
||
set.add(10);
|
||
set.add(20);
|
||
set.add(30);
|
||
set.add(10); // 重复元素,不会被添加
|
||
|
||
// 检查元素是否存在
|
||
boolean contains20 = set.contains(20);
|
||
System.out.println("Contains 20: " + contains20); // 输出 true
|
||
|
||
// 遍历 HashSet
|
||
for (int num : set) {
|
||
System.out.println(num);
|
||
}
|
||
// 输出:
|
||
// 20
|
||
// 10
|
||
// 30
|
||
|
||
// 删除元素
|
||
set.remove(20);
|
||
System.out.println("After removal: " + set); // 输出 [10, 30]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### PriorityQueue
|
||
|
||
- 基于优先堆(最小堆或最大堆)实现,元素按优先级排序。
|
||
- **默认是最小堆**,即队首元素是最小的。 `new PriorityQueue<>(Comparator.reverseOrder());`定义最大堆
|
||
- 支持自定义排序规则,通过 `Comparator` 实现。
|
||
|
||
**常用方法:**
|
||
|
||
`add(E e)` / `offer(E e)`:
|
||
|
||
- 功能:将元素插入队列。
|
||
- 时间复杂度:`O(log n)`
|
||
- 区别
|
||
- `add`:当队列满时会抛出异常。
|
||
- `offer`:当队列满时返回 `false`,不会抛出异常。
|
||
|
||
`remove()` / `poll()`:
|
||
|
||
- 功能:移除并返回队首元素。
|
||
- 时间复杂度:`O(log n)`
|
||
- 区别
|
||
- `remove`:队列为空时抛出异常。
|
||
- `poll`:队列为空时返回 `null`。
|
||
|
||
`element()` / `peek()`:
|
||
|
||
- 功能:查看队首元素,但不移除。
|
||
- 时间复杂度:`O(1)`
|
||
- 区别
|
||
- `element`:队列为空时抛出异常。
|
||
- `peek`:队列为空时返回 `null`。
|
||
|
||
`clear()`:
|
||
|
||
- 功能:清空队列。
|
||
- 时间复杂度:`O(n)`(因为需要删除所有元素)
|
||
|
||
```java
|
||
import java.util.PriorityQueue;
|
||
import java.util.Comparator;
|
||
|
||
public class PriorityQueueExample {
|
||
public static void main(String[] args) {
|
||
// 创建 PriorityQueue(默认是最小堆)
|
||
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
|
||
|
||
// 添加元素
|
||
minHeap.add(10);
|
||
minHeap.add(20);
|
||
minHeap.add(5);
|
||
|
||
// 查看队首元素
|
||
System.out.println("队首元素: " + minHeap.peek()); // 输出 5
|
||
|
||
// 遍历 PriorityQueue(注意:遍历顺序不保证有序)
|
||
System.out.println("遍历 PriorityQueue:");
|
||
for (int num : minHeap) {
|
||
System.out.println(num);
|
||
}
|
||
// 输出:
|
||
// 5
|
||
// 10
|
||
// 20
|
||
|
||
// 移除队首元素
|
||
System.out.println("移除队首元素: " + minHeap.poll()); // 输出 5
|
||
|
||
// 再次查看队首元素
|
||
System.out.println("队首元素: " + minHeap.peek()); // 输出 10
|
||
|
||
// 创建最大堆(通过自定义 Comparator)
|
||
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
|
||
maxHeap.add(10);
|
||
maxHeap.add(20);
|
||
maxHeap.add(5);
|
||
|
||
// 查看队首元素
|
||
System.out.println("最大堆队首元素: " + maxHeap.peek()); // 输出 20
|
||
|
||
// 清空队列
|
||
minHeap.clear();
|
||
System.out.println("队列是否为空: " + minHeap.isEmpty()); // 输出 true
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
**自定义排序:按第二个元素的值构建小根堆**
|
||
|
||
如何比较器返回负数,则第一个数排在前面->优先级高->在堆顶
|
||
|
||
```java
|
||
public class CustomPriorityQueue {
|
||
public static void main(String[] args) {
|
||
// 定义一个 PriorityQueue,其中每个元素是 int[],并且按照数组第二个元素升序排列
|
||
PriorityQueue<int[]> minHeap = new PriorityQueue<>(
|
||
(a, b) -> return a[i]-b[i];
|
||
);
|
||
|
||
// 添加数组
|
||
minHeap.offer(new int[]{1, 2});
|
||
minHeap.offer(new int[]{3, 4});
|
||
minHeap.offer(new int[]{0, 5});
|
||
|
||
// 依次取出元素,输出结果
|
||
while (!minHeap.isEmpty()) {
|
||
int[] arr = minHeap.poll();
|
||
System.out.println(Arrays.toString(arr));
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
不用lambda版本:
|
||
|
||
```java
|
||
PriorityQueue<int[]> minHeap = new PriorityQueue<>(new Comparator<int[]>() {
|
||
@Override
|
||
public int compare(int[] a, int[] b) {
|
||
return a[1] - b[1];
|
||
}
|
||
});
|
||
```
|
||
|
||
|
||
|
||
##### **自己实现小根堆:**
|
||
|
||
**父节点**:对于任意索引 `i`,其父节点的索引为 `(i - 1) // 2`。
|
||
|
||
**左子节点**:索引为 `i` 的节点,其左子节点的索引为 `2 * i + 1`。
|
||
|
||
**右子节点**:索引为 `i` 的节点,其右子节点的索引为 `2 * i + 2`。
|
||
|
||
**上滤与下滤操作**
|
||
|
||
- **上滤**(Sift-Up):
|
||
用于插入操作。将新加入的元素与其父节点不断比较,若小于父节点则交换,直到满足堆序性质。
|
||
- **下滤**(Sift-Down):
|
||
用于删除操作或建堆。将根节点或某个节点与其子节点中较小的进行比较,若大于子节点则交换,直至满足堆序性质。
|
||
|
||
**建堆:**从数组中最后一个非叶节点开始(索引为 `heapSize/2 - 1`),对每个节点执行**下滤**操作(sift-down)
|
||
|
||
**插入元素:**将新元素插入到堆的末尾,然后执行**上滤**操作(sift-up),以保持堆序性质。
|
||
|
||
**弹出元素(删除堆顶):**弹出操作一般是删除堆顶元素(小根堆中即最小值),然后用堆尾元素替代堆顶,再进行**下滤**操作。
|
||
|
||
|
||
|
||
```java
|
||
class MinHeap {
|
||
private int[] heap; // 数组存储堆元素
|
||
private int size; // 当前堆中元素的个数
|
||
|
||
// 构造函数,初始化堆,capacity为堆的最大容量
|
||
public MinHeap(int capacity) {
|
||
heap = new int[capacity];
|
||
size = 0;
|
||
}
|
||
|
||
// 插入元素:先将新元素添加到数组末尾,然后执行上滤操作恢复堆序性质
|
||
public void insert(int value) {
|
||
if (size >= heap.length) {
|
||
throw new RuntimeException("Heap is full");
|
||
}
|
||
// 将新元素放到末尾
|
||
heap[size] = value;
|
||
int i = size;
|
||
size++;
|
||
|
||
// 上滤操作:不断与父节点比较,若新元素小于父节点则交换
|
||
while (i > 0) {
|
||
int parent = (i - 1) / 2;
|
||
if (heap[i] < heap[parent]) {
|
||
swap(heap, i, parent);
|
||
i = parent;
|
||
} else {
|
||
break;
|
||
}
|
||
}
|
||
}
|
||
|
||
// 弹出堆顶元素:移除堆顶(最小值),用最后一个元素替换堆顶,然后下滤恢复堆序
|
||
public int pop() {
|
||
if (size == 0) {
|
||
throw new RuntimeException("Heap is empty");
|
||
}
|
||
int min = heap[0];
|
||
// 将最后一个元素移到堆顶
|
||
heap[0] = heap[size - 1];
|
||
size--;
|
||
// 对新的堆顶执行下滤操作,恢复堆序性质
|
||
minHeapify(heap, 0, size);
|
||
return min;
|
||
}
|
||
|
||
// 建堆:将无序数组a构造成小根堆,heapSize为数组长度
|
||
public static void buildMinHeap(int[] a, int heapSize) {
|
||
for (int i = heapSize / 2 - 1; i >= 0; --i) {
|
||
minHeapify(a, i, heapSize);
|
||
}
|
||
}
|
||
|
||
// 下滤操作:从索引i开始,将子树调整为小根堆
|
||
public static void minHeapify(int[] a, int i, int heapSize) {
|
||
int l = 2 * i + 1, r = 2 * i + 2;
|
||
int smallest = i;
|
||
// 判断左子节点是否存在且比当前节点小
|
||
if (l < heapSize && a[l] < a[smallest]) {
|
||
smallest = l;
|
||
}
|
||
// 判断右子节点是否存在且比当前最小节点小
|
||
if (r < heapSize && a[r] < a[smallest]) {
|
||
smallest = r;
|
||
}
|
||
// 如果最小值不是当前节点,交换后继续对被交换的子节点执行下滤操作
|
||
if (smallest != i) {
|
||
swap(a, i, smallest);
|
||
minHeapify(a, smallest, heapSize);
|
||
}
|
||
}
|
||
|
||
// 交换数组中两个位置的元素
|
||
public static void swap(int[] a, int i, int j) {
|
||
int temp = a[i];
|
||
a[i] = a[j];
|
||
a[j] = temp;
|
||
}
|
||
|
||
}
|
||
|
||
```
|
||
|
||
改为大根堆只需要把里面 ''<'' 符号改为 ''>''
|
||
|
||
|
||
|
||
#### **ArrayList**
|
||
|
||
- 基于数组实现,支持动态扩展。
|
||
- 访问元素的时间复杂度为 O(1),在末尾插入和删除的时间复杂度为 O(1)。
|
||
- 在指定位置插入和删除O(n) `add(int index, E element)` `remove(int index)`
|
||
|
||
复制链表(list set queue都有addAll方法,map是putAll):
|
||
|
||
```java
|
||
List<Integer> list1 = new ArrayList<>();
|
||
// 假设 list1 中已有数据
|
||
List<Integer> list2 = new ArrayList<>();
|
||
list2.addAll(list1); //法一
|
||
List<Integer> list2 = new ArrayList<>(list1); //法二
|
||
```
|
||
|
||
清空(list set map queue map都有clear方法):
|
||
|
||
```java
|
||
List<Integer> list = new ArrayList<>();
|
||
// 清空 list
|
||
list.clear();
|
||
```
|
||
|
||
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.List;
|
||
|
||
public class ArrayListExample {
|
||
public static void main(String[] args) {
|
||
// 创建 ArrayList
|
||
List<Integer> list = new ArrayList<>();
|
||
|
||
// 添加元素
|
||
list.add(10);
|
||
list.add(20);
|
||
list.add(30);
|
||
|
||
int size = list.size(); // 获取列表大小
|
||
System.out.println("Size of list: " + size); // 输出 3
|
||
|
||
// 获取元素
|
||
int firstElement = list.get(0);
|
||
System.out.println("First element: " + firstElement); // 输出 10
|
||
|
||
// 修改元素
|
||
list.set(1, 25); // 将第二个元素改为 25
|
||
System.out.println("After modification: " + list); // 输出 [10, 25, 30]
|
||
|
||
// 遍历 ArrayList
|
||
for (int num : list) {
|
||
System.out.println(num);
|
||
}
|
||
// 输出:
|
||
// 10
|
||
// 25
|
||
// 30
|
||
|
||
// 删除元素
|
||
list.remove(2); // 删除第三个元素
|
||
System.out.println("After removal: " + list); // 输出 [10, 25]
|
||
}
|
||
}
|
||
```
|
||
|
||
**如果事先不知道嵌套列表的大小如何遍历呢?**
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.List;
|
||
|
||
int rows = 3;
|
||
int cols = 3;
|
||
List<List<Integer>> list = new ArrayList<>();
|
||
|
||
|
||
for (List<Integer> row : list) {
|
||
for (int num : row) {
|
||
System.out.print(num + " ");
|
||
}
|
||
System.out.println(); // 换行
|
||
}
|
||
for (int i = 0; i < list.size(); i++) {
|
||
List<Integer> row = list.get(i);
|
||
for (int j = 0; j < row.size(); j++) {
|
||
System.out.print(row.get(j) + " ");
|
||
}
|
||
System.out.println(); // 换行
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
#### **数组(Array)**
|
||
|
||
数组是一种固定长度的数据结构,用于存储相同类型的元素。数组的特点包括:
|
||
|
||
- **固定长度**:数组的长度在创建时确定,无法动态扩展。
|
||
- **快速访问**:通过索引访问元素的时间复杂度为 O(1)。
|
||
- **连续内存**:数组的元素在内存中是连续存储的。
|
||
|
||
```java
|
||
public class ArrayExample {
|
||
public static void main(String[] args) {
|
||
// 创建数组
|
||
int[] array = new int[5]; // 创建一个长度为 5 的整型数组
|
||
|
||
// 添加元素
|
||
array[0] = 10;
|
||
array[1] = 20;
|
||
array[2] = 30;
|
||
array[3] = 40;
|
||
array[4] = 50;
|
||
|
||
// 获取元素
|
||
int firstElement = array[0];
|
||
System.out.println("First element: " + firstElement); // 输出 10
|
||
|
||
// 修改元素
|
||
array[1] = 25; // 将第二个元素改为 25
|
||
System.out.println("After modification:");
|
||
for (int num : array) {
|
||
System.out.println(num);
|
||
}
|
||
// 输出:
|
||
// 10
|
||
// 25
|
||
// 30
|
||
// 40
|
||
// 50
|
||
|
||
// 遍历数组
|
||
System.out.println("Iterating through array:");
|
||
for (int i = 0; i < array.length; i++) {
|
||
System.out.println("Index " + i + ": " + array[i]);
|
||
}
|
||
// 输出:
|
||
// Index 0: 10
|
||
// Index 1: 25
|
||
// Index 2: 30
|
||
// Index 3: 40
|
||
// Index 4: 50
|
||
|
||
// 删除元素(数组长度固定,无法直接删除,可以通过覆盖实现)
|
||
int indexToRemove = 2; // 要删除的元素的索引
|
||
for (int i = indexToRemove; i < array.length - 1; i++) {
|
||
array[i] = array[i + 1]; // 将后面的元素向前移动
|
||
}
|
||
array[array.length - 1] = 0; // 最后一个元素置为 0(或其他默认值)
|
||
System.out.println("After removal:");
|
||
for (int num : array) {
|
||
System.out.println(num);
|
||
}
|
||
// 输出:
|
||
// 10
|
||
// 25
|
||
// 40
|
||
// 50
|
||
// 0
|
||
|
||
// 数组长度
|
||
int length = array.length;
|
||
System.out.println("Array length: " + length); // 输出 5
|
||
}
|
||
}
|
||
```
|
||
|
||
复制数组:
|
||
|
||
```
|
||
int[] source = {1, 2, 3, 4, 5};
|
||
int[] destination = Arrays.copyOf(source, source.length);
|
||
int[] partialArray = Arrays.copyOfRange(source, 1, 4); //复制指定元素,不包括索引4
|
||
```
|
||
|
||
初始化:
|
||
|
||
```
|
||
int[] memo = new int[nums.length];
|
||
Arrays.fill(memo, -1);
|
||
```
|
||
|
||
|
||
|
||
#### 二维数组
|
||
|
||
```java
|
||
int rows = 3;
|
||
int cols = 3;
|
||
int[][] array = new int[rows][cols];
|
||
// 填充数据
|
||
for (int i = 0; i < rows; i++) {
|
||
for (int j = 0; j < cols; j++) {
|
||
array[i][j] = i * cols + j + 1;
|
||
}
|
||
}
|
||
//创建并初始化
|
||
int[][] array = {
|
||
{1, 2, 3},
|
||
{4, 5, 6},
|
||
{7, 8, 9}
|
||
};
|
||
|
||
// 遍历二维数组,不知道几行几列
|
||
public void setZeroes(int[][] matrix) {
|
||
// 遍历每一行
|
||
for (int i = 0; i < matrix.length; i++) {
|
||
// 遍历当前行的每一列
|
||
for (int j = 0; j < matrix[i].length; j++) {
|
||
// 这里可以处理 matrix[i][j] 的元素
|
||
System.out.print(matrix[i][j] + " ");
|
||
}
|
||
System.out.println(); // 换行,便于输出格式化
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
#### Queue
|
||
|
||
队尾插入,队头取!
|
||
|
||
```java
|
||
import java.util.Queue;
|
||
import java.util.LinkedList;
|
||
|
||
public class QueueExample {
|
||
public static void main(String[] args) {
|
||
// 创建一个队列
|
||
Queue<Integer> queue = new LinkedList<>();
|
||
|
||
// 添加元素到队列中
|
||
queue.add(10); // 使用 add() 方法添加元素
|
||
queue.offer(20); // 使用 offer() 方法添加元素
|
||
queue.add(30);
|
||
System.out.println("队列内容:" + queue);
|
||
|
||
// 查看队头元素,不移除
|
||
int head = queue.peek();
|
||
System.out.println("队头元素(peek): " + head);
|
||
|
||
// 移除队头元素
|
||
int removed = queue.poll();
|
||
System.out.println("移除的队头元素(poll): " + removed);
|
||
System.out.println("队列内容:" + queue);
|
||
|
||
// 再次移除队头元素
|
||
int removed2 = queue.remove();
|
||
System.out.println("移除的队头元素(remove): " + removed2);
|
||
System.out.println("队列内容:" + queue);
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
#### Deque(双端队列+栈)
|
||
|
||
支持在队列的两端(头和尾)进行元素的插入和删除。这使得 Deque 既能作为队列(FIFO)又能作为栈(LIFO)使用。
|
||
|
||
建议在需要栈操作时使用 `Deque` 的实现
|
||
|
||
**栈**
|
||
|
||
```java
|
||
Deque<Integer> stack = new ArrayDeque<>();
|
||
//Deque<Integer> stack = new LinkedList<>();
|
||
stack.push(1); // 入栈
|
||
Integer top1=stack.peek()
|
||
Integer top = stack.pop(); // 出栈
|
||
```
|
||
|
||
- **LinkedList** 是基于双向链表实现的,每个节点存储数据和指向前后节点的引用。
|
||
- **ArrayDeque** 则基于动态数组实现,内部使用循环数组来存储数据。
|
||
- **ArrayDeque** 在大多数情况下性能更好,因为数组在内存中连续,缓存友好,且操作(如 push/pop)开销更小。
|
||
|
||
|
||
|
||
**双端队列**
|
||
|
||
*在队头操作*
|
||
|
||
- `addFirst(E e)`:在队头添加元素,如果操作失败会抛出异常。
|
||
- `offerFirst(E e)`:在队头插入元素,返回 `true` 或 `false` 表示是否成功。
|
||
- `peekFirst()`:查看队头元素,不移除;队列为空返回 `null`。
|
||
- `removeFirst()`:移除并返回队头元素;队列为空会抛出异常。
|
||
- `pollFirst()`:移除并返回队头元素;队列为空返回 `null`。
|
||
|
||
*在队尾操作*
|
||
|
||
- `addLast(E e)`:在队尾添加元素,若失败会抛出异常。
|
||
- `offerLast(E e)`:在队尾插入元素,返回 `true` 或 `false` 表示是否成功。
|
||
- `peekLast()`:查看队尾元素,不移除;队列为空返回 `null`。
|
||
- `removeLast()`:移除并返回队尾元素;队列为空会抛出异常。
|
||
- `pollLast()`:移除并返回队尾元素;队列为空返回 `null`。
|
||
|
||
|
||
|
||
*添加元素*:调用 `add(e)` 或 `offer(e)` 时,实际上是调用 `addLast(e)` 或 `offerLast(e)`,即在**队尾**添加元素。
|
||
|
||
*删除或查看元素*:调用 `remove()` 或 `poll()` 时,则是调用 `removeFirst()` 或 `pollFirst()`,即在队头移除元素;同理,`element()` 或 `peek()` 则是查看队头元素。
|
||
|
||
```java
|
||
import java.util.Deque;
|
||
import java.util.LinkedList;
|
||
|
||
public class DequeExample {
|
||
public static void main(String[] args) {
|
||
// 使用 LinkedList 实现双端队列
|
||
Deque<Integer> deque = new LinkedList<>();
|
||
|
||
// 在队列头部添加元素
|
||
deque.addFirst(10);
|
||
// 在队列尾部添加元素
|
||
deque.addLast(20);
|
||
// 在队列头部插入元素
|
||
deque.offerFirst(5);
|
||
// 在队列尾部插入元素
|
||
deque.offerLast(30);
|
||
|
||
System.out.println("双端队列内容:" + deque);
|
||
|
||
// 查看队头和队尾元素,不移除
|
||
int first = deque.peekFirst();
|
||
int last = deque.peekLast();
|
||
System.out.println("队头元素:" + first);
|
||
System.out.println("队尾元素:" + last);
|
||
|
||
// 从队头移除元素
|
||
int removedFirst = deque.removeFirst();
|
||
System.out.println("移除队头元素:" + removedFirst);
|
||
// 从队尾移除元素
|
||
int removedLast = deque.removeLast();
|
||
System.out.println("移除队尾元素:" + removedLast);
|
||
|
||
System.out.println("双端队列最终内容:" + deque);
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### Iterator
|
||
|
||
- **`HashMap`、`HashSet`、`ArrayList` 和 `PriorityQueue`** 都实现了 `Iterable` 接口,支持 `iterator()` 方法。
|
||
|
||
`Iterator` 接口中包含以下主要方法:
|
||
|
||
1. `hasNext()`:如果迭代器还有下一个元素,则返回 `true`,否则返回 `false`。
|
||
2. `next()`:返回迭代器的下一个元素,并将迭代器移动到下一个位置。
|
||
3. `remove()`:从迭代器当前位置删除元素。该方法是可选的,不是所有的迭代器都支持。
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.Iterator;
|
||
|
||
public class Main {
|
||
public static void main(String[] args) {
|
||
// 创建一个 ArrayList 集合
|
||
ArrayList<Integer> list = new ArrayList<>();
|
||
list.add(1);
|
||
list.add(2);
|
||
list.add(3);
|
||
|
||
// 获取集合的迭代器
|
||
Iterator<Integer> iterator = list.iterator();
|
||
|
||
// 使用迭代器遍历集合并输出元素
|
||
while (iterator.hasNext()) {
|
||
Integer element = iterator.next();
|
||
System.out.println(element);
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
### 排序
|
||
|
||
排序时间复杂度:O(nlog(n))
|
||
|
||
求最大值:O(n)
|
||
|
||
|
||
|
||
#### 快速排序
|
||
|
||
**基本思想:**
|
||
|
||
快速排序是一种基于“分治”思想的排序算法,通过选定一个“枢轴元素(pivot)”,将数组划分为左右两个子区间:左边都小于等于 pivot,右边都大于等于 pivot;然后对这两个子区间递归排序,最终使整个数组有序。
|
||
|
||
```java
|
||
public class QuickSortWithSwap {
|
||
|
||
// 交换数组中两个元素的位置
|
||
private static void swap(int[] arr, int i, int j) {
|
||
int temp = arr[i];
|
||
arr[i] = arr[j];
|
||
arr[j] = temp;
|
||
}
|
||
|
||
private static void quickSort(int[] arr, int low, int high) {
|
||
if (low < high) {
|
||
int pivotPos = partition(arr, low, high); // 划分
|
||
quickSort(arr, low, pivotPos - 1); // 递归排序左子表
|
||
quickSort(arr, pivotPos + 1, high); // 递归排序右子表
|
||
}
|
||
}
|
||
|
||
private static int partition(int[] arr, int low, int high) {
|
||
int pivot = arr[low]; // 选取第一个元素作为枢轴
|
||
int left = low; // 左指针
|
||
int right = high; // 右指针
|
||
|
||
while (left < right) {
|
||
// 从右向左找第一个小于枢轴的元素
|
||
while (left < right && arr[right] >= pivot) {
|
||
right--;
|
||
}
|
||
// 从左向右找第一个大于枢轴的元素
|
||
while (left < right && arr[left] <= pivot) {
|
||
left++;
|
||
}
|
||
// 交换这两个元素
|
||
if (left < right) {
|
||
swap(arr, left, right);
|
||
}
|
||
}
|
||
// 将枢轴放到最终位置
|
||
swap(arr, low, left);
|
||
return left; // 返回枢轴的位置
|
||
}
|
||
|
||
public static void main(String[] args) {
|
||
int[] arr = {49, 38, 65, 97, 76, 13, 27, 49};
|
||
|
||
quickSort(arr, 0, arr.length - 1);
|
||
|
||
System.out.println("\n排序后:");
|
||
for (int num : arr) {
|
||
System.out.print(num + " ");
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
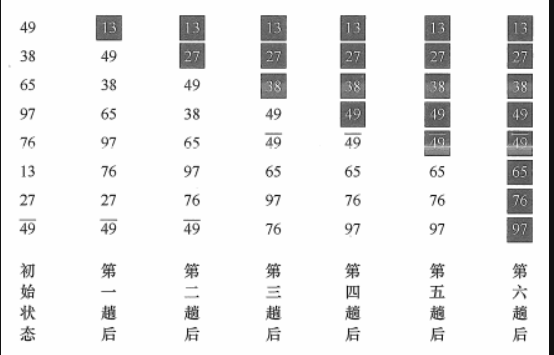
#### 冒泡排序
|
||
|
||
**基本思想:**
|
||
|
||
【每次将最小/大元素,通过依次交换顺序,放到首/尾位。】
|
||
|
||
- 从后往前(或从前往后)两两比较相邻元素的值,若为逆序, 则交换它们,直到序列比较完。我们称它为第一趟冒泡,结果是将最小的元素交换到待排序列的第一个位置(或将最大的元素交换到待排序列的最后一个位置);
|
||
- 下一趟冒泡时,前一趟确定的最小元素不再参与比较,每趟冒泡的结果是把序列中的最小元素(或最大元素)放到了序列的最终位置。
|
||
- ……这样最多做n - 1趟冒泡就能把所有元素排好序。
|
||
- 如若有一趟没有元素交换位置,则可提前说明已排好序。
|
||
|
||
|
||
|
||
|
||
```java
|
||
public void bubbleSort(int[] arr){
|
||
//n-1 趟冒泡
|
||
for (int i = 0; i < arr.length-1; i++) {
|
||
boolean flag=false;
|
||
//冒泡
|
||
for (int j = arr.length-1; j >i ; j--) {
|
||
if (arr[j-1]>arr[j]){
|
||
swap(arr,j-1,j);
|
||
flag=true;
|
||
}
|
||
}
|
||
//本趟遍历后没有发生交换,说明表已经有序
|
||
if (!flag){
|
||
return;
|
||
}
|
||
}
|
||
}
|
||
private void swap(int[] arr,int i,int j){
|
||
int temp=arr[i];
|
||
arr[i]=arr[j];
|
||
arr[j]=temp;
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### 归并排序
|
||
|
||
**基本思想:**
|
||
|
||
将待排序的数组视为多个有序子表,每个子表的长度为 1,通过两两归并逐步合并成一个有序数组。
|
||
|
||
**实现思路**
|
||
|
||
- 分解:递归地将数组拆分成两个子数组,直到每个子数组只有一个元素。
|
||
- 合并:将两个有序子数组合并为一个有序数组。
|
||
|
||
**时间复杂度**:
|
||
O(n log n),无论最坏、最好、平均情况。
|
||
|
||
```java
|
||
public class MergeSort {
|
||
|
||
/**
|
||
* 归并排序(入口函数)
|
||
* @param arr 待排序数组
|
||
*/
|
||
public static void mergeSort(int[] arr) {
|
||
if (arr == null || arr.length <= 1) {
|
||
return; // 边界条件
|
||
}
|
||
int[] temp = new int[arr.length]; // 辅助数组
|
||
mergeSort(arr, 0, arr.length - 1, temp);
|
||
}
|
||
|
||
private static void mergeSort(int[] arr, int left, int right, int[] temp) {
|
||
if (left < right) {
|
||
int mid = (right + left) / 2;
|
||
mergeSort(arr, left, mid, temp); // 递归左子数组
|
||
mergeSort(arr, mid + 1, right, temp); // 递归右子数组
|
||
merge(arr, left, mid, right, temp); // 合并两个有序子数组
|
||
}
|
||
}
|
||
|
||
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
|
||
int i = left; // 左子数组起始指针
|
||
int j = mid + 1; // 右子数组起始指针
|
||
int t = 0; // 辅助数组指针
|
||
|
||
// 1. 按序合并两个子数组到temp
|
||
while (i <= mid && j <= right) {
|
||
if (arr[i] <= arr[j]) { // 注意等号保证稳定性
|
||
temp[t++] = arr[i++];
|
||
} else {
|
||
temp[t++] = arr[j++];
|
||
}
|
||
}
|
||
|
||
// 2. 将剩余元素拷贝到temp
|
||
while (i <= mid) {
|
||
temp[t++] = arr[i++];
|
||
}
|
||
while (j <= right) {
|
||
temp[t++] = arr[j++];
|
||
}
|
||
|
||
// 3. 将temp中的数据复制回原数组
|
||
t = 0;
|
||
while (left <= right) {
|
||
arr[left++] = temp[t++];
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### **数组排序**
|
||
|
||
```java
|
||
import java.util.Arrays;
|
||
|
||
public class ArraySortExample {
|
||
public static void main(String[] args) {
|
||
int[] numbers = {5, 2, 9, 1, 5, 6};
|
||
Arrays.sort(numbers); // 对数组进行排序
|
||
System.out.println(Arrays.toString(numbers)); // 输出 [1, 2, 5, 5, 6, 9]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### 集合排序
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.Collections;
|
||
import java.util.List;
|
||
|
||
public class ListSortExample {
|
||
public static void main(String[] args) {
|
||
// 创建一个 ArrayList 并添加元素
|
||
List<Integer> numbers = new ArrayList<>();
|
||
numbers.add(5);
|
||
numbers.add(2);
|
||
numbers.add(9);
|
||
numbers.add(1);
|
||
numbers.add(5);
|
||
numbers.add(6);
|
||
|
||
// 对 List 进行排序
|
||
Collections.sort(numbers);
|
||
|
||
// 输出排序后的 List
|
||
System.out.println(numbers); // 输出 [1, 2, 5, 5, 6, 9]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### **自定义排序**
|
||
|
||
要实现接口自定义排序,必须实现 `Comparator<T>` 接口的 `compare(T o1, T o2)` 方法。
|
||
|
||
`Comparator` 接口中定义的 `compare(T o1, T o2)` 方法返回**一个整数**(非布尔值!!),这个整数的正负意义如下:
|
||
|
||
- 如果返回负数,说明 `o1` 排在 `o2`前面。
|
||
- 如果返回零,说明 `o1` 等于 `o2`。
|
||
- 如果返回正数,说明 `o1` 排在 `o2`后面。
|
||
|
||
|
||
|
||
**自定义比较器排序二维数组** 用Lambda表达式实现`Comparator<int[]>接口`
|
||
|
||
```java
|
||
import java.util.Arrays;
|
||
|
||
public class IntervalSort {
|
||
public static void main(String[] args) {
|
||
int[][] intervals = { {1, 3}, {2, 6}, {8, 10}, {15, 18} };
|
||
|
||
// 自定义比较器,先比较第一个元素,如果相等再比较第二个元素
|
||
Arrays.sort(intervals, (a, b) -> {
|
||
if (a[0] != b[0]) {
|
||
return Integer.compare(a[0], b[0]);
|
||
} else {
|
||
return Integer.compare(a[1], b[1]);
|
||
}
|
||
});
|
||
|
||
// 输出排序结果
|
||
for (int[] interval : intervals) {
|
||
System.out.println(Arrays.toString(interval));
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
对象排序,不用lambda方式
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.Collections;
|
||
import java.util.Comparator;
|
||
import java.util.List;
|
||
|
||
class Person {
|
||
String name;
|
||
int age;
|
||
|
||
public Person(String name, int age) {
|
||
this.name = name;
|
||
this.age = age;
|
||
}
|
||
|
||
@Override
|
||
public String toString() {
|
||
return name + " (" + age + ")";
|
||
}
|
||
}
|
||
|
||
public class ComparatorSortExample {
|
||
public static void main(String[] args) {
|
||
// 创建一个 Person 列表
|
||
List<Person> people = new ArrayList<>();
|
||
people.add(new Person("Alice", 25));
|
||
people.add(new Person("Bob", 20));
|
||
people.add(new Person("Charlie", 30));
|
||
|
||
// 使用 Comparator 按姓名排序,匿名内部类形式
|
||
Collections.sort(people, new Comparator<Person>() {
|
||
@Override
|
||
public int compare(Person p1, Person p2) {
|
||
return p1.name.compareTo(p2.name); // 按姓名升序排序
|
||
}
|
||
});
|
||
|
||
// 使用 Comparator 按姓名排序,使用 lambda 表达式
|
||
//Collections.sort(people, (p1, p2) -> p1.name.compareTo(p2.name));
|
||
|
||
// 输出排序后的列表
|
||
System.out.println(people); // 输出 [Alice (25), Bob (20), Charlie (30)]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
### 题型
|
||
|
||
常见术语:
|
||
|
||
子串(Substring):子字符串 是字符串中连续的 非空 字符序列
|
||
|
||
回文串(Palindrome):回文 串是向前和向后读都相同的字符串。
|
||
|
||
子序列((Subsequence)):可以通过删除原字符串中任意个字符(不改变剩余字符的相对顺序)得到的序列,不要求连续。例如 "abc" 的 "ac" 就是一个子序列。
|
||
|
||
前缀 (Prefix) :从字符串起始位置开始的连续字符序列,如 "leetcode" 的前缀 "lee"。
|
||
|
||
字母异位词 (Anagram):由相同字符组成但排列顺序不同的字符串。例如 "abc" 与 "cab" 就是异位词。
|
||
|
||
子集、幂集:数组的 子集 是从数组中选择一些元素(可能为空)。例如,对于集合 S = {1, 2},其幂集为:
|
||
{ ∅, {1}, {2}, {1, 2} },子集有{1}
|
||
|
||
|
||
|
||
#### 哈希
|
||
|
||
**问题分析**:
|
||
|
||
- 确定是否需要快速查找或存储数据。
|
||
- 判断是否需要统计元素频率或检查元素是否存在。
|
||
|
||
**适用场景**
|
||
|
||
1. **快速查找**:
|
||
- 当需要频繁查找元素时,哈希表可以提供 O(1) 的平均时间复杂度。
|
||
2. **统计频率**:
|
||
- 统计元素出现次数时,哈希表是常用工具。
|
||
3. **去重**:
|
||
- 需要去除重复元素时,`HashSet` 可以有效实现。
|
||
|
||
#### 双指针
|
||
|
||
题型:
|
||
|
||
- 同向双指针:两个指针从同一侧开始移动,通常用于**滑动窗口**或链表问题。
|
||
- 对向双指针:两个指针从两端向中间移动,通常用于有序数组或回文问题。重点是考虑**移动哪个指针**可能优化结果!!!
|
||
- 快慢指针:两个指针以不同速度移动,通常用于链表中的环检测或中点查找。
|
||
|
||
适用场景:
|
||
|
||
**有序数组的两数之和**:
|
||
|
||
- 在对向双指针的帮助下,可以在 O(n) 时间内找到两个数,使它们的和等于目标值。
|
||
|
||
**滑动窗口**:
|
||
|
||
- 用于解决**子数组或子字符串**问题,如同向双指针可以在 O(n) 时间内找到满足条件的最短或最长子数组。
|
||
|
||
**链表中的环检测**:
|
||
|
||
- 快慢指针可以用于检测链表中是否存在环,并找到环的起点。
|
||
|
||
**回文问题**:
|
||
|
||
- 对向双指针可以用于判断字符串或数组是否是回文。
|
||
|
||
**合并有序数组或链表**:
|
||
|
||
- 双指针可以用于合并两个有序数组或链表,时间复杂度为 O(n)。
|
||
|
||
|
||
|
||
#### 前缀和
|
||
|
||
1. **前缀和的定义**
|
||
定义前缀和 `preSum[i]` 为数组 `nums` 从索引 0 到 i 的元素和,即
|
||
$$
|
||
\text{preSum}[i] = \sum_{j=0}^{i} \text{nums}[j]
|
||
$$
|
||
|
||
2. **子数组和的关系**
|
||
对于任意子数组 `nums[i+1..j]`(其中 `0 ≤ i < j < n`),其和可以表示为
|
||
$$
|
||
\text{sum}(i+1,j) = \text{preSum}[j] - \text{preSum}[i]
|
||
$$
|
||
当这个子数组的和等于 k 时,有
|
||
$$
|
||
\text{preSum}[j] - \text{preSum}[i] = k
|
||
$$
|
||
即
|
||
$$
|
||
\text{preSum}[i] = \text{preSum}[j] - k
|
||
$$
|
||
$\text{preSum}[j] - k$表示 "以当前位置结尾的子数组和为k"
|
||
|
||
3. **利用哈希表存储前缀和**
|
||
我们可以使用一个哈希表 `prefix` 来存储每个**前缀和**出现的**次数**。
|
||
|
||
- 初始时,`prefix[0] = 1`,表示前缀和为 0 出现一次(对应空前缀)。
|
||
- 遍历数组,每计算一个新的前缀和 `preSum`,就查看 `preSum - k` 是否在哈希表中。如果存在,则说明之前有一个前缀和等于 `preSum - k`,那么从该位置后一个位置到**当前索引**的子数组和为 k,累加其出现的次数。
|
||
|
||
4. **时间复杂度**
|
||
该方法只需要遍历数组一次,时间复杂度为 O(n)。
|
||
|
||
|
||
|
||
#### **遍历二叉树**
|
||
|
||
*递归法中序*
|
||
|
||
```java
|
||
public void inOrderTraversal(TreeNode root, List<Integer> list) {
|
||
if (root != null) {
|
||
inOrderTraversal(root.left, list); // 遍历左子树
|
||
list.add(root.val); // 访问当前节点
|
||
inOrderTraversal(root.right, list); // 遍历右子树
|
||
}
|
||
}
|
||
```
|
||
|
||
*迭代法中序*
|
||
|
||
```java
|
||
public void inOrderTraversalIterative(TreeNode root, List<Integer> list) {
|
||
Deque<TreeNode> stack = new ArrayDeque<>();
|
||
TreeNode curr = root;
|
||
|
||
while (curr != null || !stack.isEmpty()) {
|
||
// 一路向左入栈
|
||
while (curr != null) {
|
||
stack.push(curr); // push = addFirst
|
||
curr = curr.left;
|
||
}
|
||
|
||
// 弹出栈顶并访问
|
||
curr = stack.pop(); // pop = removeFirst
|
||
list.add(curr.val);
|
||
|
||
// 转向右子树
|
||
curr = curr.right;
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
*迭代法前序*
|
||
|
||
```java
|
||
public void preOrderTraversalIterative(TreeNode root, List<Integer> list) {
|
||
if (root == null) return;
|
||
|
||
Deque<TreeNode> stack = new ArrayDeque<>();
|
||
stack.push(root);
|
||
|
||
while (!stack.isEmpty()) {
|
||
TreeNode node = stack.pop();
|
||
list.add(node.val); // 先访问当前节点
|
||
|
||
// 注意:先压右子节点,再压左子节点
|
||
// 因为栈是“后进先出”的,先弹出的是左子节点
|
||
if (node.right != null) {
|
||
stack.push(node.right);
|
||
}
|
||
if (node.left != null) {
|
||
stack.push(node.left);
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
层序遍历BFS
|
||
|
||
```java
|
||
public List<List<Integer>> levelOrder(TreeNode root) {
|
||
List<List<Integer>> result = new ArrayList<>();
|
||
if (root == null) return result;
|
||
|
||
Queue<TreeNode> queue = new LinkedList<>();
|
||
queue.offer(root);
|
||
|
||
while (!queue.isEmpty()) {
|
||
int levelSize = queue.size();
|
||
List<Integer> level = new ArrayList<>();
|
||
|
||
for (int i = 0; i < levelSize; i++) {
|
||
TreeNode node = queue.poll();
|
||
level.add(node.val);
|
||
|
||
if (node.left != null) {
|
||
queue.offer(node.left);
|
||
}
|
||
if (node.right != null) {
|
||
queue.offer(node.right);
|
||
}
|
||
}
|
||
result.add(level);
|
||
}
|
||
|
||
return result;
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### 回溯法
|
||
|
||
回溯算法用于 **搜索一个问题的所有的解** ,即爆搜(暴力解法),通过深度优先遍历的思想实现。核心思想是:
|
||
|
||
**1.逐步构建解答:**
|
||
|
||
回溯算法通过逐步构造候选解,当构造的部分解满足条件时继续扩展;如果发现当前解不符合要求,则“回溯”到上一步,尝试其他可能性。
|
||
|
||
**2.剪枝(Pruning):**
|
||
|
||
在构造候选解的过程中,算法会判断当前部分解是否有可能扩展成最终的有效解。如果判断出无论如何扩展都不可能得到正确解,就立即停止继续扩展该分支,从而节省计算资源。
|
||
|
||
**3.递归调用**
|
||
|
||
回溯通常通过递归来实现。递归函数在**每一层都尝试不同的选择**,并在尝试失败或达到终点时返回上一层重新尝试其他选择。
|
||
|
||
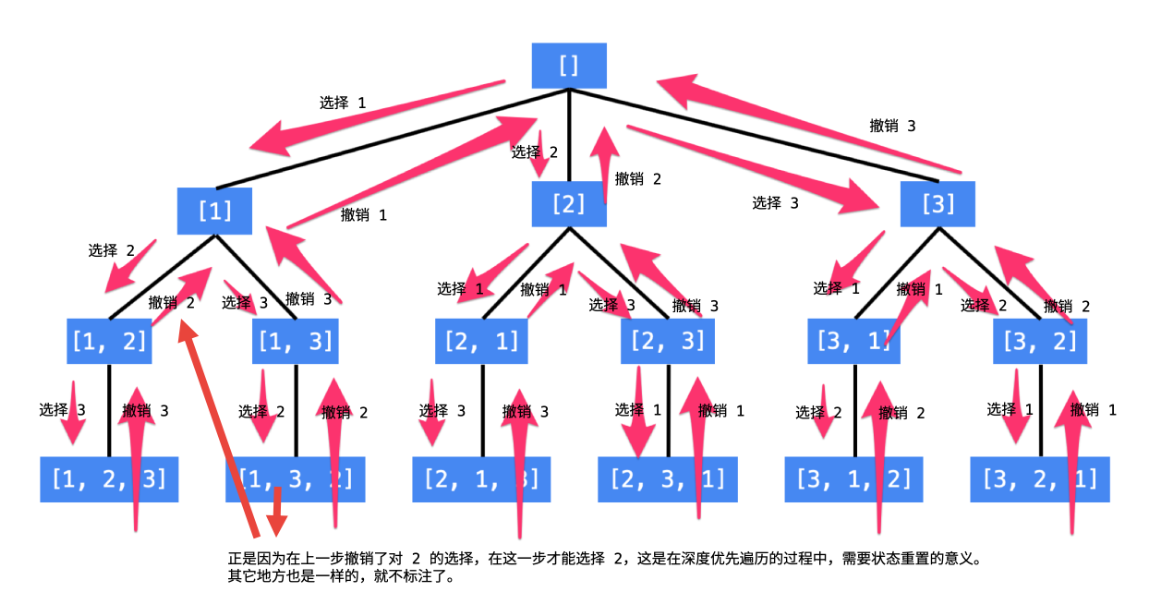
**例:以数组 `[1, 2, 3]` 的全排列为例。**
|
||
|
||
先写以 1 开头的全排列,它们是:`[1, 2, 3], [1, 3, 2]`,即 `1` + `[2, 3]` 的全排列(注意:递归结构体现在这里);
|
||
再写以 2 开头的全排列,它们是:`[2, 1, 3]`, `[2, 3, 1]`,即 `2` + `[1, 3]` 的全排列;
|
||
最后写以 3 开头的全排列,它们是:`[3, 1, 2]`, `[3, 2, 1]`,即 `3` + `[1, 2]` 的全排列。
|
||
|
||
|
||
|
||
```java
|
||
public class Permute {
|
||
public List<List<Integer>> permute(int[] nums) {
|
||
List<List<Integer>> res = new ArrayList<>();
|
||
// 用来标记数组中数字是否被使用
|
||
boolean[] used = new boolean[nums.length];
|
||
List<Integer> path = new ArrayList<>();
|
||
backtrack(nums, used, path, res);
|
||
return res;
|
||
}
|
||
|
||
private void backtrack(int[] nums, boolean[] used, List<Integer> path, List<List<Integer>> res) {
|
||
// 当path中元素个数等于nums数组的长度时,说明已构造出一个排列
|
||
if (path.size() == nums.length) {
|
||
res.add(new ArrayList<>(path));
|
||
return;
|
||
}
|
||
// 遍历数组中的每个数字
|
||
for (int i = 0; i < nums.length; i++) {
|
||
// 如果该数字已经在当前排列中使用过,则跳过
|
||
if (used[i]) {
|
||
continue;
|
||
}
|
||
// 选择数字nums[i]
|
||
used[i] = true;
|
||
path.add(nums[i]);
|
||
// 递归构造剩余的排列
|
||
backtrack(nums, used, path, res);
|
||
// 回溯:撤销选择,尝试其他数字
|
||
path.remove(path.size() - 1);
|
||
used[i] = false;
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
#### 大小根堆
|
||
|
||
**题目描述**:给定一个整数数组 `nums` 和一个整数 `k`,返回出现频率最高的前 `k` 个元素,返回顺序可以任意。
|
||
|
||
**解法一:大根堆(最大堆)**
|
||
|
||
**思路**:
|
||
|
||
1. 使用 `HashMap` 统计每个元素的出现频率。
|
||
2. 构建一个**大根堆**(`PriorityQueue` + 自定义比较器),根据频率降序排列。
|
||
3. 将所有元素加入堆中,**弹出前 `k` 个元素**即为答案。
|
||
|
||
**适合场景**:
|
||
|
||
- 实现简单,适用于对全部元素排序后取前 `k` 个。
|
||
- 时间复杂度:**O(n log n)**,因为需要将所有 `n` 个元素都加入堆。
|
||
|
||
------
|
||
|
||
**解法二:小根堆(最小堆)**
|
||
|
||
**思路**:
|
||
|
||
1. 使用 `HashMap` 统计频率。
|
||
2. 构建一个**小根堆**,堆中仅保存前 `k` 个高频元素。
|
||
3. 遍历每个元素:
|
||
- 如果堆未满,直接加入。
|
||
- 如果当前元素频率大于堆顶(最小频率),则弹出堆顶,加入当前元素。
|
||
4. 最终堆中保存的就是前 `k` 个高频元素。
|
||
|
||
| 方法 | 适合场景 | 时间复杂度 | 空间复杂度 |
|
||
| ------ | --------------- | ---------- | ---------- |
|
||
| 大根堆 | k ≈ n,简单易写 | O(n log n) | O(n) |
|
||
| 小根堆 | k ≪ n,更高效 | O(n log k) | O(n) |
|