zy123/md_files
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity
md_files/科研/高飞论文.md

14 KiB
Raw Blame History

高飞论文

证明特征值序列为平稳的时间序列

问题设定

  • 研究对象
    设 \{\lambda_1(A)_t\}_{t\in\mathbb Z} 是随时间变化的随机对称矩阵 A_t 的最大特征值序列（如动态网络的邻接矩阵）。
  • 目标
    证明 \{\lambda_1(A)_t\} 是 二阶（弱）平稳的时间序列，即
    1. $E[\lambda_1(A)_t]=\mu_1$（与 t 无关）；
    2. $\operatorname{Var}[\lambda_1(A)_t]=\sigma_1^2<\infty$（与 t 无关）；
    3. \operatorname{Cov}(\lambda_1(A)_t,\lambda_1(A)_{t-k})=\gamma(k) 只依赖滞后 $k$。

关键假设

  • 矩阵统计特性（引理 1）

    • A_t 为 N\times N 实对称随机矩阵；元素 \{a_{ij}\}_{i\le j} 相互独立且有界：$|a_{ij}|\le K$。

    • 非对角元素：$E[a_{ij}]=\mu>0,\ \operatorname{Var}(a_{ij})=\sigma^2$；对角元素：$E[a_{ii}]=v$。

    • N 足够大时

      
E[\lambda_1(A_t)]\approx(N-1)\mu+v+\tfrac{\sigma^2}{\mu}\equiv\mu_1,\qquad
\operatorname{Var}[\lambda_1(A_t)]\approx2\sigma^2\equiv\sigma_1^2 .

说明：

  • $\sigma^2$
    这是随机矩阵 A_t 的非对角线元素 a_{ij} (i \neq j) 的方差，即

    
\text{Var}(a_{ij}) = \sigma^2.

    根据引理1的假设，所有非对角线元素独立同分布，均值为 $\mu$，方差为 $\sigma^2$。

  • $\sigma_1^2$
    这是最大特征值 \lambda_1(A_t) 的方差，即

    
\text{Var}[\lambda_1(A_t)] \equiv \sigma_1^2.

    当 N 足够大时，\sigma_1^2 近似为 $2\sigma^2$。

  • 时间序列模型
    对去中心化序列

    
  \tilde z_t:=\lambda_1(A)_t-\mu_1

    假设其服从 AR(1)

    
  \tilde z_t=\rho\,\tilde z_{t-1}+\varepsilon_t,\qquad
  \varepsilon_t\stackrel{\text{i.i.d.}}{\sim}\text{WN}(0,\sigma_\varepsilon^{2}),\ \ |\rho|<1,

    且 \varepsilon_t 与历史 \{\tilde z_{s}\}_{s<t} 独立。

证明主特征值序列平稳

(1) 均值恒定性的推导

  • 去中心化后 $E[\tilde z_t]=0$。因此 
    
  E[\lambda_1(A)_t]=E[\tilde z_t]+\mu_1=\mu_1,
    与 t 无关，满足第一条。

(2) 方差恒定

AR(1)模型定义为：


z_t = \rho z_{t-1} + \varepsilon_t


\begin{aligned}
z_t &= \varepsilon_t + \rho z_{t-1} \\
&= \varepsilon_t + \rho (\varepsilon_{t-1} + \rho z_{t-2}) \\
&= \varepsilon_t + \rho \varepsilon_{t-1} + \rho^2 \varepsilon_{t-2} + \cdots \\
&= \sum_{j=0}^\infty \rho^j \varepsilon_{t-j}
\end{aligned}


\text{Var}(z_t) = \text{Var}\left( \sum_{j=0}^\infty \rho^j \varepsilon_{t-j} \right)= \sum_{j=0}^\infty \rho^{2j} \text{Var}(\varepsilon_{t-j})

由于\text{Var}(\varepsilon_{t-j}) = \sigma_\varepsilon^2 对所有 j 成立，


= \sigma_\varepsilon^2 \sum_{j=0}^\infty \rho^{2j}=\frac{\sigma_\varepsilon^2}{1-\rho^2}
  • $|\rho| < 1$ 是保证级数收敛和方差有限的充要条件。

根据引理1，$\text{Var}[\lambda_1(A_t)] \approx 2\sigma^2 = \sigma_1^2$。为使模型与理论一致，可设：


\sigma_\varepsilon^2 = (1 - \rho^2) \cdot 2\sigma^2

此时：


\text{Var}[\tilde{z}_t] = 2\sigma^2 = \sigma_1^2

(3) 协方差仅依赖滞后 $k$

对 $k\ge0$，


  \gamma(k):=\operatorname{Cov}(\tilde z_t,\tilde z_{t-k})
            =\rho^{k}\sigma_{\tilde z}^{2},

仅含 k 而与 t 无关；于是


  \operatorname{Cov}(\lambda_1(A)_t,\lambda_1(A)_{t-k})=\gamma(k),

满足第三条。

(4) 平稳性的核心条件

  1. |ρ| < 1 是关键条件
    • 直观上：\rho 越小，当前特征值对过去的依赖越弱；
    • \rho=\pm1 会让方差发散，不可能稳态。
  2. 噪声独立性：\varepsilon_t 为白噪声，确保新信息与历史无关。

证明剩余特征值平稳：

1. 收缩操作（Deflation）的严格定义

设 A_t 的谱分解为：


A_t = \sum_{i=1}^N \lambda_i u_i u_i^\top,

其中 $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_N$，且 \{u_i\} 是标准正交基。

  • 第一次收缩：
    定义剩余矩阵 $A_{t,2} = A_t - \lambda_1 u_1 u_1^\top$，其性质为：

    • 特征值：$\lambda_2, \lambda_3, \dots, \lambda_N$（即移除 \lambda_1 后剩余特征值不变）。
    • 特征向量：u_2, \dots, u_N 保持不变（因 u_1 与其他特征向量正交）。

  • 第 k 次收缩：
    递归定义：

    
A_{t,k+1} = A_{t,k} - \lambda_k u_k u_k^\top,

    剩余矩阵 A_{t,k+1} 的特征值为 $\lambda_{k+1}, \dots, \lambda_N$。

每次收缩移除当前主成分，剩余矩阵的特征值是原始矩阵中未被移除的部分。

2. 剩余特征值的统计特性

目标：证明 \{\lambda_k(A_t)\}_{t \in \mathbb{Z}} 对 k \geq 2 也是弱平稳的。

(1) 均值恒定性

  • 剩余矩阵的期望：
    由线性性：

    
E[A_{t,k+1}] = E[A_t] - \sum_{i=1}^k E[\lambda_i u_i u_i^\top].

    若 A_t 的元素分布时不变，且 \lambda_i 和 u_i 的期望稳定（由主特征值的平稳性保证），则 E[A_{t,k+1}] 与 t 无关。

  • 特征值期望：
    对剩余矩阵 $A_{t,k+1}$，其主特征值 \lambda_{k+1}(A_t) 的期望近似为：

    
E[\lambda_{k+1}(A_t)] \approx (N-k-1)\mu + v + \frac{\sigma^2}{\mu} \equiv \mu_{k+1},

    其中 (N-k-1)\mu 是剩余非对角元素的贡献（假设每次收缩后非对角元素统计特性不变）。

(2) 方差恒定性

  • 剩余矩阵的方差：
    收缩操作通过正交投影移除 $\lambda_k u_k u_k^\top$，因此剩余矩阵 A_{t,k+1} 的元素方差仍为 $\sigma^2$（对角元素可能需调整）。
    由引理1的推广：

    
\text{Var}[\lambda_{k+1}(A_t)] \approx 2\sigma^2 \equiv \sigma_{k+1}^2.

  • 动态模型：
    假设去中心化序列 \tilde{z}_{k+1,t} = \lambda_{k+1}(A_t) - \mu_{k+1} 服从AR(1)：

    
\tilde{z}_{k+1,t} = \rho_{k+1} \tilde{z}_{k+1,t-1} + \varepsilon_{k+1,t}, \quad |\rho_{k+1}| < 1,

    稳态方差为：

    
\sigma_{\tilde{z}_{k+1}}^2 = \frac{\sigma_{\varepsilon_{k+1}}^2}{1-\rho_{k+1}^2} = \sigma_{k+1}^2.
(3) 协方差仅依赖滞后 $m$
  • 协方差函数： 
    
\gamma_{k+1}(m) = \text{Cov}(\tilde{z}_{k+1,t}, \tilde{z}_{k+1,t-m}) = \rho_{k+1}^{|m|} \sigma_{\tilde{z}_{k+1}}^2.
    仅依赖 $m$，与 t 无关。

3. 递推证明的完整性

  1. 归纳基础：
    k=1 时（主特征值），平稳性已证。

  2. 归纳假设：
    假设 \lambda_k(A_t) 的平稳性成立，即：

    • $E[\lambda_k(A_t)] = \mu_k$（常数），
    • $\text{Var}[\lambda_k(A_t)] = \sigma_k^2$（有限），
    • $\text{Cov}(\lambda_k(A_t), \lambda_k(A_{t-m})) = \gamma_k(m)$。

  3. 归纳步骤：

    • 通过收缩操作，\lambda_{k+1}(A_t) 成为 A_{t,k+1} 的主特征值。
    • 若 A_{t,k+1} 满足与 A_t 相同的统计假设（独立性、有界性、时不变性），则 \lambda_{k+1}(A_t) 的平稳性可类比主特征值的证明。

网络重构分析

假设网络中有 n 个节点，则矩阵 A(G) 的维度为 $n \times n$，预测得到特征值和特征向量后，可以根据矩阵谱分解理论进行逆向重构网络邻接矩阵，表示如下：


A(G) = \sum_{i=1}^n \hat{\lambda}_i \hat{x}_i \hat{x}_i^T

其中 \hat{\lambda}_i 和 \hat{x}_i 分别为通过预测得到矩阵 A(G) 的第 i 个特征值和对应特征向量。 然而预测值和真实值之间存在误差，直接进行矩阵重构会使得重构误差较大。 对于这个问题，文献提出一种 0/1 矩阵近似恢复算法。


a_{ij} = 
\begin{cases}
1, & \text{if}\ \lvert a_{ij} - 1 \rvert < 0.5 \\
0, & \text{else}
\end{cases}

只要我们的估计值与真实值之间差距小于 0.5，就能保证阈值处理以后准确地恢复原边信息。

文中提出网络特征值扰动与邻接矩阵扰动具有相同的规律

真实矩阵 A(G) 与预测矩阵 \hat{A}(G) 之间的差为


A(G) - \hat{A}(G) = \sum_{m=1}^n \Delta \lambda_m \hat{x}_m \hat{x}_m^T.

对于任意元素 (i, j) 上有


\left| \sum_{m=1}^n \Delta \lambda_m (\hat{x}_m \hat{x}_m^T)_{ij} \right| = |a_{ij} - \hat{a}_{ij}| < \frac{1}{2}

于一个归一化的特征向量 $\hat{x}_m$，其外积矩阵 \hat{x}_m \hat{x}_m^T 的元素理论上满足


|(\hat{x}_m \hat{x}_m^T)_{ij}| \leq 1.

经过分析推导可以得出发生特征扰动时，网络精准重构条件为：


\sum_{m=1}^n \Delta \lambda_m < \frac{1}{2}


\Delta {\lambda} < \frac{1}{2n}

0-1 矩阵能够精准重构的容忍上界与网络中的节点数量成反比，网络中节点数量越多，实现精准重构的要求也就越高。

如果在高层次（特征值滤波）的误差累积超过了一定阈值，就有可能在低层次（邻接矩阵元素）中出现翻转。公式推导了只要谱参数的误差之和不超过 0.5，就可以保证0-1矩阵的精确重构。

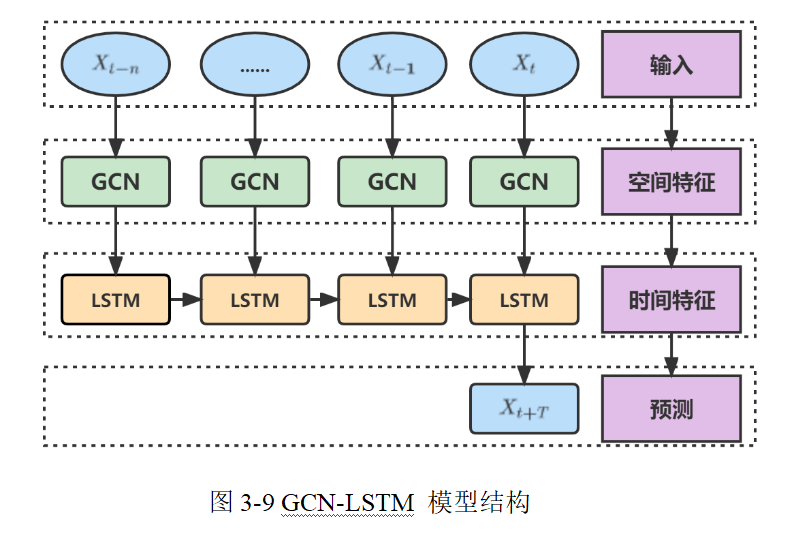
基于时空特征的节点位置预测

在本模型中，整个预测流程分为两大模块：

  • GCN 模块：主要用于从当前网络拓扑中提取每个节点的空间表示**。这里的输入主要包括：

    • 邻接矩阵 $A$：反映网络中节点之间的连通关系，维度为 $N \times N$，其中 N 表示节点数。(可通过第二章网络重构的方式获取)
    • 特征矩阵 $H^{(0)}$：一般是原始节点的属性信息，如历史位置数据，其维度为 $N \times d$，其中 d 是初始特征维度。

  • LSTM 模块：用于捕捉节点随时间变化的动态信息，对每个节点的历史运动轨迹进行序列建模，并预测未来时刻的坐标。
    其输入通常是经过 GCN 模块处理后，每个节点在一段时间内获得的时空融合特征序列，维度一般为 $N \times T \times d'$，其中 T 表示时间步数，d' 是经过 GCN 后的特征维度。

GCN 模块

输入

  • 邻接矩阵 $A$：维度 $N \times N$。在实际操作中，通常先加上自环形成

    
\hat{A} = A + I.

  • 特征矩阵 $H^{(0)}$：维度 $N \times d$，每一行对应一个节点的初始特征（例如历史采样的位置信息或其他描述）。

图卷积操作

常用的图卷积计算公式为：


H^{(l+1)} = \sigma \Bigl(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} H^{(l)} W^{(l)} \Bigr)

其中：

  • \tilde{A} = A + I 为加上自环后的邻接矩阵，
  • \tilde{D} 为 \tilde{A} 的度矩阵，定义为 $\tilde{D}{ii} = \sum{j}\tilde{A}_{ij}$；
  • H^{(l)} 表示第 l 层的节点特征，初始时 H^{(0)} 就是输入特征矩阵；
  • W^{(l)} 是第 l 层的权重矩阵，其维度通常为 $d_l \times d_{l+1}$（例如从 d 到 $d'$）；
  • \sigma(\cdot) 是非线性激活函数，例如 ReLU 或 tanh。

经过一层或多层图卷积后，可以得到最终的节点表示矩阵 $H^{(L)}$（或记为 $X$），维度为 $N \times d'$。
其中：

  • 每一行 x_i \in \mathbb{R}^{d'} 表示节点 i 的空间特征，这些特征综合反映了其在网络拓扑中的位置及与邻居的关系。

输出

  • GCN 输出：形状为 $N \times d'$；若将模型用于时序建模，则对于每个时间步，都可以得到这样一个节点特征表示。
  • 这里 d'>d 。1.高维嵌入不仅保留了绝对位置信息，还包括了网络拓扑信息。2.兼容下游LSTM任务需求。

LSTM 模块

输入数据构造

在时序预测中，对于每个节点，我们通常有一段历史数据序列。假设我们采集了最近 T 个时刻的数据，然后采用“滑动窗口”的方式，预测 $T+1$、 T+2...

  • 对于每个时刻 $t$，节点 i 的空间特征 x_i^{(t)} \in \mathbb{R}^{d'} 由 GCN 得到；

  • 将这些特征按照时间顺序排列，得到一个序列：

    
X_i = \bigl[ x_i^{(t-T+1)},\, x_i^{(t-T+2)},\, \dots,\, x_i^{(t)} \bigr] \quad \in \mathbb{R}^{T \times d'}.

对于整个网络来说，可以将数据看作一个三维张量，维度为 $(N, T, d')$。

LSTM 内部运作

LSTM 通过内部门控机制（遗忘门 $f_t$、输入门 i_t 和输出门 $o_t$）来更新其记忆状态 C_t 和隐藏状态 $h_t$。公式如下

  • 遗忘门：

    
f_t = \sigma(W_f [h_{t-1},\, x_t] + b_f)

  • 输入门和候选记忆：

    
i_t = \sigma(W_i [h_{t-1},\, x_t] + b_i) \quad,\quad \tilde{C}_t = \tanh(W_C [h_{t-1},\, x_t] + b_C)

  • 记忆更新：

    
C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t

  • 输出门和隐藏状态：

    
o_t = \sigma(W_o [h_{t-1},\, x_t] + b_o), \quad h_t = o_t \odot \tanh(C_t)

其中，x_t 在这里对应每个节点在时刻 t 的 GCN 输出特征；
[h_{t-1},\, x_t] 为连接后的向量；

LSTM 的隐藏状态 $h_i \in \mathbb{R}^{d'' \times 1}$（其中 d'' 为 LSTM 的隐藏单元数）捕捉了时间上的依赖信息。

输出与预测

最后，经过 LSTM 处理后，我们在最后一个时间步获得最终的隐藏状态 h_t 或使用整个序列的输出；接着通过一个全连接层（FC层）将隐藏状态映射到最终的预测输出。

  • 全连接层转换公式： 
    
\hat{y}_i = W_{\text{fc}} \cdot h_t + b_{\text{fc}}

其中，假设预测的是二维坐标（例如 x 和 y 坐标），$W_{\text{fc}} \in \mathbb{R}^{2 \times d''}$，输出 \hat{y}_i \in \mathbb{R}^2 表示节点 i 在未来某个时刻（或下一时刻）的预测坐标。

image-20250411142712730

若整个网络有 N 个节点，则最终预测结果的输出维度为 $N \times 2$（或 $N \times T' \times 2$，如果预测多个未来时刻）。

疑问

该论文可能有点问题，每个节点只能预测自身未来位置，无法获取全局位置信息。如果先LSTM后GCN可能可以！